В комментариях к моей статье про быстрое вычисление синуса был задан вопрос: "А чем не устроило разложение в ряд Тейлора?"
Краткий ответ таков: хоть приближение при помощи рядов Тейлора (точнее - рядами Маклорена) и даёт меньшую ошибку при том же количестве вычислений, но оно не позволяет разбить аргумент на произвольное количество интервалов и тем самым увеличить точность вычислений.
Теперь более подробно.
При приближении синуса (и не только) полиномами Чебышёва используют следующее выражение:
При этом коэффициенты А0, А1 и т.д. рассчитываются заранее для какого-то участка функции.
При помощи рядов Маклорена синус вычисляется по следующей формуле:
Для удобства вычислений можно вынести повторяющиеся фрагменты за скобки. Например, так:
или так:
Для примера найдём значения синуса на интервале от 0 до обоими методами, и постоим их графики вместе с графиком "настоящего" синуса.
Речь по прежнему идёт о скорости аппроксимации, поэтому оба метода будем сравнивать при примерно одинаковом количестве вычислений. То ест возьмём полином Чебышёва 2-й степени (с тремя членами), и с тем же количеством членов возьмём ряд Маклорена (получится степень 5):

График многочлена Чебышёва представляет собой фрагмент параболы, и пересекает график синуса в трёх точках, являющимися корнями многочлена.
График ряда Маклорена, начиная с левого края, почти совпадает с графиком синуса, и расхождение с ним начинается заметно на глаз только в правой трети диаграммы.
Графики ошибок аппроксимации выглядят так:
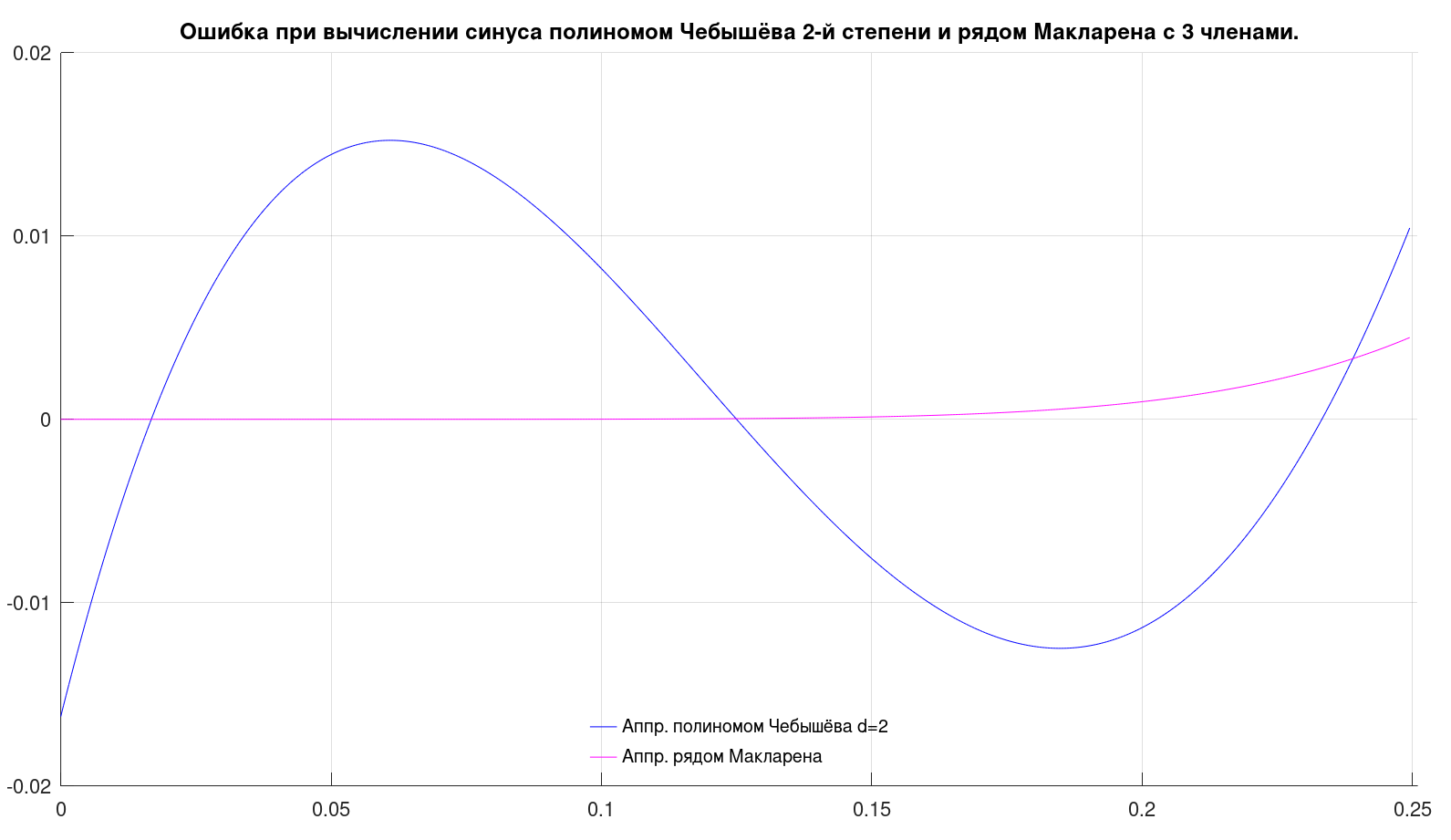
На них видно, что ошибка приближения полиномом Чебышёва в разы больше таковой у ряда Маклорена.
Теперь давайте посмотрим, как ошибки аппроксимации зависят от количества членов аппроксимирующей функции.
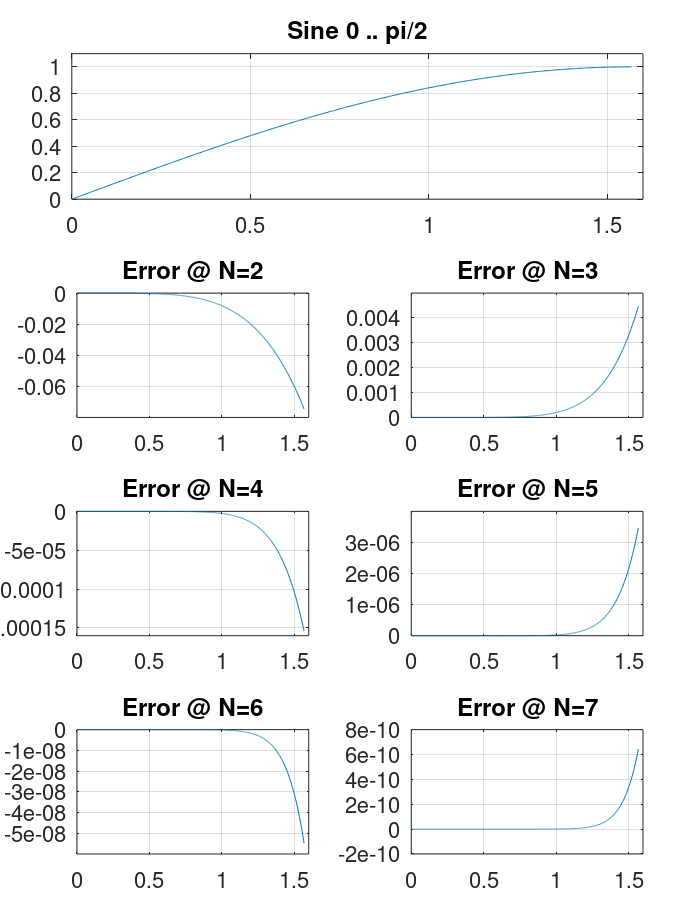
Графики ошибок аппроксимации рядами Маклорена разной длины выглядят так:
Графики ошибок аппроксимации полиномами Чебышёва имеют следующий вид:
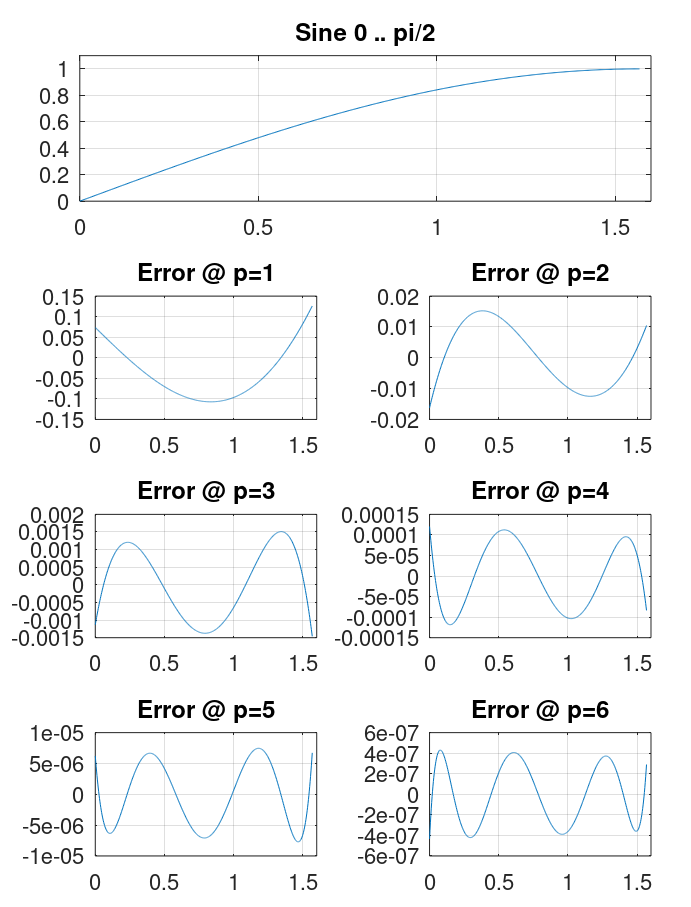
Графики ошибок выглядят по разному, но в обоих случаях величина ошибки падает с увеличением количества членов ряда. При этом точность полинома Чебышёва уже на порядки хуже таковой у рядов Маклорена.
На следующей диаграмме показана сравнительная точность аппроксимации обоими методами в зависимости от количества членов ряда (полинома). Точность выражена в "дробных битах", численно равных минус логарифму ошибки по основанию 2:

Вычисления производились с использованием 80-битных числе с плавающей запятой (тип long double). Результаты аппроксимации сравнивались со значением синуса, полученными стандартной функцией sinl() из библиотеки С компилятора gcc.
Приближение при помощи рядов Маклорена (зелёная линия) даёт большую точность по сравнению с полиномами Чебышёва (синяя линия). Точность не растёт выше какого-то предела, это связано с ошибками округления при вычислениях.
Однако для аппроксимации полиномами Чебышёва полный период (от 0 до можно разбить не на 4, как это делалось до сих пор, а, например, на 512 равных интервалов. На диаграмме этот случай представлен серой линией. Точность в 53.94 бита уже при 6 членах (полином 5-й степени) превышает таковую у ряда Маклорена в 51.62 бита при 10 членах ряда.
Вместо вывода. Пока что не существует идеального способа вычисления синуса, иначе не было такого их разнообразия. Подходящий способ выбирается как компромисс, исходя из заданных условий.
Комментарии (27)

northzen
09.10.2021 17:49+1Для быстрых вычислений синуса с произвольной точностью придуман CORDIC.

DrSmile
09.10.2021 18:12+1CORDIC — это семейство алгоритмов, работающих без использования операции умножения. Соответственно, никакого смысла его использовать при наличии железной реализации умножения нет, он гораздо медленней при той же точности.

northzen
09.10.2021 23:31+2Дык если автор тут бьется над аппроксимацией синуса (т.е. синуса у него в стандартных библиотеках не оказалось), то вполне может быть его ситуация, где HW часть достаточно бедна. Иначе зачем тут это? Берем готовую либу работы с длинными числами и вперед, там за автора уже все давно хорошо сделали.
Я кстати, не уверен, что Cordic будет медленнее, чем схемы, предложенные автором, для сравнимой точности.

DrSmile
09.10.2021 18:08+3На мой взгляд, абсолютно некорректное сравнение полиномов Чебышева в два раза более низкого порядка, чем у Маклорена. Если уж сравнивать, то ряды одинакового порядка, с одинаковой максимальной степенью x. Можно возразить, что нам повезло и половина членов обнулилась, так что все честно, однако никто не мешает аппроксимировать Чебышевым sin(√x) / √x и обнулить те же члены и там (не то, чтобы это имело смысл, ибо равномерная ошибка в этом случае неоптимальна, но, все равно, будет лучше Тейлора). Ну и еще в который раз скажу, что на практике не пользуются ни тем, ни другим, а просто делают L∞ оптимизацию коэффициентов подходящей формулы.

avitek Автор
09.10.2021 21:32делают L∞ оптимизацию коэффициентов подходящей формулы
С удовольствием бы почитал, как использовать это, например, в вычислениях на МК, с оценками точности и быстродействия. Поделитесь своим опытом?

DrSmile
09.10.2021 21:48+1В смысле, как использовать? Если это полином, то нет никакой разницы с точки зрения вычисления, находим ли мы коэффициенты Тейлором, Чебышевым или L∞ оптимизацией (за исключением случаев, когда случайно оказываются нулевые члены, как здесь). Оптимизация интересна тем, что работает не только для полиномов, позволяет задавать дополнительные условия (например, требование sin x = x для малых x) и задавать разные критерии ошибки (например, относительная или абсолютная). Однако выбор конкретной формулы — это уже больше искусство и математическая интуиция.

aamonster
09.10.2021 18:52+3Нравится мне – сравниваете полином Чебышёва 2-й степени с рядом Маклорена до 5-й. Будь у вас диапазон не от 0, а, скажем, от pi/4 до pi/2 (или не синус, а что-то посложнее) – вы бы так не сделали.
Ну или можете интерполировать (sin x)/x как функцию от x² – тогда полином Чебышёва с 3 членами как раз будет по тем же степеням, что Маклорена: и сравнение на равных, и сложность вычисления.
Ну и вишенка на торте: exp(-1/x²) попробуйте аппроксимировать.

avitek Автор
10.10.2021 16:40Нравится мне – сравниваете полином Чебышёва 2-й степени с рядом Маклорена до 5-й.
Речь идёт о соизмеримых количествах вычислений в свете быстродействия.
Я поправил статью, что бы это было очевидно. Если старый текст ввёл Вас в заблуждение - мой косяк, прошу извинить.
aamonster
10.10.2021 18:35+1Ну так ряд Тейлора можете считать в тех же диапазонах, в которых делаете интерполяцию полиномами Чебышёва. При этом вам уже не удастся "схалявить" благодаря нечётной функции, и сравнение будет на равных. Вангую, что при этом решение с п.Ч. окажется точнее (и именно на это интересно посмотреть)
Другой подход – привести аргумент к диапазону в окрестности нуля, вычислить синус и косинус, привести обратно (понадобится таблица синусов и косинусов для середин диапазонов). Как раз получится, что вам придётся, скажем, для 7 степени посчитать 8 членов – 4 в косинусе и 4 в синусе. Опять сравнение получится на равных. Кстати, в диапазоне (-a,a) и при интерполяции полиномами Чебышёва в синус войдут только нечётные степени x, а в косинус – только чётной. Т.е. сможете сравнить три подхода, приближающих полиномами одной и той же степени: интерполяцию п.Ч. "на месте" и два варианта с приведением аргумента.
ЗЫ: и попробуйте, правда, ряд Маклорена для приведённой мной функции. Он очень простой, а результаты интересные :-)

ZyXI
10.10.2021 00:40+1Вычисления производились с использованием 80-битных числе с плавающей запятой (тип long double). Результаты аппроксимации сравнивались со значением синуса, полученными стандартной функцией sinl() из библиотеки С компилятора gcc.
Мне вот интересно, почему ещё никто не прицепился к этой части? В стандарте по поводу этой функции сказано только, что она вычисляет синус, никаких требований к точности не предъявляется. А функция ведь будет сама использовать какую‐то аппроксимацию, а не вызывать особую компьютерную магию, чтобы в выходном регистре появилось настолько точное значение синуса, насколько это позволяет формат long double. Так что не хватает исследования точности sinl.
И, кстати, при чём тут gcc? sinl лежит в libm, а libm согласно моему пакетному менеджеру, относится к пакету glibc.

AVI-crak
10.10.2021 06:57+2/// sin input is radian +-2pi, output 1.0:-1.0. /// min |x|=2.62879913375e-23 error 2L float sin_f(float value_rad) { float ret, rev, res; // if (abs_f(value_rad) < 2.62879913375e-23f ) return value_rad; ret = value_rad; if (ret < (PI/(-2.0f))) ret += Pi2; if (ret > (Pi+ PI/2.0f)) ret -= Pi2; else if (ret > (PI/2.0f)) ret = PI - ret; rev = ret * ret; res = rev * -2.50516549727e-08f; res += 2.75573984254e-06f; res *= rev; res += -0.000198412570171f; res *= rev; res += 0.00833333469927f; res *= rev; res += -0.166666656733f; res *= rev; res *= ret; res += ret; return res; };Учитывалась ошибка округления констант, общая ошибка ограниченного ряда, и ошибка приближения. Даа, это три разных типы ошибки. В сумме получилось 21 бита точности мантисы, что чуть выше значений вашего графика для Трейлера. Накопительное значение ошибки 0.1561978 младшего бита матиссы. Почти все ошибки 1L, в двойку ещё нужно попасть.
До значений +1, -1 - функция доходит.

Refridgerator
10.10.2021 08:22+6В моих измерениях аналогичного характера результат получился вполне однозначным и при одной и той же степени vyjujxktys Чебышева давали на 2 десятичных знака больше, чем Тейлора. И это вполне логично — ведь у Чебышева ошибка равномерно распределена по всему интервалу. У Тейлора же вся точность сосредоточена около нуля и на некотором этапе вычислений просто перестаёт иметь смысл.
На практике для вычисления синуса/косинуса с 30-ю знаками после запятой я использую 4 таблицы по 64 значения, и на сам ряд остаётся интервал от 0 до pi/16384 (0.000191748), для вычисления которого достаточно многочлена 5-ой степени.
avitek Автор
10.10.2021 16:29.... Чебышева давали на 2 десятичных знака больше, чем Тейлора.
Имеется в виду "точность на 2 десятичных знака больше"? Если да, то наверное Вы проверяли в диапазоне как минимум до 180°.
Я же проверял только первый квадрант, т.к. в силу симметрии функции этого достаточно.
Refridgerator
10.10.2021 16:52+1Ну вот например в диапазоне до pi/4 у меня так получилось:
скриншот

avitek Автор
10.10.2021 17:02Всё верно, спасибо. Я пропустил, что Вас в первом комментарии написано "при одной и той же степени", для полинома Чебышёва при этом нужно сделать почти в 2 раза больше вычислений. Я же сравнивал, исходя из одинаковых вычислительных затрат, степени при этом получались разные. Статью я поправил соответственно...

Refridgerator
10.10.2021 17:06+1А почему вычислений-то больше? Там же только коэффициенты разные.

avitek Автор
10.10.2021 20:51Связано с тем, что функция аппроксимировалась для интервала от 0 до 90°. Но по хорошему надо было делать симметрично, как указано в соседнем комментарии.

Refridgerator
11.10.2021 05:28Можно было и разложение в ряд взять в точке pi/4, а не в нуле — там же погрешность в обе стороны растёт.

aamonster
10.10.2021 18:44+2Кстати, тут вы ошиблись. От -a до a для расчёта через п.Ч. все коэффициенты при чётных степенях x тоже обратятся в 0, та же сложность.


lorc
А если взять все же ряд Тейлора и посчитать это коэффициенты для тех же 512 интервалов? Точнее, для средних точек интервалов, но идею вы поняли, наверное.
Sdima1357
Ну к третьей статье, когда автор все же удосужится прочитать школьный учебник за 9-й класс, мы может и дождемся результата разложения в ряд Тейлора вокруг окрестностей точек.
Добавил. Извиняюсь, соврал. Жена- учительница математики. Говорит, что в школе разложение в окрестности точки в ряд Тейлора - не проходят. Память подвела. Или учитель подвёл, рассказал лишнее.
vesper-bot
У нас в физматшколе в математическом классе ряды были еле-еле в 11м классе, и то во внеклассной программе. Тем более в 9м.
Sdima1357
Когда я учился было только 10 классов. И в моей школе разложение в ряд Тейлора проходили в 9 классе. (Сейчес она Московская школа № 1514. Была математическая школа № 52 при ВЦ АН СССР). Но речь не об этом. Я ошибся, думал что проходят во всех школах.
mentin
У ряда Тейлора на всех интервалах кроме нулевого появятся ненулевые коэффициенты перед чётными степенями - то есть Чебышев и Тейлор будут в одинаковых условиях (в статье порядок Тейлора в два раза больше порядка Чебышева). Подозреваю, разница в точности пропадет, а может и будет в пользу Чебышева.