При моделировании данных методом наименьших квадратов, кривая обычно не проходит через точки измерений (рис. 1).
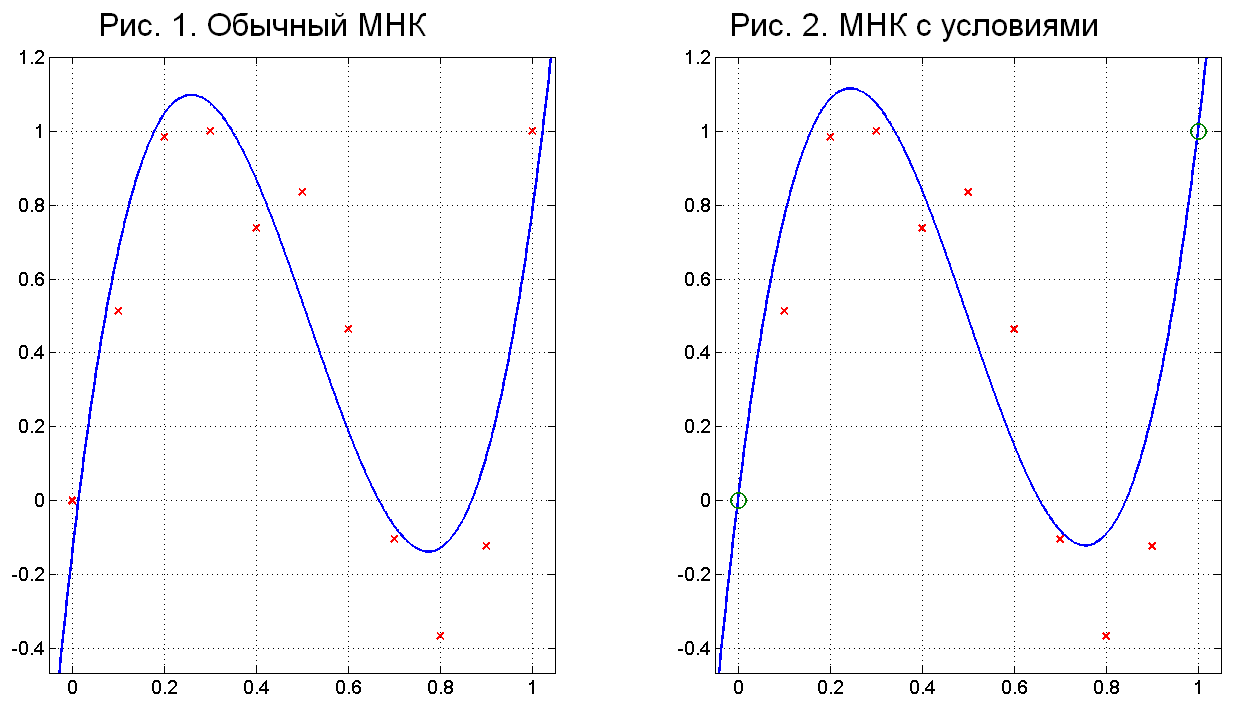
Что, если нужно, чтобы эта кривая точно проходила через одну или несколько особо выделенных точек (рис. 2 - показаны зелёными кружочками)?
Тогда читаем дальше.
1. Мотивация
Рассмотрим обычную задачу приближения многочленом и посмотрим, чего нам в ней не хватает.
Дано N точек на плоскости (xi,yi) - значения неизвестной функции f(x). Требуется найти многочлен p(x) степени M (M<N), наилучшим образом приближающий эту функцию.
Часто полагают, что "наилучшим" является многочлен, сумма квадратов отклоненийкоторого от заданных точек минимальна:
В таком виде задача решается широко известным методом наименьших квадратов (МНК).
При M<N-1 многочлен p(x), вообще говоря, не проходит через все заданные точки (xi, yi) (рис. 1). Более того, часто оказывается, что он не проходит ни через одну из них.
Само по себе это не плохо. Обычно данные, по которым строится приближение, содержат погрешности измерений. Даже лучше, что многочлен не проходит через все точки, так как при этом ошибки измерений сглаживаются.
Однако бывает, что о моделируемой зависимости имеются дополнительные сведения. Например, моделируется отклик датчика на некую величину. И из физических соображений ясно, что этот отклик строго равен нулю при равенстве нулю величины. При моделировании характеристики такого датчика может оказаться, что аппроксимирующий многочлен не пройдет через нуль. В результате модель даст большую погрешность в районе нуля.
В такой ситуации хотелось бы найти многочлен со следующими свойствами:
Точно проходит через нуль
Имеет наименьшую сумму квадратов отклонений от остальных измеренных значений
В статье описывается метод, позволяющий найти такой многочлен. Более того, можно потребовать точного прохождения многочлена не через одну, а несколько выделенных точек.
2. Решение
2.1. Взвешенный метод наименьших квадратов
Как ингредиент нам потребуется взвешенный метод наименьших квадратов, который минимизирует сумму квадратов отклонений с весовыми коэффициентами в каждой точке:
Где wi - весовые коэффициенты. Обычно взвешенный МНК используется для учета погрешностей измерений в каждой точке, поэтому в литературе часто используют не понятие веса, а обратную дисперсию σ2 погрешностей:
Взвешенный МНК хорошо описан в книге [1], гл. 15.1, 15.4.
2.2. Точное прохождение через нуль
Начнём с простого случая: потребуем точного прохождения многочлена p(x) через нуль.
Для этого найдём многочлен q(x) степени M-1 по модифицированным точкам (xi, yi/xi) с помощью взвешеннго МНК, выбрав в качестве весов wi=xi2; и умножим его на x. Тогда:
Он будет иметь степень M и точно проходить через нуль.
Рассмотрим сумму квадратов его отклонений от остальных точек (xi, yi):
Но именно эта величина и минимизируется взвешенным МНК по модифицированным точкам. Поэтому многочлен p(x) будет соответствовать и второму условию задачи - иметь наименьшую сумму квадратов отклонений от (xi, yi).
2.3. Точное прохождение через одну произвольную точку
Усложним задачу и потребуем точного прохождения многочлена p(x) через одну произвольно заданную точку (ξ,η).
Путём замены переменных u=x-ξ, v=y-η, задача сводится к рассмотренной выше. Находим коэффициенты многочлена p0(u), проходящего через нуль и имеющего наименьшую сумму квадратов отклонений p0(ui)-vi. Далее переходим к исходным переменным:
Для нахождения коэффициентов p(x) можно провести алгебраические манипуляции с коэффициентами p0(x-ξ), но есть и более простой на практике способ. Поскольку у нас в программе уже имеется реализация обычного МНК, то можно просто вычислить значения p(x) по формуле (1) в каких-нибудь M+1 или более точках, и применить к этим значениям обычный МНК, задав степень многочлена M. Тем самым и будут найдены коэффициенты p(x).
2.4. Точное прохождение через несколько точек
И, наконец, самый общий случай - потребуем точного прохождения многочлена p(x) через K заданных точек (ξi, ηi). Следует выбирать K ≤ M, в противном случае задача вырождается в интерполяцию.
Переходя к решению, введем многочлен z(x) степени K:
Он имеет нули в точках ξ1, ξ2, ... ξK.
Также введем интерполяционный многочлен Лагранжа L(x) степени K-1, проходящий через точки (ξi, ηi) [1], гл. 3.1.
Используем взвешенный МНК для нахождения многочлена q(x) степени M-K по модифицированным точкам: (xi, (yi-L(xi))/z(xi)) с весовыми коэффициентами wi=z(xi)2. Получим коэффициенты {aj} для q(x), которые минимизируют сумму:
Теперь составим многочлен p(x) как:
Докажем, что p(x) является решением задачи.
Прохождение через точки (ξi, ηi) обеспечивается тем, что z(ξi)=0, обращая в нуль первое слагаемое. Второе слагаемое в этих же точках, L(x), проходит через (ξi, ηi) по построению.
Степень p(x) равна M, так как степень произведения многочленов q(x) и z(x) равна сумме степеней множителей. В данном случае M-K+K=M. Сумма же многочленов имеет степень старшего из слагаемых. Степень L(x) равна K-1, что по условию меньше M.
Запишем сумму квадратов отклонений в точках (xi, yi):
Но это совпадает с величиной (2), которая минимизировалась при нахождении коэффициентов q(x). Следовательно, p(xi) имеет наименьшую сумму квадратов отклонений от yi. Что и требовалось доказать.
Для нахождения коэффициентов p(x) можно провести алгебраические манипуляции с q(x), z(x) и L(x), но это еще сложнее, чем в разделе 2.3. выше. Так что здесь тоже рекомендуется вычислить значения p(x) в M+1 или более точках по формуле (3) и применить к ним обычный МНК.
3. Цена вопроса и рекомендации к применению
За всё в этой жизни приходится платить. Наложение условия точного прохождения через точки (ξi, ηi) на многочлен p(x) приводит к тому, что сумма квадратов его отклонений от остальных точек (xi, yi) оказывается, вообще говоря, выше, чем без наложения условий.
Фактически, мы решили задачу условной оптимизации суммы квадратов отклонений p(xi)-yi. Как и в других задачах условной оптимизации, достигаемое значение целевой функции получается хуже, чем при оптимизации безусловной. В противном случае и безусловная оптимизация дала бы тот же результат.
Когда же следует применять описанный метод? Тогда, когда о моделируемой зависимости имеются "железобетонные" сведения, что она должна проходить через точки (ξi, ηi) независимо от экспериментальных данных (xi, yi).
В моей практике был один такой случай. Моделировалась нелинейная характеристика датчика. Истинный вид функциональной зависимости был неизвестен. Оставалось только использовать многочлены в попытке хоть как-то компенсировать нелинейность. Но многочлены плохо описывали характеристику около нуля. Полученные обычным МНК, они стремились не проходить через нуль. Тем не менее, из физических соображений было ясно, что характеристика датчика должна проходить через нуль. Вот тогда наложение условия и пригодилось. Его применение позволило улучшить компенсацию нелинейности в окрестностях нуля и уменьшить относительную погрешность прибора в целом.
4. Пример с конкретными числами
Этот пример был использован для построения графиков, приведенных на рис. 1 и рис. 2.
В качестве "истинной зависимости" был взят следующий многочлен:
Где T3(x) - многочлен Чебышева третьего порядка. Модификации применены к нему для того, чтобы отобразить интересный участок графика в диапазон x,y ∈ [0; 1]. p1(x) проходит через точки (0,0) и (1,1). Разложение его по степеням x выглядит так:
В качестве данных для метода наименьших квадратов (обычного и условного) взяты значения p1(x) в 11 равноотстоящих точках между 0 и 1 с шагом в 0,1. К значениям многочлена была добавлена нормально распределенная "ошибка измерений" δi с дисперсией σ2=0,04. В точках x1=0 и x11=1 ошибка не добавлялась. По случайным числам карты легли следующим образом:
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
xi |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
δi |
0 |
-0,1617 |
0,0162 |
0,0294 |
-0,0458 |
0,3358 |
0,2476 |
-0,1325 |
-0,3986 |
-0,4477 |
0 |
Приближение обычным МНК по заданным точкам при M=3 дало следующие коэффициенты:
График p2(x) изображен на рис. 1. Достигнутая сумма квадратов отклонений p2(x)-yi составила 0,4019.
Для испытания описываемого в разд. 2.4. метода было поставлено условие точного прохождения многочлена через точки (0,0) и (1,1), а в остальных точках - минимизация суммы квадратов отклонений. В результате был получен следующий многочлен:
Его график изображен на рис. 2. Достигнутая сумма квадратов отклонений p3(x)-yi составила 0,5046.
Из приведенного примера можно сделать вывод, что теоретические выкладки подтвердились. Был найден многочлен p3(x), приближающий "экспериментальные данные" и проходящий через точки (0,0) и (1,1). Как предсказывалось в разд. 3, сумма квадратов его отклонений от точек (xi, yi) оказалась больше, чем у многочлена p2(x), найденного обычным МНК. Тем не менее, эта жертва может быть оправданной, если прохождение p3(x) через точки (0,0) и (1,1) важнее.
Что касается совпадения коэффициентов многочленов p2(x) и p3(x) с коэффициентами "истинного" многочлена p1(x) - то на паре-тройке наборов тестовых данных особой закономерности не выявилось. Наверное, есть смысл провести тест Монте-Карло и сравнить распределения коэффициентов p2(x) и p3(x) на большой выборке.
Заключение
В статье был получено обобщение метода наименьших квадратов, позволяющее налагать на многочлен условие прохождения через заданные точки.
Задачу удалось свести к применению взвешенного метода наименьших квадратов и интерполяции многочленом Лагранжа. Поскольку обе операции сводятся к решению системы линейных уравнений, то и описанный в статье метод сохраняет эту (невысокую) вычислительную сложность. Точное решение можно получить за конечное число действий и (при должной усидчивости или использовании систем компьютерной алгебры) выразить аналитически.
Возможны обобщения метода для задач приближения не только многочленами, а и другими функциями. Но эта тема обширна и может быть рассмотрена только в отдельных публикациях.
Литература
[1] William H. Press и др. "Numerical Recipes in C++: The Art of Scientific Computing", Second Edition. Cambridge University Press, ISBN 0-521-75033-4
Комментарии (30)

Andy_U
18.10.2021 23:57Стандартная задача на поиск условного минимума. Обычно решается применением метода множителей Лагранжа...
MichaelBorisov Автор
19.10.2021 00:59Я тоже думал применить к данной задаче метод множителей Лагранжа, но есть подозрение, что это приведет к нелинейным уравнениям, которые потом будет трудно решать. Детально не проверял.

Andy_U
19.10.2021 01:19+1Вы к квадратичной форме добавите столько линейных условий (условие, что полином в данной точке равен фиксированному значению - линейное уравнение для коэффициентов), сколько точек у вас зафиксировано. Компоненты градиента модифицированной целевой функции - останутся линейными функциями от коэффициентов полинома и множителей Лагранжа.
MichaelBorisov Автор
19.10.2021 01:29+1Спасибо, обнадёжили! Надо будет попробовать. Если уравнения и правда останутся линейными — то с помощью метода множителей Лагранжа можно будет эффективно решать и более общую задачу линейной аппроксимации произвольными функциями с условием прохождения через точки. Достойно отдельной статьи!

teleport_future
19.10.2021 01:00Все это интересно, но с практической точки зрения не понятно как решить вашу задачу. Раньше как то проще все делалось - был справочник по расчетам на микрокалькуляторах, где приводились готовые алгоритмы и совсем немного теории, а у вас же все наоборот.
MichaelBorisov Автор
19.10.2021 01:02+1Эта статья рассчитана на подготовленного читателя, который уже знает (в университете это изучается), что такое метод наименьших квадратов, и умеет его применять (обычно с помощью компьютера — есть соответствующие программные пакеты и библиотеки).
В описаниях численных методов в литературе и научной периодике обычно приводится только теория и формулы. Опять же, подготовленному читателю именно это и нужно. Он сам потом сможет реализовать всё это в виде программы для компьютера.

Refridgerator
19.10.2021 06:07+1Интересная задача, тоже ей занимался. Но я пошёл другим путём.
1) для условия прохождения через заданные точки (а также значения производных в некоторых из этих точек) просто составлялась система уравнений. После её решения оставались несколько свободных коэффициентов, которые и можно было было подбирать.
2) Метод наименьших квадратов — не наилучший, а на наилёгкий, потому как легко математически описывается через производную интеграла. Наилучший — это минимизация максимального отклонения, но математически описать такое отклонение довольно проблематично (в общем случае, в частном случае многочлены Чебышева могут помочь). Однако некоторые инструменты численной аппроксимации позволяют к нему приблизиться.
3) аппроксимация многочленом — тоже не наилучший, а наилёгкий способ, имеющий хорошо известные проблемы в виде неожиданных пульсаций там, где их быть не должно (особенно если нам заранее известен вид функций), и особенно при больших степенях. Отношение двух многочленов обычно даёт намного лучшую сходимость — правда, имеет свои проблемы в виде возможных полюсов (когда знаменатель обращается в ноль).
Naf2000
19.10.2021 07:24+5Наилучший — это минимизация максимального отклонения
Чтобы говорить категориям лучший/худший надо ввести соответствующие определения. Обычно критерием является соответствующая метрика в пространстве функций. Так вот от её выбора может быть лучшим как метод наименьших квадратов, так и что-то иное.
MichaelBorisov Автор
20.10.2021 00:39Благодарю за внимание к статье.
2) Метод наименьших квадратов — не наилучший, а на наилёгкий
Насчет «наилучшего» хорошо ответил Naf2000 выше. Наилёгкий — это верно. И это важное свойство, которым можно и нужно пользоваться. Чтобы ставить и решать задачи, которые трудно или невозможно решать при других критериях оптимальности, таких как упомянутый вами минимакс.
Я тоже люблю минимакс-аппроксимацию и использую при случае. Алгоритм Ремеза — наше всё!аппроксимация многочленом — тоже не наилучший, а наилёгкий способ
Безусловно, это наилёгкий способ. Но иногда он является и наилучшим — если истинная зависимость, которую моделируют по экспериментальным данным, является многочленом. Кроме того, многие другие случаи приближения сводятся к многочленам.хорошо известные проблемы в виде неожиданных пульсаций там, где их быть не должно (особенно если нам заранее известен вид функций), и особенно при больших степенях
Каждому инструменту — своё применение. Конечно, большие степени для МНК обычно не применяются (а если применяются — то это классический Overfitting). Проблема пульсаций больше характерна не для МНК с многочленами, а для интерполяции многочленом Лагранжа. Опять же, надо владеть арсеналом разных методов и применять в конкретной ситуации наиболее подходящий. «Серебряной пули», универсального метода на все случаи жизни, не существует. Я увлекался минимакс-фильтрами для обработки сигналов, пока жизнь не подкинула такие сигналы, для которых этот метод плохо подходит.
Refridgerator
20.10.2021 06:07Большие степени для МНК обычно не применяются
Я применял — для аппроксимации нарисованной мышкой АЧХ. Но мой комментарий был скорее о том, что классический подход хорошо работает на небольшом наборе данных и степени не выше 5. А как только требуется увеличить точность и количество исходных данных — сюрприз. Конечно, решение МНК через матрицы частично решают эту проблему, но это уже совсем другой уровень сложности.Я увлекался минимакс-фильтрами для обработки сигналов, пока жизнь не подкинула такие сигналы, для которых этот метод плохо подходит.
Какие, если не секрет? Проблему фильтров я решил поиском вида функции (в частотной области), которая даёт максимально быстрое затухание импульсной характеристики (примерно e-x2/x).MichaelBorisov Автор
20.10.2021 20:46Я применял — для аппроксимации нарисованной мышкой АЧХ.
Можно подробнее? Для чего аппроксимировалась АЧХ? Синтез фильтров?классический подход хорошо работает на небольшом наборе данных и степени не выше 5
Я бы не был так категоричен. Все зависит от истинной зависимости, имеющейся в данных. Если она полиномиальная и высокой степени — то можно применять МНК без ограничений. Я часто использую МНК для нахождения коэффициентов многочленов. То есть вычисляю значения многочленов (напр., по формуле Лагранжа) в большом числе точек, а потом применяю на этих данных МНК. Количество точек и степень многочлена могут достигать при этом больших величин. Кто-то скажет, что это стрельба из пушки по воробьям, но я обнаружил, что такой подход меньше подвержен погрешностям округления, чем, например, алгебраические преобразования коэффициентов. И код специализированный писать не надо.Конечно, решение МНК через матрицы частично решают эту проблему
Что значит «через матрицы»? Бывает разве без матриц?Какие, если не секрет?
Это были сигналы с датчиков. В них в известные моменты времени присутствовала импульсная помеха большой амплитуды. Фильтры, естественно, размазывали эту помеху, но особенно неприятно было поведение линейно-фазовых фильтров, так как они размазывали помеху и вперед, и назад. Решил применять только каузальные фильтры, чтобы хотя бы участок сигнала перед помехой не был искажен.
Также оказались важны следующие свойства, нехарактерные для высококачественных аудио-фильтров: 1) сохранение амплитуды (т.е. прохождение интерполяционной кривой через исходные точки); 2) отсутствие колебаний импульсной характеристики.Проблему фильтров я решил поиском вида функции (в частотной области), которая даёт максимально быстрое затухание импульсной характеристики
Почему именно импульсной? Это же наверняка приводило к ухудшению приближения частотной характеристики. Какие у вас были фильтры, рекурсивные? Уравнения Юла-Уокера не пробовали использовать? В матлабе есть функция "yulewalk" — для нахождения коэффициентов рекурсивных фильтров по АЧХ.
Refridgerator
21.10.2021 06:25+1Можно подробнее? Для чего аппроксимировалась АЧХ?
1) Есть класс эффектов под названием «свёрточный ревербератор», у которых эффект реверберации достигается свёрткой сигнала с импульсной характеристикой помещения. У них есть подкласс «эмулятор гитарного кабинета» с аналогичным принципом действия. Импульсные характеристики для них записываются на микрофон откликом на единичный импульс. Пользователь перебирает эти импульсы и выбирает с наиболее подходящим звучанием.
Но перебирать сотни и тысячи импульсных характеристик — сомнительное удовольствие особенно с учётом того, что импульсы для одного и того же кабинета сильно разнятся в зависимости от положения микрофона при записи. Было бы удобнее контролировать звучание более управляемым способом.
Меня также интересовала эмуляция звучания телевизора для эмулятора Zx Spectrum — а для телевизоров импульсных характеристик никто не снимал.
2) Другая задача — это сглаживание АЧХ, также полученной через микрофон, для коррекции динамиков/колонок/помещения.
3) ещё одна задача — для спектральной интерполяции, например, в случае уже упомянутых вами импульсных выбросов (для винил-рипов). Импульс можно детектировать нелинейными методами, но его недостаточно просто удалить — нужно ещё чем-то заполнить освободившееся пространство.Бывает разве без матриц?
У меня нет специального образования, с математикой в школе было всё плохо (а с матрицами — особенно), не было доступа к литературе, доступ к интернету был пределом мечтаний, а про МНК я узнал на кухне за кружкой чая от человека, который тоже имел о нём весьма поверхностное уравнение. Поэтому я просто решил решил в Mathcad-е уравнения и получил формулы для коэффициентов в явном виде, непосредственно через координаты точек. Для больших степеней использовал базис a*cos(k x)+b*sin(k x) итеративным образом, последовательно увеличивая k.
МНК также можно посчитать чисто аналитически, для непрерывной функции, а не на дискретных значениях.Почему именно импульсной? Это же наверняка приводило к ухудшению приближения частотной характеристики. Какие у вас были фильтры, рекурсивные?
FIR-фильтры с линейной фазой и наоборот, чисто фазовые фильтры с линейной АЧХ (например, преобразование Гильберта или ЛЧМ-подобный сигнал).
Проблема в том, что при получении коэффициентов фильтра через обратное преобразование Фурье они довольно медленно затухают (классический пример — sinc для brickwall фильтра) и их ограничивают умножением на оконную функцию, что приводит к искажению АЧХ. В простых случаях можно просчитать что получится, в сложных — уже сложнее, фазовые фильтры с линейной АЧХ таким образом вообще сделать не получится. Я искал способ, чтобы после обратного преобразования Фурье импульсная характеристика естественном образом уходила в ноль (в рамках погрешности вычислений). Это избавляет и от мучительных размышлений, какую именно оконную функцию выбрать, и позволяет определить необходимое количество коэффициентов для каждого конкретного фильтра.MichaelBorisov Автор
22.10.2021 00:19Спасибо за ответы. Значит, вы со звуком много работали! Мне методы обработки звука тоже интересны.
эмуляция звучания телевизора для эмулятора Zx Spectrum
Ого, необычный проект! Вы участвуете в создании эмуляторов ZX Spectrum?недостаточно просто удалить — нужно ещё чем-то заполнить освободившееся пространство
Линейное предсказание не пробовали? Я пробовал, результаты понравились.про МНК я узнал на кухне за кружкой чая
«Классический» МНК сводится к решению системы линейных уравнений, а это и есть матричная алгебра в чистом виде. Можно, конечно, решать и без привлечения понятия матриц, но все равно они там незримо присутствуют.МНК также можно посчитать… для непрерывной функции
Да, можно. Для синтеза FIR-фильтров есть такой метод.
Похоже, по синтезу фильтров у нас с вами общие интересы, но, наверно, общение на тему фильтров лучше будет перенести в личку или на более подходящий форум, а то тут несколько оффтопик. Пишите!
Refridgerator
22.10.2021 07:15Вы участвуете в создании эмуляторов ZX Spectrum?
Нет, я просто брал готовые проекты с открытым исходным кодом и внедрял туда свои фильтры для проверки концепции.примерК сожалению, они все довольно ресурсоёмкие и для полноценного использования нужна оптимизация и куча дополнительного времени.
Линейное предсказание не пробовали?
Идея было в том, чтобы в случае «разорванной» синусоиды произвольной частоты восстанавливать потерянный фрагмент как можно ближе к оригиналу.типа такогоНе уверен, что линейное предсказаниие так может.

Refridgerator
11.11.2021 06:15Проблема пульсаций больше характерна не для МНК с многочленами, а для интерполяции многочленом Лагранжа
Контр-пример с многочленом 10-ой степени:
И пульсации хороши видно, и увеличение степени многочлена проблемы не решит.
А вот аппроксимация рациональным многочленом, той же степени и с тем же количеством коэффициентов:
И по поводу выбора подходящего инструмента: я не видел ни одной статьи на хабре о рациональной аппроксимации, зато статей о МНК миллиард. Так что нет никакого выбора.UPD: вариант с шумом

Refridgerator
11.11.2021 08:00UPD: соврал, степень рационального многочлена здесь в 2 раза меньше — числителя 5, знаменателя 4.

aamonster
19.10.2021 07:56+2Как-то всё сложно...
Метод наименьших квадратов же не прибит гвоздями к базису 1, x², x³,.... Это раз.
И два – можно построить через фиксированные точки кривую (например, многочлен минимальной степени). Получается, что нам останется аппроксимировать отклонение точек от этой кривой (со знаком). Т.е. функцию с несколькими фиксированными корнями. Берём базис из функций с такими же корнями (надо подсказывать, как он получается из многочленов?) и прогоняем стандартный метод наименьших квадратов. Задача решена.

Andy_U
19.10.2021 09:55Как вы перешли от полинома, проходящего через фиксированные точки (x[i]!=0, y[i]!=0), к полиному с фиксированными корнями?

aamonster
19.10.2021 12:08+3Вычитанием, конечно.
Допустим, у нас есть три фиксированные точки (X0,Y0), (X1,Y1), (X2,Y2) и десять точек (x_i,y_i) для приближения. По трём фиксированным точкам строим полином (параболу в данном случае) P0(x) = ax^2+bx+c (интерполяционный полином Лагранжа).
Дальше для остальных точек (x_i, y_i) считаем y'_i = y_i - P0(x_i) и приближаем их МНК по базису
1*(x-X0)*(x-X1)*(x-X2)
x*(x-X0)*(x-X1)*(x-X2)
x^2*(x-X0)*(x-X1)*(x-X2)
...
(столько, сколько надо)
Получили полином P1(x) такой, что P1(X0)=P1(X1)=P1(X2)=0 и приближающий наши разности.
Наш ответ, очевидно, P(x) = P0(x) + P1(x).
P0(X_i)=Y_i, P1(X_i)=0 - с фиксированными точками всё хорошо
y_i -P(x_i) = y'_i + P0(x_i) - P(x_i) = y'_i - P1(x_i) - как раз то, что мы старались улучшить МНК, опять всё хорошо.
Andy_U
19.10.2021 12:29Спасибо, теперь понятно стало.
MichaelBorisov Автор
19.10.2021 18:41Именно этот метод, с несущественным отличием, и был реализован в статье. Раздел 2.4.
MichaelBorisov Автор
19.10.2021 18:39Вы фактически пересказали основное содержание статьи (разд. 2.4.). Красиво, однако! А мне надо ещё много учиться лаконичности.

aamonster
19.10.2021 18:49+1Ну, я по анекдоту про математика пересказывал:
Дано: Дрова, спички, пустой чайник, река.
Задача: Вскипятить воду.
Физик - Взять чайник, пойти наполнить водой, разжечь костер, укрепить чайник, ждать.
Математик - то же самое.Дано: горящие Дрова, спички, полный чайник, река.
Задача: Вскипятить воду.
Физик - укрепить чайник, ждать.
Математик - затушить огонь из чайника. Задача сведена к предыдущей.






Amomum
Существует интерполяция Steffen Spline - кривая проходит через все точки без дополнительных перегибов; даже есть реализация в GSL
MichaelBorisov Автор
Это другая задача. Я решал не задачу интерполяции, а задачу аппроксимации. Интерполяция проходит через все точки, аппроксимация — нет. В том и в другом есть преимущества. Каждому инструменту — свое применение.
Иногда прохождение через все точки нежелательно. Данные могут содержать ошибки измерений. Невыгодно подгонять модель под случайные погрешности. Это приводит к проблемам, известным под названием "Overfitting".
За ссылку спасибо. Тоже интересный метод. Может пригодиться в подходящих обстоятельствах.
Amomum
Справедливо. Я чесгря никогда не мог запомнить разницу :)
Dominikanez
Классная штука. А для 3D подобное есть, не знаете?
Amomum
Не знаю, к сожалению.
MichaelBorisov Автор
Для многомерной интерполяции я бы вам порекомендовал метод, основанный на радиально-базисных функциях, в английском языке RBF. При должном подборе параметров почти всегда можно обеспечить монотонность интерполянта между узлами. Я использовал этот метод для двумерной интерполяции с нерегулярной сеткой (гексагональная, с отдельными «дырками»). Очень доволен результатами.
Если же вас интересует многомерная аппроксимация — то метод наименьших квадратов обобщается на случай многомерных многочленов и, думаю, других базовых функций.
Dominikanez
Большое спасибо, никогда ранее не слышал про RBF