14.07.2022 12:03
lfwsmrp 20 2700 Источник

Введение

На одном из собеседований по приёму на работу попросили за 30 минут написать программу, которая бы решал следующую задачу:

Есть n стандартных игральных костей (6-ти гранных кубиков) со стандартным обозначением всех граней от 1 до 6. Бросаем все n кубики разом. Нужно найти вероятность выпадения числа k, а именно суммы всех значений, выпавших на этих кубиках.

Решение

Не буду томить ожиданием и сразу выложу код алгоритма, который получился и впоследствии был немного обработан напильником.

Python
# -*- coding: utf-8 -*-

def main():
    c_int_side_dice = 6  # сколько граней у кубика
    c_int_dice_number = 6  # кол-во кубиков
    c_int_number_to_find = 18  # число, вероятность выпадения которого хотим найти
    possibility = dice_possibility(c_int_dice_number, c_int_number_to_find, c_int_side_dice)
    print(possibility)


# собственно поиск вероятности определённого значения
def dice_possibility(int_dice_number, int_number_to_find, c_int_side_dice):
    list_values, list_interm_possibility = list_values_and_interm_possibilities(int_dice_number, c_int_side_dice)
    if int_number_to_find < list_values[0] or int_number_to_find > list_values[-1]:
        # задаваемое число выходит за рамки реально возможного диапазона значений
        result_out = 0.0
    else:
        for i in range(len(list_values)):
            if list_values[i] == int_number_to_find:
                result_out = list_interm_possibility[i] / (c_int_side_dice ** int_dice_number)
                break
    return result_out


# возвращает списки/массивы: значения (сумма выпавших всех значений кубиков), сколько раз встречается значение
def list_values_and_interm_possibilities(int_dice_number, c_int_side_dice):  # [кол-во кубиков], [сколько граней у кубика]
    list_values = [i for i in range(int_dice_number, c_int_side_dice * int_dice_number + 1)]  # <длина_списков_совпадает!>
    list_interm_possibility = [1 for i in range(c_int_side_dice)]  # [1, 1, 1, 1, 1, 1]
    for i in range(int_dice_number - 1):
        list_interm_possibility = multiply_by_ones(list_interm_possibility, c_int_side_dice) # <длина_списков_совпадает!>

    return list_values, list_interm_possibility


# "умножение" на единицы
def multiply_by_ones(list_in, c_int_side_dice):  # [1, 1, 1, 1, 1, 1], 6
    list_dummy = []
    for i in range(c_int_side_dice):
        list_dummy.append([0 for j in range(i)])

    list_for_sum = []
    for i in range(c_int_side_dice):
        list_for_sum.append(list_dummy[i] + list_in + list_dummy[c_int_side_dice - i - 1])

    """
    [list_in, 0, 0, 0, 0, 0]
    [0, list_in, 0, 0, 0, 0]
    [0, 0, list_in, 0, 0, 0]
    [0, 0, 0, list_in, 0, 0]
    [0, 0, 0, 0, list_in, 0]
    [0, 0, 0, 0, 0, list_in]
    """

    list_out = []
    for i in range(len(list_for_sum[0])):
        sum_out = 0
        for j in range(c_int_side_dice):
            sum_out += list_for_sum[j][i]
        list_out.append(sum_out)

    """
    [1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1]
    """
    return list_out


main()

JavaScript
function main(){
    const c_int_side_dice = 6;  // сколько граней у кубика
    const c_int_dice_number = 6; // кол-во кубиков
    const c_int_number_to_find = 18; // число, вероятность выпадения которого хотим найти
    let possibility = dice_possibility(c_int_dice_number, c_int_number_to_find, c_int_side_dice);
    console.log(possibility);
}

// собственно поиск вероятности определённого значения
function dice_possibility(int_dice_number, int_number_to_find, c_int_side_dice){
    let lists_val_and_poss = list_values_and_interm_possibilities(int_dice_number, c_int_side_dice);
    let result_out;
    if (int_number_to_find < lists_val_and_poss[0][0] || int_number_to_find > lists_val_and_poss[0][lists_val_and_poss[0].length - 1]){
        // задаваемое число выходит за рамки реально возможного диапазона значений
        result_out = 0.0;
    } else {
        for (let i = 0; i < lists_val_and_poss[0].length; i++){
            if (lists_val_and_poss[0][i] == int_number_to_find){
                result_out = lists_val_and_poss[1][i] / Math.pow(c_int_side_dice, int_dice_number);
                break;
            }
        }
    }
    return result_out;
}

// возвращает списки/массивы: значения (сумма выпавших всех значений кубиков), сколько раз встречается значение
function list_values_and_interm_possibilities(int_dice_number, c_int_side_dice){  // [кол-во кубиков], [сколько граней у кубика]
    let list_values = new Array();
    let i = 0;
    for (let j = int_dice_number; j <= c_int_side_dice * int_dice_number; j++){
        list_values[i] = j;
        i++;
    }
    console.log(list_values);
    let list_interm_possibility = Array(c_int_side_dice).fill(1);  // [1, 1, 1, 1, 1, 1]
    for (let i = 0; i < int_dice_number - 1; i++){
        list_interm_possibility = multiply_by_ones(list_interm_possibility, c_int_side_dice);
    }
    console.log(list_interm_possibility);
    return [list_values, list_interm_possibility];
}

// "умножение" на единицы
function multiply_by_ones(list_in, c_int_side_dice){
    let list_dummy = new Array(c_int_side_dice);
    for (let j = 0; j < c_int_side_dice; j++){
        list_dummy[j] = Array(j).fill(0);
    }
    let list_for_sum = new Array(c_int_side_dice);
    for (let j = 0; j < c_int_side_dice; j++){
        list_for_sum[j] = list_dummy[j].concat(list_in, list_dummy[c_int_side_dice - j - 1]);
    }
    // [list_in, 0, 0, 0, 0, 0]
    // [0, list_in, 0, 0, 0, 0]
    // [0, 0, list_in, 0, 0, 0]
    // [0, 0, 0, list_in, 0, 0]
    // [0, 0, 0, 0, list_in, 0]
    // [0, 0, 0, 0, 0, list_in]
    
    let list_out = new Array();
    for (let i = 0; i < list_for_sum[0].length; i++){
        let sum_out = 0;
        for (let j = 0; j < c_int_side_dice; j++){
            sum_out += list_for_sum[j][i];
        }
        list_out[i] = sum_out;
    }
    // [1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1]
    return list_out;
}

main();

VBScript
Option Explicit

Sub main()
    Const c_int_side_dice = 6  'сколько граней у кубика
    Const c_int_dice_number = 3  'кол-во кубиков
    Const c_int_number_to_find = 10  'число, вероятность выпадения которого хотим найти
    Dim possibility
    possibility = dice_possibility(c_int_dice_number, c_int_number_to_find, c_int_side_dice)
    MsgBox possibility
End Sub


'собственно поиск вероятности определённого значения
Function dice_possibility(int_dice_number, int_number_to_find, c_int_side_dice)
    Dim list_values()
    Dim list_interm_possibility()
    list_values_and_interm_possibilities int_dice_number, c_int_side_dice, list_values, list_interm_possibility
    Dim result_out
    Dim i
    If int_number_to_find < list_values(0) Or int_number_to_find > list_values(UBound(list_values)) Then
        'задаваемое число выходит за рамки реально возможного диапазона значений
        result_out = 0.0
    Else
        For i = 0 To UBound(list_values)
            If list_values(i) = int_number_to_find Then
                result_out = list_interm_possibility(i) / (c_int_side_dice ^ int_dice_number)
            End If
        Next
    End If
    dice_possibility = result_out
End Function

'возвращает списки/массивы: значения (сумма выпавших всех значений кубиков), сколько раз встречается значение
Sub list_values_and_interm_possibilities(int_dice_number, c_int_side_dice, list_values, list_interm_possibility)  '[кол-во кубиков], [сколько граней у кубика]
    ReDim list_values(int_dice_number * (c_int_side_dice - 1))
    Dim i, j
    i = 0
    For j = int_dice_number To c_int_side_dice * int_dice_number
        list_values(i) = j
        i = i + 1
    Next
    ReDim list_interm_possibility(c_int_side_dice - 1)
    For j = 0 To c_int_side_dice - 1
        list_interm_possibility(j) = 1
    Next
    For j = 0 To int_dice_number - 2
        multiply_by_ones list_interm_possibility, c_int_side_dice
    Next
End Sub

'"умножение" на единицы
Sub multiply_by_ones(list_in, c_int_side_dice)
    Dim list_in_length
    list_in_length = UBound(list_in)
    Dim list_for_sum()
    ReDim list_for_sum(c_int_side_dice - 1, list_in_length + c_int_side_dice - 1)
    Dim i, j, k, n
    For i = 0 To c_int_side_dice - 1
        j = 0
        For n = 0 To c_int_side_dice - 1
            If i = n Then
                For k = 0 To list_in_length
                    list_for_sum(i, j) = list_in(k)
                    j = j + 1
                Next
            Else
                list_for_sum(i, j) = 0
                j = j + 1
            End If
        Next
    Next
    ' [list_in, 0, 0, 0, 0, 0]
    ' [0, list_in, 0, 0, 0, 0]
    ' [0, 0, list_in, 0, 0, 0]
    ' [0, 0, 0, list_in, 0, 0]
    ' [0, 0, 0, 0, list_in, 0]
    ' [0, 0, 0, 0, 0, list_in]
    ' ArrOut_2 list_for_sum
    Erase list_in
    ReDim list_in(list_in_length + c_int_side_dice - 1)
    Dim sum_out
    For j = 0 To list_in_length + c_int_side_dice - 1
        sum_out = 0
        For i = 0 To c_int_side_dice - 1
            sum_out = sum_out + list_for_sum(i, j)
        Next
        list_in(j) = sum_out
    Next
    ' [1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1]
    ' ArrOut_1 list_in
End Sub

'==================================================
'<Additional_MsgBox_For_Arrays>
Sub ArrOut_1(arr_in)
    Dim str_out
    Dim i
    For i = 0 To UBound(arr_in)
        If i = 0 Then
            str_out = arr_in(i)
        Else
            str_out = str_out & " " & arr_in(i)
        End If
    Next
    MsgBox str_out
End Sub

Sub ArrOut_2(arr_in)
    Dim str_out
    Dim i, j
    For i = 0 To UBound(arr_in, 1)
        For j = 0 To UBound(arr_in, 2)
            If i = 0 And j = 0 Then
                str_out = arr_in(i, j)
            ElseIf j = 0 Then
                str_out = str_out & vbNewLine & arr_in(i, j)
            Else
                str_out = str_out & " " & arr_in(i, j)
            End If
        Next
    Next
    MsgBox str_out
End Sub
'</Additional_MsgBox_For_Arrays>
'==================================================

main

Пояснение

Понятно, что копание в чужом коде — дело не благодарное, опишу работу алгоритма для одного конкретного примера.

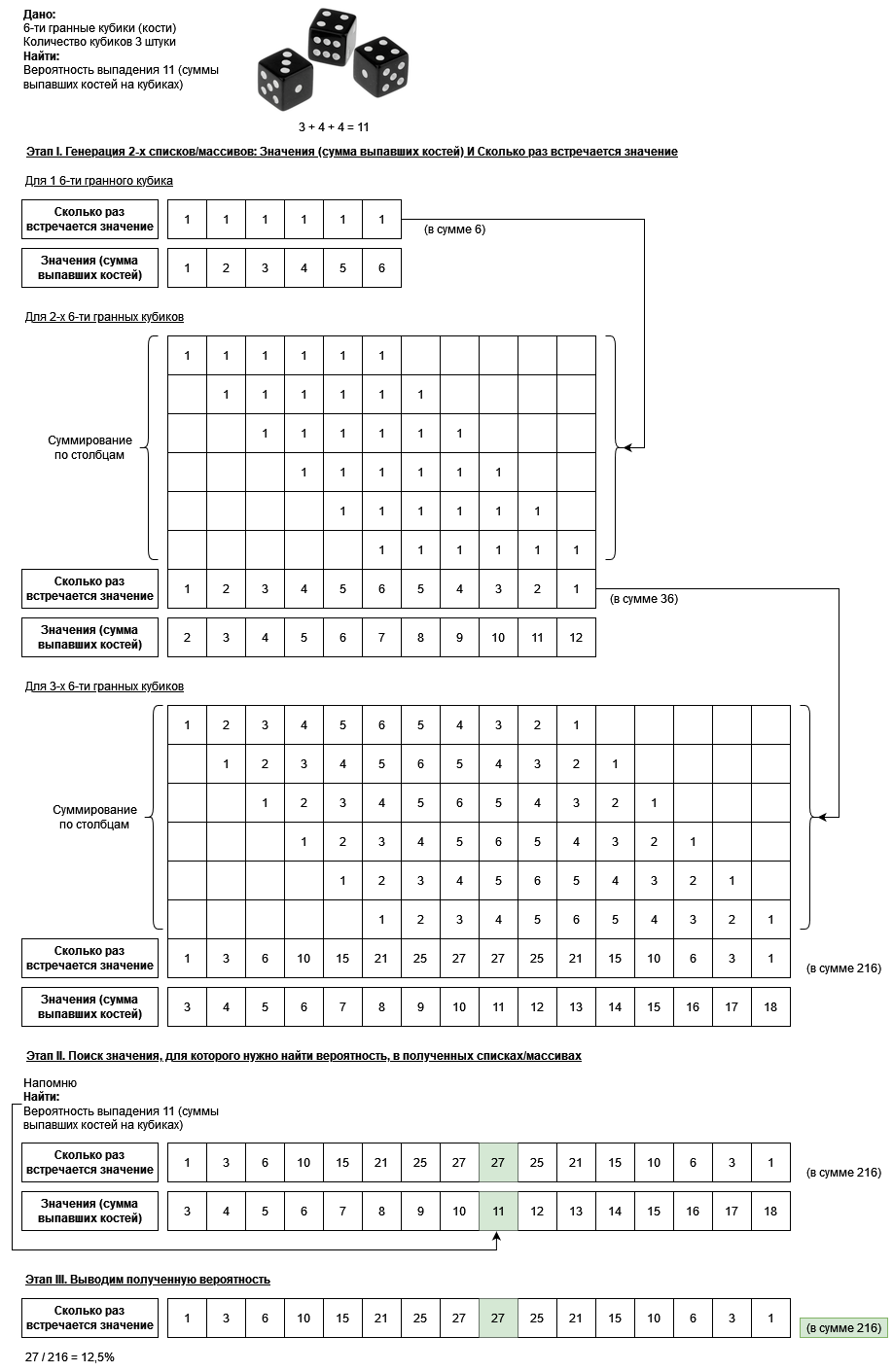
Смею предположить, что дочитав до этого момента у многих читателей уже зародятся скептические настроения, однако в свою очередь предложу поверить самостоятельно и в помощь приложу SQL запрос, который считает «в лоб», т.е. генерирует все возможные комбинации выпадения для 3-х кубиков, а потом пересчитывает все выпавшие суммы. В результате отработки скрипта мы получим 2 столбца из самого конца пункта “Этап I. Генерация 2-х списков/массивов: Значения (сумма выпавших костей) И Сколько раз встречается значение”.

SQL запрос - генератор решения "в лоб"
-- заводим значения сторон кубика
WITH step_01_insert (dice) AS (
    SELECT 1 AS dice UNION ALL
    SELECT 2 AS dice UNION ALL
    SELECT 3 AS dice UNION ALL
    SELECT 4 AS dice UNION ALL
    SELECT 5 AS dice UNION ALL
    SELECT 6 AS dice
)
-- генерируем все возможные ситуации для 3-х кубиков
, step_02_spawn (dice_1, dice_2, dice_3, dice_sum) AS (
    SELECT T1.dice AS dice_1
    , T2.dice AS dice_2
    , T3.dice AS dice_3
	, T1.dice + T2.dice + T3.dice AS dice_sum -- Значения (сумма выпавших костей)
    FROM step_01_insert AS T1
    , step_01_insert AS T2
    , step_01_insert AS T3
)
-- считаем в лоб, сколько раз встречается значение
SELECT dice_sum  -- Значения (сумма выпавших костей)
, COUNT(1) AS num  -- Сколько раз встречается значение
FROM step_02_spawn
GROUP BY dice_sum
ORDER BY dice_sum;

dice_sum

num

3

1

4

3

5

6

6

10

7

15

8

21

9

25

10

27

11

27

12

25

13

21

14

15

15

10

16

6

17

3

18

1

Конечно это не достаточно для полноценного доказательства, о котором я расскажу чуть позже, но хоть накал скепсиса, надеюсь, мне удалось сбавить.

Отмечу, что я не претендую на какую-то оригинальность, т.к. подобный алгоритм упоминается в данных статьях: "How to Calculate Multiple Dice Probabilities" Method 2 Recursion, "Как посчитать вероятность определенной комбинации при игре в кости" Метод 2 Рекурсия (перевод).

Пусть вас не смущает хитрое смещение суммирования в формуле Excel – суть от этого никак не меняется. Явно именно раздел «Метод 2» затачивался под Excel реализацию, но запрограммировать данный алгоритм в лоб без изменений именно на каком-либо языке программирования — задача не тривиальная.

Но всё-таки, почему этот алгоритм работает?

Для начала вспомним треугольник Паскаля:

Из всего множества его замечательных свойств я бы хотел заострить внимание на следующем: до строки:

цифры в треугольнике Паскаля повторяют степени числа 11 в степени 1<=k<=4 (натуральное). Но это утверждение верно для десятичной системы счисления, однако, если считать степень числа 11 в шестнадцатеричной системе счисления, то можно продлить совпадения до 1<=k<=5.

Можно задаться вопросом: а на каком калькуляторе можно 11 возводить в степень 5 в шестнадцатеричной системе счисления? Ответ: воспользуемся свойством

Иначе говоря идём итерационно:
121=11 * 11
1331=121 * 11
14641=1331 * 11
15AA51=14641 * 11

Давайте чуть здесь остановимся и вспомним школьную программу, а именно умножение в столбик, с одной лишь оговоркой, что перенос числа из одного разряда в другой (при переполнении разряда) буду делать отдельной операцией, а так же визуально для каждого разряда выделю отдельный столбец.
Пример 1.
14641 * 11 в десятеричной системе счисления.

  1. Заполняем условия.

  2. Записываем результаты умножения каждой единицы разряда.

  3. Суммируем.

  4. Переводим из переполнившихся разрядов в разряды выше.

Проделаем ту же операцию в шестнадцатеричной системе счисления (Шестнадцатеричная система счисления)
Пример 2.

  1. Заполняем условия.

  2. Записываем результаты умножения каждой единицы разряда.

  3. Суммируем.

  4. Записываем полученные числа правильно в шестнадцатеричной системе счисления.

И для закрепления ещё один.
Пример 3.
15AA51 * 11 в шестнадцатеричной системе счисления.

  1. Заполняем условия в шестнадцатеричной системе счисления.

  2. Переводим запись из шестнадцатеричной в десятичную систему счисления для улучшения восприятия (благо мы можем себе это позволить, т.к. визуально отделяем каждый разряд друг от друга).

  3. Записываем результаты умножения каждой единицы разряда.

  4. Суммируем.

  5. Переводим поэтапно из переполнившихся разрядов в разряды выше.

  6. Записываем полученные числа правильно в шестнадцатеричной системе счисления.

Во всех приведённых примерах я бы акцентировал внимание на пунктах «Суммируем» (Пример 1 - п3., Пример 2 - п3., Пример 3 - п4.), которые «цитируют» одну из строк треугольника Паскаля. Если продолжить мысль, то манипуляции с разрядами мешают нормальному воспроизведению всего треугольника. А давайте от них избавимся? Т.е. условно говоря будем считать (да простят меня математики) в «условно бесконечной системе счисления» (вероятно есть и более адекватный термин, но увы, беглый запрос по интернету ничего не дал, что больше доказывает мою лень, а не на отсутствие информации как таковой), т.е. когда перехода из одного разряда в другой при операции сложения не происходит. И это работает:

Тут я не претендую опять же на оригинальность, данный метод есть и им пользуются: как вывести треугольник Паскаля на Python? (см. «Простейшая реализация»)

Вернёмся к кубикам.

Посчитаем в лоб сколько раз встречается сумма костей для всех возможных случаев.

1 кубик (тут всё просто).

2 кубика (идём по классике жанра).

Тут конечно можно посчитать вручную, т.е. просуммировать все единицы в правой таблице, соответствующие полученным значениям в левой таблице (лучше визуализировать):

Однако, заметим смещение и преобразуем обе таблицы следующим образом:

После этого в правой таблице нам останется лишь просуммировать строки. Опять же тут немного остановимся на правой табличке, и заметим, что она напоминает уже упомянутое выше умножение столбик в десятичной системе счисления.

В итоге получим:

Проделаем аналогичные шаги для 3-х кубиков:

Смещаем:

Акцентируем внимание, что опять же правая таблица напоминает умножение в столбик в «условно бесконечной системе счисления»:

Выводим результат:

Описанные операции итерационно можно продолжать сколь угодно долго.

Данный алгоритм походит для любого числа одинаковых игровых кубиков с любым количеством граней, у которых числа на гранях входят в арифметическую последовательность. И его при некотором желании можно даже модифицировать и для решения задач, когда речь идёт не об однотипных кубиках а с разным количеством граней (правда я ума не приложу кому это может понадобиться).

Итого, выводы

  1. Задачи на поиск вероятности выпадения числа k у n игральных кубиков попадаются на собеседованиях.

  2. В данной статье рассмотрен довольно элегантный алгоритм по решению подобных задач, указанных выше. В принципе можно решать подобные задачи просто на листе бумаге.

О чём стоит упомянуть
Представленный алгоритм не является самым оптимальным. Например для 1000 кубиков (не знаю кому это будет нужно, но вдруг) придётся просчитать для всех элементов последовательности 1000 раз. Но можно ещё поиграться с умножением в столбик в «условно ...» и снизить вычислительную сложность алгоритма с O(n) до O(log(n)) ("Оценка сложности алгоритмов, или Что такое О(log n)").

Комментарии (20)


  1. akhalat
    14.07.2022 13:08
    #24527044
    +2

    Задача, кстати, точно решается («на листе бумаги»):
    towardsdatascience.com/modelling-the-probability-distributions-of-dice-b6ecf87b24ea?gi=ff1c8764fd6c


    1. matabili1973
      14.07.2022 13:43
      #24527218

      По факту конкретный математический пример решается даже без привлечения терминологии и обозначений теории вероятности. Есть вероятность благоприятного исхода, которая зависит от количества кубиков. Есть количество благоприятных исходов. Произведение этих величин - это и есть искомая вероятность.

      Но здесь, я так понял, задача состоит именно в том, чтобы написать алгоритм, который будет автоматически рассчитывать вероятность выпадения произвольной суммы с произвольным количеством кубиков?


  1. xi-tauw
    14.07.2022 13:44
    #24527222
    +3

    Давайте посмотрим на исходную задачу "в лоб". Переформулируем ее в необходимость найти f(n, k) - функцию, которая вычисляет количество вариантов получить число n при броске k кубиков.

    Пограничные случаи: если n < k или n > 6k, то значение 0.

    Если k = 1, то результат 1 (все, кроме чисел от 1 до 6 отсечено выше, а эти числа можно получить только одним образом каждое).

    И общий случай: пусть на первом кубике выпало 1, тогда нужно посмотреть сколькими способами можно получить n-1 броском k-1 кубика, если выпало 2, то сколько способов для n-2 те ми же k-1 кубиками. В общем f(n-1, k-1)+f(n-2, k-1)+f(n-3, k-1)+f(n-4, k-1)+f(n-5, k-1)+f(n-6, k-1).

    Итого:

    int f(int n, int k)
{
    if (n < k)
        return 0;
    if (n > 6*k)
        return 0;
    if (k == 1)
        return 1;
    return f(n-1, k-1)+f(n-2, k-1)+f(n-3, k-1)+f(n-4, k-1)+f(n-5, k-1)+f(n-6, k-1);
}

    Добавляем сверху кэширование результатов, чтобы не вычислять уже вычисленное и готово.

    Смотрим на ваш способ и видим, что он по сути такой же:

    Вот как раз визуальная иллюстрация: для трех кубиков считаем количества сумм брошенных двумя кубиками со сдвигом.

    То есть ваш способ очевидно корректен, он будет оперировать ровно теми же числами, что попадут в кэш в простом способе. Но вот что ваш код и объяснения легче, я бы не сказал.


  1. DeadKennady
    14.07.2022 13:50
    #24527250
    -1

    Думаю, можно было бы воспользоваться разбиением чисел.
    То есть мы берем 18 и пытаемся представить его как сумму шести чисел от 1 до 6.
    Например, таким образом:

    ```python

    def partition(n,k,l,m):
    if k < 1:
    return
    if k == 1:
    if n <= m and n>=l :
    yield (n,)
    return
    for i in range(l,m+1):
    for result in partition(n-i,k-1,i,m):
    yield result+(i,)

    x = list(partition(18 ,6, 1, 6 ))
    print('x',x)

    ```

    И потом для каждого полученного разложения найти количество перестановок -- это даст нам число всех благоприятных исходов.


  1. artemsnad
    14.07.2022 16:21
    #24527824

    Немного режет глаз слово "possibility". Всё же оно переводится как возможность, а вероятность - probability.


    1. lfwsmrp Автор
      15.07.2022 11:02
      #24529908

      Упс, согласен, не усмотрел, спасибо!

      По возможности заменю во всех скриптах программ с "possibility" на "probability"


  1. Parramon
    14.07.2022 16:22
    #24527830
    +1

    Ровно тот же результат при решении еще более "в лоб":

    n=3
d = 6
s=d ** n
ps = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

for d1 in range(1, d+1):
    for d2 in range(1, d+1):
        for d3 in range(1, d+1):
            ps[d1+d2+d3] += 1
print(s)
print(ps)
print(ps[11]/s*100)


    1. unitby
      15.07.2022 13:34
      #24530404

      n = 3
dn = 6
s = dn ** n
ps = [0] * (n * dn + 1)
f = 11


def func(level, current):
    for d in range(1, dn+1):
        if level == 1:
            ps[current+d] += 1
        else:
            func(level-1, current+d)


func(n, 0)
print(s)
print(ps)
print(ps[f]/s*100)

      чтобы n можно было указывать достаточно в рекурсию обернуть


  1. pavelthebest
    14.07.2022 17:57
    #24528178
    +1

    Что интересно, эту задачу можно решить намного оптимальнее, чем предложено как в статье, так и в других комментариях (я не нашёл чего-то существенно лучше O(n^2)): например, за O(n \log^2 n).

    Для формальности пусть наш кубик будет не обычный игральный, а с числами 1, 2, \ldots, d.

    Заметим, что нам достаточно найти f(n, k) – количество способов набрать сумму k, после n бросков. Тогда вероятность можно получить, разделив f(n, k) на d^k.

    Подставив разные результаты выпадения последнего кубика, получаем f(n, k) = f(n - 1, k - 1) + f(n - 1, k - 2) + \ldots + f(n - 1, k - d).

    Заметим, что f(n, k) это просто коэффициент многочлена (x + x^2 + x^3 + \dots + x^d)^n при x^k.

    Я не умею эффективно находить в отдельности k-й коэффициент, поэтому давайте найдём многочлен целиком.

    Для этого воспользуемся бинарным возведением в степень: это позволит нам найти искомый многочлен всего за O(\log n) перемножений многочленов. Перемножать многочлены можно при помощи быстрого преобразованием Фурье за O(n \log n).
    Итоговая асимптотика: O(n \log^2 n).

    С небольшими изменениями это же решение можно использовать для кубиков разных размеров (например, для x бросков d125 и y бросков d512).


    1. wataru
      15.07.2022 17:19
      #24531158

      Вот только длина многочлена там не n, а n*d, так что ассимптотика в общем случае указана не совсем точно. Но для констнтного d=6 — это действительно более быстрый метод. Правда есть вообще за O(n), развивающий вашу идею с производящими функциями, указанный в комментарии выше akhalat:
      https://towardsdatascience.com/modelling-the-probability-distributions-of-dice-b6ecf87b24ea


      1. akhalat
        16.07.2022 01:44
        #24532076

        Идея с тем что число всех комбинаций просто будет коэффициентом при соответствующей степени в многочлене реально прикольная, и по сути служит краеугольным камнем точного решения. Остальное всё — техника.


        1. wataru
          16.07.2022 11:31
          #24532474

          Ага. Это называется "метод производящей функции".


          1. akhalat
            16.07.2022 18:09
            #24533150

            Это называется «метод производящей функции».

            В курсе, и основная проблема всегда — найти эту производяющую функцию. В данном случае это делается весьма остроумно.


  1. Riim
    14.07.2022 19:00
    #24528312
    +2

    На одном из собеседований по приёму на работу попросили за 30 минут написать программу

    Задачка, конечно, интересная, но по мне так идиотизм давать такое на очном собесе ещё и с ограничением по времени. Даже сильный специалист банально из-за волнения может затупить с вероятностью 50/50. Результат будет совершенно не показательный, зато уверенно пройдёт отлимпиадник с нулевым опытом реальной разработки. Если такой и нужен, то ок конечно, но по мне так лучше давать несколько мелких, но хитрых задачек по 3-7 минут на каждую и смотреть по кол-ву решённых. Причём, начинать нужно с наиболее лёгких -- сбить волнение.
    Говорю это на собственном опыте, на одних собесах без проблем решал подобное, особенно когда вакансия не особо интересна и больше по приколу собес проходишь, на других начинаешь чуть тупить, из-за этого волнуешься, от волнения ещё больше тупишь и так по кругу. Результат околонулевой, после собеса уже спокойно садишься и через 15 минут получаешь рабочее решение. Только работодатель уже не поверит, что я его сам получил, а не в интернете нашёл.
    Хороший пример с Яндексом, куда я дважды устраивался. Первый раз собеседующий начал закидывать меня мелкими задачками, каждая легко решалась знанием какой-то фичи языка, но можно было и без этого обойтись. В конце он сказал, что я первый кто всю его коллекцию успел решить, большинство около трети решают. При втором устройстве было два коротких собеса минут по 30-40 и задачи уже явно больше, хоть и не как в статье. На первом решил две, на втором первую и жёстко затупил на второй. В результате два собеса с хорошим результатом и один с плохим. Так это точно не должно работать.


    1. lfwsmrp Автор
      15.07.2022 10:54
      #24529878

      Задачка, конечно, интересная, но по мне так идиотизм давать такое на очном собесе ещё и с ограничением по времени. Даже сильный специалист банально из-за волнения может затупить с вероятностью 50/50. Результат будет совершенно не показательный, зато уверенно пройдёт олимпиадник с нулевым опытом реальной разработки

      Скажу осторожно, что больше соглашусь.

      Если рассказывать про мой опыт, то эту задачку я писал минут 40-45 (т.е. в 30 минут не уложился), учитывая, что случайно нечто подобное я решал лет 8 назад чисто для себя.

      Почему не на 100% соглашусь.

      Предположу, что для случая с "тупняком" собеседуемого, возможно опрашивающий уже имел заготовленный сценарий как направлять мысли в правильное русло наводящими вопросами


  1. wataru
    15.07.2022 17:15
    #24531146
    -1

    и снизить вычислительную сложность алгоритма с O(n) до O(log(n))

    У вас алгоритм работает за O(n^2) (но реализован он через такую задницу, что там константы на куб хватит и еще на логарифм останется). Я бы постыдился вот это выставлять на всеобщее обозрение и еще пытаться объяснять.


    1. lfwsmrp Автор
      16.07.2022 11:13
      #24532436

      Озвучу очевидное: чтобы что-то объяснить не нужно писать идеальный код, он должен быть достаточен для понимания, желательно с разделёнными смысловыми блоками.

      Я бы постыдился вот это выставлять на всеобщее обозрение

      Не стоит комплексовать - ничто не идеально.

      У меня не было цели описывать все возможные варианты решения и тем более сравнивать их между собой. Один метод показался занятным - его и расписал. А объяснение - оно работает.

      По поводу O(n^2) - наврал, согласен, исправлю


      1. wataru
        16.07.2022 11:40
        #24532498

        ничто не идеально.

        Да. Но неужели у вас при написании, например, вот этого куска кода ничего не напряглось внутри?


        for i in range(len(list_values)):
    if list_values[i] == int_number_to_find:
        result_out = list_interm_possibility[i] / (c_int_side_dice ** int_dice_number)
        break

        Его же можно заменить на


        result_out = list_interm_possibility[int_number_to_find - list_values[0]] / (c_int_side_dice ** int_dice_number)

        И тут должно стать понятно, что вам вообще не нужен список list_values. Он даже у вас в коде элементарно вычисляется.


        1. lfwsmrp Автор
          16.07.2022 12:00
          #24532524

          И тут должно стать понятно, что вам вообще не нужен список list_values. Он даже у вас в коде элементарно вычисляется.

          Абсолютно верно

          вот этого куска кода ничего не напряглось внутри?

          Подтвержу, напряглось. Однако же для пояснения алгоритма ниже вывожу вот такую картинку:

          Т.е. хочется какого-то единообразия и в пояснении и в коде. Иначе если я напишу в коде одно а в пояснении другое, ну согласитесь как минимум будет небольшой ступор у читающего (как максимум - недоверие: пишет в коде одно, а описывает другое)

          И тут должно стать понятно, что вам вообще не нужен список list_values. Он даже у вас в коде элементарно вычисляется.

          И тут согласен на все 100%

          Но в пояснениях оперирую массивами/списками и в коде сознательно иду на этот шаг, чтобы повествование не отходила от кода (или точнее наоборот чтобы код не отходил от повествования).


          1. wataru
            16.07.2022 12:24
            #24532564

            Вы очень намудрили и с решением и с объяснением.


            Все ваше объяснение упрощается и ужимается до:
            Давайте считать, сколько способов получить все возможные суммы бросив 1,2… n кубиков. Когда мы бросаем k кубиков мы можем получить значения от k (все по 1) до 6*k (все по 6). Примеры (показываем массив с индексами. Числа в квадратиках, индексы над ними):


            k=1
1 2 3 4 5 6 
1 1 1 1 1 1
k=2
2  3  4  5  6  7  8  9 10 11 12
1  2  3  4  5  6  5  4  3  2  1

            Для подсчета каждого значения для k надо сложить 6 предыдущих значений для k-1, ведь последняя кость может принять значения 1..6 и потом каждый способ получить оставшуюся сумму k-1 кубиком дает новый способ получить всю сумму вместе с последним кубиком. Вот и получается, что массив для следующего k — это сумма 6 массивов для предыдущего k, сдвинутые на 1..6 вправо. Тут можно показать картинку как один массив получается из предыдущего суммой в столбик.


            Можно не хранить нули, а только значения от k до 6*k — тогда надо к массиву прибавить 5 его сдвинутых копий и помнить, что начало всегда дает значение для суммы = k. Или можно представить, что на кубиках не числа 1..6, а 0..5. Тогда вам надо просто вычесть из искомой суммы количество кубиков, чтобы перейти к новой задаче.


            Вот весь код:


            def dice_possibility(int_dice_number, int_number_to_find, c_int_side_dice):
  if int_number_to_find < int_dice_number or int_number_to_find > c_int_side_dice*int_dice_number:
    return 0;
  counts = [1]*6; # Бросок одной кости.
  for k in range(2, int_dice_number+1):
    next_counts = [0]*(len(counts) + 5)
    for shift in range(0, c_int_side_dice):
      for i in range(0, len(counts)):
        # Прибавляем копию массива со сдвигом shift.
        next_counts[i+shift] += counts[i];
    counts = next_counts
  return counts[int_number_to_find - int_dice_number] / c_int_side_dice**int_dice_number

            Что делает этот код понятно любому чуть знакомому с питоном. Почему этот код работает понятно и из одного абзаца перед кодом. И не надо писать всякие извращения.


            А вообще, все объяснение заменяется двумя словами "динамическое программирование". Но алгоритмы же программистам знать не надо.