Проверка нормальности распределения с использованием критерия Эппса-Палли средствами Python / forpes.ru

Главная
Проверка нормальности распределения с использованием критерия Эппса-Палли средствами Python

Проверка нормальности распределения с использованием критерия Эппса-Палли средствами Python +4

31.08.2022 11:00

ANazarov 0 758 Источник

Постановка задачи

Критерий Эппса-Палли - один из критериев проверки нормальности распределения, основанный на сравнении эмпирической и теоретической характеристических функций.

Критерий предложен в 1983 г. (см. Epps, T. W., and Pulley, L. B. (1983). A test for normality based on the empirical characteristic function. Biometrika 70, 723–726). В настоящее время данный критерий рекомендован к использованию в ГОСТ Р ИСО 5479-2002 [1, с.13], однако среди тестов, включенных в модуль scipy.stats, данный критерий, к сожалению, отсутствует.

Детальное исследование критерия Эппса-Палли проведено в работах Б.Ю. Лемешко ([2], [3] и др.). Так, было установлено [3, с.31, 80], что по мощности критерий Эппса-Палли превосходит критерии Шапиро-Уилка, Д'Агостино, Дэвида-Хартли-Пирсона, однако имеет недостаток - при малых объемах выборки неспособен отличать от нормального закона распределения с более плоскими плотностями распределений (с коэффициентом эксцесса Es < 2); впрочем этот недостаток также свойственен и критерию Шапиро-Уилка.

Также про достоинства критерия Эппса-Палли - см., например, Bahadur efficiencies of the Epps–Pulley test for normality.

В ГОСТ Р ИСО 5479-2002 критерий Эппса-Палли рекомендуется применять при n ≥ 8, табличные значения приведены для 8 ≤ n ≤ 200. В работе Б.Ю. Лемешко [3, с.33] критерий рекомендуется применять при n > 15, табличные значения приведены для 8 ≤ n ≤ 1000.

Представляет интерес рассмотреть способы реализации критерия Эппса-Палли средствами python, добавив это весьма неплохой критерий в инструментарий специалиста DataScience.

Формирование исходных данных

В качестве исходных данных рассмотрим примеры, разобранные в работе Лемешко Б.Ю. [3, с.138-146], а именно:

результаты измерения средней плотности Земли (эксперимент Кавендиша);
результаты измерения заряда электрона (эксперимент Милликена);
результаты измерения скорости света (эксперимент Майкельсона);
результаты измерения скорости света (эксперимент Ньюкомба).

Рассмотрим для начала результаты измерения средней плотности Земли, полученные Генри Кавендишем, (г/см3) [3, с.139, табл.5.1]:

X = np.array([
    5.50, 5.55, 5.57, 5.34, 5.42, 5.30, 5.61, 5.36, 5.53, 5.79,
    5.47, 5.75, 4.88, 5.29, 5.62, 5.10, 5.63, 5.68, 5.07, 5.58,
    5.29, 5.27, 5.34, 5.85, 5.26, 5.65, 5.44, 5.39, 5.46
    ])

Выполним предварительную визуализацию с помощью пользовательской функции graph_hist_boxplot_probplot_sns, которая позволяет визуализировать исходную выборку путем одновременного построения гистограммы, коробчатой диаграммы и вероятностного графика, тем самым давая возможность исследователю одним взглядом оценить свойства выборки. Данная функция загружается из пользовательского модуля my_module__stat.py (функция graph_hist_boxplot_probplot_sns и модуль my_module__stat.py доступны в моем репозитории на GitHub https://github.com/AANazarov/MyModulePython).

graph_hist_boxplot_probplot_sns(
    data=X,
    graph_inclusion='hbp',    # выбор вида визуализации: h - hist, b - boxplot, p - probplot
    title_axes='Эксперимент Кавендиша', title_axes_fontsize=16,
    data_label='Средняя плотность Земли (г/см3)')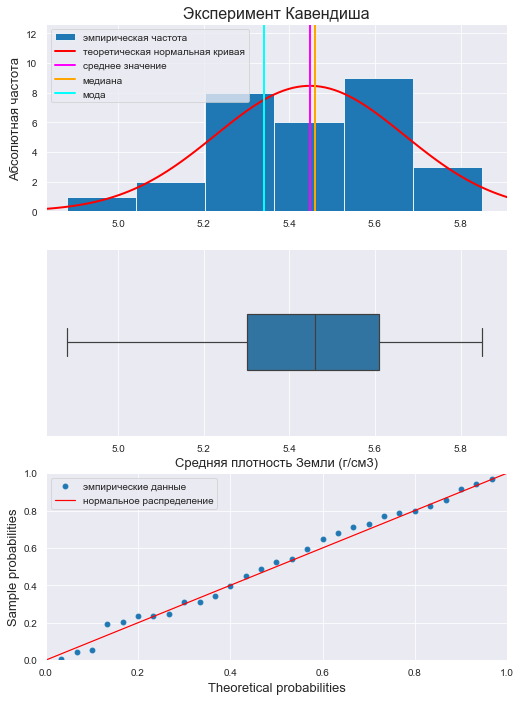

Проверка нормальности распределения по критерию Эппса-Палли

1. Расчет статистики критерия Эппса-Палли

Определим расчетное значение статистики критерия Эппса-Палли по методике, приведенной в ГОСТ Р ИСО 5479-2002.

Объем выборки:

N = len(X)
print(f'N = {N}')

Находим характеристики выборки - среднее арифметическое и центральный момент 2-го порядка (дисперсия для генеральной совокупности, без поправки на смещенность):

# среднее арифметическое
X_mean = X.mean()
print(f'Xmean = {X_mean}')

# центральный момент 2-го порядка
m2 = np.var(X, ddof = 0)
print(f'm2 = {m2}')

Вычислим величину A:

A = sqrt(2) * np.sum([exp(-(X[i] - X_mean)**2 / (4*m2)) for i in range(N)])
print(f'A = {A}')

Вычислим величину B:

B = 2/N * np.sum(
    [np.sum([exp(-(X[j] - X[k])**2 / (2*m2)) for j in range(0, k)]) 
     for k in range(1, N)])
print(f'B = {B}')

Расчетное значение статистики критерия Эппса-Палли:

TEP_calc = 1 + N / sqrt(3) + B - A
print(f'Расчетное значение статистики критерия Эппса-Палли: TEP_calc = {TEP_calc}')

Рассчитанное нами значение совпадает с приведенным в источнике [3, с.143].

2. Определение табличных значений статистики критерия Эппса-Палли

В табл.12 ГОСТ Р ИСО 5479-2002 приведены табличные значения статистики критерия Эппса-Палли для 8 ≤ n ≤ 200:

В работе Б.Ю. Лемешко [3, с.185] приведены табличные значения статистики критерия Эппса-Палли для 8 ≤ n ≤ 1000:

Сформируем csv-файл с табличными значениями (для дальнейшего использования), поместим его в папку table в том же каталоге, что и наш рабочий файл *.ipynb:

Tep_table_df = pd.read_csv(
    filepath_or_buffer='table/Tep_table.csv',
    sep=';',
    index_col='n')
display(Tep_table_df)

Промежуточные значения определим с помощью интерполяции - для этого создадим пользовательскую функцию:

def Tep_table(n, p_level=0.95):
    # загружаем табличные значения статистики критерия Эппса-Палли
    Tep_table_df = pd.read_csv(
        filepath_or_buffer='table/Tep_table.csv',
        sep=';',
        index_col='n')
    # выбираем величину доверительной вероятности
    p_level_dict = {
        0.9:   Tep_table_df.columns[0],
        0.95:  Tep_table_df.columns[1],
        0.975: Tep_table_df.columns[2],
        0.99:  Tep_table_df.columns[3]}
    # линейная интерполяция
    N = Tep_table_df.index
    T = Tep_table_df[p_level_dict[p_level]]
    f_lin = sci.interpolate.interp1d(N, T)
    result = float(f_lin(n))    
    return result

Визуализация табличных значений статистики критерия Эппса-Палли:

fig, axes = plt.subplots(figsize=(297/INCH, 210/INCH))
axes.set_title('Табличные значения статистики критерия Эппса-Палли', fontsize=16)
axes.plot(Tep_table_df.index, Tep_table_df['p=0.9'].values, 'ob-', label='p=0.9')
axes.plot(Tep_table_df.index, Tep_table_df['p=0.95'].values, 'og-', label='p=0.95')
axes.plot(Tep_table_df.index, Tep_table_df['p=0.975'].values, 'oc-', label='p=0.975')
axes.plot(Tep_table_df.index, Tep_table_df['p=0.99'].values, 'om-', label='p=0.99')
axes.legend(loc="best", fontsize=12)
axes.set_xlim(0, 1000)
axes.set_ylim(0.2, 0.7)
axes.set_xlabel('n')
axes.set_ylabel('Tep(n)')

3. Аппроксимация предельных распределений статистики критерия Эппса-Палли

В работе Б.Ю. Лемешко [3, с.32] указано, что распределение статистики критерия Эппса-Палли достаточно хорошо аппроксимируется бета-распределением III рода, плотность распределения которого имеет вид:

Там же указано, что при 15 < n < 50 можно использовать бета-распределениями III рода с параметрами:

θ0 = 1.8645    θ1 = 2.5155    θ2 = 5.8256    θ3 = 0.9216    θ4 = 0.0008

При n ≥ 50 следует пользоваться предельным распределением с параметрами:

θ0 = 1.7669    θ1 = 2.1668    θ2 = 6.7594    θ3 = 0.91    θ4 = 0.0016

Теперь для выполнения расчетов нам необходимо сопоставить встроенные возможности python с указанным выше распределением.

Библиотека scipy дает нам возможность работать с бета-распределением (https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.beta.html), плотность которого имеет вид:

Так как бета-функция выражается через гамма-функцию:

то очевидно, что мы имеем дело с классическим бета-распределением, разобранным в множестве источников (например, [4, 5, 6]). При этом во всех указанных источниках упоминаний про бета-распределение III рода нет. Соответственно, и python не имеет встроенных возможностей для работы с данным распределением.

Следует разобраться более подробно с этим распределением. Это представляет интерес еще и потому, что в работах [2], [3], посвященных исследованию распределений подобная ситуация встречается часто - распределения статистик различных критериев описываются малораспространенными видами распределений, которые не реализованы в python, то есть с подобной проблемой исследователь может столкнуться при решении других задач. Ну об этом напишем в другой раз, в этой области огромное количество интересных и полезных методов и задач.

Кстати, на основании исследований Б.Ю. Лемешко и его коллектива были разработаны рекомендации по стандартизации:

Р 50.1.033-2001. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть I. Критерии типа хи-квадрат.
Р 50.1.037-2002. Рекомендации по стандартизации. Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть II. Непараметрические критерии.

На сегодняшний день они имеют статус действующих.

Итак, в отечественной литературе по прикладной статистике понятие бета-распределения III рода (а, соответственно I и II рода) до начала 1990-х гг., мне обнаружить не удалось.

В интернете информации тоже немного, хотя кое-что найти можно (например, https://www.r-bloggers.com/2019/07/the-beta-distribution-of-the-third-kind-or-generalised-beta-prime/).

Более или менее подробный теоретический материал удалось обнаружить в кандидатской диссертации Постовалова С.Н. [7, с.92-95, 111-115], научным руководителем которого был Б.Ю. Лемешко. Постовалов С.Н. в своей работе [7, с.113] ссылается на работу Губарева В.В. [8], в которой и приводятся справочные данные о бета-распределения III рода [8, табл.4.3, п.27, с.164], при этом данной распределение отмечено примечанием "введено автором". То есть получается, что понятие бета-распределения III рода предложено Губаревым В.В. в 1992 г. и, очевидно, характерно только для отечественной, в частности, новосибирской, школы прикладной статистики? Так это или иначе, но неудивительно, что в python это распределение не реализовано. Реализуем сами.

Итак, Постовалов С.Н. в своей работе [7, с.92] дает следующее определение бета-распределения III рода: если рассмотреть обобщенное семейство бета-распределений, функция распределения которых имеет вид:

где:

то, используя генерирующую функцию вида:

мы и получим бета-распределение III рода.

То есть мы видим, что с помощью генерирующей функции мы можем перейти от обычного бета-распределения (или бета-распределения I рода, как оно именуется в [7]), которое реализовано в библиотеке scipy, к бета-распределению III рода, что нам и требуется.

4. Реализация бета-распределения III рода средствами python

Функция обычного бета-распределения (I рода) реализована в модуле scipy.stat следующим образом:

сdf_beta_I = lambda x, a, b: sci.stats.beta.cdf(x, a, b, loc=0, scale=1)

Перейдем к функции бета-распределения III рода с помощью генерирующей функции [7, с.92]:

g_beta_III = lambda z, δ: δ*z / (1+(δ-1)*z)

Подставляя g_beta_III в сdf_beta_I, получим функцию бета-распределения III рода:

cdf_beta_III = lambda x, θ0, θ1, θ2, θ3, θ4: сdf_beta_I(g_beta_III((x - θ4)/θ3, θ2), θ0, θ1)

При этом важно идентифицировать параметры функции распределения, так как в разных источниках используются различные обозначения. В рассматриваемом нами источнике у Б.Ю. Лемешко [3] используются параметры θ0, θ1, θ2, θ3, θ4, будем идентифицировать их:

График функции бета-распределения III рода:

# набор параметров распределения для 15 < n < 50
θ_1 = (1.8645, 2.5155, 5.8256, 0.9216, 0.0008)
# набор параметров распределения для n >= 50
θ_2 = (1.7669, 2.1668, 6.7594, 0.91, 0.0016)

fig, axes = plt.subplots(figsize=(210/INCH, 297/INCH/2))
axes.set_title('Функция бета-распределения III рода \nпри аппроксимации распределения статистики критерия Эппса-Палли', fontsize=14)
xmin = 0
xmax = 1
x = np.linspace(xmin, xmax, 100)
axes.plot(x, cdf_beta_III(x, θ_1[0], θ_1[1], θ_1[2], θ_1[3], θ_1[4]), label='для 15 < n < 50')
axes.plot(x, cdf_beta_III(x, θ_2[0], θ_2[1], θ_2[2], θ_2[3], θ_2[4]), label='для n >= 50')
axes.legend(loc="best", fontsize=12)
axes.set_xlim(xmin, xmax)
axes.set_xlabel('x')
axes.set_ylabel('cdf_beta_III(x)')

5. Плотность бета-распределения III рода

Для использования критерия Эппса-Палли плотность плотности распределения нам, по сути, не нужна, но, тем не менее, найдем ее, так сказать, для общей демонстрации возможностей.

Для нахождения плотности бета-распределения III рода мы не можем воспользоваться встроенными возможностями модуля scipy.stat. Придется воспользоваться определением плотности распределения как первой производной от функции распределения. При этом у нас не получится найти эту производную в общем виде, пользуясь библиотекой символьных вычислений sympy, поэтому дифференцировать будем численно, с помощью функции scipy.misc.derivative:

# для 15 < n < 50
cdf_beta_III_part1 = lambda x: cdf_beta_III(x, θ_1[0], θ_1[1], θ_1[2], θ_1[3], θ_1[4])
pdf_beta_III_part1 = lambda x: sci.misc.derivative(cdf_beta_III_part1, x, dx=1e-6)

# для n >= 50
cdf_beta_III_part2 = lambda x: cdf_beta_III(x, θ_2[0], θ_2[1], θ_2[2], θ_2[3], θ_2[4])
pdf_beta_III_part2 = lambda x: sci.misc.derivative(cdf_beta_III_part2, x, dx=1e-6)

fig, axes = plt.subplots(figsize=(210/INCH, 297/INCH/2))
axes.set_title('Плотность бета-распределения III рода \nпри аппроксимации распределения статистики критерия Эппса-Палли', fontsize=14)
xmin = 0
xmax = 1
x = np.linspace(xmin, xmax, 100)
axes.plot(x, pdf_beta_III_part1(x), label='для 15 < n < 50')
axes.plot(x, pdf_beta_III_part2(x), label='для n >= 50')
axes.legend(loc="best", fontsize=12)
axes.set_xlim(xmin, xmax)
axes.set_xlabel('x')
axes.set_ylabel('pdf_beta_III(x)')

Небольшой Offtop - про тестирование математических расчетов

Самопроверка при выполнении математических расчетов - это, как говорится, основа основ... Ошибиться может каждый. На мой взгляд, лучший способ самопроверки - при выполнении какого-либо тестового расчета выполнить его разными способами, или в разных математических пакетах. Это сильно повышает вероятность отследить ошибки.

В нашем случае, мы выполняем не такие уж сложные расчеты, но с использованием специальных функций и встроенных возможностей python. Функции имеют большое количество параметров, кроме того, в разных математических пакетах методика расчета специальных функций может отличаться. Проверить себя необходимо.

Рассчитаем значение функции бета-распределения III рода для некой условной точки x=0.45, a=0.65, b=0.85 различными способами:

с использованием встроенных возможностей модуля scipy.stat
по определению бета-функции с использованием модуля специальных функций scipy.special (https://docs.scipy.org/doc/scipy/reference/special.html), в котором имеется функция scipy.special.betainc.

Сравним результаты:

# с использованием встроенных возможностей модуля scipy.stat
print(сdf_beta_I(x=0.45, a=0.65, b=0.85))
# с использованием модуля специальных функций scipy.special
print(sci.special.betainc(0.65, 0.85, 0.45))

Как видим, результаты практически совпадают.

Рассчитаем теперь значение плотности бета-распределения III рода для точки x=0.45 в двух вариантах: для 15 < n < 50 и для n >= 50. Эта проверка уже сложнее, так как средствами python мы получили плотность распределения только одним способом - через численное дифференцирование:

print(pdf_beta_III_part1(0.45))
print(pdf_beta_III_part2(0.45))

Второе решение получим с помощью альтернативного математического пакета - системы компьютерной алгебры Maxima. Далее представлен фрагмент программного кода:

Как видим, результаты расчетов также совпадают.

В системе Maxima продублирован полный комплекс расчетов из данного разбора (программный код доступен в моем репозитории на GitHub).

При этом, как я писал выше, мы сталкиваемся с отличием в методике расчетов специальных функций в различных математических пакетах: в системе Maxima неполная бета-функция рассчитывается, в отличие от scipy, без умножения на множитель

В общем, будьте бдительны, товарищи!

Кстати, о системе компьютерной алгебры Maxima (https://sourceforge.net/projects/maxima/files/), ее возможностях, достоинствах, недостатках можно написать отдельно. Этот математический пакет с открытой лицензией нельзя сказать, что очень сильно распространен, хотя о нем написано немало книг, статей, методических указаний, и их количество в последние годы растет.

Из своего собственного опыта я абсолютно убежден, что любому специалисту, деятельность которого так или иначе связана с математическими расчетами, владеть какой-либо системой компьютерной алгебры необходимо, а Maxima имеет для этого немало достоинств:

открытая лицензия;
очень большой математический инструментарий;
обширные возможности для символьных вычислений (например, выше было продемонстрировано, как Maxima позволяет путем подстановки получить символьное выражение для рассматриваемой нами выше функции бета-распределения III рода, а затем, продифференцировав ее, получить символьное выражение для плотности распределения);
удобство использования (лучше, чем в Mathlab или Scilab, но хуже, чем в Mathcad);
компактность кода (одна страница кода в Maxima гораздо информативней, чем, например, в Scilab);
встроенный язык программирования.

Среди недостатков можно отметить:

низкое быстродействие;
необходимость адаптироваться к несколько специфическому синтаксису (например, в Maxima вместо символа операции присваивания значения переменной "=" используется ":");
неприспособленность для решения задач высокой размерности (при решении отдельных задач прикладной статистики с объемами выборки в несколько сотен Maxima начинает вполне ощутимо "тормозить", а при объеме данных в нескольких тысяч - Maxima лучше не применять вовсе).

По-моему личному мнению, Maxima прекрасно подходит как средство тестирования математических расчетов. Впрочем, каждый исследователь сам выбирает для себя инструменты по душе.

Ну, подробнее об этом, напишем отдельно, в другой раз, а пока вернемся к нашей задаче.

6. Проверка гипотезы о нормальности распределения по критерию Эппса-Палли

Проверка гипотезы на основании расчетного и табличного значения статистики критерия:

DecPlace = 5    # точность вывода

print(f'Расчетное значение статистики критерия Эппса-Палли: TEP_calc = {round(TEP_calc, DecPlace)}')

TEP_table = Tep_table(N, p_level=0.95)
print(f'Табличное значение статистики критерия Эппса-Палли: TEP_table = {round(TEP_table, DecPlace)}')

if TEP_calc <= TEP_table:
        conclusion_EP_test = f"Так как TEP_calc = {round(TEP_calc, DecPlace)} <= TEP_table = {round(TEP_table, DecPlace)}" + \
            ", то гипотеза о нормальности распределения по критерию Эппса-Палли ПРИНИМАЕТСЯ"
else:
    conclusion_EP_test = f"Так как TEP_calc = {round(TEP_calc, DecPlace)} > TEP_table = {round(TEP_table, DecPlace)}" + \
            ", то гипотеза о нормальности распределения по критерию Эппса-Палли ОТВЕРГАЕТСЯ"
    
print(conclusion_EP_test)

Проверка гипотезы на основании расчетного и заданного уровня значимости:

if 15 < N < 50:
    a_TEP_calc = 1 - cdf_beta_III(TEP_calc, θ_1[0], θ_1[1], θ_1[2], θ_1[3], θ_1[4])
elif N >= 50:
    a_TEP_calc = 1 - cdf_beta_III(TEP_calc, θ_2[0], θ_2[1], θ_2[2], θ_2[3], θ_2[4])    
print(f'Расчетное (достигнутое) значение уровня значимости: a_TEP_calc = {round(a_TEP_calc, DecPlace)}')

print(f'Заданное значение уровня значимости: a_level = {round(a_level, DecPlace)}')

if a_TEP_calc > a_level:
        conclusion_EP_test = f"Так как a_calc = {round(a_TEP_calc, DecPlace)} > a_level = {round(a_level, DecPlace)}" + \
            ", то гипотеза о нормальности распределения по критерию Эппса-Палли ПРИНИМАЕТСЯ"
else:
    conclusion_EP_test = f"Так как a_calc = {round(a_TEP_calc, DecPlace)} <= a_level = {round(a_level, DecPlace)}" + \
            ", то гипотеза о нормальности распределения по критерию Эппса-Палли ОТВЕРГАЕТСЯ"

print(conclusion_EP_test)

Видим, что расчетное значение уровня значимости a_TEP_calc = 0.75339 практически совпадает с примером в первоисточнике ([3, с.143]): 0.734.

Создание пользовательской функции для реализации теста Эппса-Палли

Для практической работы целесообразно все вышеприведенные расчеты реализовать в виде пользовательской функции Epps_Pulley_test.

Данная функция выводят результаты анализа в виде DataFrame, что удобно для визуального восприятия и дальнейшего использования результатов анализа (впрочем, способ вывода - на усмотрение каждого исследователя).

def Epps_Pulley_test(data, p_level=0.95):
    a_level = 1 - p_level
    X = np.array(data)
    N = len(X)
    
    # аппроксимация предельных распределений статистики критерия
    сdf_beta_I = lambda x, a, b: sci.stats.beta.cdf(x, a, b, loc=0, scale=1)
    g_beta_III = lambda z, δ: δ*z / (1+(δ-1)*z)
    cdf_beta_III = lambda x, θ0, θ1, θ2, θ3, θ4: сdf_beta_I(g_beta_III((x - θ4)/θ3, θ2), θ0, θ1)
    # набор параметров распределения
    θ_1 = (1.8645, 2.5155, 5.8256, 0.9216, 0.0008)    # для 15 < n < 50
    θ_2 = (1.7669, 2.1668, 6.7594, 0.91, 0.0016)    # для n >= 50
    
    if N >= 8:
        # среднее арифметическое
        X_mean = X.mean()
        # центральный момент 2-го порядка
        m2 = np.var(X, ddof = 0)
        # расчетное значение статистики критерия
        A = sqrt(2) * np.sum([exp(-(X[i] - X_mean)**2 / (4*m2)) for i in range(N)])
        B = 2/N * np.sum(
            [np.sum([exp(-(X[j] - X[k])**2 / (2*m2)) for j in range(0, k)]) 
             for k in range(1, N)])
        s_calc_EP = 1 + N / sqrt(3) + B - A
        # табличное значение статистики критерия
        Tep_table_df = pd.read_csv(
            filepath_or_buffer='table/Tep_table.csv',
            sep=';',
            index_col='n')
        p_level_dict = {
            0.9:   Tep_table_df.columns[0],
            0.95:  Tep_table_df.columns[1],
            0.975: Tep_table_df.columns[2],
            0.99:  Tep_table_df.columns[3]}
        f_lin = sci.interpolate.interp1d(Tep_table_df.index, Tep_table_df[p_level_dict[p_level]])
        s_table_EP = float(f_lin(N))
        # проверка гипотезы
        if 15 < N < 50:
            a_calc_EP = 1 - cdf_beta_III(s_calc_EP, θ_1[0], θ_1[1], θ_1[2], θ_1[3], θ_1[4])
            conclusion_EP = 'gaussian distribution' if a_calc_EP > a_level else 'not gaussian distribution'            
        elif N >= 50:
            a_calc_EP = 1 - cdf_beta_III(s_calc_EP, θ_2[0], θ_2[1], θ_2[2], θ_2[3], θ_2[4])
            conclusion_EP = 'gaussian distribution' if a_calc_EP > a_level else 'not gaussian distribution'            
        else:
            a_calc_EP = ''              
            conclusion_EP = 'gaussian distribution' if s_calc_EP <= s_table_EP else 'not gaussian distribution'            
                
    else:
        s_calc_EP = '-'
        s_table_EP = '-'
        a_calc_EP = '-'
        conclusion_EP = 'count less than 8'
    
    result = pd.DataFrame({
        'test': ('Epps-Pulley test'),
        'p_level': (p_level),
        'a_level': (a_level),
        'a_calc': (a_calc_EP),
        'a_calc >= a_level': (a_calc_EP >= a_level if N > 15 else '-'),
        'statistic': (s_calc_EP),
        'critical_value': (s_table_EP),
        'statistic < critical_value': (s_calc_EP < s_table_EP if N >= 8 else '-'),
        'conclusion': (conclusion_EP)},
        index=[1])  
        
    return result

Epps_Pulley_test(X, p_level=0.95)

Другие примеры

Рассматривая остальные примеры из первоисточника [3] - эксперименты Милликена, Майкельсона и Ньюкомба - получим аналогичные результаты расчетов, совпадающие с данными из первоисточника.

Для примера рассмотрим результаты измерения скорости света, полученные Саймоном Ньюкомбом, (миллионные доли секунды) [3, с.139, табл.5.4]:

X = 24.8 + 10**-3 * np.array([
    28,  26,  33,  24,  34, -44, 27,  16,  40,  -2,
    29,  22,  24,  21,  25,  30,  23,  29,  31,  19,
    24,  20,  36,  32,  36,  28,  25,  21,  28,  29,
    37,  25,  28,  26,  30,  32,  36,  26,  30,  22,
    36,  23,  27,  27,  28,  27,  31,  27,  26,  33,
    26,  32,  32,  24,  39,  28,  24,  25,  32,  25,
    29,  27,  28,  29,  16,  23                
    ])

Выполним предварительную визуализацию:

graph_hist_boxplot_probplot_sns(
    data=X,
    data_min=min(X)*0.9995, data_max=max(X)*1.001,
    graph_inclusion='hbp',
    title_axes='Эксперимент Ньюкомба', title_axes_fontsize=16,
    data_label='Скорость света (миллионные доли секунды)')

Видим, что в выборке присутствуют очевидно аномальные значения (выбросы), искажающие результат.
Гипотеза о нормальном распределении исходных данных ОТВЕРГАЕТСЯ:

Epps_Pulley_test(X, p_level=0.95)

Исключим аномальные значения (выбросы) и повторим процедуру:

mask = (X >= 24.81)
X = X[mask]
print(X)

graph_hist_boxplot_probplot_sns(
    data=X,
    data_min=min(X)*0.9995, data_max=max(X)*1.001,
    graph_inclusion='hbp',
    title_axes='Эксперимент Ньюкомба', title_axes_fontsize=16,
    data_label='Скорость света (миллионные доли секунды)')    
    
Epps_Pulley_test(X, p_level=0.95)

Видим, что после исключения выбросов рассчитанные нами параметры практически совпадают с примером в первоисточнике ([3, с.144]):

расчетное значение уровня значимости: наш результат a_calc = 0.4539, результат в первоисточнике 0.461;
расчетное значение статистики критерия Эппса-Палли: наш результат statistic = 0.1074, результат в первоисточнике 0.1074.

Гипотеза о нормальном распределении исходных данных ПРИНИМАЕТСЯ.

В программном коде в моем репозитории на GitHub (https://github.com/AANazarov/Statistical-methods/tree/master/Epps-Pally test) также разобран пример из ГОСТ Р ИСО 5479-2002 - результаты измерения прочности вискозной нити (в условных единицах) [1, с.14, пример 5].

Итоги

Итак, мы рассмотрели способы реализации критерия Эппса-Палли средствами python, разобрали подход к определению расчетного уровня значимости, который можно использовать при реализации других статистических критериев, отсутствующих в наборе стандартных функций python, также предложены пользовательские функции, уменьшающие размер кода. Кроме того, выполнено тестирование математических расчетов альтернативным способом - в системе компьютерной алгебры Maxima.

Исходный код находится в моем репозитории на GitHub.

Отдельную благодарность хочу выразить профессору Новосибирского государственного технического университета Борису Юрьевичу Лемешко, методические разработки которого использовались при написании данного разбора - за отклик, ответы на вопросы и комментарии, данные по электронной почте.

Литература

1. ГОСТ Р ИСО 5479-2002. Статистические методы. Проверка отклонения распределения вероятностей от нормального распределения.

2. Лемешко Б.Ю. и др. Статистический анализ данных, моделирование и исследование вероятностных закономерностей. Компьютерный подход. - Новосибирск: Изд-во НГТУ, 2011. - 888 с.

3. Лемешко Б.Ю. Критерии проверки отклонения распределения от нормального закона. Руководство по применению. - Новосибирск: Изд-во НГТУ, 2014. - 192 с.

4. Хан Г., Шапиро С. Статистические модели в инженерных задачах / пер. с англ. - М.: Мир, 1969. - 395 с.

5. Айвазян С.А. и др. Прикладная статистика: основы моделирования и первичная обработка данных. - М.: Финансы и статистика, 1983. - 471 с.

6. Джонсон Н.Л. и др. Одномерные непрерывные распределения. В 2-х ч. - Ч.2 / пер. с англ. - М.: БИНОМ. Лаборатория знаний, 2012. - 600 с.

7. Постовалов С.Н. Статистический анализ интервальных наблюдений одномерных непрерывных случайных величин: дис. ... канд.тех.наук 05.13.16. - Новосибирск.гос.тех.ун-т: Новосибирск, 1997. - 188 с.

8. Губарев В.В. Вероятностные модели: Справочник. В 2-х ч. - Ч.1. - Новосиб. электротех. ин-т: Новосибирск, 1992. - 198 с.