Текст является переводом фрагмента книги Think Bayes 2 by Allen B. Downey.

В своем замечательном посте John D. Cook рассказал об индексе Линкольна, который является способом оценки количества ошибок в документе (или программе), путем сравнения количества ошибок, найденных независимо двумя тестировщиками.

Вот то как он описал задачу:

Предположим ваш тестер нашел в программе 20 ошибок. И теперь вы хотите прикинуть сколько в программе всего ошибок на самом деле. Вы точно знаете что в программе как минимум 20 ошибок, и если вы абсолютно уверены в высокой квалификации вашего тестера вы можете предположить что в программе на самом деле где-то около 20 ошибок. Но что если квалификация вашего тестера вызывает сомнения? Возможно в программе сотни ошибок. Как в этом случае вы можете оценить количество ошибок? Увы имея в своем распоряжении только одного тестера ничего больше сделать нельзя. Но если у вас два тестера то у вас есть отличный способ оценить общее количество ошибок даже если квалификация тестеров вызывает сомнения.

Предположим первый тестер нашел 20 ошибок, второй нашел 15 ошибок, и 3 ошибки у обоих тестеров совпадают. Как мы можем оценить общее количество ошибок?

Эта задача напоминает предыдущую задачу о медведях Гризли. Поэтому запишем исходные данные в той же форме:

k10 = 20 - 3
k01 = 15 - 3
k11 = 3

k10 — это число ошибок, найденное только первым тестировщиком, k01 — только вторым, k11 — обоими тестировщиками одновременно т.е. имеется в виду пересечение множеств ошибок, найденных первым и вторым тестировщиками. ( прим. пер‑ка ).

Но в этой конкретной задаче было бы неразумно принять вероятность нахождения ошибки одинаковой для обоих тестировщиков. Поэтому мы определим два параметра p0 для вероятности нахождения ошибки первым тестировщиком и p1 для вероятности нахождения ошибки вторым тестировщиком.

Я продолжу считать что вероятности независимы, что означает что сложность нахождения всех ошибок одинакова. Что в общем-то не очень хорошое предположение, но все же давайте пока будем его придерживаться.

Для примера положим мы знаем что вероятности 0.2 и 0.15.

p0, p1 = 0.2, 0.15

Мы можем вычислить массив вероятностей, y:

def compute_probs(p0, p1):
    """Computes the probability for each of 4 categories."""
    q0 = 1-p0
    q1 = 1-p1
    return [q0*q1, q0*p1, p0*q1, p0*p1]

y = compute_probs(p0, p1)
y

[0.68, 0.12, 0.17, 0.03]

Теперь мы можем сказать, что существует шанс вероятностью 68%, что ни один из тестировщиков не найдет ошибку. И шанс вероятностью 3%, что оба найдут одну и ту же ошибку.

Считая указанные вероятности известными мы можем вычислить апостериорное распределение числа ошибок N. В качестве априорного распределения выберем равномерное распределение от 32 до 350:

qs = np.arange(32, 350, step=5) 
prior_N = make_uniform(qs, name='N')
prior_N.head(3)

Поместим вероятности в массив, поставив нуль на месте незвестной величины k00:

data = np.array([0, k01, k10, k11])

И теперь получаем функцию правдоподобия для количества ошибок N:

likelihood = prior_N.copy()
observed = data.sum()
x = data.copy()

for N in prior_N.qs:
    x[0] = N - observed
    likelihood[N] = multinomial.pmf(x, N, y)

Чтобы получить апостериорное распределение обычным образом:

posterior_N = prior_N * likelihood
posterior_N.normalize()

0.0003425201572557094

И вот как все это выглядит:

posterior_N.plot(color='C4')

decorate(xlabel='Number of bugs (N)',
         ylabel='PMF',
         title='Posterior marginal distribution of n with known p1, p2')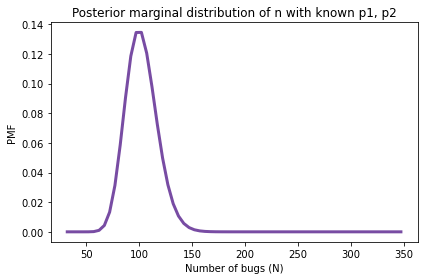

print(posterior_N.mean(), 
      posterior_N.credible_interval(0.9))

102.1249999999998 [ 77. 127.]

В предположении что p0 и p1 равны 0.2 и 0.15, апостериорное среднее 102 с 90% доверительным интервалом (77, 127). Но эти данные получены нами в предположении что мы знаем вероятности, но мы их не знаем.

Трехпараметрическая модель

Нам требуется модель трех параметров N , p0, p1. Мы будем опять использоватьprior_N для априорного распределения числа ошибок N и мы определим априорные распределения для p0 и p1 следующим образом:

qs = np.linspace(0, 1, num=51)
prior_p0 = make_uniform(qs, name='p0')
prior_p1 = make_uniform(qs, name='p1')

Соберем теперь все априорные распределения вместе и получим совместное распределение:

qs = np.linspace(0, 1, num=51)

prior_p0 = make_uniform(qs, name='p0')
prior_p1 = make_uniform(qs, name='p1')

joint2 = make_joint(prior_p0, prior_N)
joint2_pmf = Pmf(joint2.stack())

joint3 = make_joint(prior_p1, joint2_pmf)
joint3_pmf = Pmf(joint3.stack())

Результат это Pmf с трехколоночным MultiIndex содержащим все возможные значения тройки параметров.

Вот похожий на предыдущий цикл вычисления функции правдоподобия:

likelihood = joint3_pmf.copy()
observed = data.sum()
x = data.copy()

for N, p0, p1 in joint3_pmf.index:
    x[0] = N - observed
    y = compute_probs(p0, p1)
    likelihood[N, p0, p1] = multinomial.pmf(x, N, y)

Вычислим апостериорное распределение:

posterior_pmf = joint3_pmf * likelihood
posterior_pmf.normalize()

Теперь получим маргинальные распределения. Вот как мы получим распределение для числа ошибок N:

posterior_N = posterior_pmf.marginal(0)
posterior_N.plot(color='C4')

decorate(xlabel='Number of bugs (N)',
         ylabel='PDF',
         title='Posterior marginal distributions of N')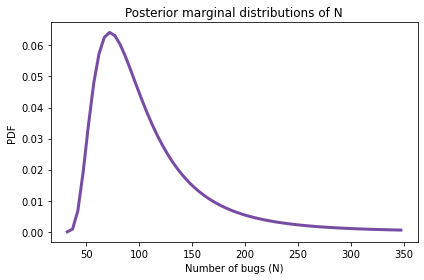

posterior_N.mean()

105.7656173219623

Апостериорное среднее равно 106. Что говорит нам о том, что тестировщики нашли далеко не все ошибки.

Получим теперь апостериорные распределения для p0 и p1:

posterior_p1 = posterior_pmf.marginal(1)
posterior_p2 = posterior_pmf.marginal(2)

posterior_p1.plot(label='p1')
posterior_p2.plot(label='p2')

decorate(xlabel='Probability of finding a bug',
         ylabel='PDF',
         title='Posterior marginal distributions of p1 and p2')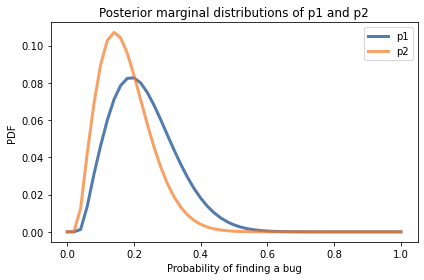

Сравнивая распределения можно сказать что тестер, нашедший больше ошибок, скорее всего должен иметь большую вероятность нахождения ошибок. Но как видно из графиков распределения пересекаются, поэтому мы не можем быть в этом уверены.

Выше был продемонстрирован пример использования трехпараметрической модели. Надо отметить что с увеличением количества параметров возрастает количество комбинаций значений параметров и показанный метод становится непрактичным уже при числе параметров большем 3-4.