Введение

В этой статье представлен простой алгоритм автоматического сшивания нескольких фотографий в плоское (иногда называют перспективное) панорамное изображение (planar/perspective panoramic image). Статья содержит код на языкеPythonс использованием библиотекиOpenCV.

Для построения плоской панорамы требуются изображения снятые из одной точки. То есть камеру можно поворачивать вокруг входного зрачка объектива, но нельзя перемещать. На практике небольшие перемещения не страшны, но они дадут небольшие искажения в итоговом изображении.

Плоская панорама не может охватить область больше по вертикали, горизонтали или другому диаметру (в отличие от панорамных изображений в сферической, цилиндрической и некоторых других проекциях). Но при этом плоская панорама оставляет прямые линии прямыми — мы получим такое изображение, какое получилось бы при съемке с той же точки камерой с бо́льшими углами обзора (меньшим фокусным расстоянием).

Теория

Для начала, нам понадобится вещественная проективная . Проективная плоскость состоит из конечных точек, вида и идеальных точек, вида . Точка не задаёт элемент . На заданы классы эквивалентности — если домножить однородные координаты на ненулевой множитель, то они будут задавать ту же точку в . То есть .

Элементы проективной плоскости можно воспринимать как конечные точкина плоскости , дополненные идеальными точками — точками на бесконечности в направлении . Также элементы проективной плоскости можно воспринимать как линии на плоскости . Во всех теоремах о проективной плоскости работает принцип двойственности, когда можно поменять местами точки и линии и получить двойственную теорему.

также можно представить как множество лучей (хотя точнее будет сказать прямых), вложенных в и проходящих через начало координат. Лучи, пересекающие плоскость , соответствуют конечным точкам , а лучи в плоскости — идеальным.

Гомография (проективное преобразование) — это преобразование которое прямые переводит в прямые. Для нас важно, что гомография задаётся умножением однородных координат на обратимую матрицу . Обратите внимание, что гомография задаёт одно и то же преобразование для всех ненулевых множителей .

Давайте вспомним, как работает модель пинхол камеры. Она задаёт то, как 3D-точка проецируется в точку на плоскости изображения:

В эту же точку проецируются все точки на луче . То есть модель камеры сопоставляет 2D-точку в плоскости изображения лучу в 3D пространстве.

В мы сопоставляем точке в плоскости луч (прямую) . То есть отождествление точки на плоскости с лучём в 3D уже подразумевается и само по себе "проецирование" уже произошло. Для того, чтобы соответствовать модели пинхол камеры, осталось сделать растяжение и смещение плоскости. Это можно сделать следующей гомографией:





Давайте проверим. Пусть у нас задана точка . "Спроецируем" её на плоскость изображения с помощью гомографии .
. То же самое, что предполагается моделью камеры.

Кроме операции проецирования нам интересна операция поворота в 3D. Поворот в 3D задаётся обратимой матрицей . Эта же матрица является матрицей гомографии в и работает точно так же. Только теперь уже на элементах . То есть вращает не точки в , а лучи (прямые).

Применение теории к задаче построения плоской панорамы

У нас есть изображений снятых из одной точки. Будем считать для всех кадров что сьемка велась из начала координат. Матрицы задают поворот каждой камеры. Матрицы задают операцию проецирования каждой камеры. Эти матрицы нам неизвестны.

Рассмотрим произвольную точку нашей 3D-сцены и два кадра и . Обратите внимание, когда мы воспринимаем точку, как элемент , мы работаем с лучом. То есть теряем информацию о положении точки вдоль луча.

В кадрах и проекция точки будет в точках и . Так как матрицы гомографии обратимы, мы можем выразить точку (луч) из первого уравнения:

И подставить во второе:

Обозначим и получим . То есть проекции 3D-точки в кадрах и связаны некоторой гомографией . Так как мы брали точку произвольно, для этих двух изображений эта связь будет работать для всех 3D-точек сцены.

Если мы сможем в кадрах и найти набор 2D-2D соответствий (то есть пары 2D-точек, которые соответствуют одной 3D-точке), то у нас получится набор линейных уравнений вида
, где — матрица из 9 неизвестных чисел (с точностью до ненулевого множителя). Это можно сделать с помощью алгоритма DLT. Таким образом мы получим гомографию, которая переводит точки изображения в точки изображения .

После того, как для пары изображений посчитана гомография, переводящая точки одного изображения в точки другого, мы можем применить её ко всему изображению. Таким образом мы переведём одно изображение в плоскость другого.

Общий алгоритм

Для построения плоской панорамы нам нужно объединить все исходные изображения в одной плоскости. Для упрощения нашего алгоритма будем использовать плоскость первого изображения.

Первое изображение можно преобразовать само в себя с помощью identity гомографии . Для каждого из остальных изображений требуется найти гомографию , которая переводит изображение в плоскость первого изображения. Это не всегда получится сделать. В худшем случае наша панорама будет состоять только из первого изображения.

После нахождения гомографий, когда у нас есть набор изображений и соответствующие им матрицы гомографии, мы можем вычислить границы панорамного изображения и объединить исходные фотографии в одно изображение.

import cv2
import numpy as np
from typing import Tuple, List, Optional

# for type hints
RgbImg = np.array                   # shape = (h, w, 3)
Point2dList = np.array              # shape = (N, 2)
DescriptorsList = np.array          # shape = (N, DESCRIPTOR_SIZE)
HMat = np.array                     # shape = (3, 3)
BBox = Tuple[int, int, int, int]    # BoundingBox(x, y, right, top)


def build_panoramic_image(imgs: List[RgbImg]) -> RgbImg:
    used_imgs: List[Tuple[RgbImg, HMat]] = _find_all_homography(imgs)
    result_bbox: BBox = _get_result_panorama_bbox(used_imgs)
    return _join_panoramic_image(used_imgs, result_bbox)

Поиск 2D-2D соответствий

Для вычисления гомографии между двумя изображениями нам требуется найти 2D-2D соответствия между ними. То есть набор из пар 2D-точек из первого и второго изображения, таких что каждая пара, как мы предполагаем, соответствуют какой-то 3D-точке сцены, изображенной на фотографиях.

Существует много способов получить 2D-2D соответствия. Здесь мы будем использовать детектор локальных особенностей SIFT. Детекторы локальных особенностей принимают на вход изображение и возвращают набор из найденных ключевых точек и их дескрипторов. В случае SIFT дескриптором будет вектор из 128 чисел типа float.

После того как ключевые точки и дескрипторы найдены на обоих изображениях, между ними ищутся соответствия. Это делается с использованием дескрипторов. Если дескрипторы двух точек на разных изображениях близки (по расстоянию), то они, вероятно, соответствуют одной и той же 3D-точке сцены.

В простой реализации можно для каждого дескриптора первого изображения искать ближайший (по расстоянию) дескриптор из второго изображения. Этот алгоритм называется Nearest Neighbour (NN). Мы будем использовать чуть более сложный алгоритм — First-to-Second NN Ratio Check (SNN). Он чуть сложнее, но показывает заметно лучшие результаты. В нём для каждого дескриптора первого изображения ищутся два ближайших дескриптора из второго изображения и проверяется соотношение расстояний до них. Если оно близко к единице (то есть второй ближайший дескриптор второго изображения находится примерно на таком же расстоянии от дескриптора первого изображения как первый), то это соответствие считается плохим. Если соотношение меньше , то это соответствие можно использовать.

def _detect_sift_points_and_descriptors(img: RgbImg) -> \
        Tuple[Point2dList, DescriptorsList]:
    img_gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
    sift = cv2.SIFT_create()
    keypoints, descriptors = sift.detectAndCompute(img_gray, None)
    return np.array([kp.pt for kp in keypoints]), descriptors


def _snn_matching(query_descriptors: DescriptorsList,
                  train_descriptors: DescriptorsList) -> List[cv2.DMatch]:
    matcher = cv2.BFMatcher_create(cv2.NORM_L2, False)
    matches_all = matcher.knnMatch(query_descriptors, train_descriptors, 2)
    return [m1 for m1, m2 in matches_all if m1.distance < 0.8 * m2.distance]


def _find_matches(points1: Point2dList, descriptors1: DescriptorsList,
                  points2: Point2dList, descriptors2: DescriptorsList) -> \
        Tuple[Point2dList, Point2dList]:
    matches = _snn_matching(descriptors1, descriptors2)
    return np.array([points1[m.queryIdx] for m in matches]), \
           np.array([points2[m.trainIdx] for m in matches])

Вычисление матриц гомографии

По найденным 2D-2D соответствиям можно найти матрицу гомографии. Для этого используется алгоритм Direct Linear Transform (DLT).

Не все 2D-2D соответствия являются верными. Часть из них (обычно бо́льшая часть) — выбросы, которые будут "тянуть" решение в неправильную сторону, если считать матрицу гомографии напрямую по всем 2D-2D соответствиям. Для отсеивания выбросов можно использовать алгоритм RANSAC. К счастью, алгоритм поиска матрицы гомографии, использующий RANSAC, уже реализован в библиотеке OpenCV.

В результате мы найдём матрицу гомографии, которая переводит плоскость изображения 2 в плоскость изображения 1. Если 2D-2D соответствий недостаточно, то вернём None и проигнорируем это изображение. В более сложных алгоритмах можно сопоставлять локальные особенности между всеми изображениями, а не только с первым. Такой подход поможет использовать изображения, не пересекающиеся с первым и повысить качество. Для простого алгоритма построения панорамы нашей реализации будет достаточно.

def _find_homography(points1: Point2dList, points2: Point2dList) -> \
        Optional[HMat]:
    _MIN_MATCHES, _MIN_INLIERS = 100, 30
    if len(points1) < _MIN_MATCHES:
        return None
    hmat, inliers_mask = cv2.findHomography(points2, points1, cv2.RANSAC)
    return hmat if np.sum(inliers_mask) >= _MIN_INLIERS else None


def _find_all_homography(imgs: List[RgbImg]) -> List[Tuple[RgbImg, HMat]]:
    first_img = imgs[0]
    result = [(first_img, np.eye(3))]
    points1, descriptors1 = _detect_sift_points_and_descriptors(first_img)
    for img in imgs[1:]:
        points, descriptors = _detect_sift_points_and_descriptors(img)
        matches = _find_matches(points1, descriptors1, points, descriptors)
        hmat = _find_homography(matches[0], matches[1])
        if hmat is not None:
            result.append((img, hmat))
    return result

Вычисление границ панорамного изображения

Перед тем как объединять все изображения в одно, нам нужно узнать размер итогового изображения.

У нас есть набор изображений и набор матриц гомографии, которые переводят все изображения в одну плоскость. Давайте найдём прямоугольник, ограничивающий все изображения в результирующей плоскости.

Так как изображение это прямоугольник, а гомография все линии переводит в линии, то в целевой плоскости изображение превратится в четырёхугольник. Соответственно, мы можем применить гомографию ко всем углам всех изображений и посчитать ограничивающий их прямоугольник.

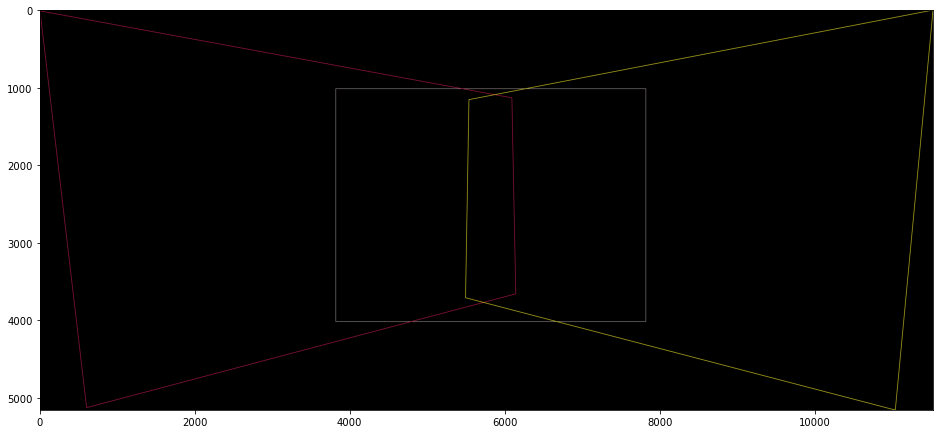
Такой алгоритм будет работать во всех случаях, кроме тех, когда какая то из точек изображения переводится в бесконечность. Это может произойти, если в каком то из направлений (относительно оптического центра панорамы) угловой размер превысит . Проигнорируем этот случай в нашем алгоритме.

Ещё одна важная деталь. Даже если до бесконечности мы не дошли, всё равно итоговый размер панорамы может получиться сколь угодно большим. Давайте ограничим его некоторой константой. Например, пусть размер панорамы будет не больше нескольких диаметров первого изображения.

def _get_transformed_img_bbox(img: RgbImg, hmat: HMat) -> BBox:
    h, w = img.shape[:2]
    corners = np.float32([[0, 0], [0, h], [w, h], [w, 0]]).reshape(-1, 1, 2)
    corners = cv2.perspectiveTransform(corners, hmat).reshape(-1, 2)
    return np.min(corners[:, 0]), np.min(corners[:, 1]), \
           np.max(corners[:, 0]), np.max(corners[:, 1])


def _max_panoramic_image_bbox(first_image: RgbImg) -> BBox:
    _MAX_SIZE_DIAMETERS = 2.0
    h, w = first_image.shape[:2]
    sz = int(_MAX_SIZE_DIAMETERS * np.linalg.norm((w, h)))
    return -sz, -sz, w + sz, h + sz


def _get_result_panorama_bbox(used_imgs: List[Tuple[RgbImg, HMat]]) -> BBox:
    x, y, r, t = 0.0, 0.0, 0.0, 0.0
    for img, hmat in used_imgs:
        i_x, i_y, i_r, i_t = _get_transformed_img_bbox(img, hmat)
        x, y, r, t = min(x, i_x), min(y, i_y), max(r, i_r), max(t, i_t)
    x, y, r, t = int(x), int(y), int(r), int(t)

    min_x, min_y, max_r, max_t = _max_panoramic_image_bbox(used_imgs[0][0])
    return max(x, min_x), max(y, min_y), min(r, max_r), min(t, max_t)

Сшивание плоской панорамы

Теперь дело за малым — нужно объединить все изображения в одно. Для того, чтобы применить гомографию ко всему изображению, можно воспользоваться функцией warpPerspective из OpenCV. Она делает тоже самое, что мы делали для углов изображения, но для всех пикселей и с интерполяцией.

В самой простой реализации можно применить гомографии ко всем изображениям, чтобы получить изображения в одной плоскости. И потом усреднить все цвета. Этот алгоритм даёт не лучшие результаты, но для наших целей он подойдёт.

def _join_panoramic_image(used_imgs: List[Tuple[RgbImg, HMat]],
                          result_bbox: BBox) -> RgbImg:
    offset_hmat = np.array([[1, 0, -result_bbox[0]],
                            [0, 1, -result_bbox[1]],
                            [0, 0, 1]])

    result_w = result_bbox[2] - result_bbox[0]
    result_h = result_bbox[3] - result_bbox[1]

    sum_rgb = np.zeros((result_h, result_w, 3))
    sum_mask = np.zeros((result_h, result_w))
    for img, hmat in used_imgs:
        warped_img = cv2.warpPerspective(
            img, offset_hmat @ hmat, (result_w, result_h))
        mask = np.sum(warped_img, axis=2) != 0
        mask = cv2.erode(mask.astype(sum_mask.dtype), np.ones((3, 3)))
        sum_rgb[mask != 0] += warped_img[mask != 0]
        sum_mask += mask

    sum_rgb[sum_mask != 0] /= sum_mask[sum_mask != 0][:, None]
    return sum_rgb.astype(np.uint8)

Заключение

Мы разобрали простой алгоритм автоматического построения плоского панорамного изображения. В процессе мы затронули большое количество разных алгоритмов и терминов, использующихся в компьютерном зрении.

Представленный алгоритм не рекомендуется использовать на практике. Но он достаточно компактен и подходит для изучения и экспериментов с детекторами локальных особенностей, матрицами гомографий и т.д.

Что используется в полноценных решениях, чего в нашем простом алгоритме нет?

Есть много вещей, которые могли бы улучшить решение. Например, компенсация дисторсии в исходных изображениях, более интеллектуальный поиск 2D-2D соответствий (например, построение графа из изображений) или использование более продвинутых алгоритмов слияния изображений (например Multiband blending).

Самое главное отличие нашего алгоритма от более продвинутых — в них поиск матриц гомографии лишь один из этапов. После чего происходит восстановление матриц поворота и проекции для каждого изображения (матрицы проекции часто считаются одинаковыми для всех камер или, даже, известными). Такой подход позволяет строить любую панораму, а не только плоскую. Если для камеры известны , то для каждой точки изображения известен соответствующий ей луч. И всё изображение можно спроецировать изнутри на цилиндр, чтобы получить цилиндрическую панораму, сферу, для сферической панорамы, и т.д. Даже для плоской панорамы такой подход тоже имеет свои плюсы. Можно вычислить направление вокруг которого сосредоточено максимальное количество данных изображений, и центрировать плоскость относительно него. Да и матрицы гомографии получаются точнее, при восстановлении их из вместо поиска в произвольном виде. Например, при известных параметрах камеры, каждая гомография задаётся матрицей поворота. Это 3 степени свободы вместо 8 в общем случае.

Материалы

1. Multiple View Geometry in Computer Vision. Richard Hartley and Andrew Zisserman — одна из фундаментальных книг классического компьютерного зрения. Содержит всю теорию, использовавшуюся в данной статье;

2. Автоматическое построение плоской панорамы — исходный код реализованного в статье алгоритма;

3. Модель камеры — подробная статья о модели пинхол камеры;

4. Hugin — инструмент для сшивания панорамных изображений с открытым исходным кодом;

5. Image Composite Editor — бесплатный инструмент для сшивания панорамных изображений от Microsoft.