Читателю не столь хорошо знакомому с теоретической информатикой может показаться удивительным, что нижние оценки известны лишь для малого числа задач. Когда оценивают сложность алгоритма, используют -нотацию — асимптотически верхнюю оценку на сложность алгоритма. Так, хорошо известно, что у сортировки слиянием сложность Из теории известно, что ни одна сортировка сравнениями не может сортировать асимптотически лучше чем за (пишут ), отсюда для сортировки слиянием берётся нижняя оценка. Верхняя оценка сложности алгоритма, решающего задачу, является и верхней оценкой сложности самой задачи, поэтому сортировки сравнениями имеют точную асимптотическую оценку .

Большинство нижних оценок имеют вид , где традиционно длина входа. Увы, наука чаще всего умеет доказывать только простые вещи в духе «для решения задачи необходимо считать весь вход». Даже для сортировок не ограниченных только доступом к сравнениям нижняя оценка остаётся открытым вопросом (при дополнительных ограничениях на вход за линейное время работает, например, Counting Sort). Чаще всего во вводных курсах по алгоритмам и книжках можно встретить нижние оценки для задач на взвешивание: поиск максимума за сравнение, одновременный поиск максимума и минимума за сравнений, и ещё несколько подобных задач. За исключением нескольких простых хорошо известных примеров, задачи на нижние оценки часто оказываются либо сложными, либо требуют знакомство со специальной (математической) техникой, нужной для их решения. Какого же было моё удивление, когда я встретил среди задач, используемых на вступительных испытаниях в Школу анализа данных Яндекса задачу на нижние оценки, которую можно решить достаточно простым способом!

Эта задача оказалась связана с одним из моих любимых сюжетов о структурах данных, который редко встречается из-за отсутствия практической значимости. Речь о таблицах Юнга (Young tableau), которые встречаются в качестве задачи в Кормене. Представьте, что у вас есть таблица (матрица) , элементы которой подчиняются следующему свойству: при и (одновременно). На рисунке ниже приведён пример таблицы Юнга, в качестве направлений осей координат мы выбрали «вправо» и «вверх» (точка 0,0 в левом нижнем углу).

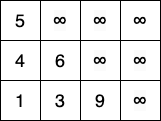
Если разрешить в качестве элемента хранить ещё и договориться, что бесконечность означает свободное место, то на эту таблицу можно смотреть как на структуру данных: в неё можно добавлять элементы (если есть место), удалять элементы, и проверять, входит ли элемент в таблицу. Более того, её можно использовать и как структуру на минимум! Минимум находится в левом нижнем углу. В общем, таблица Юнга отличная структура данных, которую можно использовать, например, при обучении школьников информатике, но на практике она не годится из-за медленного времени работы по сравнению со сбалансированными двоичными деревьями поиска. Перечисленные выше операции выполняются за время , где число столбцов, а число строк. Таким образом, полностью заполненная квадратная таблица Юнга содержит элементов, а сложность запроса тогда . Придумать алгоритмы, реализующие перечиселенные операции предлагается в Кормене в качестве задачи. Мы обсудим только алгоритм проверки вхождения числа в таблицу (который также встречается в книге А. Шеня «Программирование: теоремы и задачи») и докажем нижнюю оценку на проверку вхождения: что нельзя найти число в таблице (или убедиться, что его нет), узнав содержимое меньше чем клеток. Если хотите сначала попробовать решить эти задачи самостоятельно, не переходите к следующему абзацу.

Как обычно построение алгоритма, (почти) достигающего нижнюю оценку помогает лучше почувствовать задачу. Обратим внимание на ячейку таблицы в левом верхнем угле (её наш алгоритм запросит первой). Пусть в ней стоит число . Если , то мы нашли искомое вхождение и задача решена; при получаем, что во всей верхней строке числа не меньше , поэтому там встретиться не может, а при получаем, что в левом столбце все числа меньше и в нём тоже встретиться не может. Таким образом, в зависимости от мы либо найдём , либо исключим из поисков строку или столбец таблицы. Мысленно вычеркнем исключенную строку (или столбец) и повторим процедуру: посмотрим в получившейся таблице на левый верхний угол. С каждым шагом этой процедуры мы исключаем строку или столбец, а потому таких действий не больше чем .

Перейдём теперь к нижней оценке. Напомним, что оценивая сложность алгоритма мы оцениваем число операций в худшем случае (на входе длины ). Также мы пользуемся детерминированностью алгоритма: каждый следующий шаг алгоритма зависит только от предыдущих шагов и не может зависеть, например, от информации, которую алгоритм ещё не получил. Представим, что , и построим следующую частично-заполненную таблицу Юнга: диагональ, ведущая из левого верхнего угла, не заполена, ниже неё стоят единицы, а выше — тройки.

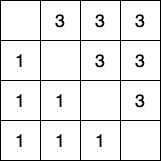
Заметьте, что в любой клетке диагонали может стоять любое из чисел 1, 2 или 3, и это число никак не влияет на другие числа на диагонали. Докажем, что любой алгоритм, решающий задачу, обязан спросить все клетки диагонали (в случае входа такого вида). Представим, что мы играем с алгоритмом в игру: алгоритм спрашивает нас клетку, мы сообщаем её содержимое; в результате наших ответов должна получится корректная таблица Юнга (если потом потребуется показать оставшиеся клетки). Если алгоритм спрашивает какую-то клетку вне диагонали, то он получает 1 или 3 в зависимости от положения клетки. Когда алгоритм спрашивает клетку на диагонали, мы будем отвечать 1. Таким образом, если алгоритм не спросил про все клетки на диагонали, то там может оказаться 2. Но если алгоритм заявит, что в этой клетке находится двойка, то мы можем подать ему на вход другую таблицу, в которой вместо 2 стоит 3; в силу детерминизма алгоритм задаст те же вопросы, получит те же ответы и сообщит, что 2 стоит на месте 3, что неверно — такой алгоритм не может решить задачу! Итак, мы доказали, что для проверки вхождения числа в квадратную таблицу Юнга размера , алгоритмы необходимо совершить хотя бы запросов , поэтому в случае квадратной таблица Юнга операция проверки вхождения имеет сложность .

Автор: Александр Рубцов, к. ф.-м. н., доцент, МФТИ, преподаватель ШАД Хелпер