Какова вероятность найти слово fuck в случайной последовательности из 20 букв? / forpes.ru

Главная
Какова вероятность найти слово fuck в случайной последовательности из 20 букв?

Какова вероятность найти слово fuck в случайной последовательности из 20 букв? +43

26.11.2023 20:09

ibessonov 79 8800 Источник

Однажды на работе возник вопрос — насколько вероятно, что в случайно сгенерированном идентификаторе (отдаваемом пользователю, к примеру) вдруг обнаружится плохое слово. Приблизительная оценка была дана достаточно быстро, а вот точное решение — уже не так тривиально.

Я решил всерьёз выяснить, чему равна эта вероятность в зависимости от длины случайной строки? Можно ли получить явную математическую формулу для ответа? Что, если взять другое слово? Что, если взять другой алфавит?

Обо всём по порядку.

1. Метод Монте-Карло

Что может быть легче? Генерируем миллионы — миллиарды! — случайных строк и проверяем, содержат ли они искомое слово.
Метод очень прост в реализации. Программа, перебирающая случайные строки в течение 30 секунд, для параметров из заголовка выдала ответ примерно $inline$ . Позже мы увидим, насколько он близок к точному значению.

Тут есть проблема, которая должна быть очевидна: метод Монте-Карло по времени вычисления является самым затратным из описанных в статье и сходится очень медленно. Это особенно хорошо видно, когда нужно получить точность порядка 8-9 знаков после запятой.
Зачем такая точность, спрашиваете? Чтобы была!

На задачи обозначенного размера даже 30 миллисекунд процессорного времени тратить не хочется, не то что просто секунд. Решение, пусть и универсальное, совершенно не годится.

2. Приблизительное решение

Второй вариант, который приходит на ум: быстро подобрать простую формулу и надеяться на то, что она даст хорошую аппроксимацию.

Вопрос: какой может быть позиция подстроки fuck внутри строки из 20-ти символов? Ответ: от 0 до 16, т.е. 17 различных вариантов. Для каждой такой позиции i, существует $26^{16}$ различных слов, в которых fuck — на i-й позиции (т.е. все возможные комбинации оставшихся 16-ти букв в строке).

Приняв к сведению, что некоторые слова мы посчитаем несколько раз (те, в которых fuck содержится более одного раза), можно сказать, что слов, содержащих fuck, будет точно меньше, чем $17\cdot26^{16}$ , а вероятность, соответственно, не превысит $17\cdot\frac{26^{16}}{26^{20}}$ (в знаменателе — количество всех возможных слов длины 20).

Это значение равно $\frac{17}{456976}$ , или приблизительно $inline$ .

3. Поиск точной формулы

3.1. Рекуррентное соотношение

Все последующие рассуждения будут касаться формул или процедур для получения точного ответа. Очевидно, что подходов может быть множество. Предлагаю начать с простейшей более-менее общей формулировки. Есть английский алфавит из 26 букв, найти количество слов длины $inline$ , содержащих в себе последовательность букв fuck хотя бы один раз.

Обозначим такое количество за $inline$ . Начинается последовательность безобидно:

$display$

Строки короче 4-х символов точно не содержат нужное подслово, а среди строк из 4-х символов есть только один подходящий кандидат — сама строка fuck. Достаточно быстро значения становятся менее упорядоченными:

$C_4(5)=2\cdot26, C_4(6)=3\cdot26^2, C_4(7)=4\cdot26^3, C_4(8)=5\cdot26^4-1, \ldots$

Тут всё ещё видна некая закономерность, но она очень быстро сломается, гарантирую.

Попробуем рассмотреть, как же значение с большими $inline$ зависит от значений с меньшими $inline$ . Допустим, что $inline$ . Предлагаю пересчитывать строки следующим способом:

Если префикс длины $inline$ уже содержит искомое слово, то выбор последней буквы ни на что не влияет, т.е. мы бесплатно получаем $26 \cdot C_4(n - 1)$ строк.
Если строка оканчивается на fuck, то первые $inline$ букв значения не имеют. Итого добавляется ещё $26 ^ {n - 4}$ строк.
Других вариантов быть не может: слово fuck встречается либо в конце, либо не в конце, но есть проблема — часть строк посчитаны дважды. В частности, те, которые оканчиваются на fuck и содержат его более, чем один раз (afuckafuck).
Нетрудно понять, что это единственный вид исключений. И все такие строки обязательно содержат fuck среди первых $inline$ символов, это значение мы и должны отнять как дважды посчитанное.

Итого, объединив все рассуждения, приходим к рекуррентному соотношению:

$C_4(n) = 26 \cdot C_4(n - 1) + 26^{n - 4} - C_4(n - 4)$

Стоит заметить, что с таким же удобством можно было бы рассматривать величины $inline$ , которые являлись бы не количеством, а вероятностью, или, точнее, пропорцией количества искомых строк с количеством всех возможных строк длины $inline$ . В новых терминах формула примет следующий вид. На мой взгляд, стало намного лучше:

$p_4(n) = p_4(n - 1) + \frac{1 - p_4(n - 4)}{26^ 4}$

Код для подобного соотношения будет тривиальным. Ответ для слов длины 20 равен $inline$ . Видно, что реальное значение отличается от ответа, полученного методом Монте-Карло, уже на 7-м знаке после запятой ( $inline$ ), а если отбросить нули, то и вовсе в третьей значащей цифре.
Простая аппроксимация ( $inline$ ) показала себя значительно лучше, дав ошибку лишь в 9-м знаке после запятой (пятой значащей цифре).

Рекуррентная формула — это хорошо, но явная формула — лучше, хочется и её найти.

Помимо этого, сложность процедуры вычисления рекуррентного соотношения является $inline$ , что не является оптимальной трудоёмкостью для данной задачи. Её обязательно нужно понизить.

3.2. Явная формула

На самом деле, задача очень даже типовая. Хорошо известно, как получить явную формулу для подобного класса задач, пусть и совсем не очевидно, почему надо поступать именно так. Но этот вопрос мы опустим, лучше найдём формулу.

В первую очередь забываем о начальном условии $inline$ на какое то время.
Напомню исходную рекуррентную формулу, слегка её обобщив, чтобы она была сейчас перед глазами. За $inline$ я обозначил значение $\frac{1}{26 ^ 4}$ , чтобы не делать последующие выражения ещё более громоздкими.

$p_4(n) = p_4(n - 1) + k - k \cdot p_4(n - 4)$

Для начала нужно найти частное решение, почти как в дифференциальных уравнениях. К счастью, оно лежит на поверхности: $p_4(n) \equiv 1$ . Действительно, подставив $inline$ в уравнение получим, что обе части тождественно равны.

Зная частное решение, само уравнение можно немного упростить. Положим $inline$ и попробуем искать ответ относительно $inline$ :

$q(n) = q(n - 1) - k \cdot q(n - 4)$

Перенеся всё в одну сторону, получим:

$q(n) - q(n - 1) + k \cdot q(n - 4) = 0$

Далее делается знаменитый финт ушами и предполагается, что есть возможность найти решение в виде $q(n) = \mu^n$ для некоего значения $\mu$ . Думаю многим читателям данный финт может быть знаком из вывода общей формулы для членов Фибоначчи, но работает он для любой линейной рекуррентной последовательности. Подставим:

$\mu^n - \mu^{n - 1} + k \cdot \mu^{n - 4} = 0$

Сократив это выражение на $\mu^{n - 4}$ , получим уравнение четвёртой степени:

$\mu^4 - \mu^3 + k = 0$

Это уравнение называется "характеристический многочлен", и у него есть 4 различных корня:

Спасибо, Wolfram|Alpha

Очень надеюсь, что я правильно скопировал ответ:
$\mu_1 = \frac{1}{4} -\frac{1}{2} \sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}\\ -\frac{1}{2} \sqrt{\Bigg(- \frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} - \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}}\\ - \frac{1}{4\sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}} + \frac{1}{2} \Bigg)}$

$\mu_2 = \frac{1}{4} -\frac{1}{2} \sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}\\ +\frac{1}{2} \sqrt{\Bigg(- \frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} - \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}}\\ - \frac{1}{4\sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}} + \frac{1}{2} \Bigg)}$

$\mu_3 = \frac{1}{4} +\frac{1}{2} \sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}\\ -\frac{1}{2} \sqrt{\Bigg(- \frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} - \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}}\\ + \frac{1}{4\sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}} + \frac{1}{2} \Bigg)}$

$\mu_4 = \frac{1}{4} +\frac{1}{2} \sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}\\ +\frac{1}{2} \sqrt{\Bigg(- \frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} - \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}}\\ + \frac{1}{4\sqrt{\frac {4\sqrt[3]{\frac{2}{3}}k} {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} + \frac {\sqrt[3]{\sqrt{3} \sqrt{27k^2-256k^3} + 9k}} {\sqrt[3]{2} \ 3^{2/3}} + \frac{1}{4}}} + \frac{1}{2} \Bigg)}$

Несложно убедиться, что если $q_1(n)=\mu_1^n$ и $q_2(n)=\mu_2^n$ — решения, то и $a \cdot q_1(n) + b \cdot q_2(n)$ — тоже решение, где $inline$ и $inline$ — произвольные константы. Т.е. решение в общем виде выглядит так:

$p_4(n) = a\mu_1^n + b\mu_2^n + c\mu_3^n + d\mu_4^n + 1$

Значения $inline$ , $inline$ , $inline$ и $inline$ следует искать из начальных условий:

$\left\{ \begin{array} &p_4(0) = a &+\ b &+\ c &+\ d &+\ 1 &= 0\\ p_4(1) = a\mu_1 &+\ b\mu_2 &+\ c\mu_3 &+\ d\mu_4 &+\ 1 &= 0\\ p_4(2) = a\mu_1^2 &+\ b\mu_2^2 &+\ c\mu_3^2 &+\ d\mu_4^2 &+\ 1 &= 0\\ p_4(3) = a\mu_1^3 &+\ b\mu_2^3 &+\ c\mu_3^3 &+\ d\mu_4^3 &+\ 1 &= 0\\ \end{array} \right.$

Решаем данную систему и подставляем результат в ответ, всё просто! Для этого воспользуемся методом Крамера, который выражает решения системы линейных уравнений через определители некоторых матриц. Выглядеть матрицы будут следующим образом:

$\Delta=\begin{vmatrix} 1 & 1 & 1 & 1 \\ \mu_1 & \mu_2 & \mu_3 & \mu_4 \\ \mu_1^2 & \mu_2^2 & \mu_3^2 & \mu_4^2 \\ \mu_1^3 & \mu_2^3 & \mu_3^3 & \mu_4^3 \\ \end{vmatrix}$

$\Delta_a=-\begin{vmatrix} 1 & 1 & 1 & 1 \\ 1 & \mu_2 & \mu_3 & \mu_4 \\ 1 & \mu_2^2 & \mu_3^2 & \mu_4^2 \\ 1 & \mu_2^3 & \mu_3^3 & \mu_4^3 \\ \end{vmatrix} \: \Delta_b=-\begin{vmatrix} 1 & 1 & 1 & 1 \\ \mu_1 & 1 & \mu_3 & \mu_4 \\ \mu_1^2 & 1 & \mu_3^2 & \mu_4^2 \\ \mu_1^3 & 1 & \mu_3^3 & \mu_4^3 \\ \end{vmatrix}$

$\Delta_c=-\begin{vmatrix} 1 & 1 & 1 & 1 \\ \mu_1 & \mu_2 & 1 & \mu_4 \\ \mu_1^2 & \mu_2^2 & 1 & \mu_4^2 \\ \mu_1^3 & \mu_2^3 & 1 & \mu_4^3 \\ \end{vmatrix} \Delta_d=-\begin{vmatrix} 1 & 1 & 1 & 1 \\ \mu_1 & \mu_2 & \mu_3 & 1 \\ \mu_1^2 & \mu_2^2 & \mu_3^2 & 1 \\ \mu_1^3 & \mu_2^3 & \mu_3^3 & 1 \\ \end{vmatrix}$

В данных терминах решения будут найдены в виде $a=\frac{\Delta_a}{\Delta}$ , $b=\frac{\Delta_b}{\Delta}$ , $c=\frac{\Delta_c}{\Delta}$ и $d=\frac{\Delta_d}{\Delta}$ .
Можно заметить, что каждый из определителей является определителем Вандермонда, для которого есть замечательная формула вычисления:

$\Delta = \prod\limits_{1\le j < i \le 4}(\mu_i - \mu_j) = (\mu_4 - \mu_3)(\mu_4 - \mu_2)(\mu_4 - \mu_1)(\mu_3 - \mu_2)(\mu_3 - \mu_1)(\mu_2 - \mu_1)$
$\Delta_a = -(\mu_4 - \mu_3)(\mu_4 - \mu_2)(\mu_4 - 1)(\mu_3 - \mu_2)(\mu_3 - 1)(\mu_2 - 1)$
$\Delta_b = -(\mu_4 - \mu_3)(\mu_4 - 1)(\mu_4 - \mu_1)(\mu_3 - 1)(\mu_3 - \mu_1)(1 - \mu_1)$
$\Delta_c = -(\mu_4 - 1)(\mu_4 - \mu_2)(\mu_4 - \mu_1)(1 - \mu_2)(1 - \mu_1)(\mu_2 - \mu_1)$
$\Delta_d = -(1 - \mu_3)(1 - \mu_2)(1 - \mu_1)(\mu_3 - \mu_2)(\mu_3 - \mu_1)(\mu_2 - \mu_1)$

Поделив определители друг на друга, получим симпатичный ответ:

$\left\{ \begin{array} &a=-\frac{(1-\mu_2)(1-\mu_3)(1-\mu_4)}{(\mu_1-\mu_2)(\mu_1-\mu_3)(\mu_1-\mu_4)}\\ b=-\frac{(1-\mu_1)(1-\mu_3)(1-\mu_4)}{(\mu_2-\mu_1)(\mu_2-\mu_3)(\mu_2-\mu_4)}\\ c=-\frac{(1-\mu_1)(1-\mu_2)(1-\mu_4)}{(\mu_3-\mu_1)(\mu_3-\mu_2)(\mu_3-\mu_4)}\\ d=-\frac{(1-\mu_1)(1-\mu_2)(1-\mu_3)}{(\mu_4-\mu_1)(\mu_4-\mu_2)(\mu_4-\mu_3)} \end{array} \right.$

Т.е. $p_4(n)=1 - \frac{\mu_1^n(1-\mu_2)(1-\mu_3)(1-\mu_4)}{(\mu_1-\mu_2)(\mu_1-\mu_3)(\mu_1-\mu_4)} - \frac{\mu_2^n(1-\mu_1)(1-\mu_3)(1-\mu_4)}{(\mu_2-\mu_1)(\mu_2-\mu_3)(\mu_2-\mu_4)}\\ - \frac{\mu_3^n(1-\mu_1)(1-\mu_2)(1-\mu_4)}{(\mu_3-\mu_1)(\mu_3-\mu_2)(\mu_3-\mu_4)} - \frac{\mu_4^n(1-\mu_1)(1-\mu_2)(1-\mu_3)}{(\mu_4-\mu_1)(\mu_4-\mu_2)(\mu_4-\mu_3)}$

4. Поиск эффективной процедуры вычисления

4.1. Регулярный язык

Данный конкретный случай со словом длиной 4 решён в явном виде. Но, помимо математической красоты, практической ценности он не имеет. При словах длиной больше, чем 4, степень характеристического многочлена будет увеличиваться. Так как уравнения степени выше четвёртой не имеют формулы для их решения, то с нахождением соответствующих значений $\mu$ могут возникнуть серьёзные проблемы (хотя Wolfram|Alpha и способен выдать решения соответствующего уравнения 5-й степени через обобщённые гипергеометрические функции, я понятия не имею, что это такое). Конечно, можно попробовать решать их численно, но это как-то слишком сложно для такой простой задачи.

К слову, пусть и не всегда можно явно вычислить корни характеристического многочлена, все рассуждения можно почти дословно повторить для всех $p_m(n) = p_m(n - 1) + k - k \cdot p_m(n - m)$ , соответствующих "простым" искомым словам длины $inline$ . Что я имею ввиду под "простыми" словами, будет объяснено ближе к концу статьи, не всё сразу.

Не думаю, что можно выжать ещё какие-то интересные факты из решения с помощью рекуррентной формулы, так что будем использовать другой подход. К математике вернёмся попозже.

Поговорим о регулярных языках. Строки, содержащие подстроку fuck, описываются регулярным выражением ^.*fuck.*$ (пользуясь синтаксисом для языка Java). Эквивалентный способ описания регулярных языков, на практике менее привычный — это конечные автоматы. В частности, детерминированные конечные автоматы (ДКА). Они сложнее в построении, но проще в обработке. ДКА для описания языка, все слова которого содержат подслово fuck, выглядит следующим образом:

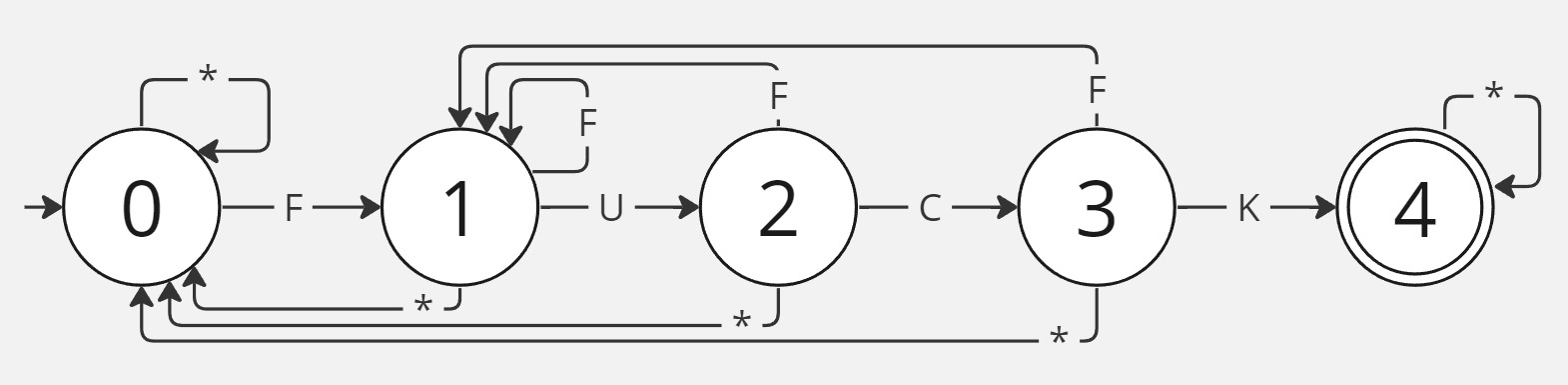
Переходы, помеченные звёздочкой, фактически означают "ветку else" — все оставшиеся символы, которые не встречаются в явно помеченных переходах.

Состояние $inline$ — начальное, $inline$ — завершающее, все остальные — промежуточные. Видно, что данный конечный автомат не только детерминированный, но и полный, т.е. для каждого состояния и каждого символа алфавита определена функция перехода (существует выходящее ребро графа с соответствующей меткой). Это важно и понадобится в будущем.

Наделим состояния автомата осязаемым смыслом, начиная с последнего.

$inline$ — на текущий момент уже найдено подслово fuck и все оставшиеся символы просто пропускаются с помощью перехода из завершающего состояния в него же.
$inline$ — на текущий момент прочитан префикс, заканчивающийся на fuc. Есть два возможных варианта — либо дальше идёт k и можно переходить в завершающее состояние, либо там другой символ и поиск нужно "начинать сначала", т.е. идти либо в $inline$ если увидели f, либо идти вообще в начальное состояние $inline$ .
$inline$ — на текущий момент прочитан префикс, заканчивающийся на fu. Есть два возможных варианты — либо дальше идёт символ c, удлиняющий текущий найденный префикс слова fuck, либо какой-то другой символ, не позволяющий увеличить прочитанный префикс и заставляющий нас идти либо в $inline$ , либо в $inline$ .
...

Не хочется ещё несколько раз повторять ту же самую идею. Важно вот что — состояние $inline$ означает, что в момент нахождения в нём мы уже вычитали префикс, совпадающий с префиксом длины $inline$ строки fuck.

Далее я предлагаю отождествлять префиксы искомого слова с названиями состояний соответствующего конечного автомата. Перерисую его с учётом новых названий:

Как по конечному автомату понять, сколько слов длины $inline$ он сможет распознать? В общем случае этот вопрос может показаться сложным, но точно не для полных ДКА. Ведь для них поиск количества слов сводится к поиску в графе количества путей фиксированной длины из одной вершины к другой (из начального состояния в конечное).

4.2. Исследование конечного автомата

Обозначим за $L_{i, j}^{(n)}$ количество различных путей длины $inline$ из состояния $inline$ в состояние $inline$ и исследуем свойства получившихся величин.

Воспользуемся математической индукцией. $L_{i, j}^{(1)}$ — это просто число рёбер графа, ведущих из состояния $inline$ в состояние $inline$ , и вычисляется напрямую из описания конечного автомата.

Далее, допустим, что мы умеем вычислять все $L_{i, j}^{(n)}$ для какого-то $n \ge 1$ . Найдём $L_{i, j}^{(n+1)}$ .
Любой путь длины $inline$ неизбежно разбивается на начало пути длиной $inline$ и последним переходом длиной $inline$ . Причём "предпоследним" состоянием может быть совершенно любая вершина графа, обозначим её $inline$ .
Для каждой такой вершины число слов, проходящих сквозь неё на предпоследнем шаге, будет равно $L_{i, t}^{(n)} \cdot L_{t, j}^{(1)}$ . То есть произведение количества путей длины n на количество последующих путей длины 1 (количество соответствующих рёбер).

Взяв в расчёт все вершины $inline$ , приходим к формуле $L_{i, j}^{(n+1)} = \sum\limits_{t}(L_{i, t}^{(n)} \cdot L_{t, j}^{(1)})$ . Более того, проведя абсолютно те же самые рассуждения, можно получить формулу $L_{i, j}^{(n+r)} = \sum\limits_{t}(L_{i, t}^{(n)} \cdot L_{t, j}^{(r)})$ . Не то, что бы это было необходимо, скорее, помогает заметить закономерность.

Ничего не напоминает? Это один в один формулы для умножения матриц! Построим матрицу $inline$ в соответствии со значениями $L_{i, j}^{(1)}$ :

$L_m= \begin{pmatrix} L_{0,0}^{(1)} & L_{0,1}^{(1)} & \dots \\ \vdots & \ddots & \\ L_{m,0}^{(1)} & & L_{m,m}^{(1)} \end{pmatrix}$

Если использовать текущие обозначения, получим следующее общее выражение:

$L_m^n = \begin{pmatrix} L_{0,0}^{(1)} & L_{0,1}^{(1)} & \dots \\ \vdots & \ddots & \\ L_{m,0}^{(1)} & & L_{m,m}^{(1)} \end{pmatrix}^n = \begin{pmatrix} L_{0,0}^{(n)} & L_{0,1}^{(n)} & \dots \\ \vdots & \ddots & \\ L_{m,0}^{(n)} & & L_{m,m}^{(n)} \end{pmatrix}$

Симпатично вышло. Тем самым становится видно, что вычисление количества путей длины $inline$ сводится к возведению матрицы в степень $inline$ . Напомню, что данная формула применима к любому регулярному языку, если известен полный ДКА, который его описывает.

Матрицу $inline$ будем называть матрицей смежности. Для конкретного описанного ранее графа она выглядит следующим образом:

$L_{fuck} = \begin{pmatrix} 25 & 1 & 0 & 0 & 0 \\ 24 & 1 & 1 & 0 & 0 \\ 24 & 1 & 0 & 1 & 0 \\ 24 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 26 \end{pmatrix}$

Здесь видна явная закономерность в распределении единиц. Эта закономерность сохранится для более длинных "простых" слов:

$L_{hello} = \begin{pmatrix} 25 & 1 & 0 & 0 & 0 & 0 \\ 24 & 1 & 1 & 0 & 0 & 0 \\ 24 & 1 & 0 & 1 & 0 & 0 \\ 24 & 1 & 0 & 0 & 1 & 0 \\ 24 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 26 \end{pmatrix}$

Что же касается вычисления количества слов — оно равно количеству путей из единственного начального в единственное конечное состояние, т.е. $L_{0, m}^{(n)}$ . Если же возвращаться к изначальным обозначениям, то $C_m(n) = L_{0, m}^{(n)}$ для соответствующей матрицы $inline$ .
Т.к. вероятности мы выражали через $p_m(n) = \frac{C_m(n)}{26^n}$ , то новая формула для них будет выглядеть так:

$p_m(n) = \Big(\Big(\frac{L_m}{26}\Big)^n\Big)_{0, m}$

Понимаю, что очень много различных обозначений, но я просто не могу остановиться! Матрицу $\frac{L_m}{26}$ можно обозначить $inline$ . Она содержит не число путей из одного состояния в другое, а "вероятность перехода". Фактически она описывает однородную Цепь Маркова, соответствующую случайному блужданию по состояниям нашего графа с равномерной вероятностью выбора следующего ребра. Про цепи Маркова можно было вспомнить раньше, но да ладно.

4.3. Про возведения в степень

Теперь хотелось бы быстренько оценить трудоёмкость вычисления с помощью матриц. Для вычисления с помощью рекуррентного соотношения временная сложность была бы $inline$ .

Что же для матриц? Наивное итеративное возведение в степень дало бы $inline$ , а это хуже предыдущего результата. К счастью, возведение в степень за линейное время никто не осуществляет, ведь есть следующее правило:

$\left\{ \begin{array} &P_m^k = P_m^{k-1} \cdot P_m, & k = 2r + 1\\ P_m^k = (P_m^{k/2})^2, & k = 2r \end{array} \right.$

Подобный трюк позволяет понизить количество умножений до $O(\log(n))$ , тем самым давая общую трудоёмкость в $O(m^3 \log(n))$ — очень даже годится для практических вычислений.

Можно ещё кое-что сказать о возведении матриц в какие-нибудь степени. Согласно теореме Жордана, матрицу $inline$ можно представить в виде $P_m=C_mJ_mC_m^{-1}$ , где $inline$ — какая-то обратимая матрица, а $inline$ — Жорданова матрица, т.е. матрица, состоящая из Жордановых клеток. В частности, для случая простых слов типа fuck $inline$ — это диагональная матрица, содержащая на диагонали собственные числа матрицы $inline$ .

$J_m = \begin{pmatrix} \lambda_0 & \dots & 0\\ \vdots & \ddots & \\ 0 & & \lambda_m \end{pmatrix}$

Для доказательства этого факта достаточно показать, что у матрицы $inline$ нет повторяющихся собственных чисел. Можете попробовать сделать это самостоятельно (характеристический многочлен будет дан через несколько абзацев).

Жорданова форма облегчает возведение матриц в степени, в частности,

$P_m^n = (C_mJ_mC_m^{-1})^n = C_mJ_mC_m^{-1} \cdot C_mJ_mC_m^{-1} \dots C_mJ_mC_m^{-1} = C_m J_m^n C_m^{-1}$

Возведение в степень диагональной матрицы — задача тривиальная:

$J_m^n = \begin{pmatrix} \lambda_0^n & \dots & 0\\ \vdots & \ddots & \\ 0 & & \lambda_m^n \end{pmatrix}$

К чему я всё это? Взглянем на характеристический многочлен матрицы $inline$ :

$\chi(P_{fuck}) = \det(P_{fuck} - \lambda E) = Const*(1-\lambda)(\lambda^4-\lambda^3+\frac{1}{26^4})$

Должно выглядеть знакомо. И ведь действительно — $\mu_i$ из явной формулы являются корнями данного уравнения, вдобавок к этому есть дополнительный корень $\lambda_0=1$ .

Если же попробовать символьно перемножить матрицы $inline$ , $inline$ и $C_m^{-1}$ , то можно получить то же самое выражение, что и раньше:

$p_4(n)=(P_{fuck}^n)_{0, 4} = 1 + a\lambda_1^n + b\lambda_2^n + c\lambda_3^n + d\lambda_4^n$

Как найти характеристический многочлен данной матрицы. Читать необязательно.

Чтобы упросить дальнейшие формулы, уменьшив в них число делений, лучше рассмотрим характеристический многочлен матрицы $inline$ , имеющей $inline$ строк/столбцов и соответствующей "простому" слову длины $inline$ .

$\chi(L_m) = \det(L_m-\lambda E) = \begin{vmatrix} 25-\lambda & 1 & 0 & \dots & 0 & 0 & 0 \\ 24 & 1-\lambda & 1 & \dots & 0 & 0 & 0 \\ 24 & 1 & -\lambda & \dots & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 24 & 1 & 0 & \dots & -\lambda & 1 & 0 \\ 24 & 1 & 0 & \dots & 0 & -\lambda & 1 \\ 0 & 0 & 0 & \dots & 0 & 0 & 26-\lambda \end{vmatrix}$

Воспользуемся формулой разложения определителя по последнему столбцу, получим следующее:

$\chi(L_m) = (26-\lambda)\begin{vmatrix} 25-\lambda & 1 & 0 & \dots & 0 & 0 \\ 24 & 1-\lambda & 1 & \dots & 0 & 0\\ 24 & 1 & -\lambda & \dots & 0 & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 24 & 1 & 0 & \dots & -\lambda & 1 \\ 24 & 1 & 0 & \dots & 0 & -\lambda \end{vmatrix} - 1\begin{vmatrix} 25-\lambda & 1 & 0 & \dots & 0 & 0 \\ 24 & 1-\lambda & 1 & \dots & 0 & 0 \\ 24 & 1 & -\lambda & \dots & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 24 & 1 & 0 & \dots & -\lambda & 1 \\ 0 & 0 & 0 & \dots & 0 & 0 \end{vmatrix}$

У матрицы во втором слагаемом последняя строка полностью заполнена нулями, а, значит, и определитель этой матрицы равен нулю. То есть, про второе слагаемое можно забыть. Помним, что матрица в первом слагаемом теперь имеет $inline$ строк и столбцов.

Снова произведём разложение определителя, на этот раз по первой строке. Получим

$\chi(L_m) = (26-\lambda)\left[(25-\lambda)\begin{vmatrix} 1-\lambda & 1 & \dots & 0 & 0 \\ 1 & -\lambda & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & 0 & \dots & -\lambda & 1 \\ 1 & 0 & \dots & 0 & -\lambda \end{vmatrix} - 1\begin{vmatrix} 24 & 1 & \dots & 0 & 0 \\ 24 & -\lambda & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 24 & 0 & \dots & -\lambda & 1 \\ 24 & 0 & \dots & 0 & -\lambda \end{vmatrix} \right]$

Теперь матрицы в обоих слагаемых имеют $inline$ строк и столбцов. Важно за этим следить.
Заметим, что во второй матрице можно вынести 24 из первого столбца. Первую же матрицу снова разложим по первой строке:

$\chi(L_m) = (26-\lambda)\left[(25-\lambda)\left( (1-\lambda)\begin{vmatrix} -\lambda & 1 & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \dots & -\lambda & 1 \\ 0 & 0 & \dots & 0 & -\lambda \end{vmatrix} - 1\begin{vmatrix} 1 & 1 & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & 0 & \dots & -\lambda & 1 \\ 1 & 0 & \dots & 0 & -\lambda \end{vmatrix} \right) - 24\begin{vmatrix} 1 & 1 & \dots & 0 & 0 \\ 1 & -\lambda & \dots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 1 & 0 & \dots & -\lambda & 1 \\ 1 & 0 & \dots & 0 & -\lambda \end{vmatrix} \right]$

Мы получили выражение, в котором содержатся только матрицы очень простой структуры. Обозначим их $inline$ и $inline$ и перепишем выражение в новых терминах. Нижний индекс для $inline$ и $inline$ — число строк в матрицах:

$\chi(L_m) = (26-\lambda)\left[(25-\lambda)\left( (1-\lambda)\det(A_{m-2}) - \det(B_{m-2}) \right) - 24\det(B_{m-1}) \right]$

Здесь я не буду расписывать всё настолько подробно. Матрица $inline$ — верхне-треугольная, её определитель равен $\det(A_k) = (-\lambda)^k$ .

С матрицей $inline$ немного сложнее. Думаю, к этому моменту разложение определителя не должно вызывать проблем, поэтому сделаем его в уме (по первой строке):

$\det(B_k) = 1\cdot\det(A_{k-1}) - 1\cdot\det(B_{k-1}) = (-\lambda)^{k-1} - det(B_{k-1})$

Воспользовавшись математической индукцией (а потом формулой суммы геометрической прогрессии), несложно будет доказать, что

$\det(B_k) = (-1)^{k+1}(\lambda^{k-1} + \lambda^{k-2} + \dots + \lambda + 1) = (-1)^{k+1}\frac{\lambda^k - 1}{\lambda - 1}$

Подставив результаты в исходную формулу и упростив выражение несколько раз, получим

$\chi(L_m) = (26-\lambda)\left[(25-\lambda)\left( (1-\lambda)(-\lambda)^{m-2} - (-1)^{m-1}\frac{\lambda^{m-2} - 1}{\lambda - 1} \right) - 24(-1)^m\frac{\lambda^{m-1} - 1}{\lambda - 1} \right] \\ = (26-\lambda)\left[ (25-\lambda)(1-\lambda)(-\lambda)^{m-2} + (-1)^m(25-\lambda)\frac{\lambda^{m-2} - 1}{\lambda - 1} - 24(-1)^m(\lambda^{m-2} + \frac{\lambda^{m-2} - 1}{\lambda - 1}) \right] \\ = (26-\lambda)\left[ (25-\lambda)(1-\lambda)(-\lambda)^{m-2} - 24(-\lambda)^{m-2} + (-1)^m(25-\lambda - 24)\frac{\lambda^{m-2} - 1}{\lambda - 1}) \right] \\ = (-1)^m (26-\lambda)\left[ (25-\lambda)(1-\lambda)\lambda^{m-2} - 24\lambda^{m-2} - (\lambda^{m-2} - 1) \right] \\ = (-1)^m (26-\lambda)\left[ 25\lambda^{m-2} - 26\lambda^{m-1} + \lambda^m - 24\lambda^{m-2} - \lambda^{m-2} + 1 \right] \\ = (-1)^m (26-\lambda)\left[ \lambda^m - 26\lambda^{m-1} + 1 \right]$

То есть

$\chi(L_m) = (-1)^m (26-\lambda)\left[ \lambda^m - 26\lambda^{m-1} + 1 \right]$

Дальше всё понятно, нужно просто сделать замену переменной в получившейся формуле.

5. Общий случай

На протяжении статьи я употреблял фразу "простое слово", не давая ей точного определения. Постараюсь это исправить. Рассмотрим пример, пусть есть алфавит из трёх символов — {a, b, c}. Посчитаем все слова длиной 3, которые содержат подслово ab: aab, aba, abb, abc, bab и cab. Всего 6 слов из 27-ми.

Если же искать слово aa, то вариантов останется всего пять: aaa, aab, aac, baa и caa. То есть вероятность заметно понизилась.

На самом деле для слова aa предпосылки, на которых мы строили изначальную рекуррентную формулу, ломаются, и использовать эту формулу попросту нельзя.
А именно, ломается подсчёт количества слов, которые "заканчиваются на aa и содержат его более, чем один раз". В этом месте при выводе формулы мы неявно допустили, что у искомого слова нет суффикса, совпадающего с её префиксом. Для fuck свойство выполнено, а для aa — нет.

На примере строк похожей длины, предлагаю рассмотреть слово abab, у него как раз есть префикс ab, совпадающий с суффиксом:

Матрица смежности для него, соответственно, тоже будет отличной. Имеющиеся ранее закономерности нарушены, да и характеристический многочлен другой (считать не буду, просто поверьте):

$L_{fuck} = \begin{pmatrix} 25 & 1 & 0 & 0 & 0 \\ 24 & 1 & 1 & 0 & 0 \\ 24 & 1 & 0 & 1 & 0 \\ 24 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 26 \end{pmatrix} \ L_{abab} = \begin{pmatrix} 25 & 1 & 0 & 0 & 0 \\ 24 & 1 & 1 & 0 & 0 \\ 25 & 0 & 0 & 1 & 0 \\ 24 & 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 26 \end{pmatrix}$

Казалось бы, совсем чуть-чуть отличается одна строка, а какой эффект. Получается, что эти матрицы отличаются достаточно сильно, чтобы ответы в итоге получались разные.

С другой стороны, есть слова, для которых рассуждения о рекуррентном соотношении всё ещё справедливы, но конечный автомат для которых тоже сильно отличается от исходного. Например, слово aaab:

$L_{aaab} = \begin{pmatrix} 25 & 1 & 0 & 0 & 0 \\ 25 & 0 & 1 & 0 & 0 \\ 25 & 0 & 0 & 1 & 0 \\ 24 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 26 \end{pmatrix}$

Эта матрица отличается от обеих матриц, приведённых до неё, но всё равно приводит к ответу, совпадающему с таковым для слова fuck! Более того, совпадает не только ответ, но и характеристический многочлен. Матрицы $L_{fuck}$ и $L_{aaab}$ имеют одну и ту же Жорданову форму, и вот это уже совсем неочевидно по их внешнему виду.

Далее, помимо длины общего префикса/суффикса, на конечный ответ могут влиять и другие факторы. Например, есть ли у префикса/суффикса свой собственный, более короткий префикс/суффикс, и т.д.

Для получения истиной, общей процедуры получения ответа, проще всего построить для слова соответствующий конечный автомат, а по автомату — матрицу, и возводить её в нужную степень. Обобщение рекуррентного соотношения слишком сложно сделать.
Тут я уже не буду никого утомлять точным способом построения ДКА, что-то очень похожее есть, например, в алгоритме Ахо — Корасик. Тот же алгоритм поможет определить вероятность того, что в вашей строке есть нехорошее слово из заранее подготовленного словаря.

Заключение

Кажется, я не ответил на вопрос "Что, если взять другой алфавит?". Замените 26 на другое число, вот и всё.

Что в итоге. Интересную задачу посмотрели, математику младших курсов вспомнили, выводов особо не сделали. Моей целью было немного развлечь читателя и, может быть, показать что-то новое — надеюсь, было интересно. Думаю, наибольшую пользу из статьи смогут извлечь как раз-таки студенты. Код не привожу, да и стали бы вы его читать?

Спасибо за внимание!

Комментарии (79)

wataru
26.11.2023 20:20
#26201168
+4
Я в своей статье рассматривал похожую задачу. Вместо вероятности набрать за k символов, я считал матожидание количества символов до первого совпадения. Там получилась явная формула через префикс функцию. Кажется, можно применить это же свойство конечного автомата для строки и получить более простую формулу.

Rsa97
26.11.2023 20:20
#26201174
-5
Если умеешь считать до десяти, остановись на пяти.
На шаге 2 получена не приблизительная, а точная формула. Дальнейшие расчёты никакого смысла не имеют.
1. ibessonov Автор
  26.11.2023 20:20
  #26201190
  +6
  На шаге 2 получена приблизительная формула, и я даже вкратце объяснил почему. Точное значение отличается от приблизительного, пусть и не очень сильно. Пожалуйста, прочитайте немного дальше прежде чем судить, спасибо!
  1. sci_nov
    26.11.2023 20:20
    #26201304
    +1
    простой способ проверить точность формул - взять слово из трех букв, а длину последовательности (ID) задавать, например, {4, 5, 6}. В этом случае метод Монте-Карло должен сойтись быстрее. Заголовок статьи у Вас четкий, постановка задачи понятна и, кажется, ответ (точная формула) должен быть простым.
  1. Rsa97
    26.11.2023 20:20
    #26201602
    +3
    Да, прошу прощения, абзац про повторения я как-то пропустил и сам не сообразил.
1. sci_nov
  26.11.2023 20:20
  #26201272
  Тер.вер. он такой)
1. wataru
  26.11.2023 20:20
  #26201292
  +3
  Нет, там приблизительная формула, потому что строки, в котороых "fuck" встречается несколько раз подсчитаны больше одного раза в ответе. Для вот такой строки, два вхождения которой не могут пересекаться, можно еще применить формулу включения-исключения, но там будет не очень просто. Дам будет сумма по количеству вхождений, а внутри какие-то сочетания и все это умножить на 26^(n-4i).
  
  Для какой-нибудь строки "aba" уже замучаешься формулу применять, потому что там может быть просто огромное количество случаев. Ибо строка хотя бы с тремя вхождениями "aba" может иметь их в 9 различных символах в трех группах по три, в 8 символах в групах по 5 и по 3, и в 7 символах в одной группе. Можно, наверно, составить какие-то рекуррентные соотношения, но они не будут сильно проще той же матрицы переходов в ДКА.

konst90
26.11.2023 20:20
#26201886
+3
Артур Кларк. Девять миллиардов имён Бога.
1. MiyuHogosha
  26.11.2023 20:20
  #26202370
  Там скорее задача о пермутациях. По описанию на строки еще накладывались ограничения.

sci_nov
26.11.2023 20:20
#26202196
Кстати, код как раз то и нужен, чтобы наверняка понять как Вы определяете истинность условия задачи: некоторое слово входит в строку.

sci_nov
26.11.2023 20:20
#26202420
Вы кажется нашли вероятность того, что fuck встретится ровно один раз - эта задача да, сложнее.
1. ibessonov Автор
  26.11.2023 20:20
  #26202426
  В статье найдена вероятность того, что fuck встретится хотя-бы один раз. На самом деле мне казалось, что и описание, и содержание явно об этом говорят, может быть мне стоило более аккуратно выбирать формулировки.
  Касательно Вашего предыдущего вопроса про код - на привычной мне Java это было бы str.contains("fuck").
  1. sci_nov
    26.11.2023 20:20
    #26202432
    Хех, тогда прав Rsa97.
    
    ibessonov Автор
    26.11.2023 20:20
    #26202448
    +2
    Как раз таки нет, Rsa97 не прав. В приблизительном решении слово "fuckfuckfuckfuckfuck" (5 раз, ровно 20 букв) будет учтено 5 раз вместо одного, именно по этой причине приведённая оценка завышена. Дальнейшие рассуждения исключают подсчёт одних и тех же строк несколько раз.
    
    sci_nov
    26.11.2023 20:20
    #26202598
    Да, точно... Вот fuck так fuck)

domix32
26.11.2023 20:20
#26202934
+3
Так а вероятность-то финальная какая? Приблизительно посчитали, а точно-то где? Искали вероятность, а получили матрицу.
1. ibessonov Автор
  26.11.2023 20:20
  #26202978
  +2
  Реальная вероятность дана в пункте 3.1, равна 0.00003720064..., вычислена по рекуррентной формуле. Дальше идёт общий случай
  1. domix32
    26.11.2023 20:20
    #26202988
    За что ж вы их всех в формулу...

vashwind
26.11.2023 20:20
#26203158
+1
Эмм, тер вер 1 курс.

Вероятность слова fuck с первой позиции:

1/26 * 1/26 * 1/26 * 1/26 и сложить вероятности со всех 17 возможных начальных позиций.

1/26/26/26/26*17 = 0.000037201...

Ну как бы и всё...

К чему всё остальное в статье городить?
1. ibessonov Автор
  26.11.2023 20:20
  #26203212
  +1
  Остальное городить к тому, что вы ошиблись. Это сказано и в статье, и в комментариях. Данную ошибку уже совершили несколько людей. Ваш вариант считает некоторые слова по несколько раз, в частности слова, которые содержат fuck 2 и более раз. Так что могу лишь попросить быть внимательнее
  1. vashwind
    26.11.2023 20:20
    #26203238
    Задача звучит так - Какова вероятность найти слово fuck в случайной последовательности из 20 букв?
    
    В моём ответе показана вероятность, что в последовательности букв встречается это слово хотя бы один раз.
    
    В чем противоречие то?
    
    ibessonov Автор
    26.11.2023 20:20
    #26203240
    +2
    Вы посчитали часть слов несколько раз, т.е. ваше вычисление - неточное
    
    vashwind
    26.11.2023 20:20
    #26203246
    -2
    Я не считал никакие слова, я посчитал вероятность появление хотя бы одного этого слова в этой последовательности.
    
    Вы либо условие задачи измените, либо теорию вероятностей почитайте, основы за первый курс.
    
    ibessonov Автор
    26.11.2023 20:20
    #26203260
    Мне потребуется немного времени, чтобы дать вам развёрнутый ответ. Добавлю его в эту ветку комментариев.
    Пока лишь скажу - перед тем как обвинять кого-то в незнании основ, пожалуйста, убедитесь на 100%, что сами не ошиблись.
    
    ibessonov Автор
    26.11.2023 20:20
    #26203302
    +3
    Итак.
    
    В чем противоречие то?
    
    Вообще говоря, для того, чтобы вероятности складывать, события должны быть независимы, а свойство независимости у нас не соблюдено. Рассмотрим простой пример. Пусть в алфавите 2 буквы - "a" и "b". Мы ищем включение слова "a" в последовательностях из 2-х букв, для простоты. Я довожу пример до абсолютного минимума, чтобы не было никаких вопросов (надеюсь). Итак, слово "a" встречается в начале у двух слов - "aa" и "ab", т.е. с веорятностью 0,5. Слово "a" встречается в конце у двух слов - "aa" и "ba", т.е. с вероятностью 0,5.
    Казалось бы, если поступить как Вы и сложить ответы, то должно получиться 2*0,5 = 1, что было бы весьма абсурдным заявлением. Перечислив все слова явно, мы получим "aa", "ab" и "ba", т.е. 0,75.
    1 больше, чем 0,75. Как я и говорил в статье, эта вероятность является завышенной. Надеюсь теперь стало понятно.
    
    ibessonov Автор
    26.11.2023 20:20
    #26203404
    +3
    Ладно уж, сказал A - говорю B. Правильный вариант складывания вероятностей: P(A | B) = P(A) + P(B) - P(AB), нужно не забыть отнять вероятность того, что A и B пересекаются. В моём примере это только строка "aa". Если подставить всё в формулу, то получим P = 0,5 + 0,5 - 0,25 = 0,75, то есть правильный ответ. Вот вам основы за первый курс
    
    AgentFire
    26.11.2023 20:20
    #26203956
    Тогда почему у него ответ такой же получится?
    
    ibessonov Автор
    26.11.2023 20:20
    #26203976
    +2
    У него ответ - 0.0000372010, у меня ответ - 0.0000372006. Числа близкие, но разные, это важно
  1. premierhr
    26.11.2023 20:20
    #26209190
    Если мы рассмотрим бесконечный поток случайно генерируемых символов, период повторения нецензурного слова по стремящейся к бесконечности последовательности будет 26^4 символов. перемещая окно в 20 символов по этому потоку только в 17 из 26^4 случаев результат будет положительный. я могу ошибаться, но это и называется вероятностью. Без повторов нецензурного слова.
    
    ibessonov Автор
    26.11.2023 20:20
    #26209272
    Определение вероятности выглядит совершенно иначе, в нём не участвует бесконечный поток символов.
    Так или иначе, вы повторили распространённую ошибку, связанную с числом 17. В статье объяснено, почему этот ответ неверный. В комментариях к статье есть более подробные объяснения.
    
    premierhr
    26.11.2023 20:20
    #26211242
    Безусловно есть вероятность вхождения плохого слова в строку из 20 символов больше 1 раза. При этом нет нужды объяснять, что в следующий раз эта вероятность будет сильно меньше искомой. Вероятность при этом можно определить как матожидание периода выпадения благоприятного исхода = 1/26^4 и оно не меняется!. Размещаться в последовательности из 20 символов оно может 17 способами. "Вероятностью P(A) события A называется отношение числа элементарных событий m, благоприятствующих событию A, к числу всех элементарных событий n." Так что нет, у меня проблем с определением вероятности нет. Вы нарочно усложнили себе решение, там где этого не требуется.
    
    wataru
    26.11.2023 20:20
    #26211260
    +1
    Рассмотрите тест попроще. 2 буквы в алфавите, слово "ab", текст длиной 4. Ваша формула дает ответ 3/2^2 = 3/4. Когда как ответ 11/16 ("abaa", "abab", "abba", "abbb", "aaba", "aabb", "baba", "babb", "aaab", "baab", "bbab"). Или проще - строки, где "ab" не встречается, являются упорядоченными по невозрастанию букв. Их всего 5: "bbbb", "bbba", "bbaa", "baaa", "aaaa".
    
    Проблема в том, что слово "abab" в вашей формуле подсчитается 2 раза, когда окно в начале текста и когда оно в конце текста.
    
    Это в точности та же проблема, что и с приблизительной формулой автора из статьи.
    
    ibessonov Автор
    26.11.2023 20:20
    #26211280
    Вероятность при этом можно определить как матожидание периода выпадения благоприятного исхода
    
    В конце вы предложили нормальное определение, через отношение. С ним я согласен. Но вот с 17/26^4 я согласиться не могу, это неправильный ответ, и в статье сказано почему. Количество событий в числителе просто не такое, проверьте те же рассуждения хотя бы для строк длиной 8, для них можно получить точный ответ на листке бумаги, это 5*26^4-1. Единицу отнимать - обязательно, потому что она соответствует строке с двумя вхождениями плохого слова.
    Я не усложняю решение, это вы пытаетесь его упростить, при этом допускаете ошибку в рассуждениях. Пожалуйста, ознакомьтесь с содержанием статьи ещё раз, спасибо!
    
    premierhr
    26.11.2023 20:20
    #26211476
    +1
    спасибо!

sci_nov
26.11.2023 20:20
#26203280
Право дело, Вы меня подстегнули. Я нашел некоторое решение, но другим путём: вероятность $3.7200427144... \cdot {10}^{-5}$ (привлек BigFloat, чтобы наверняка)... Ниже, чем по приближенной формуле, но и чуть ниже вашего точного решения. Возможно потому что я искал для любого фиксированного слова из 4-х символов.

Логика была следующая: искомое слово состоит из 4-х символов, поэтому его можно искать в некоторой строке 4-мя потоками, которые можно пронумеровать 0, 1, 2 и 3, что соответствует сдвигу на один символ (4 фазы). Причем искать следует с шагом 4 символа (для этого и было сделано деление на потоки). Легко найти вероятность события: ни одно слово в -м потоке не найдено
$p(i) = {\left(1 - {(1/26)}^{4}\right )} ^ {\lfloor {{n-i} \over {4}} \rfloor}$
Теперь находим вероятность события: ни одно слово не найдено во всех 4-х потоках - найденные на предыдущем шаге вероятности перемножаются (потоки в плане поиска фиксированного слова независимы). Далее находим вероятность противоположного события: хотя бы одно слово встретилось, то есть из единицы вычитаем найденное произведение вероятностей
1. wataru
  26.11.2023 20:20
  #26203494
  +1
  У вас ошибка в том, что нельзя перемножать вероятности для разных потоков. Ведь они не независимы. Когда в первом потоке слова нет среди первых двух повторений, строка "xxxf uckx..." не может быть во втором потоке, но вы ее такую там подсчитаете. В примере с fuck и 26 символами все сложно, но давайте расмотрим слово "ab" над алфовитом из только a и b. И n=3. У вас тут 2 потока. Ваша формула даст 1-(1-0.5^2)^2= 7/16. Что точно неверно, потому что слов из трех букв всего 8 и ответ к задаче должен быть представим в виде рациональной дроби со знаменателем 8.
  1. sci_nov
    26.11.2023 20:20
    #26204372
    Согласен. Тогда видимо у меня нижняя оценка, а приближенная формула в статье - верхняя оценка.
  1. sci_nov
    26.11.2023 20:20
    #26204410
    Если искать "ab" (или "ba"), то будет 4/8, а если искать "aa" (или "bb"), то будет 3/8. В среднем будет 1/2*(4/8 + 3/8) = 7/16 )))

nameisBegemot
26.11.2023 20:20
#26203372
+1
Целая наука по поиску слова фуск

phenik
26.11.2023 20:20
#26203726
+1
Какова вероятность найти слово fuck в случайной последовательности из 20 букв?

Вот здесь оценивается вероятность более грандиозного замысла - какова вероятность того, что обезьяна напечатает текст "Гамлета" случайно стуча по клавишам пишущей машинке с первой попытки. Получилось 1.0×10^−360,783

Оценки имеющие эволюционные и другие следствия. Еще оценки вероятностей событий, иногда точнее их невероятностей)

iShrimp
26.11.2023 20:20
#26203844
+1
Интересная задача на комбинаторику. Если можно, хотел бы поделиться ещё одной задачей, которую вообще непонятно как решать.

В комиссионный магазин в случайном порядке пришли 2*N человек, из которых N хотят купить некий предмет (пусть будет пальто), а другие N человек хотят продать этот же предмет. В самом начале магазин пуст. Какова вероятность, что продавец сможет обслужить всех клиентов?
1. ibessonov Автор
  26.11.2023 20:20
  #26203876
  Если можно
  
  А что нельзя то, интересная задача! Сходу как решать тоже не знаю, но на досуге подумаю, спасибо!
1. wataru
  26.11.2023 20:20
  #26204280
  +3
  Этож правильные скобочные последовательности. Для продающего запишем "(" в строку, для покупающего ")". Все получится, если последовательность скобок - правильная. Всего их C(2n, n)/(n+1) - они же числа каталана.
  
  Каждую последовательность можно набрать n!*n! способами (перемешать левые и правые скобки отдельно, Всего вариантов прийти - (2n)!
  
  Делим количество хороших вариантов на общее количество, факториалы сокращаются и остается 1/(n+1). Это и есть ответ.
  
  Проверка, n=1: есть 2 варината, в одном все хорошо. 1/2 - все совпадает. n=2: с вероятностью 1/2 первый будет покупать и все плохо. В оставшемся случае все плохо, если второй продавец окажется последним. Итого все хорошо в 1/2*(1-1/3) = 1/3 случаев. Опять совпало.

ultrinfaern
26.11.2023 20:20
#26203982
-1
Решаем задачу классически:

Дано строка размера n с подстрокой размера m, вариантов каждого элемента k.

Вычисляем количество успешных вариантов - это сама подстрока плюс все возможные варианты каждого элемента и их n-m - итого k^(n-m)

Всего комбинаций - k^n

Вероятность - успешные варианты / всего вариантов - k^(n-m)/k^n
1. ibessonov Автор
  26.11.2023 20:20
  #26203996
  +1
  Предлагаю вам подставить в ваши формулы конкретные небольшие значения n/m/k и проверить, совпадают ли они с истиным решением (которое легко получить перебором на листочке)
  1. ultrinfaern
    26.11.2023 20:20
    #26204034
    -1
    Давайте подставим - предположим у нас один символ и мы его и ожидаем. Понятно, что его вероятность 1/k. По формуле - к^0/k^1 = 1/k
    
    Домашнее задание, рассмотреть строку из двух симвлов где один ожидаемый, и убедиться, что верояность соответствует формуле.
    
    wataru
    26.11.2023 20:20
    #26204288
    Это у вас n=m=1 - самый тривиальный случай. А уже хотя бы n=2, m=1 у вас все сломается.
    
    ultrinfaern
    26.11.2023 20:20
    #26204334
    Моя ошибка - учел вероятность нахождения последовательности в определленой позиции. Позиций всего (n-m+1)
    
    Итог - ((n-m+1)*k^(n-m))/k^n
    
    wataru
    26.11.2023 20:20
    #26204376
    И? Ну подставьте же m=1. Ответ должен быть 1-(k-1)^n/k^n. У вас получается что угодно, но не это.
    
    ultrinfaern
    26.11.2023 20:20
    #26204452
    import java.security.SecureRandom;
    
    public class Main {
    private static int CCC = 1000_000_000;
    private static int K = 10;
    private static int N = 5;
    
    private static int[] ETALON = {1, 2, 1}; private static boolean check(int[] x) { var cnt = x.length - ETALON.length + 1; for (int d = 0; d < cnt; d++) { var eq = true; for (int i = 0; i < ETALON.length; i++) { if (x[d + i] != ETALON[i]) { eq = false; break; } } if (eq) { return true; } } return false; } public static void main(String[] args) { try { var r = SecureRandom.getInstanceStrong(); int cnt = 0; for (int i = 0; i < CCC; i++) { var probe = new int[N]; for (int j = 0; j < N; j++) { probe[j] = r.nextInt(K) + 1; } //check if (check(probe)) { cnt = cnt + 1; } } System.out.println("cnt = " + cnt); System.out.println("% = " + (((double)(cnt)) / CCC)); } catch (Exception e) { System.out.println("Ops!: " + e.getMessage()); } }
    
    }
    
    Прогон програмы - результат cnt = 2990046, % = 0.002990046
    
    По формуле - ((5-3+1)*10^2)/10^5 = 300/10000 = 0.003
    
    Формула правильная.
    
    ibessonov Автор
    26.11.2023 20:20
    #26204480
    Не могли бы вы в коде сгенерировать все возможные строки по 1 разу, чтобы получить точное значение вместо приблизительного? Чтобы сравнивать наверняка, без погрешностей?
    Кажется, текущие значения достаточно малы, чтобы программа могла быстро со всем справиться. Спасибо!
    
    ultrinfaern
    26.11.2023 20:20
    #26204536
    Вы о чем?! Какая вероятность что взятые от балды N, M, К, ETALON совпадут с фомулой?
    
    Давайте по другому - у вас есть программа, у вас есть формула - контрпример в студию!
    
    ЗЫ Только имейтке ввиду что количество интераций CCC дожно быть гораздо больше чем K^N - тогда у вас будет нормальный результат. В примере - 10000 / 1000000000 = 0,00001 - вполне достаточная цифра по сравнению с 0.003.
    
    ЗЫЗЫ И вы НИКОГДА не пролучите точное значение из программы. Для точного значения требуется сделать БЕСКОНЕЧНОЕ число попыток.
    
    ibessonov Автор
    26.11.2023 20:20
    #26204674
    И вы НИКОГДА не пролучите точное значение из программы. Для точного значения требуется сделать БЕСКОНЕЧНОЕ число попыток
    
    Вы серьёзно? Это даже не смешно. То есть я не могу в программе сгенерировать ВСЕ строки длиной 10 из алфавита, в котором 5 символов? Так то могу.
    Вы же знаете, что такое дискретное распределение? Кажется самое время подтянуть матчасть
    
    ultrinfaern
    26.11.2023 20:20
    #26204722
    -1
    Я вас разочарую, да НИКОГДА. Потому что программа показывет частоту события а формула дает вероятность события. В чем разница - гугл или книжка по теории вероятности.
    
    ibessonov Автор
    26.11.2023 20:20
    #26204762
    +1
    Вы же сами знаете, что такое вероятность? Беседа зашла в тупик.
    Отвечаю последний раз. У нас есть вероятностное пространство, состоящее из всех строк длины 10. Это пространство - конечно.
    Возможные исходы - это подмножества данного вероятностного пространства. Вероятности исходов равны числу элементов в них, делëному на число элементов в вероятностном пространстве.
    Исход, который нас интересует - конкретное подмножество строк. Мы можем программно вычислить и само подмножество, и его размер.
    Всё, что я написал - это основы основ. Я не понимаю, в чём вы хотите меня убедить, не зная базовых определений. Пожалуйста, не будьте настолько самоуверенным чтобы даже не допускать собственной неправоты. Подумайте ещё раз перед ответом. Повторите теорию. И тогда поймëте, где вы ошиблись.
    EDIT: забыл сказать. Распределение, естественно, равномерное
    
    ultrinfaern
    26.11.2023 20:20
    #26204808
    Я вел речь про свою программу, исходный код которой выше. И все мои высказывания касаются указанной программы. Судя по всему мы говорим про разные вещи.
    
    ultrinfaern
    26.11.2023 20:20
    #26204672
    Очередной тест:
    
    K = 5
    N = 10
    ETALON = {2, 1, 4, 3}
    M = 4
    
    cnt = 11187608, % = 0.011187608
    
    ((N - M + 1) * K ^ (N - M)) / K ^ N
    
    ((10 - 4 + 1) * 5 ^ (10 - 4)) / 5 ^ 10
    7 * 5 ^ 6 / 5 ^ 10
    7 * 15625 / 9 765 625 = 0.0112
    
    Опять сходится!
    
    ibessonov Автор
    26.11.2023 20:20
    #26204840
    +1
    У вас вышло 109375 / 9 765 625.
    Точный ответ, если я не ошибся при вычислении на телефоне (код напишу уже утром) - 109225 / 9 765 625.
    То есть чуть-чуть меньше. И это легко проверяется полным перебором в программе.
    Точность вероятностной проверки не позволит вам доказать правильность вашей формулы, потому что погрешность вычисления получается больше, чем ошибка формулы.
    
    ibessonov Автор
    26.11.2023 20:20
    #26205588
    private static final String ETALON = "2143"; private static final int K = 5, N = 10; public static void main(String[] args) { // K ^ N long kn = 1; for (int i = 0; i < N; i++) { kn *= K; } long count = 0; for (long i = 0; i < kn; i++) { // Format string with 0 padding. String str = Long.toString(i + kn, K).substring(1); if (str.contains(ETALON)) { count++; } } System.out.println(count + " / " + kn); }
    
    Ответ тот же, что я дал вчера: 109225 / 9765625

Batalmv
26.11.2023 20:20
#26204082
Я почитал статью и мне кажется есть решение проще. Без матриц, на примере слова FUCK

Сначала о том, что считаем в несколько иной формулировке (тоже самое, но так более соответствует алгоритму). Какова вероятность того, что "программа" найдет слово FUCK в последовательности символов, которые ей будут выдавать кортежами по 4 символа?

По сути это тоже самое, просто мы берем сразу по 4 символа (это позволяет взглянуть на задачу по другому, без внесения сложностей, которые и так есть)

Итак, для итерации 0 все очевидно: вероятность найти слово FUCK == 1 - 1\26^4. Понятно почему. Дальше обычная ресурсия.

Сначала важный момент. Так как события "не найдено слово FUCK на N-1 итерации" и "не найдено слово FUCK на N итерации" связаны, то для итогового результата надо вероятности итераций перемножать, начиная с "зерна"

Теперь распишем итерации

В рамках одной итерации все кортежи выпадают независимо, поэтому их вероятности "в пределах одной итерации, как отдельного события можно складывать". Это тоже важно. Итак, есть следущие варианты:

1/26^4 - FUCK
25/26 * 1/26^3 - ?FUC
1/26^4 - KFUC
25/26 * 25/26 * 1/26^2 - ??FU
25/26 * 1/26^3 - K?FU
1/26^4 - CKFU
25/26 * 25/26 * 25/26 * 1/26 - ???F
25/26 * 25/26 * 1/26^2 - K??F
25/26 * 1/26^3 - CK?F
1/26^4 - UCKF
25/26 * 25/26 * 25/26 * 25/26 - ????
25/26 * 25/26 * 25/26 * 1/26 - K???
25/26 * 25/26 * 1/26^2 - CK??
25/26 * 1/26^3 - UCK?

Слева вероятность, справа кортеж. Знак ? - просто любой символ, который не "делает" слово FUCK. По сути все просто, есть префикс, есть суффикс (ну или начало и окончание). Вероятности тоже понятно как подсчитаны

По гипотезе (кажется это когда-то мат. индукцией) на итерации N-1 у нас слово FUCK не найдено и "програма" работает дальше (мы помним, что в расчетах вероятности каждой итерации надо перемножить как зависимые события).

Прилете следующий кортеж и там те же варианты, поэтому таблицу дублировать не буду. Итак, какая вероятность того, что "програма" найдет слово FUCK

Это банальное сочетание кортежа из N-1 итерации и кортежа из N-итерации, или более предметно варианты

1/26^4 + // В N кортеже прилетел "FUCK" и по сути все равно, кто было в N-1
(25/26 * 1/26^3 + 1/26^4) * (1/26^4 + 25/26 * 1/26^3 + 25/26 * 25/26 * 1/26^2 + 25/26 * 25/26 * 25/26 * 1/26) + // "FUC" из N-1 и "K" из N
(25/26 * 25/26 * 1/26^2 + 25/26 * 1/26^3 + 1/26^4) + (1/26^4 + 25/26 * 1/26^3 + 25/26 * 25/26 * 1/26^2) + // "FU" из N-1 и "CK" из N
(25/26 * 25/26 * 25/26 * 1/26 + 25/26 * 25/26 * 1/26^2 + 25/26 * 1/26^3 + 1/26^4) * (1/26^4 + 25/26 * 1/26^3) // "F" из N-1 и "UCK" из N

Полученное складываем и отнимаем от 1. Я не буду делать, просто лениво перебивать это куда-то типа Excel или калькулятора, но и так понятно, что вышла константа (обозначим за А)

Дальше просто считаем (1 - 1\26^4)*(1 - А)^<сколько было четверок>

--------------

Понятно, если N не кратно 4м - ну блин, концевой кортеж тоже надо подсчитать, но понятно как и вот

Я предполагаю, что если вероятность поймать FUCK на итерации аккуратно выписать, то там можно будет кой чего посокращать и вообще вывести формулу для любого слова. Отдельно неприятным моментов может быть усложнение формулы для другого слова, где будет повторение букв или его частей

------------

Если где-то налажал - напишите, но если я прав - то вроды вышло просто и в рамках школьной математики старшей школы
1. ibessonov Автор
  26.11.2023 20:20
  #26204178
  Насколько я вижу, вы тоже построили конечный автомат, в котором символы для перехода - это четвёрки. Далее вы попробовали использовать простую формулу, возводящую число в степень, для оценки вероятности, но дело в том, что вероятность на каждом шаге - условная, именно поэтому необходимо возводить в степень матрицу, а не одно число. Тут же буквально цепь Маркова. Это если совсем вкратце.
  На самом деле я затрудняюсь кратко объяснить, почему возведение числа в степень - ошибочно, а долгое объяснение - и писать будет долго. Могу предложить поиграться с более короткими строками.
  Дело в том, что при любом правильном подходе формулы должны получиться одни и те же, ну или как минимум тождественные, это было показано в статье. Если это не так - нужно искать ошибку в рассуждениях
  1. Batalmv
    26.11.2023 20:20
    #26204358
    алее вы попробовали использовать простую формулу, возводящую число в степень, для оценки вероятности, но дело в том, что вероятность на каждом шаге - условная, именно поэтому необходимо возводить в степень матрицу, а не одно число. Тут же буквально цепь Маркова. Это если совсем вкратце.
    
    Так откуда матрица?
    
    Никакого автомата нет, просто обработка идет сразу 4 символа за раз. И все.
    
    Формулу я не пробовал. Смотрите, я просто разбил пространство всех возможных событий на "элементарные", сумма вероятностей которых == 1. Все. Формула вышла из рассуждений, а не просто потому что я ее использовал :)
    
    Я ж расписал, как я к формуле пришел. На каждом шагу после обработки 4ки алгоритм либо находит FUCK, либо нет. Но прикол в том, что вероятность этого зависит от того что придет в ЭТОЙ четверке и предыдущей. И все. Ну это очевидно в виду длины слова FUCK. А чтобі учесть все варианты, я просто скрупулезно подсчитал вероятности событий, когда преддыдущая четверка и текущая склеенные вместе, образуют искомое слово. И все
    
    И получаеться в итоге обычная функция (1 - А)^N. Которая элементарно рассчитывается.
    
    ---------------
    
    Я просто тоже "подолбился" обрабатывая символы по одному, но потому понял, что получается избыточная сложность, с которой надо как-то бороться. А кортежи длиной в искомое слово эту сложность сводят к конечному и простому числу вариантов. Условно
    
    ???????? - условной 8 позиций (два кортежа)
    
    И 5 вариантов, который могут быть образованы двумя сочетаниями, который перебираете вручную
    
    ++++----
    
    -++++---
    
    --++++--
    
    ---++++-
    
    ----++++
    
    где "++++" - то, что мы ищем
    
    ibessonov Автор
    26.11.2023 20:20
    #26204428
    Так откуда матрица?
    
    Смотрите, если последним прочитанным кортежем был ??FU, то CK?? дальше читать "нельзя", если FUCK хотим исключить, а если последним был ?FUC, то "нельзя" читать K???. Вероятности разные для разных букв. Матрица как раз описывает вероятности перехода из одного состояния в другое.
    
    Никакого автомата нет, просто обработка идет сразу 4 символа за раз. И все.
    
    Автомат есть, но неявный. Есть пары кортежей, которые дают слово FUCK, есть которые не дают. Эти пары отвечают за разные рёбра в автомате, и за разные состояния, в том числе ими как-то должны определяться конечные состояния.
    
    Но прикол в том, что вероятность этого зависит от того что придет в ЭТОЙ четверке и предыдущей
    
    Всё верно, именно поэтому я написал, что вероятность там условная. И именно поэтому ваша формула неверна.
    
    Просто подставьте конкретные значения в вашу формулу и сравните с настоящим значением, которое можно получить (к примеру) полным перебором, или другим аналитическим способом (главное быть аккуратным).
    
    И получаеться в итоге обычная функция (1 - А)^N.
    
    Эту формулу легко опровергнуть. Если подставить N = 0, то мы должны получить вероятность, равную 0. У вас получается вероятность, равная 1. Если же подставить N = 1 (это число кортежей, верно?), то должно получиться 1/26^4. Верность данного значения, полагаю, никто не будет ставить под сомнение. Отсюда следовало бы, что A = 1-1/26^4.
    Далее, для N = 2 ваша формула даёт вероятность (1 - A)^2 = 1/26^8. Данная вероятность уже ни при каких условиях не может быть верной, поскольку она бы означала, что есть только одно слово из всех.
    Если попробовать повторить те же рассуждения с вашей более ранней формулой вида (1 - 1/26^4)(1 - A)^N, то возникают те же проблемы при подстановке 0, 1, 2 в качестве N.
    Проверка - важный этап вывода формулы, она может указать на закравшиеся ошибки.
    
    В статье я привёл значения, которые можно проверить с помощью ручки-бумаги. Это (например) вероятности для строки длины 0, 4 и 8. Они равны, соответственно, 0, 1/26^4 и 5/26^4 - 1/26^8. Моё предложение - подберите формулу, которая работала бы хотя-бы на этих трёх вариантах.
    Если вы считаете, что эти 3 числа неверны, то прошу обосновать, в чём на ваш взгляд у меня ошибка. Спасибо!
    
    Batalmv
    26.11.2023 20:20
    #26204590
    Ладно, задача ваша :)
    
    Итоговая формула (1-0.999997812)(1-8.75319E-06)^N, где N - число четверок
    
    Либо в красивом виде (1 - 1/26^4)(1 - 1/26^4 - (1/26^2)^2 - 2*(1/26*1/26^3))^N
    
    Явно видно, как ее можно растянуть на любое число символов с строке, которую генерим случайным образом :)
    
    Множители тоже понятны:
    
    зерно: 1 - 26^4
    
    вероятность выпадения FUCK в целой четверке итерации: 1/26^4
    
    вероятность склейки FU+CK: (1/26^2)^2
    
    вероятность склейки F+UCK и вероятность склейки FUC+K: 2*(1/26*1/26^3)
    
    Так как выпадение FUCK останавливает программу - мы считаем только вероятность продолжения, отнимая от 1 вероятность FUCK и перемножая с вероятностью предыдущей итерацией (так как чтобы попасть в эту, нам надо чтобы и до того FUCK не выпал)
    
    P.S. Таки налажал в предыдущем посте, но воспользовался советом и проверил формулу через тривиальные случаи. Теперь верная. Плюс криво в Excel ввел :)
    
    ibessonov Автор
    26.11.2023 20:20
    #26204686
    Моё предложение - подберите формулу, которая работала бы хотя-бы на этих трёх вариантах
    
    Так она на этих 3х вариантах работает? А на остальных?
1. sci_nov
  26.11.2023 20:20
  #26204424
  +1
  fuck головного мозга )))

michaelkuz
26.11.2023 20:20
#26204184
Теоретики

https://www.atractor.pt/fromPI/PIalphasearch-_en.html

Were found 265 occurrences of the word FUCK in the first 147999997 digits of π in base 27.

265/147999997=0.0000017905

P. S.

Нет, не подходит. Используется base 27, что добавляет пробел. И ищет слово с пробелами с двух сторон. Тоесть в нашем случаи " FUCK "

maxim_ge
26.11.2023 20:20
#26205004
А в чём проблема, интересно, вот такого варианта.
- В строке из 20 символов - 17 попыток набрать группу из 4 символов
- В каждой попытке вероятность получить группу 1 / 26 ^ 4, не получить (1 - 1 / 26 ^ 4)
- Не получить в 17 попытках: (1 - 1 / 26 ^ 4) ^ 17
- Получить хотя бы в одной попытке = 1 - не получить ни в одной = 1 - (1 - 1 / 26 ^ 4) ^ 17 = 0.00003720042
Вольфрам даёт 0.0000372004271441587940142843061796238205490663502391574596846357
1. ibessonov Автор
  26.11.2023 20:20
  #26205628
  Проблема в том, что для умножения вероятностей применяется лишь в конкретных случаях. Но это даже не важно, потому что вы, скорее всего, имели ввиду умножение на 17, а не возведение в 17-ю степень, то есть сумму вероятностей (это же подтверждает ваш ответ, не совпадающий с тем, что дала бы формула).
  Почти та же самая формула рассмотрена в статье, в разделе 2 про аппроксимацию. Под статьёй, в комментариях, было приведено множество дополнительных аргументов в пользу того, что аппроксимация неточная.
  Ваша же конкретная формула ошибочна по той же причине - вы складываете вероятности событий, которые пересекаются. В этом случае необходимо вычитать вероятности пересечения. Нельзя просто взять и умножить на 17, это так не работает :)
  1. maxim_ge
    26.11.2023 20:20
    #26206038
    Но это даже не важно, потому что вы, скорее всего, имели ввиду умножение на 17, а не возведение в 17-ю степень
    
    Нет, именно возведение в степень. Вероятность выбросить решку пять раз подряд 1/2^5. Вероятность появления орла в серии = 1 - 1/2^5 = 0.96875.
    
    это же подтверждает ваш ответ, не совпадающий с тем, что дала бы формула
    
    Тут ситуация обоюдоострая, возможно, таки, неверна формула. "Нетрудно понять..." - это сильное утверждение, но необязательно верное. Хотелось бы разобраться.
    
    вы складываете вероятности событий, которые пересекаются
    
    Но я не складываю вероятности.
    
    вы складываете вероятности событий, которые пересекаются.
    
    Тогда бы получилось "больше". А у меня - "меньше".
    
    ibessonov Автор
    26.11.2023 20:20
    #26206134
    +2
    Но я не складываю вероятности.
    
    Я затупил, извиняюсь, там действительно возведение в степень.
    Попробую объяснить, почему возведение в степень даёт неточный ответ. Формулу возведения в степень вы, я полагаю, взяли из схемы Бернулли (https://ru.wikipedia.org/wiki/Схема_Бернулли) как частный случай. Для того, чтобы схема Бернулли работала, у вас должна быть последовательность независимых событий.
    Цитирую: результат очередного эксперимента не должен зависеть от результатов предыдущих экспериментов.
    В случае же, когда вы движетесь по конкретному слову и проверяете его подслова, события являются зависимыми. Например, после прочтения слова FUCK, следующим словом для проверки будет UCK* - т.е. 100% не FUCK. Вероятность следующего события зависит от предыдущего события. Т.е. не соблюдены необходимые условия примения формулы. Надеюсь так яснее.
    Ещё раз извиняюсь за свой затуп в прошлом комментарии. Если говоришь кому-то, что он не прав, самому лучше не ошибаться :)
    
    maxim_ge
    26.11.2023 20:20
    #26206440
    Формулу возведения в степень вы, я полагаю, взяли из схемы Бернулли
    
    Будем так говорить, я её на листочке вывел по ходу дела, собственно, весь вывод повторён в моём комментарии.
    
    Например, после прочтения слова FUCK, следующим словом для проверки будет UCK* - т.е. 100% не FUCK. Вероятность следующего события зависит от предыдущего события.
    
    Да, так и есть????????

venanen
26.11.2023 20:20
#26205008
+1
А нельзя ли так рассуждать:
Если строка из 20 букв, а нам нужно искать слово FUCK в котором четыре буквы. Т.е. в крайнем случае строка будет из 5 слов FUCK подряд.
1) Нам известна вероятность встретить хотя-бы раз слово FUCK в строке.
2) Мы можем (можем же?) посчитать вероятность встретить слово FUCK два раза в строке, но так как 2 вхождения - включают в себя одиночное вхождение из предыдущего пункта, то из п.1 отнять вероятность встречи двух слов;
3) Так же как в п.2. Встретить три слова - это точно встретить два и точно встретить 1;
4) Так же как в п.3;
5) Так же как в пункте 4.
В результате ответ будет равен вычитанию из п.1 всех остальных вероятностей.
P.S. терверу я не очень близок, мягко говоря, просто интересно в чем я неправ.
1. ibessonov Автор
  26.11.2023 20:20
  #26205652
  Нам известна вероятность встретить хотя-бы раз слово FUCK в строке.
  
  Неизвестна, это именно та вероятность, которую я искал в статье, но допустим. Кажется вы поставили задачу "найти вероятность встретить FUCK ровно один раз".
  Её можно решать предложенным вами подходом, но очень сложно.
  
  Мы можем (можем же?) посчитать вероятность встретить слово FUCK два раза в строке
  
  Наверное? Повторюсь, кажется очень сложным.
  А вообще, согласно приведённой схеме, для того, чтобы посчитать вероятность вхождения ровно один раз, мы должны посчитать вероятность вхождения ровно два раза. Это кажется контринтуитивным, как будто решаем более сложную задачу ради более простой. Думаю, что такой путь никуда нас не приведёт.
  1. wataru
    26.11.2023 20:20
    #26206040
    +2
    Это как раз получается формула включения исключения. Итоговая формула будет:
    $\sum_{k=1}^{\lfloor n/4\rfloor}(-1)^{k+1} 26^{-4k} C_{n-3k}^{k}$
    Первое слагаемое - как у вас в приблизительной формуле - просто втыкаем одно слово из 4 букв в любую из n-3 позиций, а оставшиеся буквы берем как угодно. Но так строки с двумя вхождениями посчитаются по 2 раза. Поэтому мы их вычтем во втором слагаемом. Третье слагаемое прибавляет назад строки с тремя вхождениями, которые вычлись слишком много раз и т.д. Внутри слагаемого у нас сочетание из n-3k по k - Можно представить что у нас есть n-3k символов и мы должны к k из них сделать 'f' приписать к ним "uck". Так переберутся все возможные варианты расстановки нескольких слов в строке. Это можно тут делать, потому что два вхождения строки "fuck" не могут пересекаться никак. Для какой-нибудь "abacaba" - эта формула уже неработает.
    
    Edit:
    
    wolframalpha насчитал для n=20: 0.0000372006426280718997290310967979713483574288305450310306335572
    
    ibessonov Автор
    26.11.2023 20:20
    #26206182
    В такой формулировке гораздо понятнее, спасибо!
    Да, этой формуле мне противопоставить нечего, она выглядит совершенно верной.
    
    ibessonov Автор
    26.11.2023 20:20
    #26206306
    Блин, не сразу заметил, что это сообщения от двух разных людей. То то я и думал, что-то не стыкуется немного стиль оформления и размышления) Мне нужно быть внимательнее

MichaelSkirda
26.11.2023 20:20
#26211724
+1
А если слово вроде fuf? Оно может быть как концом первого слова так и началом другого.
fufuf -> 2 fuf
1. ibessonov Автор
  26.11.2023 20:20
  #26211734
  Про такие слова в статье есть информация, но уже ближе к концу. Рекуррентное соотношение в том виде, в каком оно дано в начале, для fuf строить нельзя, вы правы