Качество переходного процесса ч.2 / forpes.ru

Главная
Качество переходного процесса ч.2

Качество переходного процесса ч.2

14.01.2024 21:15

petuhoff 4 1300 Источник

Продолжаем публикацию Олега Степановича Козлова. Кафедра "Ядерные энергетические установки" МГТУ им. Н.Э. Баумана. В предыдущих сериях:

1. Введение в теорию автоматического управления.2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.

3. Частотные характеристики звеньев и систем автоматического управления регулирования. 3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.

4. Структурные преобразования систем автоматического регулирования.

5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).

6. Устойчивость систем автоматического регулирования. 6.1 Понятие об устойчивости САР. Теорема Ляпунова. 6.2 Необходимые условия устойчивости линейных и линеаризованных САР. 6.3 Алгебраический критерий устойчивости Гурвица. 6.4 Частотный критерий устойчивости Михайлова. 6.5 Критерий Найквиста.

7. Точность систем автоматического управления. Часть 1 и Часть 2

8. Точность систем автоматического управления. Часть 1

8.5 Обобщающее соотношение по связи частотных свойств замкнуто САР с переходным процессом (без вывода)

В предыдущей части был были выведены формулы описывающие связь переходного процесса с частотными характеристиками замкнутой САР, в этом разделе приведем основные соотношения:

Переходный процесс через мнимую часть $Q(\omega)$ :

$y(t)=P(0)+\frac{2}{\pi}\int_0^\infty\frac{Q(\omega)}{\omega}cos (\omega)d\omega$

Переходный процесс через вещественную часть $P(\omega)$ :

$y(t)=\frac{2}{\pi}\int_0^\infty\frac{P(\omega)}{\omega}sin(\omega\cdot t)d\omega$

Свойства линейности:

если $P(\omega)=\sum_{j=1}^mP_j(\omega),$ то

$h_j(t)=\frac{2}{\pi}\int_0^\infty\frac{P_i(\omega)}{\omega}\sin(\omega\cdot t)d\omega\Rightarrow y(t)=\sum_{j=1}^mh_j(t)$

Соответствие по оси ординат:

$a\cdot y(t)=\frac{2}{\pi}\int_0^\infty\frac{a\cdot P(\omega)}{\omega}sin(\omega\cdot t)d\omega$
Соответствие по оси абсцисс:

$y\left(\frac{t}{a}\right)=\frac{2}{\pi}\int_0^\infty\frac{P(a\cdot\omega)}{\omega}cos(\omega\cdot t)d\omega$
Предельные соотношения:

$\lim_{\omega\rightarrow0}P(\omega)\equiv P(0)=\lim_{t\rightarrow0}y(t)=y_\infty\equiv y_{уст}$

$\lim_{\omega\rightarrow\infty}P(\omega)=\lim_{t\rightarrow0}y(t)=y(t)$
Вид переходного процесса в зависимость от вида вещественной части части АФЧХ

a) Если $P(\omega)>0$ и производная $\frac{dP(\omega)}{d\omega}\le0$ , то перхоодной процесс - колебательный.

Рисунок 8.5.2 Вид монотонной зависимости вещественной части АФЧХ

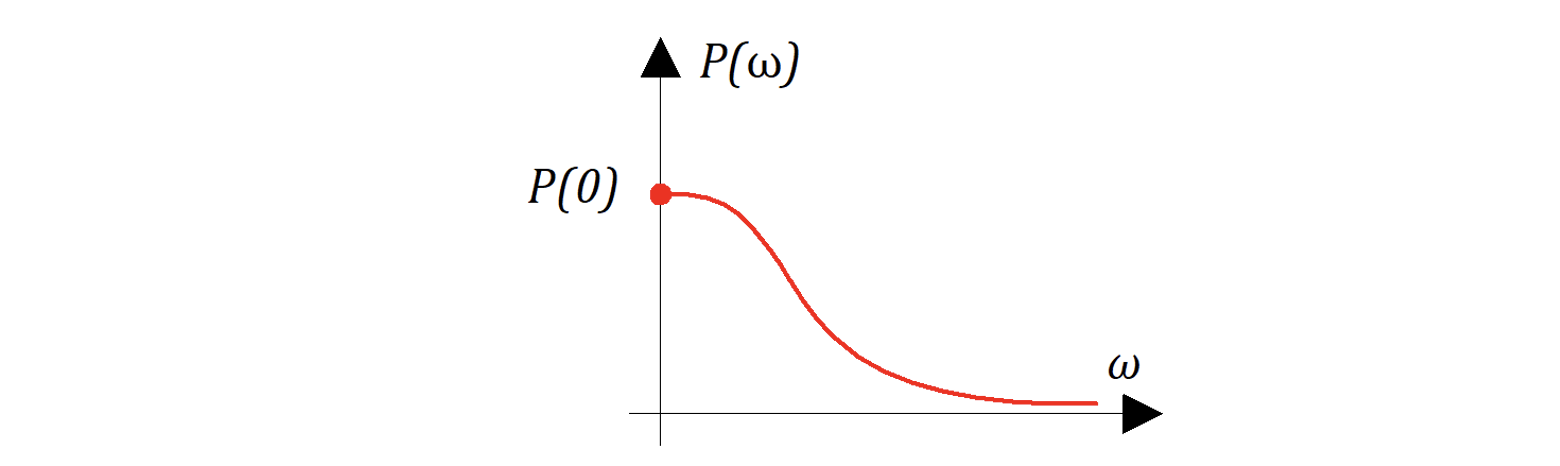
б) Если $P(\omega)>0$ и производная $\frac{dP(\omega)}{d\omega}<0$ , то переходный процесс монотонно убывающий.

в) Если $P(\omega)=const$ при $\omega<\omega^*$ и $P(\omega)=0$ при $\omega\ge\omega^*$ (ступенчатая функция разобранная в п.8.4), то колебательный перходной процесс с перерегулированием, максимальное отклонение $\sigma=0.18$

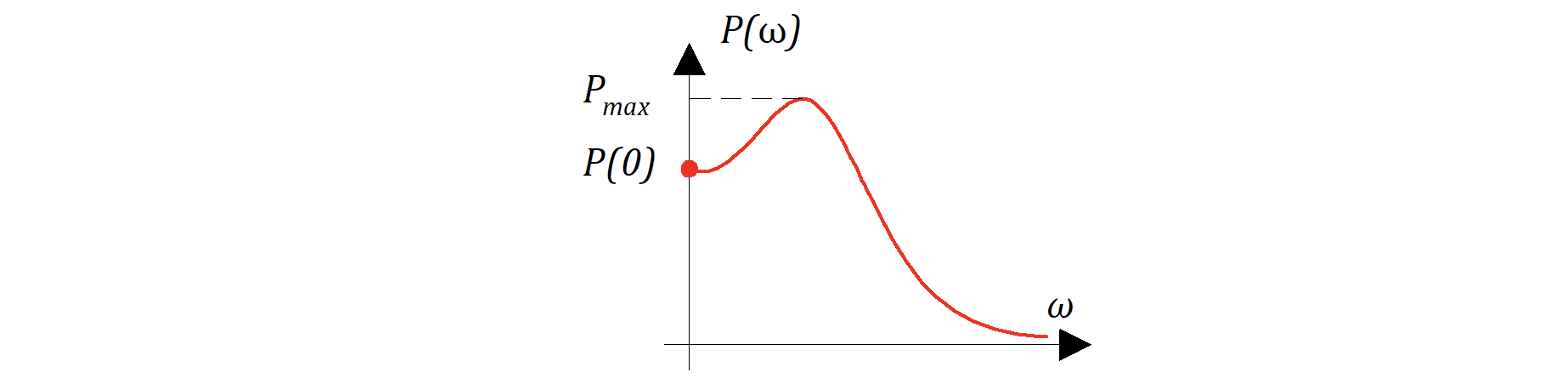
г) Если $P(\omega)$ имеет "горб", как на рисунке 8.5.3, то максимальное отклонение $\sigma\ge0.18$

Рисунок 8.5.3 Вид зависимости вещественной части АФЧХ с "горбом"

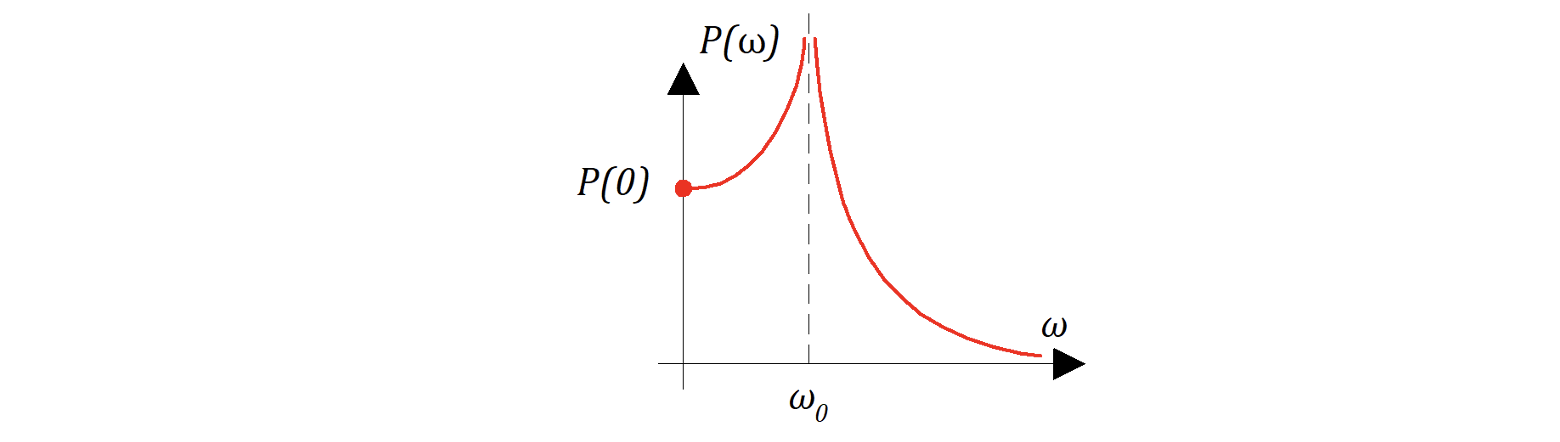
д) Если $P(\omega)$ имеет «разрыв» как на рисунке 8.5.4 то в САР устанавливаются незатухающие колебания с частотой.

Рисунок 8.5.4 Вид зависимости вещественной части АФЧХ с разрывом

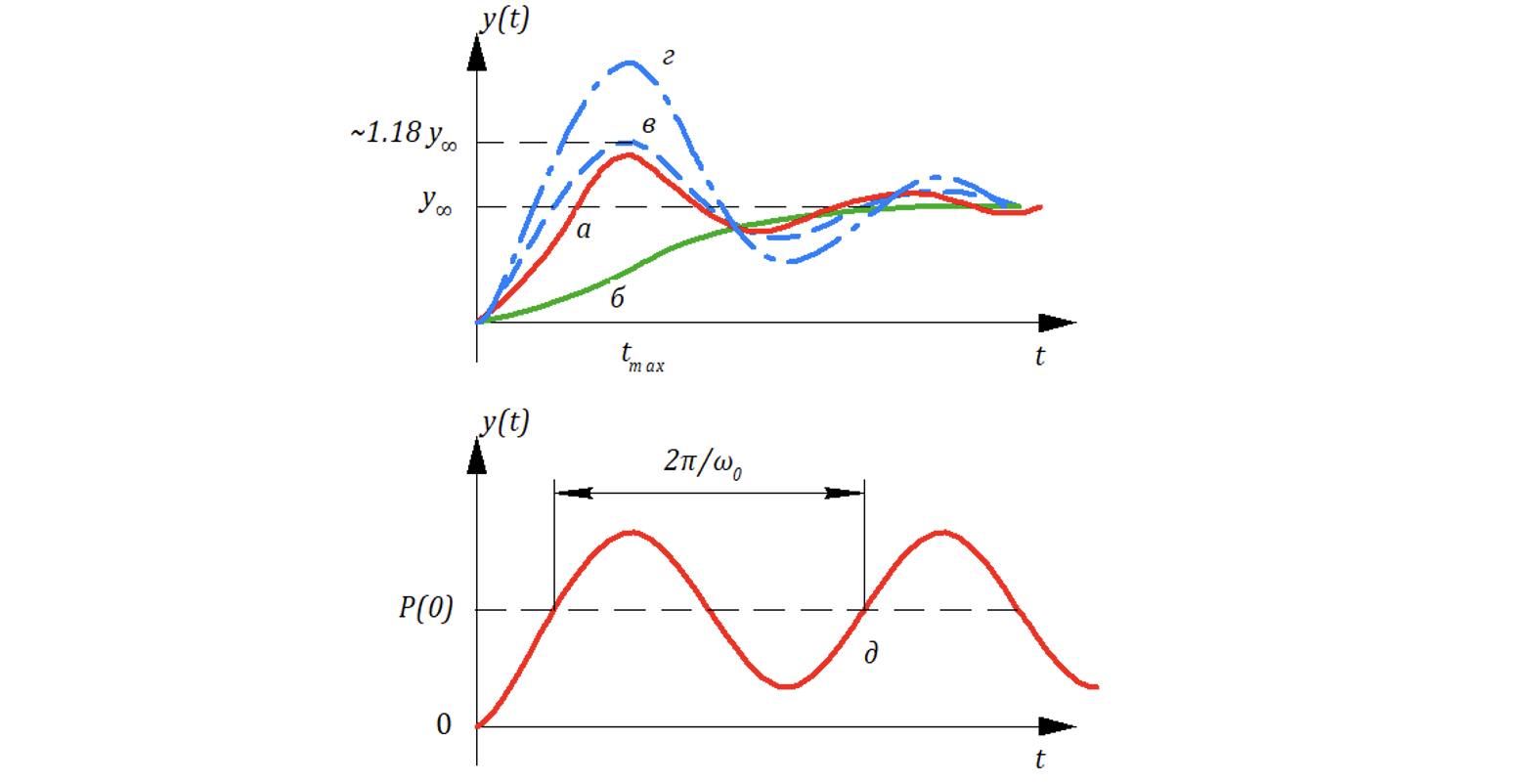
Обобщающие графики переходного процесса имеют вид:

Вещественная часть АФЧХ $P(\omega)$ близка к трапецеидальной, (см. рис. 8.5.6)

Рисунок 8.5.6 Веществанная часть АФЧХ близкая к трапецидальной

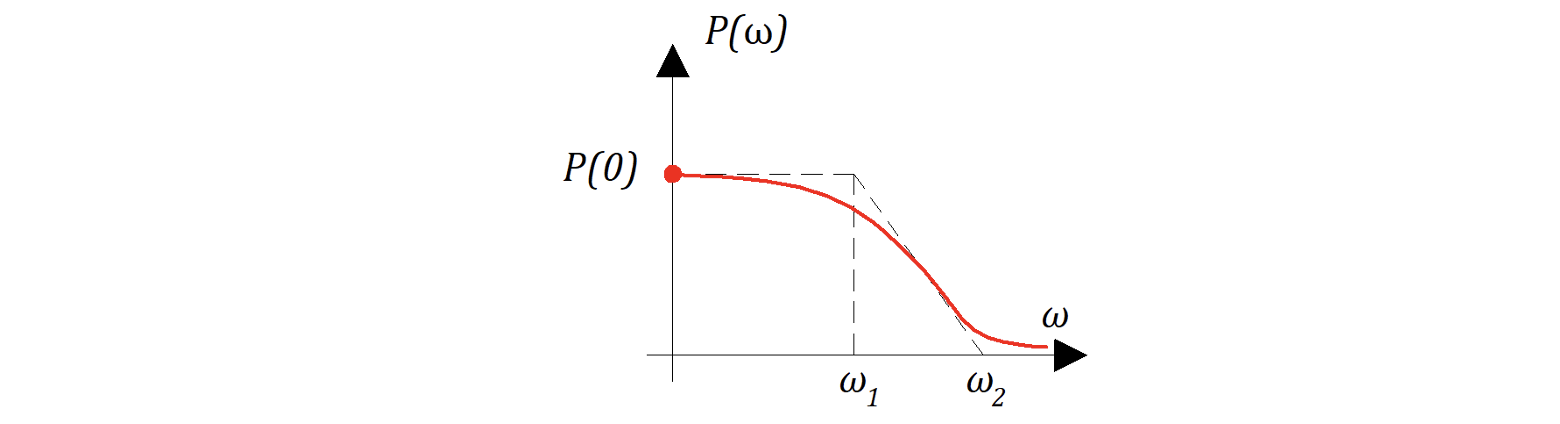
Такой вид АФЧХ позволяет определить примерное время переходного процесса $T_{пп}$ :

$\frac{\pi}{\omega_2}<T_{пп}<\frac{4\cdot\pi}{\omega_1}$

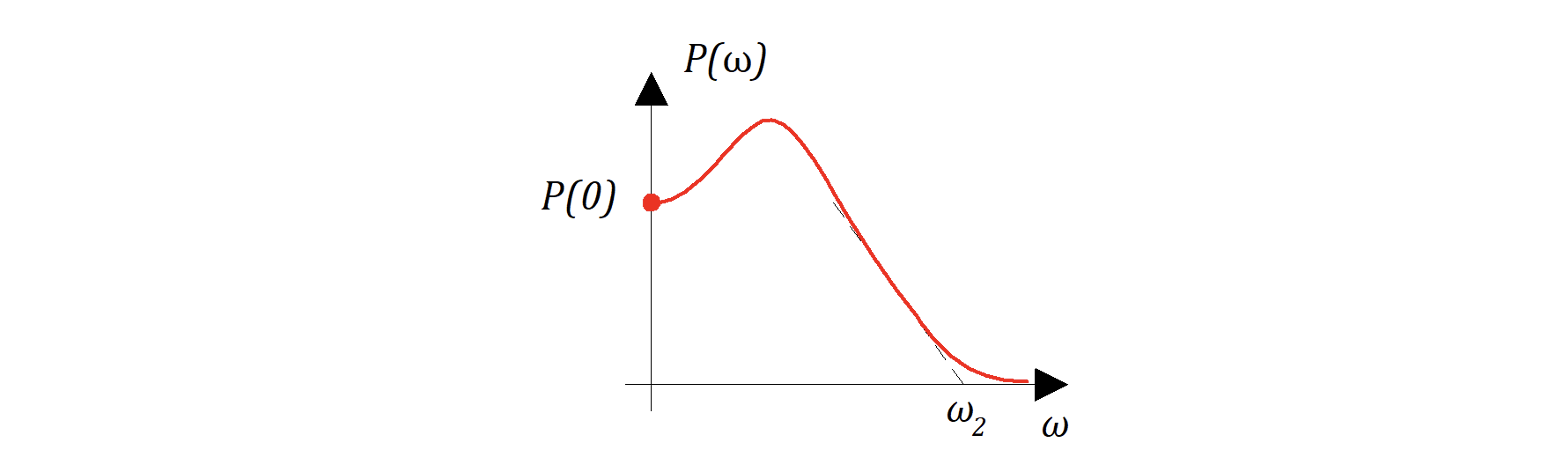
Вещественная часть АФЧХ $P(\omega)$ имеет горб (см. рис. 8.5.7). Время переходного процесса $T_{пп}$ можно оценить используя $\omega_2$ - пересечение касательной или интервал положительности.

Рисунок 8.5.7 Вещественная часть с горбом

$\frac{3\pi}{\omega_2}<T_{пп}<\frac{4\pi}{\omega_2}$

8.6 Метод корневого годографа (Метод Эванса)

Хотя метод корневого годографа и не относится непосредственно к корневым методам оценки качества переходного процесса, тем не менее в комбинации с прямыми корневыми оценками переходного процесса (см. следующие подразделы) метод корневого годографа позволяет расширить анализ (и синтез) САР...

В «классической» формулировке, предложенной Эвансом, рассматривается замкнутая САР (см. рисунок 8.6.1) и необходимо определить «траектории» корней характеристического уравнения замкнутой САР в зависимости от К – коэффициента усиления разомкнутой САР.

Рисунок 8.6.1. Схема САР для метода Эванса

Передаточная функция замкнутой САР: $D(s)=L(s)+k\cdot N(s)$

Характеристическое уравнение замкнутой САР:

$D(\lambda)=L(\lambda)+k\cdot N(\lambda) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.6.1)}$

Если $k=0\Rightarrow$ Характеристическое уравнение замкнутой становится эквивалнетно характеристическому уравнению разомкнутой САР: $D(\lambda)\equiv L(\lambda)$

Следовательно ветви корневого годографа начинаются в полюсах разомкнутой САР.

Если $k\rightarrow\infty$ , то ветви корневого годографа заканчиваются либо в нулях главной передаточной функции (т.е. в точках, где $N(\lambda)=0$ ), либо в бесконечности (как вещественной, так и комплексной).

Пример:

Рассмотрим САР представленные на рисунке 8.6.2

Характерестическое уравнение $D(\lambda)=\lambda\cdot(\lambda+1)\cdot(\lambda+2)\cdot(\lambda+3)+k\cdot(\lambda+0.5)=0$ ;

Очевидно, что если , $\lambda_1=0;\ \ \lambda_2=-1; \ \ \lambda_3=-2; \ \ \lambda_4=-3;$ то то есть корни уравнения совпадают с полюсами разомкнутой САР.

Рисунок 8.6.3 Траектория корней характерестического уравнения

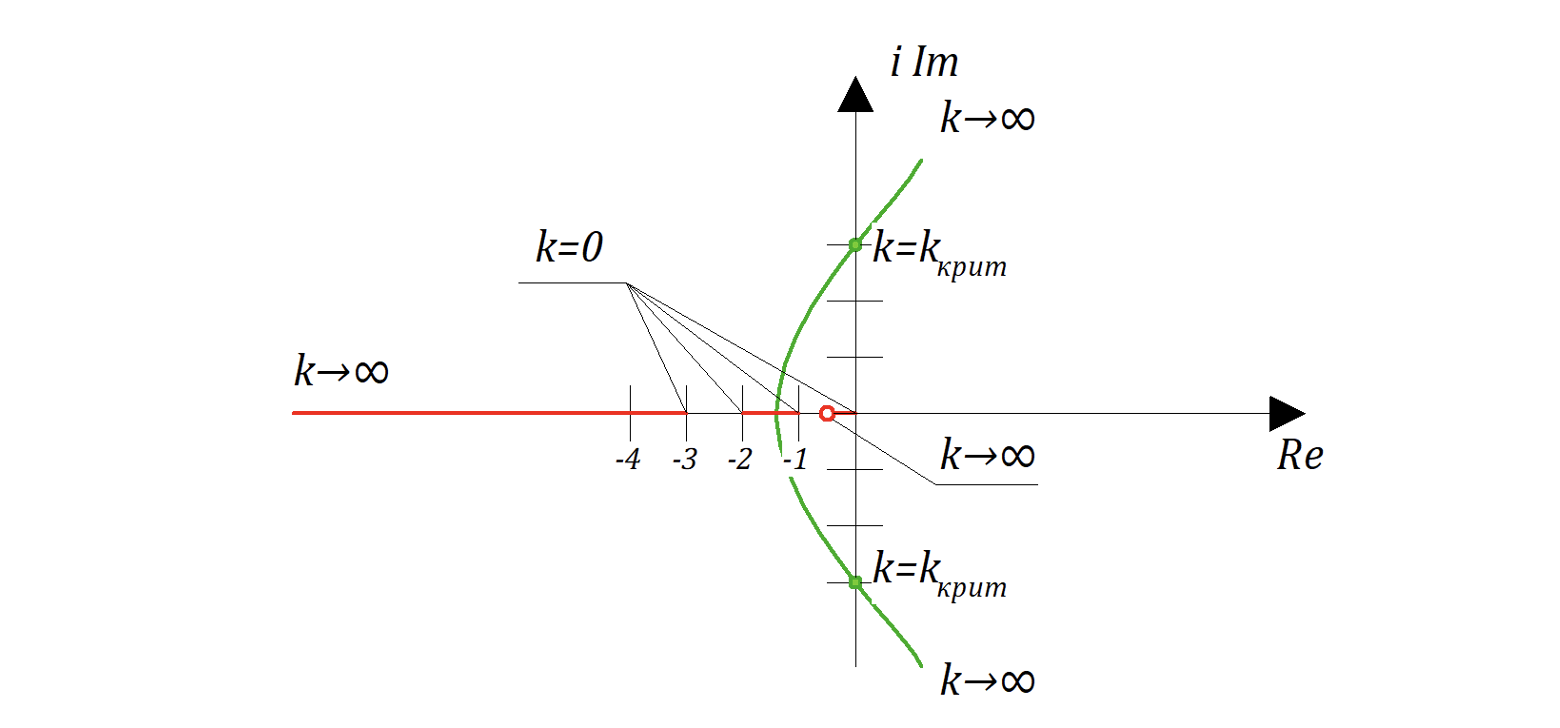
Замкнутая система является устойчивой, если её полюса лежат в левой полуплоскости плоскости корней. Соответственно при пересечении ветвями годографа мнимой оси слева направо система из устойчивой становится неустойчивой. Коэффициент усиления, соответствующий этому переходу, называется критическим. Данное свойство полезно при оценке устойчивости системы.

8.7 Корневые методы оценки качества переходного процесса.

Вид переходного процесса при заданном законе изменения внешнего воздействия (управляющего) определяется передаточной функцией системы или матрицами А, В, С, D (для систем, описываемых в переменных «вход-выход» или в переменных состояния, соответственно).

Если система описывается в переменных «вход-выход»:

$W(s)=\frac{k\cdot N(s)}{L(s)}$ - передаточная функция разомкнутой САР.

$\Phi(s)=\frac{W(s)}{1+W(s)}$ - передаточная функция замкнутой САР.

Переходный процесс определяется в первую очередь полиномом $D(s)=L(s)+k\cdot N(s)$ , хотя вид полинома - далеко не безразличен, т.е. влияют и знаменатель и числитель передатояной функции $\Phi(s)$ .

Если в главной передаточной функции $\Phi(s)$ полином вырождается в константу (т.е. ), то переходный процесс определяется только знаменателем, т.е. расположением корней характеристического уравнения:

$D(\lambda)=a_n\cdot\lambda^n+a_{n-1}\cdot \lambda^{n-1}+...+a_1\cdot\lambda+a_0=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.7.1)}$

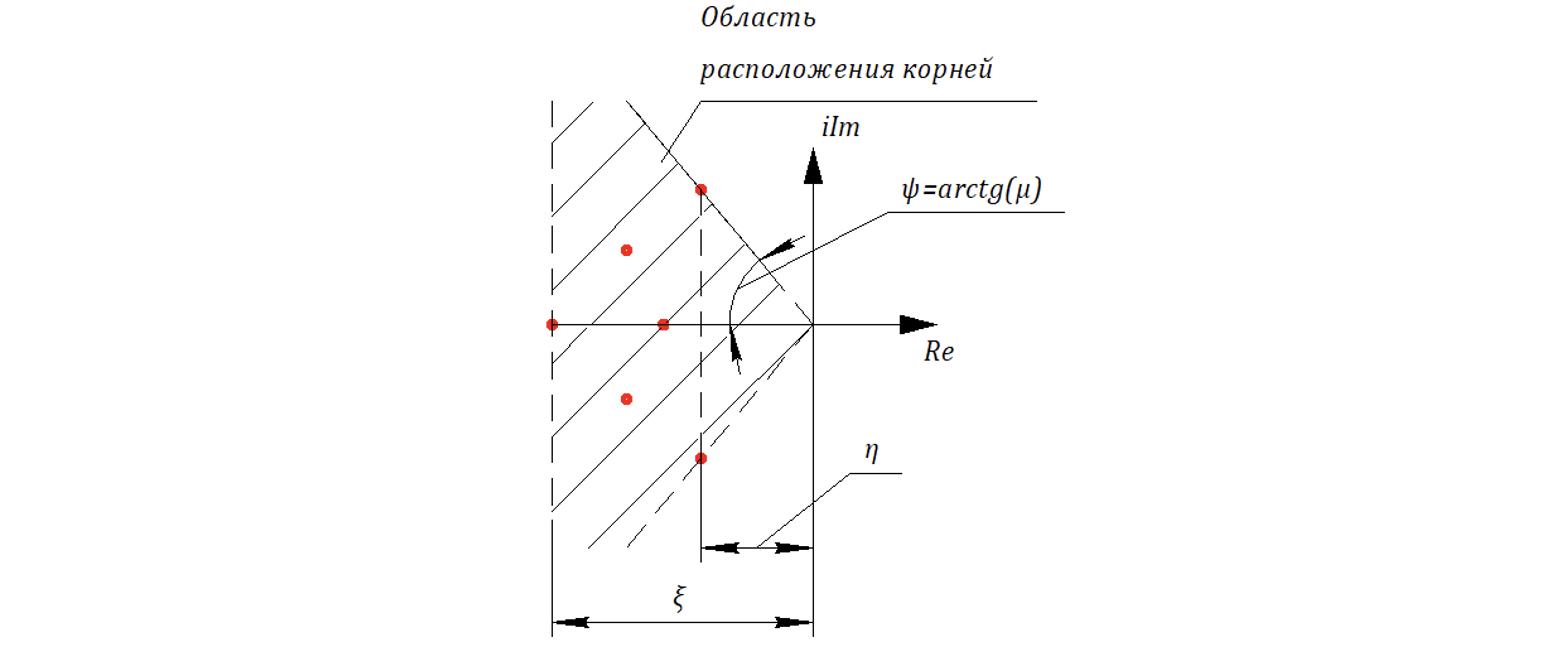
Область расположения корней $\lambda_i$ на комплексной плоскости можно характеризовать тремя показателями:

$\eta$ - степень устойчивости или минимальным удалением корня от мнимой оси $\eta=|Re \ ( \lambda_i)|_{min}$
$\mu$ - колебательность, $\mu=|tg(\Psi)|_{max}$ (см. рисунок 8.7.1) $\mu=\left| \frac{\beta}{\alpha}\right |_{max}$ где $\alpha,\beta$ -вещественная и минимая часть корня $\lambda_j=-\alpha_j+i\cdot \beta_j$
$\xi$ -степенью удаленности корня от мнимой оси $\xi=|Re(\lambda)|_{max}$

Напомним, что $y(t)_{coбст.}=\sum_{j=1}^{n}c_j\cdot e^{\lambda_j\cdot t}$ (если нет совпадающих корней)

Рисунок 8.7.1 Показатели качества переходного процесса на коплесной полоскости

Степень устойчивости $\eta$ . Характеризует быстроту окончания переходных процессов: чем больше $\eta$ , тем быстрее должна регулируемая величина с заданной точностью достигать своего установившегося значения.

Необходимо отметить, что понятие «степень устойчивости» имеет к понятию «устойчивость» зачастую меньшее отношение чем колебательность $\mu$ .

Более точно, колебательность $\mu$ в большей степени связана с запасом устойчивости (по фазе и амплитуде). Чем меньше $\mu$ , тем запасы устойчивости (по фазе и амплитуде) больше.

Степень удаленности $\xi$ характеризует наиболее быстро-затухающие составляющие переходного процесса.

В теории управления часто оперируют (используют) понятием «жесткость» системы: $G=\frac{\xi}{\eta}$

Чем больше , тем больше «проблем» при численном решении задачи, т.к. явные разностные численные схемы могут стать неустойчивыми в математическом смысле.

В реакторных САР параметр жесткости обычно высок:

- в реакторах на тепловых нейтронах (РБМК, ВВЭР и т.д.)

- в промежуточных реакторах (реакторы на промежуточных нейтронах), реакторы космических ЯЭУ, транспортные реакторы.

- реакторы на быстрых нейтронах (БН-350, БН-600, БН-800, БОР-60).

Для решения очень жестких задач используют специальные разностные явные алгоритмы или неявные (полунеявные) разностные алгоритмы, например метод Гира, а так же методы Леонида Марковича Скворцова.

Необходимо еще раз отметить, что понятие «степень устойчивости» не связано в явном виде с удалением от границы устойчивости (по фазе и амплитуде), т.е. с запасом по фазе и амплитуде.

Запас устойчивости зависит от колебательности САР. Вместо колебательности $\mu$ зачастую используется другой показатель – затухание за период.

При наличии комплексных корней:

$y_{соб}(t)=\sum_j^nc_j\cdot e^{\lambda_j\cdot t}\Rightarrow y_{соб}^j(t)=c_j\cdot e^{-\alpha_j\cdot t}\cdot sin(\beta_j\cdot t+\varphi_j) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.7.2)}$

где: $С_j,-\alpha_j, \ \beta_j$ - амплитуда, вещественная и мнимая части доминирующего корня $\lambda_j=-\alpha_j+i\cdot \beta_j$ , тогда период $T_j=2\cdot\pi/\beta_j$

Запишем решение при :

$y_{coб}^j(t_1)=c_j\cdot e^{-\alpha_j\cdot t_1}sin(\beta_j\cdot t_1+\varphi_j)\Rightarrow\\ \Rightarrow A_j=c_j\cdot e^{-\alpha_j\cdot t}\Rightarrow A(t_1)=c_j\cdot e^{-\alpha_j\cdot t_1}$

Тогда время через период: $t=t_1+T_j=t_1+\frac{2\cdot \pi}{\beta_j}$

Запишем решение через период:

$y_{соб}^j(t_1+T)=c_j\cdot e^{-\alpha_j\cdot(t_1+T)}sin(\beta_j(t_1+T)+\varphi_j)\Rightarrow\\A(t_1+T)=c_j\cdot e^{-\alpha_j\cdot t_1}\cdot e^{-\alpha_j\cdot T}=C_j\cdot e^{-\alpha_j}\cdot e^{-\alpha_j\frac{2\pi}{\beta_j}}=\frac{1}{\mu}$

Затухание за период: $\xi=\frac{A(t_1)-A(t_1+T)}{A(t_1)}=1-\frac{A(t_1+T)}{A(t_1)}\Rightarrow$

$\xi=1-e^{-2\pi/\mu}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.7.3)}$ $\mu=\frac{2\pi}{ln\left (\frac{1}{1-\xi} \right)}=-\frac{2\pi}{ln(1-\xi)}\ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.7.4)}$

Если затухание за период составляет 0.9, то $\mu=2.72$ , а если $\xi=0.98$ (затухание 98%), то $\mu=1.57$ .

Таким образом, чем меньше колебательность $\mu$ , тем больше затухание $\xi$ за один период и тем больше запас устойчивости.

Один из наиболее простых способов синтеза САР с заданной степенью $\eta$ устойчивости основан на использовании метода Д-разбиения, причем на плоскости одного комплексного параметра его формулировка и правила совпадают с рассмотренным ранее «классическим» вариантом Д-разбиения.

Если имеем замкнутую САР и ее характерестическое уравнение:

$D(\lambda)=a_n\cdot \lambda^n+a_{n-1}\cdot\lambda^{n-1}+...+a_1\cdot\lambda+a_0=0 \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.7.2)}$

Предположим, что мы желаем, чтобы все корни характеристического уравнения лежали (находились) левее прямой $Re=-\eta$

Рисунок 8.7.2 Области корней характеристического уравнения

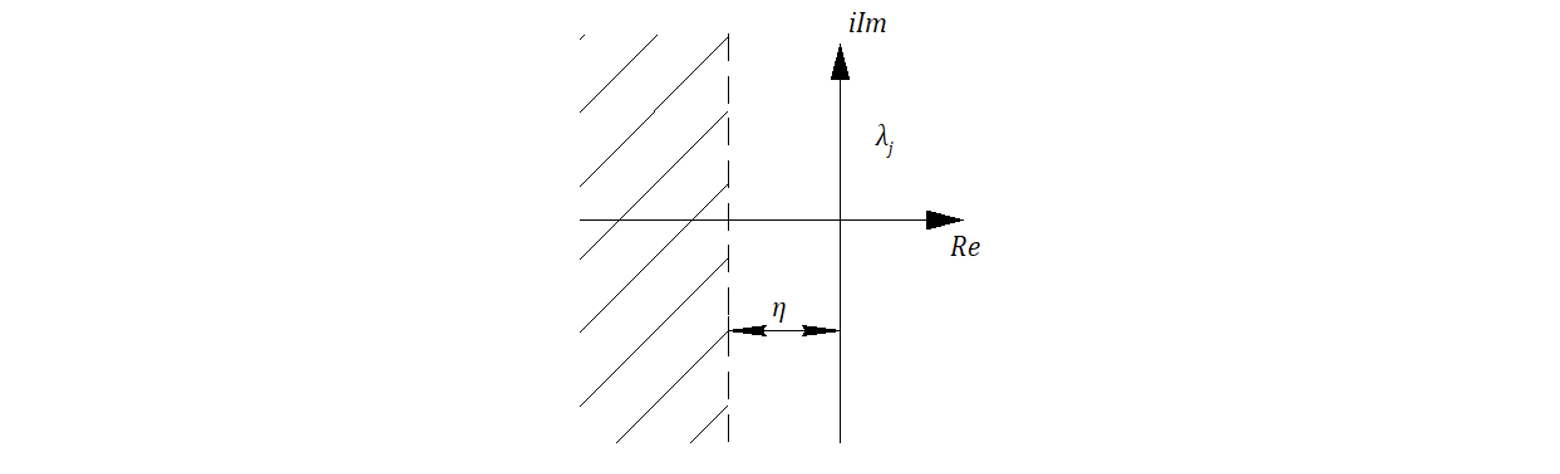
Предположим, что имеется возможность варьировать какой-то параметр САР (например коэффициент усиления какого-то звена k или какую-то постоянную времени Т).

Предполагая, что k входит в коэффициенты характеристического уравнения линейным образом, по аналогии с «классическим» (см. лекцию 6) случаем имеем:

$k=\frac{S(\lambda)}{R(\lambda)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{(8.7.3)}$

Поскольку мы желаем, чтобы корни лежали левее прямой $Re=-\eta$ , необходимо в (8.7.3) вместо $\lambda$ подставить $(-\eta)$ . $\lambda=-\eta+i\cdot\omega$ - такая подстановка означает, что какой-то корень характеристического уравнения лежит на пунктирной прямой (см. рисунок). Тогда линия Д-разбиения принимает вид:

Рисунок 8.7.3 Изменение области D-разбиения

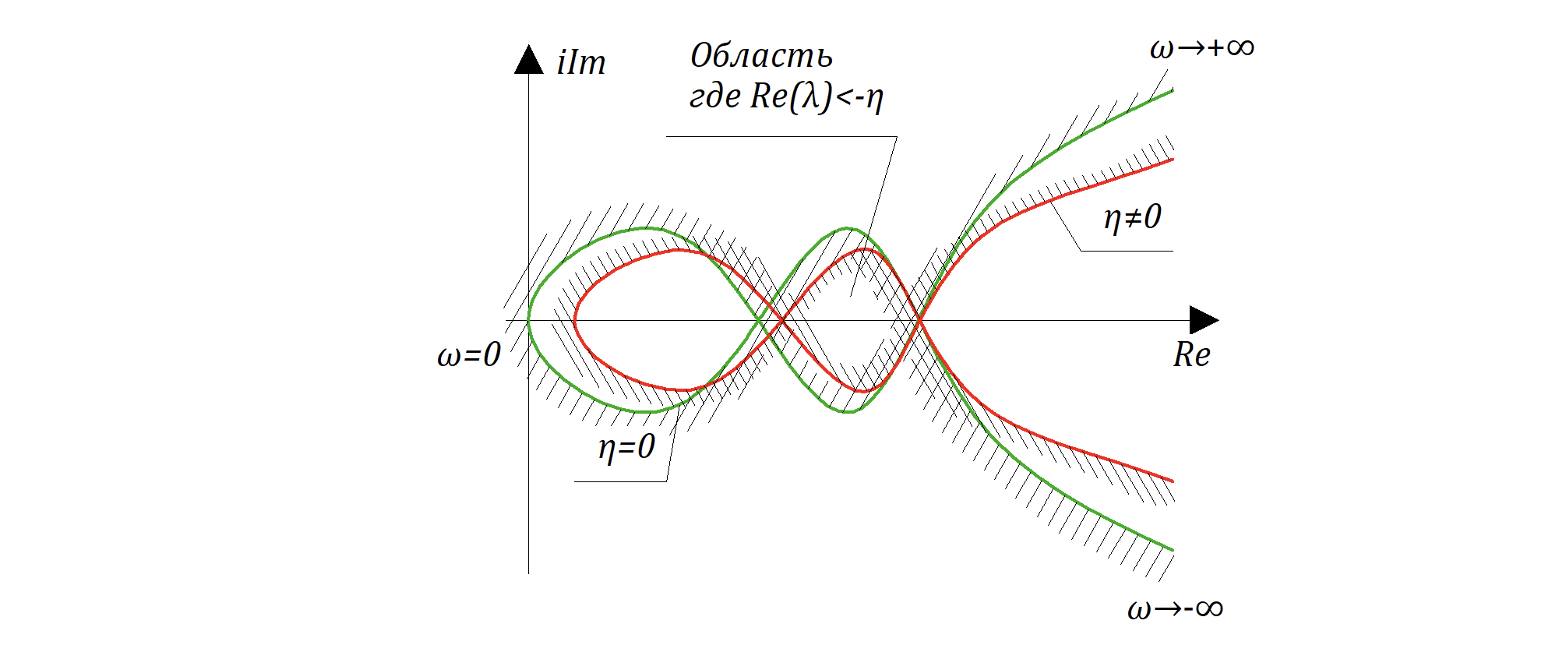
Необходимо подчеркнуть (отметить), что приведенные выше соображения полностью корректны (справедливы), если многочлен в передаточной функции замкнутой САР

$\Phi(s) = \frac{k\cdot N(s)}{D(s)}$ вырождается в const:

В этом случае вид переходного процесса однозначно определяется расположением $\Phi(s)$ полюсов (или корней характеристического уравнения $D(\lambda)=0$ ).

Если все полюса (корни) вещественны (т.е. мнимая часть = 0) и различны, то переходный процесс будет монотонным:

Рисунок 8.7.4 Монотонный перехоодной процесс

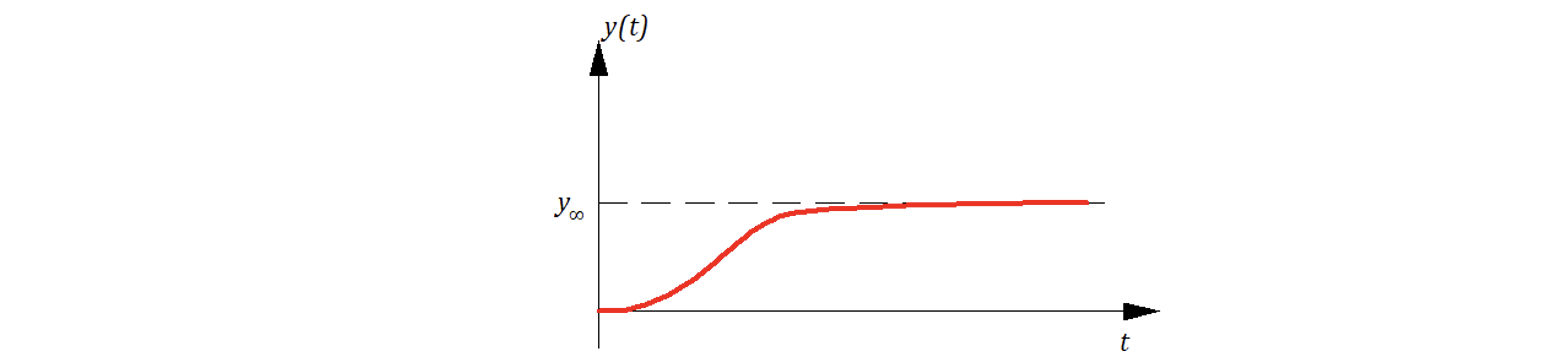
Если все полюса (корни) вещественны и есть совпадающие, то зачастую переходный процесс проходит с небольшим перерегулированием:

Рисунок 8.7.5 Переходной процесс с перерегулированием

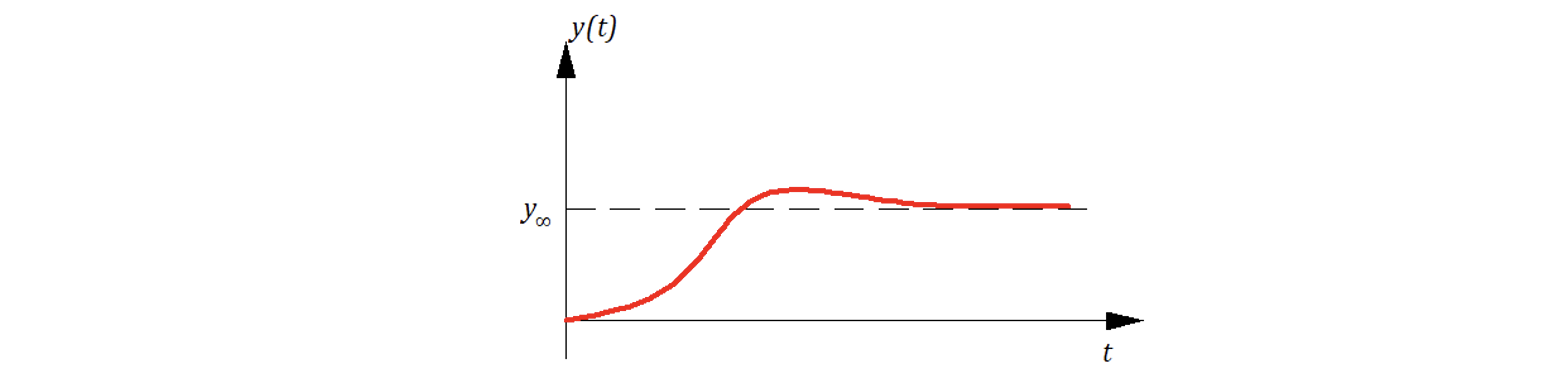
Если имеются и чисто вещественные и комплексные полюса (корни), то характер переходного процесса определяется доминирующим полюсом, т.е. полюсом, имеющим наибольшую (алгебраически) вещественную часть, т.е. полюсом (корнем), наиболее близко расположенным к мнимой оси.

Если доминирующий корень – вещественный, то переходный процесс будет близок к апериодическому (квазимонотонный) – кривая 1, а если доминирующий корень комплексный, то переходный процесс зачастую имеет колебательный характер (с перерегулированием) – кривая 2 (см. рисунок ниже).

Рисунок 8.7.6 Кривые переходные процессы в зависмости от доминирующего корня

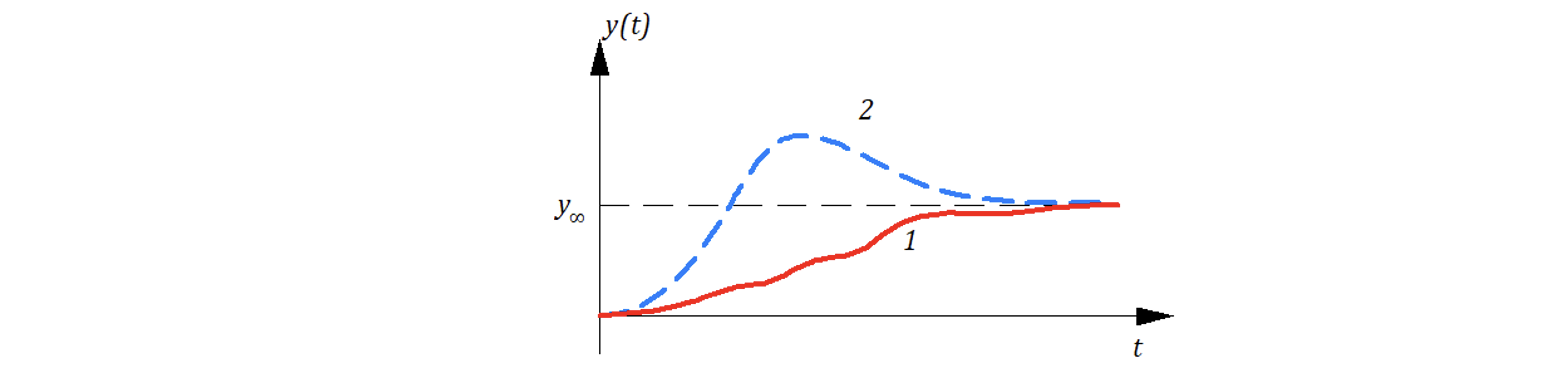
Если $N(s)\ne const$ , то характер переходного процесса будет зависеть не только от расположения полюсов (корней), но и от расположения нулей полинома .

Наличие нулей в передаточной функции $\Phi(s)$ приводит к тому, что при всех вещественных несовпадающих полюсах (корнях характеристического уравнения) переходный процесс в САР может иметь несколько колебаний относительно установившегося значения, т.е. наличие нулей может нарушить условие апериодичности (монотонности) переходного процесса.

Наиболее ярко влияние нулей на колебательный характер переходного процесса проявляется в тех случаях, когда нули и полюса (корни) расположены относительно далеко друг от друга.

Пример 1

Сравнить переходные процессы двух САР с одинаковыми характерестическии уравнениями и разными знаменателями.

$\Phi_1(s)=\frac{N_1(s)}{L(s)}=\frac{2\cdot s^2+1.1\cdot s+4}{(s+1)(2\cdot s^2+s+4)}$ $\Phi_2(s)=\frac{N_2(s)}{L(s)}=\frac{8\cdot s^2+s+4}{(s+1)(2\cdot s^2+s+4)}$

Полюсса харктеристического уравнения САР: $s_1=-1, s_{2,3}=-0,25\pm i\cdot\frac{\sqrt{31}}{4}$

Нули передаточной функции для $\Phi_1$ : $P'_{1,2}=-\frac{1.1}{4}\pm\frac{\sqrt{31}}{4}\cdot i\approx-0.275\pm1.4\cdot i$

Нули передаточной функции для $\Phi_2%$ : $P_{1,2}''=-\frac{1}{16}\pm\frac{\sqrt{127}}{16}\approx-0.0625\pm0.7\cdot i$

Рисунок 8.7.7 Переходной процесс и расположение нулей и корней

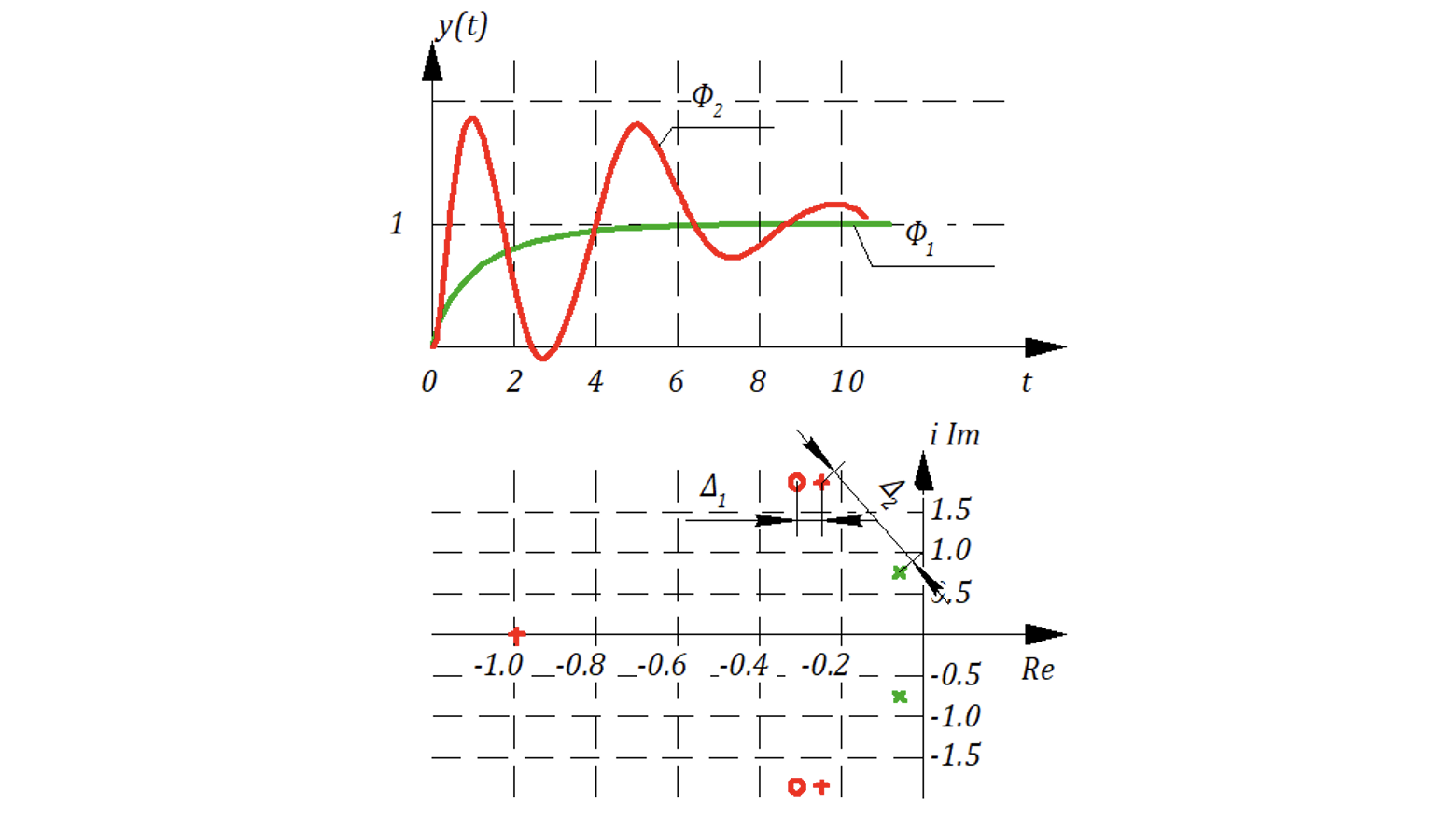
Строим струкутурные схемы и моделируем единичное ступенчатое воздействие в SimInTech

Рисунок 8.7.8 Моделирование САР в SimInTech

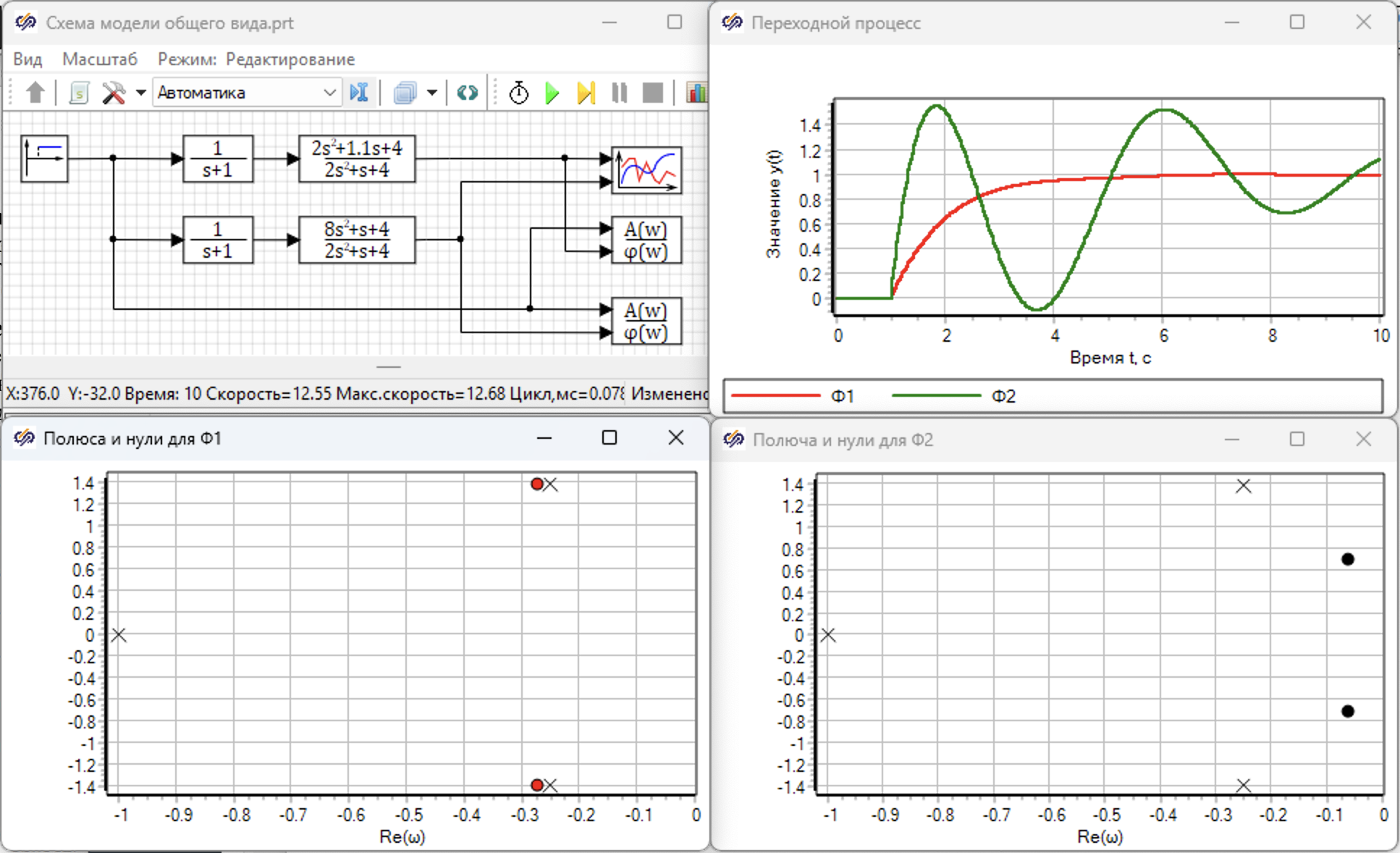
Пример 2

Определить пределы изменения , при которых простейшая САР ядерного реактора (см. рис. 8.7.9) обеспечивает степень устойчивости $\eta=0.5, 1, 0$ .

Рисунок 8.7.9 Модель САР ядерного регулирования

Праметры модели САР ядерного реактора:

$l=5\cdot10^{-4} с$ -время жизни мгновенных нейтронов;
$\sigma=-3\cdot10^{-4};$ -обратная связь между мощностью и реактивностью;
$\beta=0.007$ - эфективная доля запаздывающих нейтронов;
$\lambda =0.072 [1/c];$ -постоянная распада ядер-предшественников;
$T=0.15 \ \ c.$ - постоянная времени привода управления;
$u_0=5 \ \beta$ - эфективность стержня управления.

В данной САР варьируемым параметром является коэффициент усиления привода .

$\Phi(s)=\frac{W_1\cdot W_{экв}}{1+W_1\cdot W_{экв}}$ $W_{экв}=\frac{W_2}{1-W_{oc}\cdot W_2}=\frac{s+\lambda}{s(l\cdot s+\beta)+\sigma(s+\lambda)}=\frac{s+\lambda}{l\cdot s^2+(\beta+\sigma)\cdot s+\sigma\cdot \lambda}$ $\Phi(s)=\cfrac{k\cdot u_0(s+\lambda)}{s(T s+1)\left[1+\cfrac{k\cdot u_0}{s(T s+1)}\cdot\cfrac{s+\lambda}{l s^2+(\beta+\sigma) s+\sigma\lambda}\right ](l s^2+(\beta+\sigma)s+\sigma\lambda)}$ $\Phi(s)=\frac{k\cdot u_0(s+\lambda)}{Tls^4+[l+T(\beta+\sigma)]s^3+[\sigma\lambda T+\beta+\sigma]s^2+(\sigma\lambda+k\cdot u_0)s+k\cdot u_0\lambda}$

Учитывая, что в данном случае постоянная распада ядер-предшественников запаздывающих нейтронов по форме записи совпадает с обозначением корня характеристического уравнения, найдем полюса:

$D(s)=Tls^4+[l+T(\beta+\sigma)]s^3+[\sigma\lambda T+\beta+\sigma]s^2+(\sigma\lambda+ku_0)s+ku_0\lambda=0$ $k=-\frac{Tls^4+[l+T(\beta+\sigma)]s^3+[\sigma\lambda T+\beta+\sigma]s^2+\sigma\lambda s}{u_0(s+\lambda)}$

Подставляя вместо s значения 1: $s=-0.5+i\omega$ , 2: $s=-1+i\omega$

Получаем следующие графики:

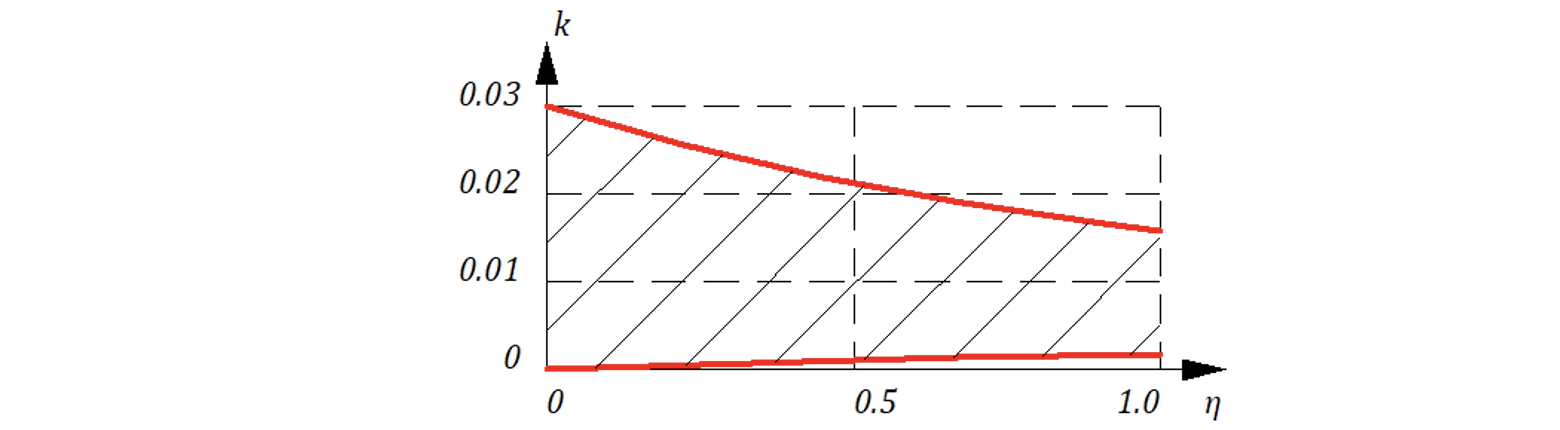
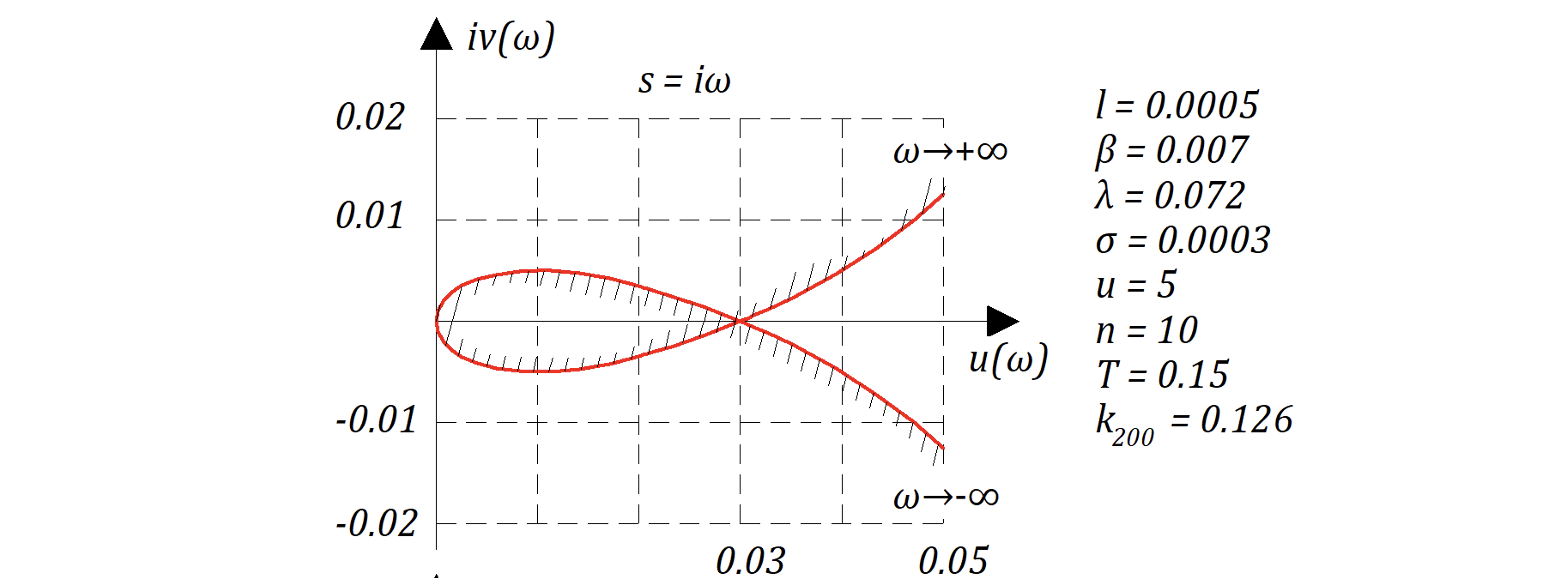
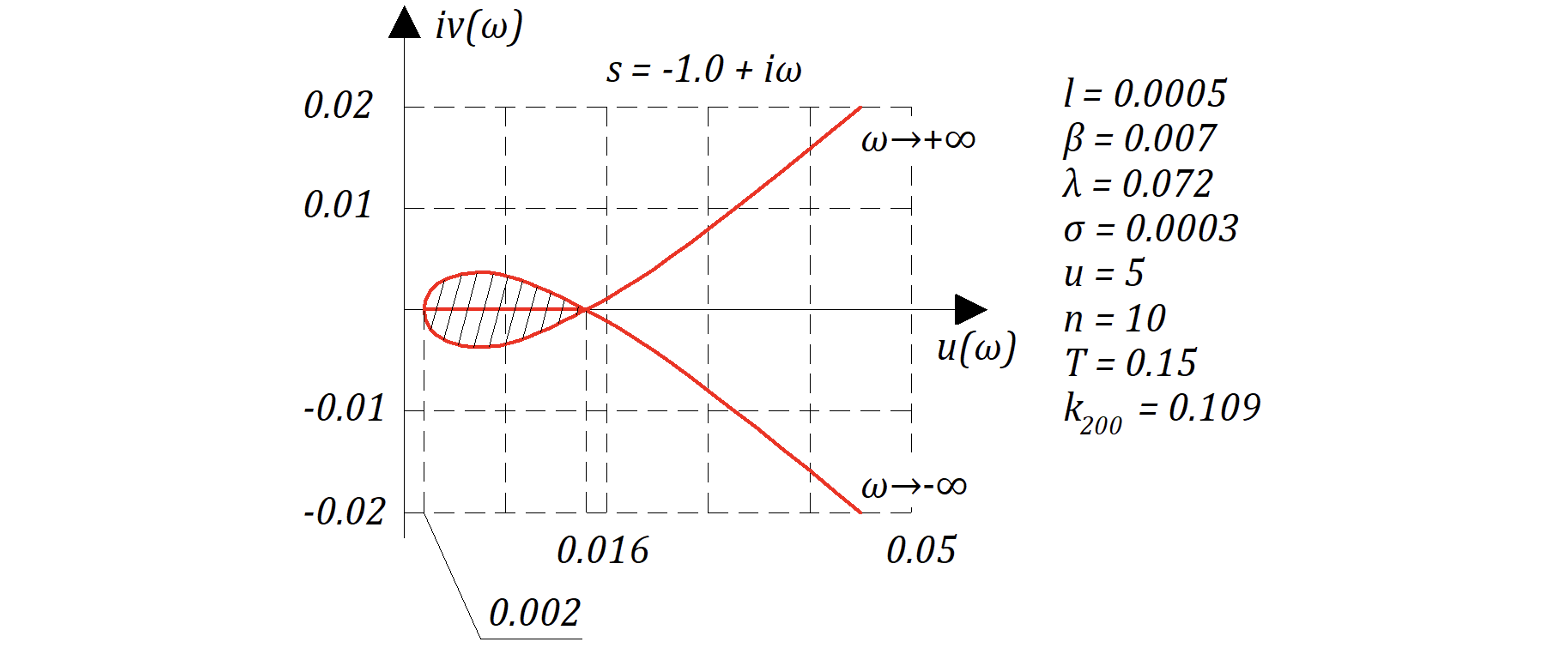
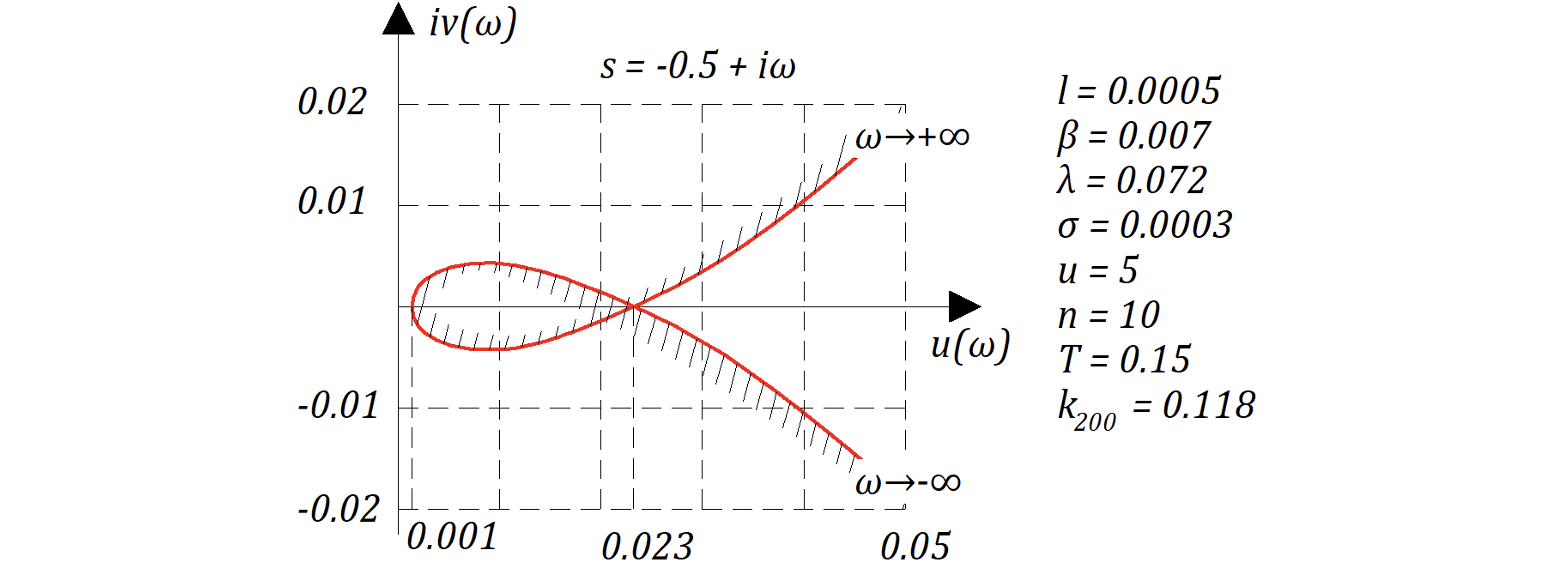
Второе видео получилось случайной, Mодель реактора в SimInTech при настройках системы по умолчанию считает хуже чем карандаш и бумага!

Модели из лекции можно взять здесь...

Комментарии (4)

igord1960
15.01.2024 11:08
#26380240
В начале описка: "Если $P(\omega)$ имеет "гроб"". Наверное, имелось в виду: "горб".
1. petuhoff Автор
  15.01.2024 11:08
  #26380262
  спасибо поправил

YetAnotherJip
15.01.2024 11:08
#26380260
Спасибо. Кажется, в оглавлении последних нескольких ваших статей потерялась ссылка на раздел 6.6 Понятие об областях устойчивости https://habr.com/ru/articles/732448/ .
1. petuhoff Автор
  15.01.2024 11:08
  #26380268
  да в некторых оглавлениях почему то сбой будем разбираться