Алгоритм генерации столбцов (Column Generation) / forpes.ru

Главная
Алгоритм генерации столбцов (Column Generation)

Алгоритм генерации столбцов (Column Generation)

22.03.2024 12:08

Lozkins 0 1500 Источник

Генерация столбцов - подход к решению задач смешанного линейного программирования (MIP) с большим кол-вом переменных или столбцов.

В статье представил теоретическую предпосылку, схему алгоритма и python реализацию подхода. В практической части рассмотрел решение двух задач: задача планирования расписания и задача раскроя.

Математическая база

Погружение в алгоритм генерации столбцов начнем с симплекс метода. Описание всего симплекс метода оставлю за рамками этой статьи, здесь рассмотрим только его этап - определение ведущего столбца для добавления в базис (pricing problem).

Вектор приведенной стоимости (reduced cost)

Пусть имеем задачу линейного программирования в канонической форме. Для определенности рассмотрим задачу минимизации:

$\begin{align}\min cx \\Ax = b & & (1)\\x \in \mathbb{R}^{m+} & & \\\end{align}$

где - вектор коэффициентов целевой функции размерности , - вектор вещественных переменных размерности , и - матрица коэффициентов при ограничениях и вектор свободных членов соответственно.

Определения: Пусть $(B \quad N)$ - разбиение столбцов матрицы таким образом, что имеет размерность $m \times m$ и определитель матрицы отличен от нуля. Тогда $x = (x_B \quad x_N)$ и $c=(c_B \quad c_N)$ - соответствующее разбиение для и . Будем называть допустимое решение x = (x_B, x_N) - базисным (основным), если x_N = 0 . Переменные x_B называются базисными (основными) переменными, а x_N - свободными.

В процессе решения задачи линейного программирования, на каждой итерации симплекс метода происходит оценка (pricing) свободных переменных и выбор нового кандидата для добавления в базис (ведущий столбец). Этот шаг играет ключевую роль в алгоритме генерации столбцов, как и в самом симплекс методе.

$Ax = (B \quad N)\begin{pmatrix} x_B \\ 0\end{pmatrix} = b, \text{ => } x_B = B^{-1}b.$

Если является допустимым базисным решением, тогда значение целевой функции (стоимость) будет:

$cx = (c_B \quad c_N)\begin{pmatrix} x_B \\ 0\end{pmatrix} = c_BB^{-1}b.$

Куда уйти с текущей угловой точки (текущего базисного решения), чтобы улучшить целевую функцию? Предположим, что свободные переменные теперь могут принимать не нулевые значения, обозначим такой вектор $x' = (x'_B \quad x'_N)$ , тогда

$Ax' = (B \quad N)\begin{pmatrix} x'_B \\ x'_N\end{pmatrix} = b.$

Домножим правую и левую часть на $B^{-1}$

$B^{-1}Ax' = (I \quad B^{-1}N)\begin{pmatrix} x'_B \\ x'_N\end{pmatrix} = B^{-1}b,$ $x'_B + B^{-1}Nx'_N = B^{-1}b,$ $x'_B = B^{-1}b - B^{-1}Nx'_N.$

Подставим значения вектора в целевую функцию:

$cx'= c_Bx'_B+c_Nx'_N = c_B(B^{-1}b - B^{-1}Nx'_N) + c_Nx'_N = c_BB^{-1}b + (c_N - c_BB^{-1}N)x'_N.$

Теперь рассмотрим вектор изменения целевой функции при допущении, что свободные переменные не равны нулю. Запишем изменение целевой функции как cx' - cx , что будет соответствовать

$c_BB^{-1}b + (c_N - c_BB^{-1}N)x'_N - c_BB^{-1}b= (c_N-c_BB^{-1}N)x'_N.$

Мы можем видеть, что если x_N увеличивается ( $x_N \ge 0$ ), функция затрат растет или убывает в зависимости от знака

$\bar{c} = c_N-c_BB^{-1}N.$

Вектор $\bar{c}$ называют приведенной стоимостью (reduced cost). Если существует отрицательная компонента в векторе $\bar{c}$ , то соответствующая ей свободная переменная может уменьшить значение целевой функции; добавляем её в базис.

В симплекс методе в базис добавляется одна переменная с наиболее отрицательной компонентой $\bar{c}$ , т.к. она осуществляет наискорейшее уменьшение целевой функции. Если в векторе $\bar{c}$ нет отрицательных компонент, то мы не можем улучшить целевую функцию, следовательно, мы нашли оптимальное решение.

На этом закончим погружение в симплекс метод и перейдем к алгоритму генерации столбцов.

Усеченная задача и генерация столбцов

Рассмотрим задачу смешанного линейного программирования (MIP) в стандартной форме следующего вида:

$\begin{align}\min \sum_{j \in J} c_{j} x_{j} \\\sum_{j \in J} \textbf{a}_j x_j \ge \textbf{b} & & (2)\\x_{j} \in \mathbb{R}^+|\mathbb{N}^+ & \quad \forall j \in J & \\\end{align}$

Будем называть задачу (2) основной (координирующей) сокращенно MP (Master Problem). Размерность задачи |J|=n столбцов (переменных) и $|\textbf{b}|=m$ строк (ограничений). Предполагается, что кол-во переменных в задаче экспоненциально больше кол-ва ограничений ( $n \gg m$ ). Здесь c_j - коэффициенты при переменных в целевой функции, x_j - решающие переменные, матрица коэффициентов при ограничениях $A=\{\textbf{a}_1, \dots, \textbf{a}_n\}$ и вектор свободных членов $\textbf{b}$ .

Расслабленной задачей к задаче (2) будем называть задачу с ослабленным ограничением на целочисленность переменных, т.е. в такой задаче все переменные являются целочисленными. Двойственная задача к прямой расслабленной задаче (2) запишется следующим образом:

$\begin{align}\max \textbf{u}^\intercal \textbf{b} \\\textbf{u}^\intercal A \le \textbf{c} & & (3)\\\textbf{u} \in \mathbb{R}^m & & \\\end{align}$

здесь $\textbf{u}$ - вектор двойственных переменных размерности .

Приведенная стоимость через двойственные переменные

Когда обсуждали вектор приведенной стоимости уже получали выражение $x_B = B^{-1}b$ для базисных переменных. Для этого базисного решения можем сформулировать соответствующую двойственную задачу: $B^\intercal u = c_B^\intercal$ . Применим операцию транспонирования к правой и левой частям равенства, домножим на $B^{-1}$ справа: $u^\intercal = c_B B^{-1}$ . Подставим полученный результат в формулу расчета приведенной стоимости (reduced cost), получим:

$\bar{c} = c_N-c_BB^{-1}N=c_N-u^\intercal N.$

Пусть $J_N = \{j_1, \dots, j_{n-m}\}$ -ьмножество индексов столбцов матрицы , которые соответствуют индексам свободных переменных и составляют матрицу . По симплекс методу добавляем в базис переменную, которая имеет самую отрицательную компоненту $\bar{c}_j$ из небазисных переменных, т.е.

$j_B = \text{arg} \min \{\bar{c_j} = c_j-u^\intercal a_j|j \in J_N\}$

Вполне правомерным можно назвать использование вместо J_N множество всех столбцов . Это оправдывается тем, что reduced cost для базисных переменных равен нулю: $c_B-c_BB^{-1}B = 0$ . Отвязываемся от деления матрицы на базисную и свободную часть:

$j_B = \text{arg} \min \{\bar{c_j} = c_j-u^\intercal a_j|j \in J\}.$

Ранее предполагали, что кол-во строк в матрице значительно меньше кол-ва столбцов. Громоздкость матрицы усложняет вычисления. На практике достаточно решить значительно меньшую задачу для получения того же оптимального решения.

Идея алгоритма генерации столбцов

Рассмотрим некоторую подзадачу (Restricted Master Problem, RMP) исходной задачи $J' \subset J$ при ( $|J'| \ge m$ ), которые отличаются между собой только кол-вом столбцов в матрице . Воспользуемся идеей симплекс метода добавления ведущего столбца в базис (pricing problem), но будем добавлять столбец в RMP. Таким образом, если для всех оставшихся столбцов приведенная стоимость (reduced cost) $\bar{c_j} \ge 0, \forall j \in J \text{\\} J'$ , то значение целевой функции RMP улучшить невозможно за счет добавления новых столбцов. Это означает, что в данном случае оптимальное решение подзадачи RMP и полной задачи MP совпадают.

Комментарий: Для расчета $\bar{c_j}$ в RMP используем $\bar{u}$ - вектор оптимальных значений двойственных переменных расслабленной задачи RMP.

Явное и неявное задание столбцов

Обратим внимание на множество столбцов , которое ранее предполагали получать в явном виде - определенный конечный набор столбцов. В некоторых задачах множество столбцов может быть безумно большим или бесконечным (например, столбцы могут описывать все возможные маршруты, паттерны, подмножества или перестановки). В этом случае можно попробовать прибегнуть к неявному способу задания множества столбцов через набор ограничений $a_j \in \mathcal{A}$ . Тогда поиск столбца будет сводится к оптимизационной задаче:

$\min \{c(a) - \bar{u}^\intercal a| a \in \mathcal{A} \}.$

Базовым примером применения такого множества ограничений $\mathcal{A}$ является задача оптимального раскроя, где a_j представляет собой паттерн разреза, а ограничения $\mathcal{A}$ с целевой функцией приведенной стоимости представляют собой задачу о рюкзаке. На каждой итерации алгоритма генерации столбцов решаем задачу о рюкзаке для построения паттерна. Затем добавляем этот паттерн в RMP.

Схема алгоритма

Зафиксируем основные этапы алгоритма генерации столбцов. Приведу для случая явного задания столбцов:

Фиксируем начальный набор столбцов для инициализации алгоритма;
Формулируем расслабленную задачу RMP. В исходной матрице и векторе оставляем столбцы, соответствующие зафиксированному набору столбцов ;
Строим двойственную задачу к RMP и решаем ее;
Pricing problem. Рассчитываем приведенную стоимость (reduced cost) и выбираем кандидата для добавления в RMP. Критерий: $j_B = \text{arg} \min \{\bar{c_j} = c_j-u^\intercal \textbf{a}_j|j \in J\}.$
Проверяем условия:
5.1. Если приведенная стоимость (reduced cost) для кандидата из п.4 - отрицательная, то добавляем его в и переходим в п.2.;
5.2. Если приведенная стоимость для $\forall j \in J$ неотрицательная, то останавливаем алгоритм (stop). Оптимальное решение RMP будет совпадать с оптимальным решением полной задачи MP;
Решаем прямую задачу RMP (на множестве столбцов ) с учетом целочисленности переменных. Полученное решение является оптимальным.

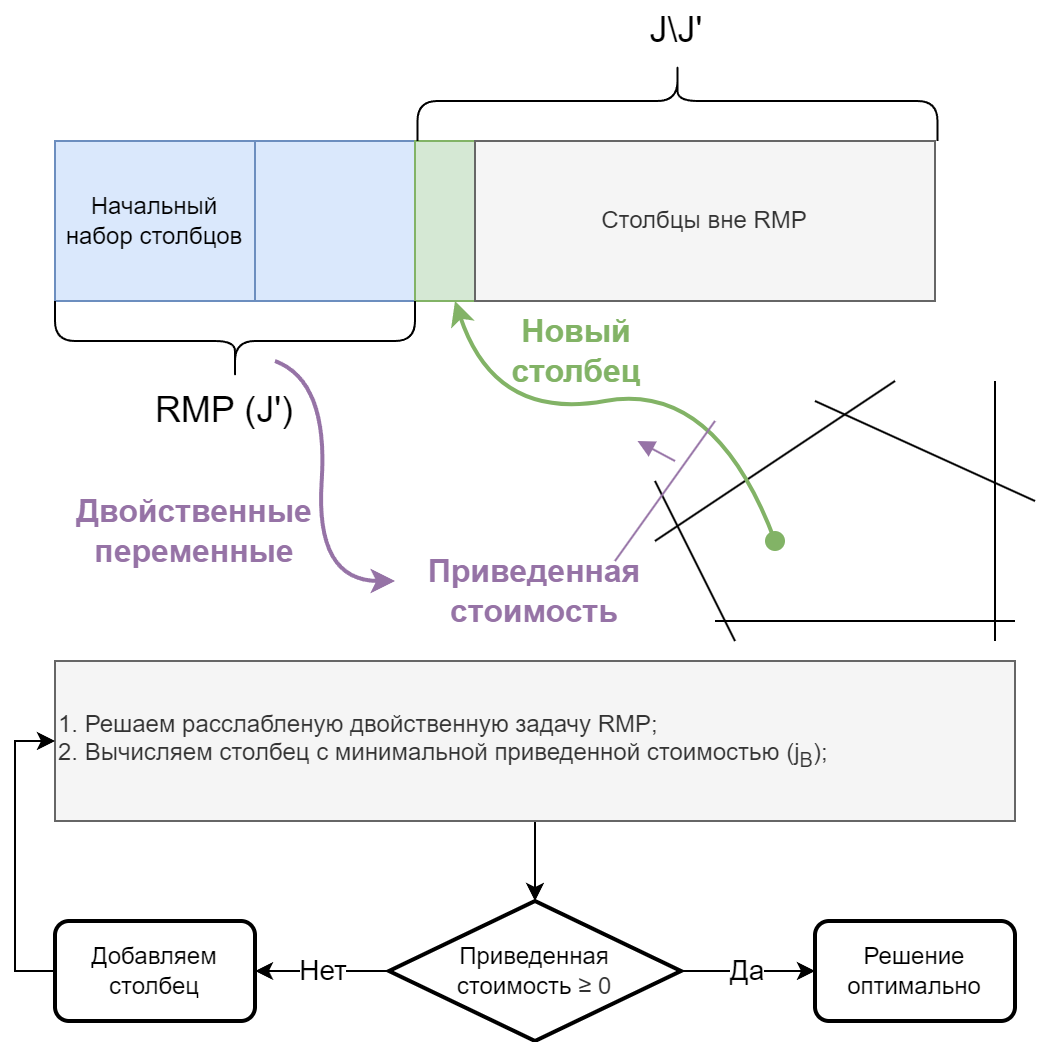
Дополнительным критерием остановки алгоритма рекомендую добавлять условие J = J' . В случае, когда все столбцы добавлены в RMP, мы получаем полную исходную задачу. Этот сценарий должен вызывать сомнение в корректности реализации алгоритма или его неприменимости к решению задачи в общем.

Практическая реализация

В технической части статьи рассмотрим 2 случая использования алгоритма генерации столбцов. В первом случае множество столбцов задается в явном виде, для реалистичности примера будем решать задачу планирования сменных графиков экипажей поездов в пассажира-перевозках. Второй случай: столбцы заданы в неявном виде через набор ограничений, речь пойдет о задаче раскроя.

По стеку технологий: python, ortools, солверы SCIP и GLOP, для работы с данными - numpy.

Задача планирования смен экипажей в пассажира-перевозках

Метод генерации столбцов широко используется для решения задачи планирования смен экипажей (Crew Scheduling Problem, CSP), особенно актуально в сфере ЖД пассажира-перевозок. Конечно, это далеко не единственная задача, где уместно применять метод генерации столбцов. Здесь с большим успехом можно также рассмотреть задачи о назначениях, задачи покрытия, задачи маршрутизации или др.

Задача заключается в планировании графиков работы экипажей на заранее известном наборе рейсов. На входе имеем план работ в виде участков движения поездов откуда-куда, время начала движения по участку, требования к квалификации экипажа или его составу и т.д. Цель задачи - найти минимальный набор экипажей, который обеспечит выполнение всех запланированных рейсов.

Одним из вариантов моделирования задачи является ее представление в виде задачи покрытия. На вход модели подаются готовые варианты графиков работы экипажей (допустимые), а результатом является выбор минимального кол-ва таких графиков (соответствует кол-ву экипажей), которые покрывают все рейсы.

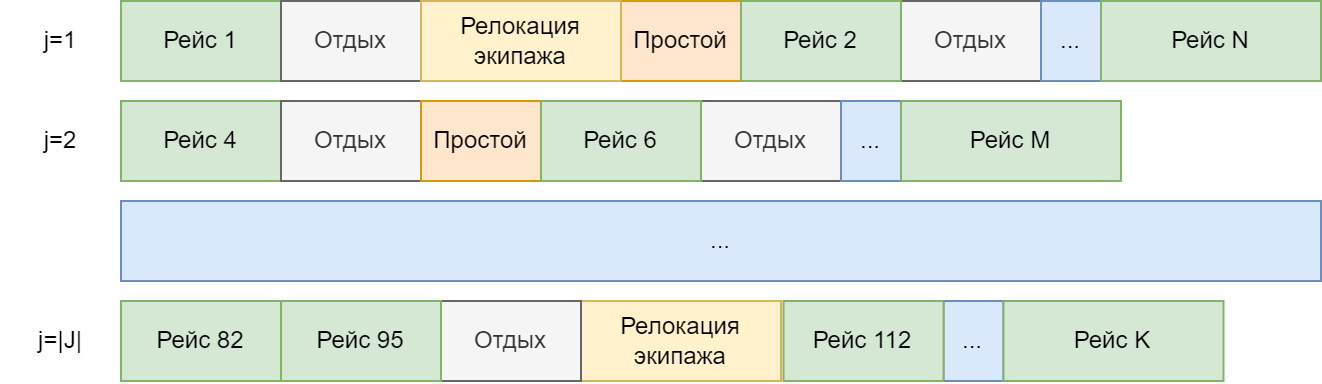
Кол-во возможных сменных графиков значительно больше кол-ва рейсов , потому что графики состоят из различных допустимых наборов рейсов.

Математическая постановка

$i \in I$ - множество запланированных рейсов;

$j \in J$ - множество допустимых сменных графиков, каждый из которых может выполнить один экипаж;

$\textbf{a}_j$ - булевый |I| -мерный вектор констант, где -ая компонента равна 1, если соответствующий рейс находится в сменном графике . В противном случае - 0. Тот самый сменный график в векторной форме;

x_j - бинарная переменная, принимает значение 1, если сменный график выбран к исполнению, в противном случае- 0;

Ограничение - покрытие каждого рейса как минимум одой сменой:

$\sum_{j \in J} a_{ij}x_j \ge 1, \quad \forall i \in I$

В целевой функции минимизируем кол-во сменных графиков для обеспечения выполнения всех запланированных рейсов (кол-во сменных графиков = кол-во экипажей):

$\min \sum_{j \in J} x_j.$

Python реализация задачи CSP

Данные для задачи CSP сгенерируем случайным образом. По умолчанию стоит маленький кейс. Чтобы получить расширенную задачу, необходимо указать is_small = False. Поиск оптимального решения полной задачи на расширенных данных займет приличное время.

Генерация входных данных.

# Импортируем необходимые библиотеки
from ortools.linear_solver import pywraplp
import pandas as pd
import numpy as np
import random
import time

# Подготовка искусственного сценария данных
is_small = True  # Переключатель размерности данных
trips_cnt = 30 if is_small else 200 # Кол-во рейсов
duties_cnt = 200 if is_small else 4000 # Кол-во сменных графиков
seed = 3

rng = np.random.default_rng(seed=seed)
df = rng.choice(100, size=(trips_cnt, duties_cnt))

columns = [f"duty_{i + 1}" for i in range(duties_cnt)]
indexes = [f"trip_{i}" for i in range(trips_cnt)]

# Вектор весов целевой функции.
c = np.array([1 for i in range(duties_cnt)])

# Инициализируем матрицу А
A = pd.DataFrame(df, columns=columns, index=indexes)
A = A / 100 - 0.3 if is_small else A / 100 - 0.48  # Прореживаем сменные графики
A = A.round().astype(int)
A = A.to_numpy()

# Проверим, что для каждого рейса есть хотя бы один сменный график, который его покрывает
sat = A.sum(axis=1)
sat[sat[0] == 0]

Задача RMP (MIP).

# Прямая MIP задача RMP
def optimize_primal_MIP(A, c, columns, selected_x_keys=None):
    """
      A - исходная матрица задачи
      с - вектор коэффициентов целевой функции
      columns - список сменных графиков
      selected_x_keys - список индексов сменных графиков J'
    """
    selected_x_keys = selected_x_keys or list(range(A.shape[1]))

    model = pywraplp.Solver.CreateSolver('SCIP')

    # Инициализация бинарных переменных выбора сменного графика:
    # принимает значение 1, если сменный график выбран к исполнению, в противном случае -0.
    x_vars = []
    for i in selected_x_keys:
        name = columns[i]
        x_vars.append(model.BoolVar(name=f"{name}"))

    # Добавляем ограничения в модель
    # Ограничение покрытия формируем исходя из доступного набора сменных графиков J'
    A_tmp = A[:, selected_x_keys]
    for i in range(len(A_tmp)):
        constr = model.Add(A_tmp[i] @ x_vars >= 1)

    # Целевая функция
    model.Minimize(c[selected_x_keys] @ x_vars)
    model_str = model.ExportModelAsLpFormat(False) # Задача в формате .lp

    # Поиск решения задачи
    model.EnableOutput()
    status = model.Solve()

    print("Найдено оптимальное решение: ", status == pywraplp.Solver.OPTIMAL)
    print('Целевая функция = %f' % model.Objective().Value())

    # Извлекаем и выводим решение задачи
    solution = {columns[selected_x_keys[i]]: var.solution_value()
                for i, var in enumerate(x_vars)
               if var.solution_value() }
    print(solution)

    # Вектор значений решающих переменных
    solution_vect = np.array([var.solution_value() for var in x_vars])
    return solution_vect, model_str

Двойственная задача к расслабленной RMP.

# Двойственная задача к расслабленной задаче RMP
def optimize_dual(A, c, indexes, selected_x_keys=None):
    """
      A - исходная матрица задачи
      с - вектор коэффициентов целевой функции
      indexes - список рейсов к выполнению
      selected_x_keys - список индексов сменных графиков J'
    """
    model = pywraplp.Solver.CreateSolver('GLOP')  # Солвер LP
    A_T = A.T

    # Инициализация вещественных переменных
    y_vars = []
    for i, name in enumerate(indexes):
        y_vars.append(model.NumVar(0, 2, name=f"{name}"))  # Remark: ограничение сверху будет пояснено далее

    # Добавляем ограничения в модель
    selected_x_keys = selected_x_keys or list(range(len(A_T)))
    for i in selected_x_keys:  # Строим ограничения только для сменных графиков из J'
        model.Add(A_T[i] @ y_vars <= c[i])

    # Целевая функция двойственной задачи
    model.Maximize(sum(y_vars))
    model_str = model.ExportModelAsLpFormat(False)  # Задача в формате .lp

    # Поиск решения задачи
    status = model.Solve()

    print("Найдено оптимальное решение: ", status == pywraplp.Solver.OPTIMAL)
    print('Целевая функция = %f' % model.Objective().Value())

    # Извлекаем и выводим решение задачи
    solution = {indexes[i]: var.solution_value()
                for i, var in enumerate(y_vars)}
    print(solution)

    # Вектор значений двойственных переменных (для расчета приведенной стоимости)
    solution_vect = np.array([var.solution_value() for var in y_vars])
    return solution_vect, model_str

Алгоритм генерации столбцов.

stop_bound = -1e-5  # Для остановки будем использовать число близкое к нулю
def column_generation_by_dual(A, c, indexes, columns):
    # indexes - dual variables
    # columns - primal variables

    # Инициализируем начальное множество J'
    selected_keys = [0]
    print("Инициализируем J': ", selected_keys, '\n')

    min_val = -1  # инициализация минимального значения приведенной стоимости
    iter_count = 0  # счетчик итераций
    # Критерии остановки алгоритма:
    # 1. В J/J' не осталось столбцов, которые уменьшают целевую функцию
    # 2. |J'| == |J|
    while min_val < stop_bound and len(selected_keys) < len(columns):
        iter_count += 1
        print('Итерация: ', iter_count)
        dual_solution, model_str = optimize_dual(A, c, indexes, selected_keys)

        reduced_cost = 1 - A.T @ dual_solution
        print("Приведенная стоимость: ", reduced_cost)

        best_key = reduced_cost.argmin()
        min_val = reduced_cost[best_key]
        if min_val < stop_bound:
            selected_keys.append(best_key)
            print('Индекс столбца с минимальной приведенной стоимостью: ', selected_keys, '\n')

    m, n = len(selected_keys), len(columns)
    print(f"Кол-во столбцов в RMP {m}/{n}. Степень сжатия задачи {round(100 * m / n, 3)}%")
    return selected_keys

Общий запуск сценария моделирования.

# Общий запуск
selected_keys = column_generation_by_dual(A, c, indexes, columns)
res, model_str = optimize_primal_MIP(A, c, columns)

В численном эксперименте рассмотрел два набора данных, обозначим их как усеченный сценарий (is_small=True) и расширенный сценарий (is_small=False). Оценку эффекта по производительности для алгоритма генерации столбцов предлагаю сделать по отношению к решению полной задачи.

Рассмотрим такие показатели, как степень сжатия модели - кол-во столбцов, достаточное для получения оптимального решения исходной задачи; выражается в виде процента "полезных" столбцов к общему кол-ву столбцов в задаче. Скорость выявления этого множества столбцов - время работы алгоритма генерации столбцов (CG). Время поиска оптимального решения задачи RMP MIP на множестве "полезных" столбцов. С целью оценки преимуществ решения задачи с помощью CG, найдем оптимальное решение для полной задачи, где весь набор столбцов подается на вход модели. Резюмируем отношением скорости нахождения оптимального решения полной задачи к времени расчета CG + время решения RMP MIP (Performance).

Усеченный кейс.

Степень сжатия задачи: 19.5% или 39 столбцов из 200;
Время работы алгоритма CG: ~0.565сек;
Время решения RMP MIP: ~0.373сек;
Время решения полной задачи MIP: ~2.9сек.
Performance: 2.9 / (0.565 + 0.373) = x3.

Расширенный кейс.

Степень сжатия задачи: 6.125% или 245 столбцов из 4000;
Время работы алгоритма CG: ~90сек;
Время решения RMP MIP: ~200сек;
Время решения полной задачи MIP: ~1160сек.
Performance: 1160 / (200 + 90) = x4.

Проблема инициализации. В нашем случае, в качестве начального множества столбцов взяли нулевой (selected_keys = [0]), но настолько бездумно поступать недопустимо при инициализации алгоритма. Необходимо сформировать такой набор столбцов, который в совокупности покрывает каждый из рейсов (строку) хотя бы один раз - чтобы RMP была решабельная (feasible). В своей реализации добавил в двойственную задачу ограничение сверху на двойственные переменные (y_vars.append(model.NumVar(0, 2, name=f"{name}"))). Это позволило избежать неограниченности (unbounded) двойственной постановки (но прямая RMP по-прежнему infeasible, что при высоких моральных ценностях недопустимо!!!). В случае, когда изначальный набор сменных графиков покрывает весь набор рейсов (RMP - feasible), такой трюк не потребуется.

Добавление группы столбцов. С количеством итераций решение двойственной задачи становится затратнее по времени, несмотря на то, что решаем LP задачу. Чтобы сократить кол-во решений двойственных задач, иногда добавляют в RMP сразу группу сменных графиков. Можно сортировать столбцы по приведенной стоимости и добавлять topN столбцов или все столбцы с отрицательной приведенной стоимостью. Но это сказывается на качестве компрессии задачи. Кроме того, можно использовать эвристики или концепцию доминирования, чтобы формировать группу из "различных" столбцов для добавления в RMP на каждой итерации CG.

Прямая расслабленная RMP. В большинстве своем солверы позволяют извлечь оптимальное решение из прямой задачи. Поэтому реализовывать и решать двойственную задачу явно не требуется. Продемонстрирую при решении следующей задачи.

Задача раскроя

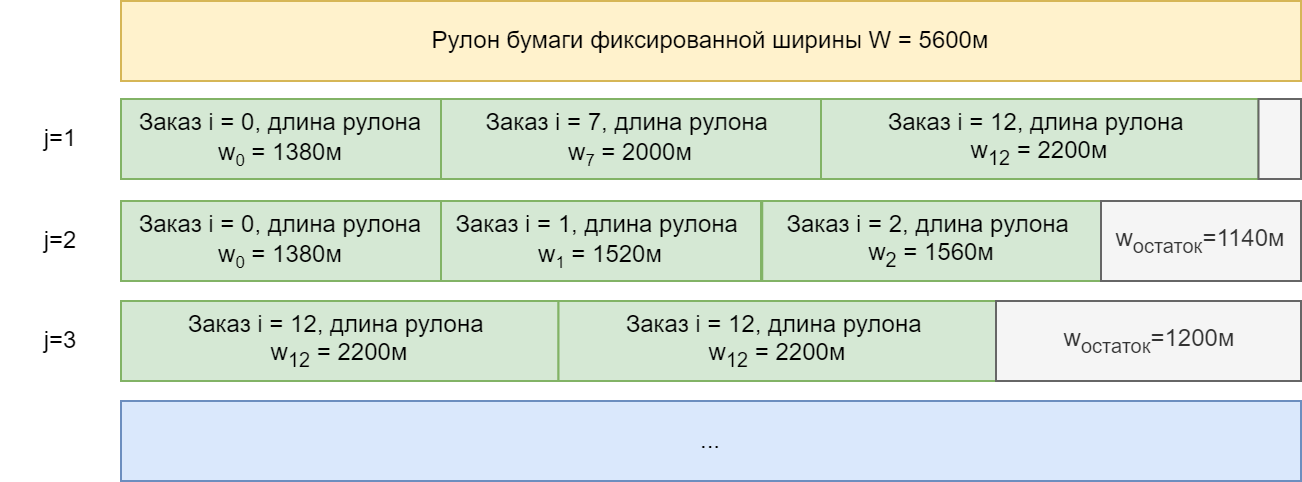
В википедии есть достаточно хорошее описание задачи, поэтому воспользуюсь уже готовым текстом.

"Представим себе, что вы работаете на целлюлозно-бумажном предприятии, и у вас имеется некоторое количество рулонов бумаги фиксированной ширины, но различным заказчикам нужны различные количества рулонов различной ширины. Как разрезать бумагу, чтобы минимизировать отходы?

Согласно данным Конфедерации европейских производителей бумаги[en][1], в 2012 году 1331 бумагоделательная машина в регионе производит в среднем отходов на 56 млн евро (примерно 73 млн долларов США) каждая. Экономии даже 1 % будет очень существенной."

Отмечу, что на хабре есть статья, посвященная задаче раскроя, которую опубликовал мой коллега. С ней можете ознакомиться здесь.

Математическая постановка

$i \in I$ - множество заказов;

$j \in J$ - множество допустимых схем раскроя, которые можно применить к фиксированной ширине производимого рулона;

$\textbf{a}_j$ - целочисленный |I| -мерный вектор констант, где -ая компонента соответствует кол-ву рулонов с шириной заказа , которое получаем при схеме раскроя ;

q_i - целочисленная константа, объем заказа . Кол-во рулонов определенной ширины, требуемых по заказу ;

x_j - целочисленная переменная, кол-во раз применения схемы раскроя ;

$\sum_{j \in J} a_{ij}x_j \ge q_i, \quad \forall i \in I$ - необходимо выполнить все заказы;

$\min \sum_{j \in J} x_j$ - минимизируем кол-во рулонов фиксированной ширины к производству.

Постановка, представленная выше, предполагает наличие всех возможных схем раскроя в явном виде. На входе известны ширина производимого рулона (фиксированная ширина производства) и ширина рулона, требуемого по заказу . Тогда допустимые схемы раскроя можно задать следующим неравенством:
$\sum_{i \in I} a_{ij} w_i \le W$ , где w_i - ширина рулона по заказу , а - ширина фиксированного рулона. Неявный вид схем раскроя можно использовать на этапе расчета приведенной стоимости (reduced cost).

Выбор схемы раскроя для добавления в RMP в явном виде:

$j_B = \text{arg} \min \{\bar{c_j} = 1-u^\intercal \textbf{a}_j|j \in J\}$ .

Теперь представим, что вектор (схему раскроя) $\textbf{a}_j$ мы можем построить по некоторому критерию, а именно, минимизируя приведенную стоимость. z_i - целочисленная переменная, которая соответствует кол-ву рулонов по заказу , тогда схема раскроя для добавления в RMP является оптимальным решением следующей задачи:

$\begin{align}\min 1-\sum_{i\in I} u_i z_i \\\sum_i w_i z_i \leqslant W & & \\z_i \in \mathbb{Z} \quad \forall i \in I & \\\end{align}$

Оптимальное решение $\bar{z}$ задачи целочисленного программирования будет тем самым столбцом $\textbf{a}_j$ для добавления в модель RMP. Отмечу, что полученная задача является задачей о рюкзаке.

Python реализация задачи раскроя

Набор входных данных для эксперимента взят из википедии. Набор небольшой, но в качестве примера пойдет.

В комментарии к предыдущей задаче указывал, что можно решать прямую задачу, а из солвера извлечь значения двойственных переменных. В этот раз так и поступим.

Инициализация входных данных.

# Импортируем необходимые библиотеки
from ortools.linear_solver import pywraplp
import pandas as pd
import numpy as np
import random
import time

# Входные данные
W = 5600  # Фиксированная ширина рулона, результат единицы производства
# Ширина рулона по заказам и их кол-во
data = [(1380, 22),
        (1520, 25),
        (1560, 12),
        (1710, 14),
        (1820, 18),
        (1880, 18),
        (1930, 20),
        (2000, 10),
        (2050, 12),
        (2100, 14),
        (2140, 16),
        (2150, 18),
        (2200, 20)]

data_df = pd.DataFrame(data, columns=['w', 'q'])
w = np.array(data_df['w'])  # Ширина рулона по каждому из заказов
q = np.array(data_df['q'])  # Кол-во рулонов по заказам

Расслабленная прямая задача RMP.

# Расслабленная задача RMP
def cutting_stock_relaxed(A, q, is_relaxed=True):
    """
      A - текущая матрица схем раскроя
      q - кол-во рулонов  по заказам
      is_relaxed - параметр переключения между LP и MIP задачами
    """
    m, n = A.shape

    if is_relaxed:
      model = pywraplp.Solver.CreateSolver('GLOP')
    else:
      model = pywraplp.Solver.CreateSolver('SCIP')  # На случай RMP MIP

    # Инициализация переменных
    x_vars = []
    for i in range(n):
        if is_relaxed:
          x_vars.append(model.NumVar(0, model.infinity(), name=f"x_{i}"))
        else:
          x_vars.append(model.IntVar(0, 100, name=f"x_{i}"))

    # Добавление ограничений в модель
    constraints = []
    for i in range(m):
        constr = model.Add(A[i] @ x_vars >= q[i])
        constraints.append(constr)

    # Целевая функция
    model.Minimize(sum(x_vars))
    model_str = model.ExportModelAsLpFormat(False)

    status = model.Solve()

    print('Значение целевой функции = %f' % model.Objective().Value())

    solution = {f"x_{i}": var.solution_value()
                for i, var in enumerate(x_vars)
               if var.solution_value() }

    print(solution)
    solution_vect = np.array([var.solution_value() for var in x_vars])
    if is_relaxed:
      dual_solution_vect = np.array([constr.dual_value() for constr in constraints])
    else: 
      dual_solution_vect = []
    return solution_vect, dual_solution_vect, model_str

Оптимизация схемы раскроя для построения столбца.

# Оптимизация схемы раскроя для добавления в модель
def pricing_problem(u, w, W):
    """
      u - вектор значений двойственных переменных
      w - ширина рулонов в зависимости от заказа
      W - ширина производимого рулона для раскроя
    """
    m = len(w)

    model = pywraplp.Solver.CreateSolver('SCIP')

    # Инициализация переменных
    z_vars = []
    for i in range(m):
        z_vars.append(model.IntVar(0, model.infinity(), name=f"z_{i}"))

    # Добавление ограничений в модель
    model.Add(w @ z_vars <= W)

    # Целевая функция
    model.Minimize(1 - u @ z_vars)

    status = model.Solve()

    print('Значение целевой функции = %f' % model.Objective().Value())

    solution = {f"z_{i}": var.solution_value()
                for i, var in enumerate(z_vars)
               if var.solution_value() }
    print(solution)
    solution_vect = np.array([var.solution_value() for var in z_vars])
    return solution_vect, model.Objective().Value()

Алгоритм генерации столбцов.

# Алгоритм генерации столбцов для задачи раскроя в случае неявного задания схем раскроя
def cutting_stock_col_gen(q, w, W):
    # Инициализация решения
    m = q.shape[0]  # кол-во ограничений
    # Инициализируем начальный набор схем: одна схема - один заказ
    A = np.eye(m, dtype=int)

    iter_count = 0
    while True:
        iter_count += 1
        print('Итерация', iter_count)

        sol, dual_sol, m_str = cutting_stock_relaxed(A, q)
        new_pattern, obj = pricing_problem(dual_sol, w, W)
        if obj >= 0:
            break
        new_pattern = new_pattern.astype(int)
        print('Новая схема: ', new_pattern)

        new_pattern_matr = new_pattern.reshape((-1, 1))
        A = np.hstack((A, new_pattern_matr))

    return A

Общий запуск сценария моделирования.

A_schemes = cutting_stock_col_gen(q, w, W)
res_vec, _, _ = cutting_stock_relaxed(A_schemes, q, is_relaxed=False)

В результате алгоритма генерации столбцов получим матрицу A_schemes, которая содержит достаточное кол-во схем раскроя, чтобы получить оптимальное решение полной задачи.

Провели самую очевидную инициализацию алгоритма: в начальный набор схем раскроя добавили схему одного разреза, когда весь произведенный рулон отдаем под один заказ. Конечно, более умная эвристика позволит сократить время генерации столбцов и ускорит процесс решения.

Показатели алгоритма:

Кол-во итераций CG: 37шт;
Время работы CG: ~1.42сек;
Время оптимизации RMP: ~0.05сек;
Оптимальное кол-во рулонов: 73шт.

Интегральная проверка решения. По заказам требуется $\sum_{i \in I} w_iq_i=407160$ м бумаги, запланировано к производству 5600*73=408800м, остаток 1640м или в среднем 1640 / 73 ~ 22.47м с рулона. Кроме этого, результат сходится с википедией.

Вы можете убедиться в достоверности полученного решения путем реализации своей версии решения задачи раскроя или эвристики инициализации алгоритма CG. Пишите в комментариях, обсудим производительность!

Финальное слово

Алгоритм генерации столбцов (Column Generation) - инструмент уменьшения размерности задачи. Сильным сигналом к применению данного метода является вытянутая матрица по кол-ву столбцов.

В статье кратко изложил математическое обоснование подхода. Схема работы алгоритма позаимствована у симплекс метода, поэтому в статье присутствует часть описания симплекс метода.

На практических примерах продемонстрировал способы применения алгоритма для явного и неявного случаев задания столбцов. Рассмотрел задачи планирования графиков смен экипажей в жд пассажира-перевозках и раскроя.

Метод генерации столбцов предоставляет широкие возможности применения эвристик: инициализация алгоритма, размер батчей столбцов для добавления в RMP, отбор столбцов не только по приведенной стоимости, но и с учетом доминирования, стабилизация алгоритма генерации столбцов и др.

Существуют более специфические модификации алгоритма, например: строко-столбцовая генерация; генерация столбцов зависимых от строк; использование на этапе branch-and-bound.

На практике мне доводилось несколько раз применять этот подход (в BIA Technologies, Huawei и ПГК). Всегда всплывали свои нюансы. Несмотря на это, кратный рост производительности алгоритмов оптимизации оправдывал использование генерации столбцов.

Ссылки

Ссылка на Jupyter Notebook;
Обзор задачи CSP;
Задача раскроя;
Обзор по алгоритму генерации столбцов;
Формализованное описание алгоритма.

См. также

Моделирование нелинейных функций - обзор.