Эта статья продолжает вводные статьи об асимптотическом анализе сложности алгоритмов на Хабре. Здесь вы узнаете о smoothed анализе и об особенностях анализа алгоритмов во внешней памяти. Любознательных ждут ссылки на дополнительный материал, а в конце я съем полином.

Что нужно знать перед началом?

По долгу службы я собеседовал студентов для программ стажировки и обучающих курсов. Ни один из тех студентов не знал четкого определения «О»-большое. Поэтому я крайне советую обратиться за таким определением к математической литературе. Базовые сведения в популярной форме вы найдете в цикле статей «Введение в анализ сложности алгоритмов»

Smoothed analysis

Скорее всего, вы впервые слышите это словосочетание. Что неудивительно, т.к. Smoothed анализ появился по меркам математики недавно: в 2001 году. Разумеется это подразумевает, что идея не лежит на поверхности. Я буду считать, что вам уже известен анализ худшего случая, анализ среднего, а так же сравнительно бесполезный анализ лучшего случая: и того три очевидных варианта. Так вот smoothed analysis — четвертый вариант.

Прежде чем объяснить зачем он понадобился, проще сперва уточнить зачем придумали предыдущие три. Я знаю три ключевых ситуации, в которых асимптотический анализ выручает:

— Во время защиты диссертации по математике.
— Когда надо понять почему один алгоритм быстрее другого или потребляет меньше памяти.
— Когда надо предсказать рост времени работы или используемой памяти алгоритма в зависимости от роста размера входа.

Последний пункт справедлив с оговорками. Из-за того, что реальное железо устроено сложно, теоретическая оценка характера роста будет работать как оценка снизу для того, что вы увидите в эксперименте. Я сознательно опускаю расшифровку слова «сложно», т.к. она займет не мало времени. Поэтому я надеюсь, что читатель понимающе кивнет и не станет меня допрашивать.

Для наших целей важно уточнить, что асимптотическая оценка не говорит какой алгоритм работает быстрее, и уж тем более ничего не говорит о конкретной реализации. Асимптотика предсказывает общий вид функции роста, но не абсолютные значения. Алгоритмы быстрого умножения — хрестоматийный пример такой ситуации: метод Карацубы обгоняет наивный только после достижения длины в «несколько десятков знаков», а метод Шёнхаге — Штрассена обгоняет метод Карацубы при длине «от 10 000 до 40 000 десятичных знаков». Невозможно сделать подобные выводы без эксперимента, если смотреть только на асимптотику.

С другой стороны имея на руках результаты эксперимента нельзя сделать вывод, что подобная тенденция будет сохраняться всегда или что нам не повезло с входными данными. В этой ситуации и выручает асимптотический анализ, который помогает доказать, почему алгоритм сортировка Хоара быстрее пузырька. Другими словами одновременно необходимы как экспериментальные данные, так и теоретические результаты для полного понимания и душевного спокойствия.

Это объясняет наличие одной асимптотической оценки, но зачем остальные? Всё просто. Допустим у двух алгоритмов асимптотическая оценка худшего случая одинакова, а результаты экспериментов говорят об явных преимуществах одного над другим. В такой ситуации придется анализировать средний случай в поисках разницы, которая всё объяснит. Именно это происходит при сравнении сортировки Хоара и пузырька, у которых асимптотически одинаковый худший случай, но разный средний.

Smoothed оценка находится посередине между средним и худшим случаем. Она записывается так:

$$

, где $$ некоторая небольшая константа, $$ множество возможных входных данных размера $$, $$ функция возвращающая время (или память), которое алгоритм затратит на обработку конкретных данных, $$ — математическое ожидание, а скобки разные для удобства.

Говоря простым языком smooth оценка означает, что не существует достаточно большого непрерывного куска данных, на которых алгоритм будет работать в среднем медленнее, чем $$. Таким образом smoothed оценка сильнее средней, но слабее худшей. Очевидно что варьируя $$ можно смещать её от среднего к максимуму.

Поскольку определение не тривиально я нарисовал картинку для понимания:

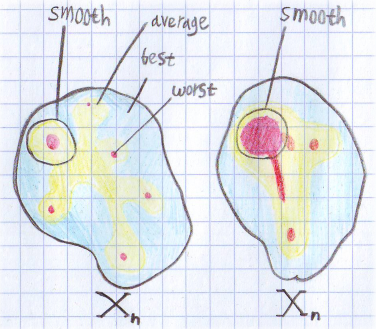Тут нарисовано распределение времени по множеству входных данных для некоторого n. Красные области — худший случай, желтые — средний, а голубые — лучший. Для левого множества средняя и smoothed оценка будут примерно одинаковыми. А вот для правого smoothed оценка будет ближе к худшему случаю. Для обоих множеств smoothed оценка точнее описывает поведение алгоритма. Если представить, что оба рисунка соответствуют одной и той же задаче, но разным алгоритмам, получается интересная ситуация. Оценка лучшего, худшего и среднего случая у них одинаковая. Но на практике левый алгоритм будет работать по ощущениям лучше, т.к. на правый намного проще устроить алгоритмическую атаку.

Подробнее об этом можно прочитать в статье «Smoothed Analysis of Algorithms». В ней применяют этот подход для анализа симплекс метода. По ссылкам можно найти и другие статьи.

Анализ алгоритмов во внешней памяти

Прежде чем говорить об алгоритмах во внешней памяти стоит подчеркнуть один момент, который обходят стороной. Теоретические оценки, о которых велась речь, формально выводятся не абы где, а в модели под названием «RAM машина». Это такая модель, в которой доступ к произвольному месту памяти происходит за одну элементарную операцию. Таким образом вы приравниваете вычислительные операции и операции с памятью, что упрощает анализ.

Внешняя память это диск, сеть или другое медленное устройство. Для анализа алгоритмов оперирующих с ними используют другую модель выполнения во внешней памяти. Если упрощать, то в этой модели у компьютера есть $$ машинных слов внутренней памяти, все операции с которой, ничего не стоят, так же ничего не стоят вычислительные операции на CPU, а ещё есть внешняя память, с которой возможно работать только целыми блоками размера $$ слов и каждая такая операция считается элементарной. Причем $$ значительно больше $$. В этой модели говорят об IO сложности алгоритма.

Таким образом даже если решать на каждом блоке NP-полную задачу в памяти, это не повлияет на IO-сложность алгоритма. Но в такой формулировке это не большая проблема поскольку блок имеет фиксированную длину и мы просто говорим, что вот такая у нас элементарная операция. Однако модель будет не применима для алгоритма драматически уменьшающего число операций на CPU ценой увеличения операций с диском, так что в итоге это будет выгодно. Но даже в таком случае, нужно что бы этот размен был нетривиальным. Причем размен в обратную сторону укладывается в модель, поэтому добавление сжатия не вызывает сложностей. А замена медленного алгоритма сжатия на более быстрый, относится к тривиальному размену.

Второе отличие от RAM модели — формат операций. Оперировать можно только крупными непрерывными блоками. Это отражает работу с дисками на практике. Которая в свою очередь обусловлена тем, что у дисков разрыв между скоростью последовательных операций по сравнению с внутренней памятью меньше, чем аналогичный разрыв между операцией с произвольной ячейкой. Таким образом выгодно нивелировать время позиционирования. В модели мы просто говорим, что нам это удалось и времени позиционирования нет, но есть непрерывные блоки длины $$, достаточной что бы модель была корректной.

При анализе в этой модели будьте аккуратны с округлением, т.к. чтение одного машинного слова и $$ машинных слов занимает одно и то же время. В общем случае чтение $$ последовательных слов занимает $$ операций, и при небольших $$ вклад округления будет значительным, особенно если потом эта величина умножается на что-то.

Из-за особенностей модели задачи начинают решаться будто быстрее, т.к. вычислительные операции ничего не стоят. Например сортировка слиянием выполняется за $$, что намного быстрее чем могло бы быть. Но не стоит обманываться, при фиксированных $$ и $$, все это дает лишь мультипликативную константу, которую легко съедает диск.

SSD и кэш

Есть две темы, которые нельзя обойти. Начнем с кэша. Логика примерно следующая: в целом отношения кэша и оперативной памяти похожи на отношения памяти и диска. Но есть один нюанс: у оперативной памяти нет лага на случайный доступ. Несмотря на то, что чтение из L1 кэша примерно в 200 раз быстрее, чем чтение из памяти, все таки основа модели в лаге на поиск. Существует альтернативная постановка вопроса: составить алгоритм так, что бы минимизировать число промахов кэша, но это тема для отдельного разговора.

SSD всего в 4 раз медленнее памяти на последовательное чтение, но в 1500 раз медленнее на случайное чтение. Именно по этому модель в целом справедлива для него, т.к. вы все равно будете хотеть нивелировать лаг на поиск.

Таким образом эта модель хоть и простая, но остается корректной в большом числе случаев. Подробнее об алгоритмах во внешней памяти с примерами анализа предлагаю ознакомиться в курсе Максима Бабенко из 5 лекций.

Бонус

Напоследок расскажу об интересном обозначении, применяемом при анализе NP-полных задач. Сам я узнал о таком обозначении в лекциях Александра Куликова «Алгоритмы для NP-трудных задач».

Неформально символ «О»-большое съедает всё кроме старшего члена, а у старшего члена съедает мультипликативную константу. Оказывается, существует символ $$, который съедает не просто мультипликативную константу, а целый полином. Т.е. $$, и $$. Так что если вам станет грустно из-за того, что ваша программа тормозит, можете утешать себя мыслью, что алгоритмически её IO-сложность $$.