Структура публикации
- Получение кватерниона из вектора и величины угла разворота
- Обратный кватернион
- Умножение кватернионов
- Поворот вектора
- Рысканье, тангаж, крен
- Серия поворотов
Получение кватерниона из вектора и величины угла разворота
Ещё раз – что такое кватернион? Для разработчика – это прежде всего инструмент, описывающий действие – поворот вокруг оси на заданный угол:
(w, vx, vy, vz),
где v – ось, выраженная вектором;
w – компонента, описывающая поворот (косинус половины угла).
Положительное значение угла разворота означает поворот вдоль вектора по часовой стрелке, если смотреть с конца вектора в его начало.
Например, кватернион поворота вдоль оси Х на 90 градусов имеет следующие значения своих компонент: w = 0,7071; x = 0,7071; y = 0; z = 0. Левая или правая система координат, разницы нет – главное, чтобы все операции выполнялись в одинаковых системах координат, или все в левых или все в правых.
С помощью следующего кода (под рукой был Visual Basic), мы можем получить кватернион из вектора и угла разворота вокруг него:
Public Function create_quat(rotate_vector As TVector, rotate_angle As Double) As TQuat
rotate_vector = normal(rotate_vector)
create_quat.w = Cos(rotate_angle / 2)
create_quat.x = rotate_vector.x * Sin(rotate_angle / 2)
create_quat.y = rotate_vector.y * Sin(rotate_angle / 2)
create_quat.z = rotate_vector.z * Sin(rotate_angle / 2)
End Function
В коде rotate_vector – это вектор, описывающий ось разворота, а rotate_angle – это угол разворота в радианах. Вектор должен быть нормализован. То есть его длина должа быть равна 1.
Public Function normal(v As TVector) As TVector
Dim length As Double
length = (v.x ^ 2 + v.y ^ 2 + v.z ^ 2) ^ 0.5
normal.x = v.x / length
normal.y = v.y / length
normal.z = v.z / length
End Function
Не забывайте про ситуацию, когда длина может быть 0. Вместо ошибки вам может понадобиться обработать эту ситуацию индивидуально.
Обратный кватернион
Для поворота вектора кватернионом требуется уметь делать обратный разворот и правильно выполнять операцию умножения кватернионов. Под обратным разворотом я имею ввиду обратный кватернион, т. е. тот, который вращает в обратную сторону.
Чтобы получить обратный кватернион от заданного, достаточно развернуть вектор оси в другую сторону и при необходимости нормализовать кватернион. Нормализация кватерниона так же как и в векторах, это просто приведение к длине = 1.
Public Function quat_scale(q As TQuat, val As Double) As TQuat
q.w = q.w * val ' x
q.x = q.x * val ' x
q.y = q.y * val ' y
q.z = q.z * val ' z
quat_scale = q
End Function
Public Function quat_length(q As TQuat) As Double
quat_length = (q.w * q.w + q.x * q.x + q.y * q.y + q.z * q.z) ^ 0.5
End Function
Public Function quat_normalize(q As TQuat) As TQuat
Dim n As Double
n = quat_length(q)
quat_normalize = quat_scale(q, 1 / n)
End Function
Public Function quat_invert(q As TQuat) As TQuat
Dim res As TQuat
res.w = q.w
res.x = -q.x
res.y = -q.y
res.z = -q.z
quat_invert = quat_normalize(res)
End Function
Например, если разворот вокруг оси Y на 90 градусов = (w=0,707; x = 0; y = 0,707; z=0), то обратный = (w=0,707; x = 0; y = -0,707; z=0). Казалось бы, можно инвертировать только компоненту W, но при поворотах на 180 градусов она = 0. Кватернион, который означает «нет разворота» = (w=1; x = 0; y = 0; z=0), то есть у него длина вектора оси = 0.
Умножение кватернионов
Умножение кватернионов крайне полезная штука. Результатом умножения является кватернион, который после поворота даёт такой же результат, если последовательно выполнить развороты умножаемыми кватернионами. Причём разворот будет происходить в локальной для поворачиваемого вектора системе отчёта, т. е. система отчёта поворачиваемого вектора также двигается.


Умножение кватернионов выполняется следующим образом:
Public Function quat_mul_quat(a As TQuat, b As TQuat) As TQuat
Dim res As TQuat
res.w = a.w * b.w - a.x * b.x - a.y * b.y - a.z * b.z
res.x = a.w * b.x + a.x * b.w + a.y * b.z - a.z * b.y
res.y = a.w * b.y - a.x * b.z + a.y * b.w + a.z * b.x
res.z = a.w * b.z + a.x * b.y - a.y * b.x + a.z * b.w
quat_mul_quat = res
End Function
Для того, чтобы умножить кватернион на 3D вектор, нужно вектор преобразовать в кватернион присвоив компоненте W = 0 и умножить кватернион на кватернион. Или подставить ноль и выразить это в виде функции:
Public Function quat_mul_vector(a As TQuat, b As TVector) As TQuat
Dim res As TQuat
res.w = -a.x * b.x - a.y * b.y - a.z * b.z
res.x = a.w * b.x + a.y * b.z - a.z * b.y
res.y = a.w * b.y - a.x * b.z + a.z * b.x
res.z = a.w * b.z + a.x * b.y - a.y * b.x
quat_mul_vector = res
End Function
Поворот вектора
Теперь, собственно, поворот вектора кватернионом:
Public Function quat_transform_vector(q As TQuat, v As TVector) As TVector
Dim t As TQuat
t = quat_mul_vector(q, v)
t = quat_mul_quat(t, quat_invert(q))
quat_transform_vector.x = t.x
quat_transform_vector.y = t.y
quat_transform_vector.z = t.z
End Function
Пример:
Вектор описывающий ось (x=1; y=0; z=1). Угол поворота 180 градусов.
Поворачиваемый вектор (x=0; y=0; z=1). Результат равен (x=1; y=0; z=0).

Рысканье, тангаж, крен
Рассмотрим инструмент формирования кватерниона с помощью поворотов вокруг одной из осей:
Рысканье = heading = yaw = вокруг оси Z; тангаж = altitude = pitch = вокруг оси Y; крен = bank = roll = вокруг оси X.
Public Function quat_from_angles_rad(angles As TKrylov) As TQuat
Dim c1 As Double
Dim c2 As Double
Dim c3 As Double
Dim s1 As Double
Dim s2 As Double
Dim s3 As Double
c1 = Cos(angles.heading / 2)
c2 = Cos(angles.altitude / 2)
c3 = Cos(angles.bank / 2)
s1 = Sin(angles.heading / 2)
s2 = Sin(angles.altitude / 2)
s3 = Sin(angles.bank / 2)
quat_from_angles_rad.x = c1 * c2 * s3 - s1 * s2 * c3
quat_from_angles_rad.y = c1 * s2 * c3 + s1 * c2 * s3
quat_from_angles_rad.z = s1 * c2 * c3 - c1 * s2 * s3
quat_from_angles_rad.w = c1 * c2 * c3 + s1 * s2 * s3
End Function
И в обратную сторону, из кватерниона:
k.bank = atan2(2 * (w * x + y * z), 1 - 2 * (sqx + sqy))
k.altitude = Application.WorksheetFunction.Asin(2 * (w * y - x * z))
k.heading = atan2(2 * (w * z + x * y), 1 - 2 * (sqy + sqz))
Серия поворотов
Рассмотрим пример:
1. Первый поворот – рысканье (вокруг Z) 90 градусов по часовой;
2. Второй поворот – тангаж (вокруг Y) 90 градусов по часовой;
3. Третий поворот – крен (вокруг X) 90 градусов по часовой.
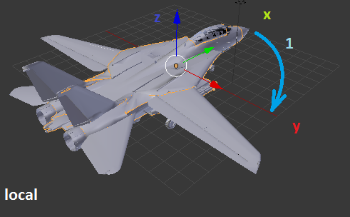
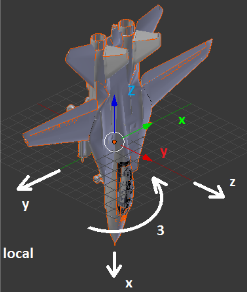
Рисунки, изображающие поворот и подписанные как «global» демонстрируют повороты относительно неподвижных осей XYZ. Такой результат мы получим, если будем использовать кватернионы разворота по отдельности. Четвёртый рисунок демонстрирует, где окажется вектор, если начальные координаты у него были X=1; Y=0; Z=0.
Рисунки, подписанные как «local» демонстрируют вращение осей вместе с самолетом. То есть все вращения происходят относительно пилота, а не относительно неподвижной системы координат. Четвёртый рисунок показывает, где окажется тот же самый вектор (1; 0; 0) в итоге всех трёх поворотов. Такой результат мы получим, перемножив кватернионы разворота и применив полученный кватернион.






Комментарии (20)

haqreu
06.04.2015 13:56+2Очень неполная статья, вообще не затронуты темы
— двойного покрытия пространства вращений единичными кватернионами
— того, что одному кватерниону соответствуют два набора углов Эйлера (ничего общего с первым пунктом)
— складывания рамок для углов Эйлера
Соответствующая статья в википедии полнее и доступнее.
1div0 Автор
07.04.2015 10:15Спасибо за замечание. Не хотел загромождать статью теоретическими деталями.
Про то, что одно и то же вращение можно описать двумя кватернионами, вроде бы и так понятно.
Например давайте опишем движение стрелки часов, если ось стрелки совпадает с осью X.


В первом кватернионе вектор оси будет направлен от лицевой стороны циферблата (w = 0,7071; x = 0,7071; y = 0; z = 0), а разворот будет осуществляться по часовой стрелке. Во втором кватернионе вектор оси и направление поворота осуществляются в обратную сторону.
Про наборы углов Эйлера и складывание рамок — это скорее для статьи про углы Эйлера-Крылова. Про наборы углов может быть интересной деталью — приведите пожалуйста пример. Если я правильно понимаю, речь о том. что например, только тангаж 90 равен курс 180, тангаж 90, крен 180.

EndUser
06.04.2015 14:36А зачем нужен Gimbals lock в статье про кватернионы? Это матричная проблема, причём матрицы вообще не тема статьи.
У меня другой вопрос к автору. Как вы вычисляете Cx и Cy?
1div0 Автор
07.04.2015 09:42Спасибо. Действительно статья о кватернионах не предполагает освещение вопроса о складывании рамок.
Должен спросить — что Вы понимаете под Cx и Cy?
EndUser
07.04.2015 11:47Скриншот с F-14D Tomcat в блендере ваш собственный — в гугле дублей нет.
Подумал, что вы делаете что-то об аэродинамике.
Подумал, что вы имеете подход к этому вопросу.
Если нет, то извините.

haqreu
07.04.2015 11:22В матрицах нет складывания рамок, это проблема рамок, которые вполне себе упоминаются — тангаж, крен и тп.

dtestyk
07.04.2015 12:01Можно ли говорить, повороты в глобальной неподвижной системе(global) координат — одновременные, а локальной(local) — последовательные? Если да, то можно ли повернуть вектор в неподвижной системе последовательно чередуя повороты на бесконечно малые углы в локальной?



mayorovp
Зачем после инверсии кватерниона делать его нормализацию?
1div0 Автор
Обратный кватернион предполагает только обратный разворот без масштабирования, поэтому нормализуется.
То есть если все компоненты кватерниона умножить на число, например на 3, то после поворота вектора таким кватернионом, длина вектора увеличится в 3 раза.
Давайте рассмотрим прикладную сторону вопроса и посмотрим на исходники от NVIDIA. Вот эта функция только отражает кватернион:
А эта функция отражает и нормализует:
Где функция нормализации выглядит так:
mayorovp
Вы приводили функцию, создающую кватернион поворота — длина этого кватерниона всегда равна 1. Обратный кватернион для него можно найти без нормализации.
Откуда вообще взялись кватернионы масштабирования? В статье про них — ни слова.
1div0 Автор
Вы правы. В рамках данной статьи длина кватерниона не меняется и в принципе можно без нормализации.
HomoLuden
В одной из публикаций на тему БИНС встречал также нормализацию кватерниона в месте, где вроде бы она не требуется. Автор специально уточнил, что в кватернионной арифметике с плавающей точкой, как и везде, могут иметь место вычислительные ошибки. Уже по этой причине в ключевых местах может иметь смысл нормализацию проводить.
mayorovp
Смена знака — эта не та операция, на которой могут накопиться погрешности.
HomoLuden
Кватернион поворота всегда должен иметь длину равную единице, но в сложных алгоритмах наподобие БИНС это требование нарушиться может. Если функция вычисления обратного кватерниона общая и неизвестно заранее, что ее не доведется использовать без предварительной нормализации, то автор мог уже хотя бы для надежности добавить нормализацию. Когда отлаживаешь алгоритм, это может быть важным.
Но в контексте статьи выглядит как излишняя предосторожность.