Градиентный спуск лежит в основе большинства методов AI/ML. Звучит как-то странно и пугающе. Спуск? Блин, надеюсь, мне не придется прыгать с парашютом...????

Не волнуйтесь, возможно, все же придется прыгнуть, но только если вы этого захотите. Это объяснение способен понять даже ваш 10-летний племянник.

Представим, что вы пытаетесь освоить новый скилл. Допустим, вы живёте в древнем племени, и ваша задача - определять вес людей по их росту. Весов еще не изобрели. Знаю, звучит нелепо, но для простоты предположим, что от этого зависит выживание племени. Итак, приходит один из ваших соплеменников и называет свой рост, а вы, опираясь на опыт, должны определить его вес, условно, в мешках с картошкой.

Так вот, ваш соплеменник Андрей говорит - мой рост - 174 сантиметра. Отметим, что вам не очень нравится Андрей, поэтому вы говорите ему что он весит 100500 мешков картошки, и он убегает в слезах... ???? Но на самом деле, по своему опыту, вы уверены, что этот парень, скорее всего, весит около 70 килограммов, или 7 мешков картошки (по 10 килограммов каждый).

Откуда вы это знаете? Ну, вы встречали немало людей с таким же ростом и типом фигуры, как у Андрея, так что вы полагаете, что это должно быть примерно так. То есть, у вас уже есть опыт.

Теперь мы хотим обучить систему, которая сможет это делать. Для этого нам нужно смоделировать предварительный опыт встречи с людьми разного роста и узнать их вес. Мы делаем это при помощи обучающих данных, которые выглядят следующим образом:

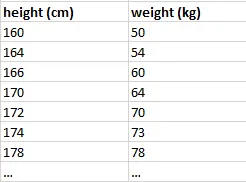
Это средняя корреляция между ростом и весом, о которой знаем точно.

Если мы построим график этих данных, то он будет выглядеть вот так:

Здесь явно прослеживается закономерность. Чем выше рост - тем больше вес. Хорошо, давайте попробуем нарисовать линию, отражающую эту закономерность. Используя эту линию, мы можем оценить вес для любого заданного роста:

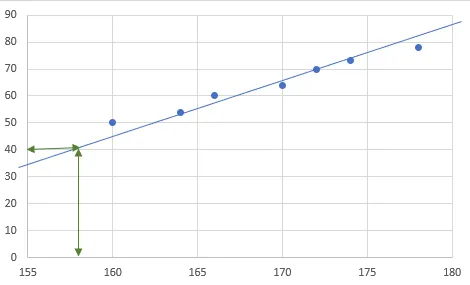
Например, для человека с ростом около 157 вес составляет около 40 килограммов. Функция, которая представляет эту линию, - это, по сути, наша AI модель. Звучит подозрительно просто, правда? Так оно и есть.????

Вся сложность возникает из-за сложных зависимостей. Зависимость "вес-рост" проста и может быть представлена простой функцией. Но в реальном мире многие зависимости (или паттерны) очень сложны и представляются весьма сложными функциями. Но давайте пока остановимся на нашей.

Линейная функция, подобная нашей, представлена следующим уравнением:

f(x) = a * x + b

or

y = a * x + b

Где: a - наклон, а b - точка пересечения с осью y. Еще больше определений ????. Но они очень просты:

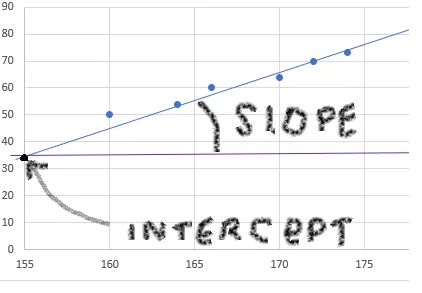
Точка пересечения (intercept) - это точка, в которой линия пересекает ось y, а наклон - угол между линией и осью x. Из простой геометрии 7го класса мы знаем, что угол треугольника здесь равен A/B (или dy/dx), как показано ниже:

Эти два параметра, a и b, являются коэффициентами или параметрами нашей модели. В больших моделях, таких как OpenAI, существуют миллиарды параметров и базовая функция отличается, но принцип тот же.

Итак, перейдем к процессу обучения. Мы решили, что в нашем случае будем использовать простую линию для представления корреляции между ростом и весом. То есть функция линейная. Именно поэтому ее также называют линейной регрессией. Часть названия "регрессия" является исторической, я объясню это в конце.

Как нам найти правильные наклон и пересечение? Мы будем делать это так же, как осваиваем любой навык. Мы начинаем со случайной догадки, наблюдаем за результатом и корректируем догадку, если она слишком далека от истины. Это похоже на игру "холодно-горячо". Итак, мы размещаем нашу линию в случайном месте, вот так:

Мы измеряем расстояния от линии до всех наших точек, сумма этих расстояний и есть общая погрешность текущего положения линии. Она называется loss (ошибка). Наша цель - минимизировать loss, то есть расположить линию (to fit the curve) таким образом, чтобы сумма расстояний была как можно ближе к нулю. В идеале расстояние равно нулю, то есть все точки лежат на линии - но в нашем случае с нашей линейной функцией это неосуществимо. Но мы хотим, чтобы оно было как можно меньше.

Теперь мы формализовали нашу задачу обучения - мы хотим найти такие коэффициенты a и b, чтобы ошибка (loss) была как можно меньше, или, другими словами:

f(x) = a * x + b
sum ( distances_to_line (a, b) ) -> 0

Формула для расстояния D между двумя точками такова:

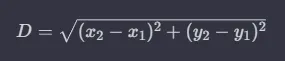
Выберем случайным образом a = 0,3125 и b =14,375.

С учётом этого выберем точку из наших обучающих данных, скажем {174 см, 70 кг}. Рассчитаем эту же точку, подставив x = 174, по нашей функции y = x *a + b, при этом a и b мы выбрали случайно выше:

y = 174 * 0,3125 + 14,375 = 40. Значит, рассчитанная точка = {174 см, 40 кг}.

Расстояние равно D = sqrt((174-174)² + (70-40)²) = 30. Значит, мы ошиблись на 30 кг. Не самая лучшая модель, нужно найти более подходящие a и b.

В приведенной выше формуле квадратный корень как таковой не нужен. Если подумать, мы используем расстояние, чтобы оценить ошибку. Мы можем легко использовать просто:

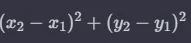
или

(расчетное значение - прогнозируемое значение)²,

где расчетное значение вычисляется с помощью нашей функции, а ожидаемое берется из обучающего набора. Меньше вычислений, а работает так же эффективно. Именно это обычно и используется, этот метод называется методом наименьших квадратов.

Если мы возьмём все точки по очереди и просуммируем расстояния, то получим общую ошибку. Теперь мы немного изменим a и b и снова рассчитаем ошибку. Если выходит меньше, чем раньше - значит, мы движемся в правильном направлении. Когда мы перестанем менять коэффициенты, то есть как мы узнаем, что найденные нами a и b достаточно хороши? Ну, это решение остается за нами, но я бы сказал, что если ошибка для каждой точки мала - это достаточно хорошо. То есть если наша модель угадывает 70,2 кг для роста 174 см, то это очень близко к 70 кг. Если ошибка так мала для каждой точки - нам не обязательно улучшать модель дальше.

Таким образом, если:

total error = (sum of errors/number of points) ≤ 0.2

мы прекращаем обучение.

Теперь нам осталось найти способ передвигать линию функции, изменяя a и b, в направлении, которое минимизирует суммарную ошибку! Если мы будем менять их случайным образом, это займет слишком много времени. Наконец, мы подошли к градиентному спуску. Такой длинный путь!

Градиентный спуск

Градиентный спуск - это метод поиска минимума функции. Это как раз то, что нам нужно. Как удобно! ????

В нашем случае общая ошибка - total error, которую мы хотим минимизировать, является функцией от a и b, то есть:

total_error = f(a, b) = sum(distances_to_line (a, b)) =
distance({x1, y1_train} , {x1, y1}) +
distance({x2, y2_train} , {x2, y2}) +
…
+ distance({xn, yn_train} , {xn, yn})

Если мы попробуем еще несколько случайных значений a и пока оставим b постоянным, то увидим, что функция total error выглядит следующим образом:

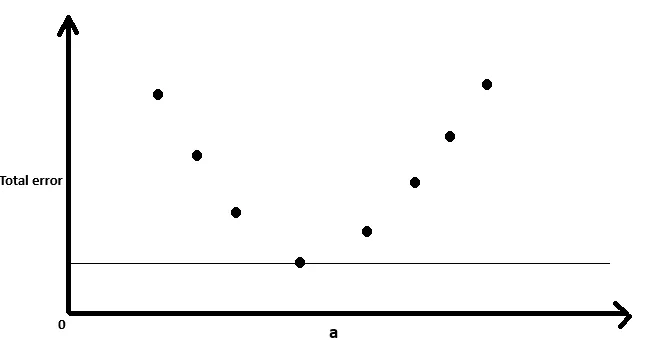
При определенных значениях a суммарная ошибка меньше. Градиент - это склон, как в долине, и поскольку нам нужен минимум, мы должны двигаться вниз по склону. Другими словами, нам нужно спуститься. Мы находимся в какой-то случайной точке, которую выбрали в начале, а искомый минимум - это сокровище на дне долины, и чтобы его найти, нам нужно спуститься вниз.

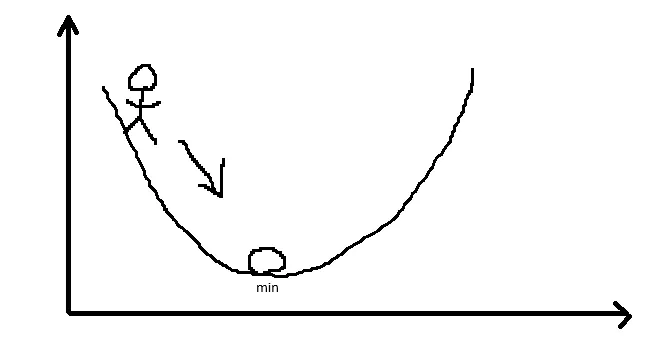
Дело в том, что на самом деле мы не знаем, где находится сокровище в начале - иначе мы бы просто выбрали эту точку, а не случайную????. Так что это выглядит примерно так:

Мы знаем, что находимся где-то на склоне, знаем, что сокровища где-то внизу, но не знаем, где это дно. Что мы знаем - нам нужно спуститься вниз и по пути осмотреться в поисках сокровищ. Поэтому мы медленно спускаемся и смотрим. В этом и заключается суть градиентного спуска.

Работает это так: мы берем производную функции ошибки в нашей случайной точке. Производная - это наклон касательной к линии функции в этой точке, или, проще говоря, она указывает на направление увеличения/уменьшения наклона, а ее значение говорит нам, насколько крут наклон. В минимуме производная равна нулю, потому что это минимум, а значит, уклона нет (как на дне долины - земля ровная):

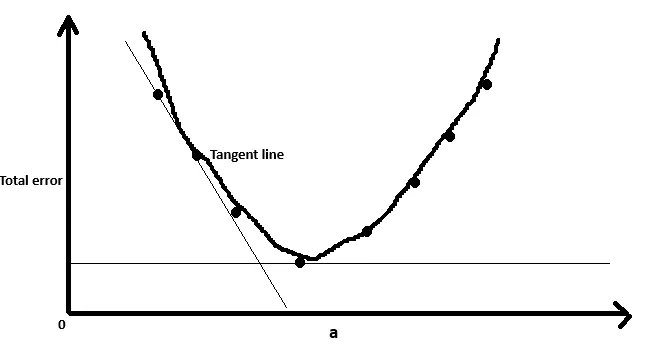
Поэтому нам нужно двигаться в направлении уменьшения наклона. Мы добавляем производную, умноженную на размер шага (называемый скоростью обучения, learn rate), к нашему коэффициенту и вычисляем новую общую ошибку, и повторяем этот процесс до тех пор, пока наша общая ошибка не станет меньше 0,2. Скорость обучения - это произвольное число, которое подбирается методом проб и ошибок, но обычно оно достаточно мало, чтобы мы не прыгали слишком быстро, иначе может произойти вот это:

Это и есть процесс градиентного спуска:

1. берем производную от функции ошибки

2. умножаем ее на скорость обучения

3. и добавляем результат к параметру, который мы пытаемся оптимизировать

4. используем обновленный параметр для расчета новой ошибки

5. если нужный порог точности не достигнут - повторяем процесс

Я не буду рассказывать о том, как вычислить производную, - это базовая школьная формула, и она не так важна, если вы понимаете, что такое производная. Производная показывает, как изменяется наклон и в каком направлении:

1. Скорость изменения: С геометрической точки зрения производная показывает, насколько крут график в любой точке. Большое абсолютное значение производной указывает на крутой наклон (быстрый рост или падение), а малое абсолютное значение указывает на малый наклон (плавный рост или падение).

2. Положительный или отрицательный наклон: Если производная в точке положительна, то функция возрастает в этой точке, то есть наклон касательной линии направлен вверх. И наоборот, если производная отрицательна, функция убывает, а наклон касательной линии направлен вниз.

3. Нулевая производная: Когда производная в точке равна нулю, это означает, что наклон касательной линии горизонтален. Такие точки являются локальными максимумами, локальными минимумами или точками перегиба функции.

Примечания к особенностям градиентного спуска

Следует отметить, что градиентный спуск не гарантирует нахождения глобального минимума. Он может найти локальный минимум и остановиться на нем, если выполняются пороговые условия. Это зависит от таких факторов, как форма функции, первоначально выбранные случайные параметры, скорость обучения и так далее…

Историческая справка о регрессии

Как я и обещал, вот исторические корни слова "регрессия" в "линейной регрессии" имеет историческое происхождение. Впервые его использовал сэр Фрэнсис Гальтон, английский исследователь, в контексте своих исследований наследственности. В конце XIX века Гальтон изучал взаимосвязь между ростом родителей и их детей. Он наблюдал явление, которое назвал "регрессией к посредственности" (сейчас это чаще называют "регрессией к среднему").

Гальтон заметил, что, хотя у высоких родителей, как правило, рождались дети выше среднего роста, эти дети, как правило, не были такими же высокими, как их родители. Аналогично, дети низкорослых родителей, как правило, были ниже среднего роста, но не такими короткими, как их родители. Другими словами, рост детей имел тенденцию к "регрессии" или движению к среднему показателю роста населения.

Позднее работа Гальтона была математически формализована Карлом Пирсоном и другими учеными, которые разработали метод наименьших квадратов для нахождения наилучшей линии, проходящей через набор точек данных. Этот метод использовался для количественной оценки силы и характера взаимосвязи между двумя переменными, и этот процесс они назвали "регрессионным анализом".

Со временем термин "регрессия" стал ассоциироваться со статистическими методами, используемыми для моделирования и анализа взаимосвязи между переменными.

Пример внедрения линейной регрессии можно посмотреть тут :https://colab.research.google.com/drive/1PkuGT8sK6CLYz5_CheUa21aMSBKCySKY?usp=sharing