Вступление
Метод быстрого марша (Fast Marching Method) был разработан Джеймсом Сетианом для решения краевых задач уравнения Эйконала.
Мы будем использовать этот алгоритм для расчёта полей расстояний (Distance Field) и поиска кратчайшего пути. Задача этой статьи - объяснить принцип работы алгоритма и показать примерную реализацию. Для дальнейшего чтения, в конце статьи приведены ссылки на источники.
Математическое описание FMM
Обычно в статьях описывают этот метод как "масляное пятно" растекающееся по поверхности. На рисунке показан пример распространения волны от точки в центре.
Масло растекается по поверхности с разной скоростью, которая зависит от функции скорости .Предполагается, что
всюду кроме исходной точки. Если это не так, то данный алгоритм использовать нельзя. Если скорость постоянна, то уравнение Эйконала удовлетворяет функции расстояний. Для поиска расстояния мы будем рассчитывать время
прибытия в точку. Мы будем использовать FMM для двухмерного случая, но метод можно использовать и для пространств больших размерностей.
Градиент(изменение времени) рассчитывается как евклидова норма:
Для применения алгоритма, мы должны преобразовать изображение в набор узлов, где каждый пиксель это узел. Мы будем вычислять используя значения соседних узлов. Будем брать узел справа, слева, сверху и снизу. Для простоты, узлы имеют названия частей света.
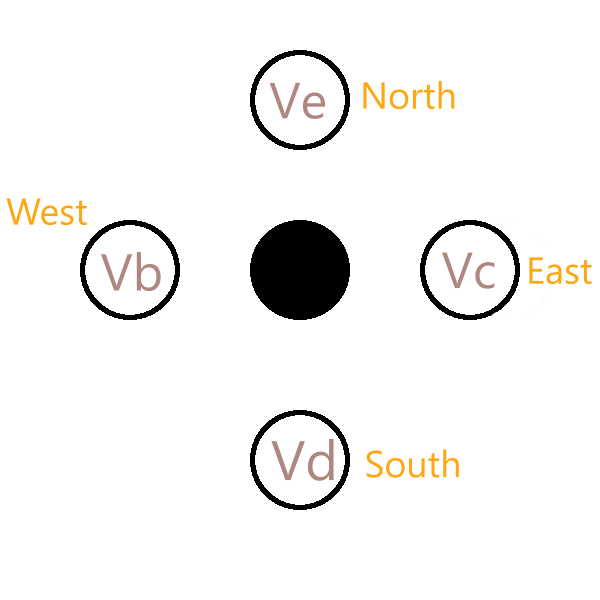
Значение рассматриваемого узла задаётся уравнением:
Очевидно, что мы должны использовать самое маленькое значение из двух:
Распишем уравнение, заменяя условные обозначения:
Задача сводится к решению квадратного уравнения, где - значение рассчитываемого узла. Для решения мы будем использовать метод предложенный в работе R. Kimmel and J.A. Sethian (1996):
Мы будем рассчитывать значения для каждого узла, выбирая сначала ближайшие. Алгоритм выполняется итерационно пока не пройдёт все узлы.

Описание реализации FMM
Для начала нам нужно получить набор узлов для расчёта полей расстояний. Можно сгенерировать их, а можно взять изображение и конвертировать его в набор узлов.
Вот пример структуры Node. Весь код приведён на C#.
public enum StateNode
{
KNOWN,
NEIGHBOUR,
FAR,
BLOCK,
WAY
}
public struct Node
{
public int x;
public int y;
public StateNode state;
public double distance;
}KNOWN мы будем помечать уже известные узлы,
NEIGHBOUR - соседи уже известных узлов,
FAR - не посещённые узлы,
BLOCK - препятствие(узел, который не может использоваться как путь),
WAY - узел пути(понадобится для рисования кратчайшего пути из точки А до Б, но необязателен для создания карты расстояний).
Сам Node имеет координаты x, y, состояние и собственно значение distance. Можно также сохранять в узлах значение цвета пикселя, для восстановления исходного изображения.
Узлы будем помещать в
List<List<Node>> nodes = new List<List<Node>>();Такая структура данных поможет проще обращаться к соседним узлам. Например:
int x = node.x;
int y = node.y + 1;
Node node_neighbour = nodes[x - 1][y - 1]; // сосед сверхуПолучить списки узлов можно разными способами и это не так важно, поэтому сначала я опишу реализацию самого алгоритма, а в конце статьи покажу пример преобразования изображения.
Так же нам нужно будет постоянно находить ближайшие узлы с наименьшим значением DISTANCE. Для этого будем использовать "двоичную кучу." Реализовать кучу можно любым способом, главное, чтобы мы могли легко добавлять туда узлы и доставать от туда узел с наименьшим значением DISTANCE.
// взять наименьшее значение neighbour
Node min_neighbour = binaryHeapNodeClass.getMinimum();
// добавление узла в кучу
binaryHeapNodeClass.add(node);
// получение количества узлов в куче
binaryHeapNodeClass.heapSize;
// перестройка дерева после удаления узла в основании.
binaryHeapNodeClass.heapify(0);Сам алгоритм
Перед началом основного цикла, мы должны добавить первые узлы в двоичную кучу. Первыми neighbours будут уже известные узлы, которые являются входными данными:
private void AddKnowNodeFromImage()
{
for(int i = 0; i < nodes.Count; i++) // immage height
{
for(int j = 0; j < nodes[0].Count; j++) // image width
{
if (nodes[i][j].state == StateNode.KNOWN) // проверяем, что это нужный узел
{
Node node_know = nodes[i][j];
node_know.distance = 0;
node_know.state = StateNode.NEIGHBOUR;
nodes[i][j] = node_know;
binaryHeapNodeClass.add(node_know); // добавляем узлы в кучу
}
}
}
}Алгоритм:
Если двоичная куча не пуста, то начать алгоритм. Если пуста - закончить алгоритм.
Взять neighbour с наименьшим distance из кучи и удалить его из кучи.
Вычислить значения расстояний для соседей этого узла.
Переместить соседей этого узла в кучу. Сам этот узел пометить как KNOW и обновить его значение в общем списке узлов.
Перейти к шагу 1.
while(binaryHeapNodeClass.heapSize > 0)
{
// взять наименьшее значение neighbour(узел автоматически удаляется из кучи)
Node min_neighbour = binaryHeapNodeClass.getMinimum();
binaryHeapNodeClass.heapify(0);
// вычислить значение соседей
// переместить соседей в neighbours
CalculateNeighboursThisNode(min_neighbour);
// пометить узел как KNOW
min_neighbour.state = StateNode.KNOWN;
nodes[min_neighbour.x - 1][min_neigh.y - 1] = min_neighbour;
// повторить
}Мы берём соседей сверху, справа, снизу и слева, и добавляем их в кучу . Если узел вышел за границы сетки, то ничего не возвращаем.
private void CalculateNeighboursThisNode(Node node)
{
TryNeighbourNode(node.x, node.y + 1);
TryNeighbourNode(node.x, node.y - 1);
TryNeighbourNode(node.x - 1, node.y);
TryNeighbourNode(node.x + 1, node.y);
}
private void TryNeighbourNode(int x, int y)
{
try
{
Node node = nodes[x - 1][y - 1];
if (node.state == StateNode.FAR) // Проверяем, что узел не посещённый
{
Node node_neighbour = node;
node_neighbour.state = StateNode.NEIGHBOUR;
//расчитываем значение расстояния для это узла
node_neighbour = CalculateDistanceThisNode(node_neighbour);
nodes[x - 1][y-1] = node_neighbour;
binaryHeapNodeClass.add(node_neighbour); // добавляем в кучу
}
}
catch (ArgumentOutOfRangeException)
{
// Если узла не существует, то ничего не возвращаем
}
}Далее приводится пример расчёта расстояния для конкретного узла. Если мы вышли за границы списка, то возвращаем узел с максимальным значением.
private Node CalculateDistanceThisNode(Node node)
{
Node neighbours_North = TryNode(node.x, node.y + 1);
Node neighbours_South = TryNode(node.x, node.y - 1);
double a = Math.Min(neighbours_North.distance,neighbours_South.distance);
Node neighbours_West = TryNode(node.x - 1, node.y);
Node neighbours_East = TryNode(node.x + 1, node.y);
double b = Math.Min(neighbours_West.distance, neighbours_East.distance);
double T = CalculateDistance(a, b);
return node;
}
private Node TryNode(int x, int y)
{
Node node;
try
{
node = nodes[x - 1][y - 1];
}
catch (ArgumentOutOfRangeException)
{
node = new Node()
{
// присваиваем макс. большое значение
distance = double.PositiveInfinity
};
}
return node;
}
public double CalculateDistance(double a, double b)
{
// блок с формулами (2)
double F = 1;
double T;
if(F > Math.Abs(a - b))
{
T = (a + b + Math.Sqrt(2 * 1/F * 1/F - (a-b)*(a-b) )) / 2;
}
else
{
T = 1/F*1/F + Math.Min(a, b);
}
return T;
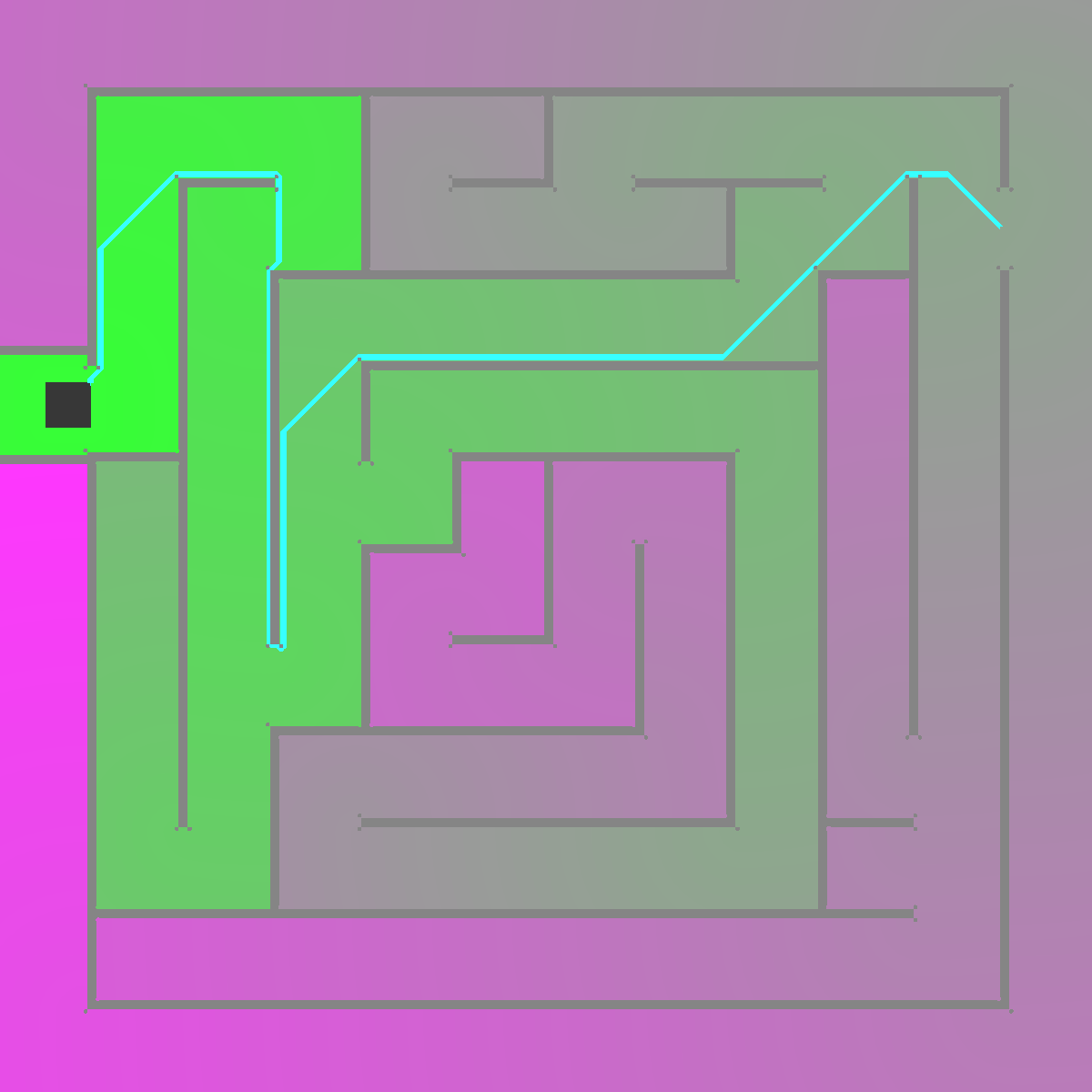
}Я взял картинку из Интернета и преобразовал изображение в узлы. Стенки лабиринта пометил как BLOCK, то есть узлы которые не могут использоваться для создания пути и расчёта расстояний. Цвет меняется от зелёного к фиолетовому. Учитывайте, что все значения distance при рендере нормализуются, поэтому сравнивать два разных рисунка нельзя.

Из рисунка видно, что дольше всего идти до центра лабиринта и до другой стороны перегородки в начале.
Поиск кратчайшего пути до точки
Для поиска кратчайшего пути, мы будем идти в обратную сторону - от точки назначения до исходной. Мы будем перемещаться по узлам по определённому правилу. Путь из посещённых узлов и будет кратчайшим.
Нам нужно отбирать узлы, где значение distance уменьшается, и из них выбирать узлы с наименьшим значением distance. Мы продолжаем идти по узлам, пока не попадём на исходный узел(он имеет значение distance = 0).
Node way_node = target_node; // target node это узел до которого нужно рассчитать путь
while (way_node.distance != 0)
{
way_node = GetNextWayNode(way_node); // получаем следующий узел
way_nodes.Add(way_node); // помещаем узел в "узлы пути"
}
AddSizeWayLine(3);Для поиска узла с наименьшим значением distance помещаем соседние узлы в бинарную кучу.
private Node GetNextWayNode(Node node)
{
int x = node.x - 1;
int y = node.y - 1;
List<Node> neighbours = new List<Node>();
Node node_1 = TryGetNeighbourNode(x, y + 1); // top
Node node_2 = TryGetNeighbourNode(x + 1,y + 1); //top-right
Node node_3 = TryGetNeighbourNode(x + 1,y); // right
Node node_4 = TryGetNeighbourNode(x + 1, y - 1); //down-right
Node node_5 = TryGetNeighbourNode(x, y - 1); // down
Node node_6 = TryGetNeighbourNode(x - 1, y - 1); // down-left
Node node_7 = TryGetNeighbourNode(x - 1, y); //left
Node node_8 = TryGetNeighbourNode(x - 1, y + 1); // top-left
neighbours.Add(node_1);
neighbours.Add(node_2);
neighbours.Add(node_3);
neighbours.Add(node_4);
neighbours.Add(node_5);
neighbours.Add(node_6);
neighbours.Add(node_7);
neighbours.Add(node_8);
foreach (Node node_max in neighbours)
{
// проверяем что distance этого узла меньше чем у узла пути, и узел существует
if(node_max.distance < node.distance && node_max.distance != -1)
{
binaryHeapNode.add(node_max); // добавляем в бинарную кучу
}
}
Node node_next = binaryHeapNode.getMinimum(); // получаем следующий узел из кучи
binaryHeapNode.heapify(0); // перестраиваем кучу после удаления узла
return node_next;
}
private Node TryGetNeighbourNode(int x, int y)
{
Node node = new Node();
try
{
node = nodes[x][y];
}
catch (ArgumentOutOfRangeException)
{
node.distance = -1; // если узла не существует, то присваиваем значение -1
}
return node;
}Если брать путь в 1 пиксель, то путь будет очень тонким и его будет тяжело увидеть. Поэтому увеличим ширину пути с помощью функции AddSizeWayLine()
private void AddSizeWayLine(int size)
{
foreach(Node way_node in way_nodes) // берём узлы пути
{
List<Node> nodes_neighbours = new List<Node>();
int node_x = way_node.x - 1;
int node_y = way_node.y - 1;
for(int i = 1; i <= size; i++) // берём соседние узлы пути
{
Node node_1 = nodes[node_x][node_y + i];
Node node_2 = nodes[node_x + i][node_y];
Node node_3 = nodes[node_x][node_y - i];
Node node_4 = nodes[node_x - i][node_y];
nodes_neighbours.Add(node_1);
nodes_neighbours.Add(node_2);
nodes_neighbours.Add(node_3);
nodes_neighbours.Add(node_4);
}
foreach(Node neighbour in nodes_neighbours) // присваиваем узлам статус WAY
{
if(neighbour.state == StateNode.KNOWN) // проверяем, что узлы не BLOCK
{
Node new_node = neighbour;
new_node.state = StateNode.WAY;
nodes[neighbour.x - 1][neighbour.y - 1] = new_node;
}
}
}
}
Расчёт ошибки вычислений
Для расчёта ошибки возьмём точку по центру и рассчитаем расстояние с помощью алгоритма.
Результат работы алгоритма:

Для расчёта реального расстояния будем использовать теорему Пифагора:
Node know_node; // наша точка в центре, от которой рассчитывается расстояние
private double CalculateErrorThisNode(Node node)
{
double real_distance = CalculateRealDistance(node); // расчёт реального расстояния
double error = Math.Abs(real_distance - node.distance); // расчёт ошибки
return error;
}
private double CalculateRealDistance(Node node)
{
double real_distance = Math.Sqrt((node.x - know_node.x) * (node.x - know_node.x)
+ (node.y - know_node.y) * (node.y - know_node.y));
return real_distance;
}
Видно, что 0 ошибка(белый цвет) на горизонталях и вертикалях, а максимальная ошибка (фиолетовый) на диагоналях.
Пример преобразования изображения в узлы
struct Pixel
{
public byte r, g, b, a;
public int x, y;
}
public List<List<Node>> GetListNodes() { return nodes; }
public void ConvertToNode()
{
byte[] bytes_image = image.Data;
GeneratePixel(bytes_image);
for (int i = 0; i < image.Height; i++)
{
nodes.Add(new List<Node>());
for (int j = 0; j < image.Width; j++)
{
Node node = new Node()
{
x = i+1,
y = j+1,
distance = double.PositiveInfinity,
state = StateNode.FAR
};
// получаем пиксель соотвествующий данному узлу
Pixel pixel = pixels[image.Height * (j) + i];
// ищем пиксели не белого цвета и помечаем их как KNOWN
// в моём случае чёрное изображение на белом фоне
if (pixel.r != 255 || pixel.g != 255 || pixel.b != 255)
{
node.state = StateNode.KNOWN;
}
nodes[i].Add(node);
}
}
}
private void GeneratePixel(byte[] bytes_image)
{
int index_pixel = 0;
int x = 1, y = 1;
for (int i = 0; i < bytes_image.Length; i += 4)
{
Pixel pixel = new Pixel()
{
r = bytes_image[i],
g = bytes_image[i + 1],
b = bytes_image[i + 2],
a = bytes_image[i + 3],
x = x,
y = y
};
index_pixel++;
x++;
if (index_pixel % image.Height == 0)
{
y++;
x = 1;
}
pixels.Add(pixel);
}
}Другие интересные результаты работы алгоритма


Источники
R. Kimmel and J.A. Sethian (1996). Fast Marching Methods for Computing Distance Maps and Shortest Paths.
Jakob Andreas Bærentzen (2001). On the implementation of fast marching methods for 3D lattices.
Dieuwertje Alblas (2018). Implementing and analysing the fast marching method
Комментарии (10)

Zara6502
12.01.2024 11:32+3А почему не так как я показал по черным пунктирам? Или это графическая условность? Тогда, по идее, нужно рисовать от центров квадратов.


omysov Автор
12.01.2024 11:32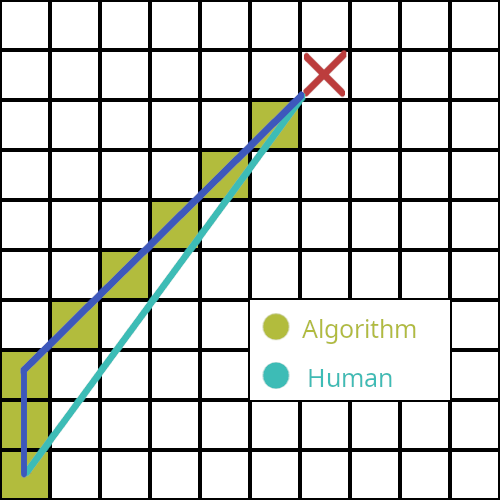
Расчёт пути Алгоритм идёт от пикселя к пикселю, поэтому пути получаются соответствующие. На картинке выше, я показал в чём разница "человеческого" и "компьютерного" пути. Если мы возьмём рисунок и просто проведём линию, то получим "истинный" короткий путь.
В статье я рассчитывал абсолютную ошибку, и можно заметить, что на диагоналях она формируется максимальная.

Zara6502
12.01.2024 11:32+1Алгоритм идёт от пикселя к пикселю, поэтому пути получаются соответствующие
То что я нарисовал всё равно более оптимальный маршрут от пикселя к пикселю.
На картинке выше, я показал в чём разница "человеческого" и "компьютерного" пути
Не-не-не, для адаптации прямой на сетчатой поверхности есть алгоритм Брезенхэма. Но и даже его вы не использовали на той картинке где я нарисовал черным пунктиром. Там у вас достаточно пикселей чтобы двигаться по пунктиру. ЛИБО, как я и отметил выше, вы изначально неверно отобразили работу алгоритма, если вы за пиксель считаете просто один квадрат лабиринта, тогда вам нужно соединять центры квадратов, а не рисовать тонкие линии вдоль стен.
В статье я рассчитывал абсолютную ошибку, и можно заметить, что на диагоналях она формируется максимальная.
Пардон, но я не готов обсуждать сам алгоритм.

wataru
12.01.2024 11:32на сетчатой поверхности есть алгоритм Брезенхэма
На самом деле, алгоритм Брезенхема даст путь такой же длины. Он же только на 8 соседних клеток может переходить. Значит там все ребра будут или по диагонали, или вдоль сетки. От перестановки слагаемых сумма не меняется, т.ч. можно сначала все вертикальные шажки сделать, а только потом все диагональные. На прямую вообще не похоже, но длина пути по пикселям та же самая.

Zara6502
12.01.2024 11:32На самом деле, алгоритм Брезенхема даст путь такой же длины
Ну я к длине не особо и прикапываюсь. Я о самом характере построения маршрута. Запустите в этот лабиринт A* и посмотрите как он построит. Просто во второй картинке что заставит алгоритм сделать два шага вверх? Мне кажется логичным сразу идти по диагонали или у вас вес диагонального шага тоже равен 1?
Посмотрел по формулам, у вас distance это скорее steps, то есть число шагов. Формально шагов вы сделаете столько же, но все равно непонятно почему ваш алгоритм жмётся к стенкам а не идёт по прямой.

wataru
12.01.2024 11:32Он может сделать сначала все шаги по диаганали, потому что это в сторону конца, а потом все по вертикали, потому что только в ту сторону кратчайший путь.
Кстати, я не автор. Похоже, у автора в статье расстояние - это именно длина пути вдоль сетки с 8 соседями. С корнями и вещественными числами.
Вдоль стенок алгоритм жмется потому, что ребра в каждой вершине перебираются в одном и том же порядке, без перемешивания и дополнительного рандома. Если и туда и сюда расстояние в итоге будет одинаковое, то берется первое попашееся. И это первое попавшееся - всегда в одну и ту же сторону, пока или до стенки не дойдет путь, или оставшийся путь не станет из одних только диагональных кусочков, и оптимальное направление не изменится.
Какой-нибуть обход в ширину или дейкстра на такой сетке найдут примерно такой же путь.

omysov Автор
12.01.2024 11:32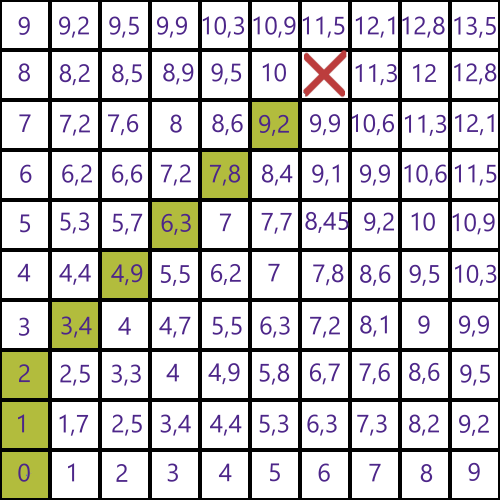
значение distance узлов. Значение округлены Сначала алгоритм рассчитывает поля расстояний, а затем, используя их, рассчитывает кратчайший путь. Пример на картинке.

wataru
12.01.2024 11:32Какой-то гибрид обхода в ширину и Дейкстры с кучей получился. Как уже заметили выше - пути оно ищет не кратчайшие. Чем оно лучше обхода в ширину по 8 соседним точкам? Оно точно медленнее а пути найдет такие же. На картинках с линиями еще и пути будут оптимальными.
Раз уж вы про алгоритм пишите, то опишите хотя бы его ассимтотическую сложность, сравните с другими алгоритмами, опишите где и когда он применим.

omysov Автор
12.01.2024 11:32Спасибо за замечания. FMM в своей основе имеет алгоритм Дейкстры, но отличается от него способом расчета значений узлов(смотрите мат. описание). FMM легко расширяем, в отличие от Дейкстры. Я видел как в одной работе FMM использовали на триангулированной поверхности для рассчёта полей расстояний.
В этой статье у меня не было цели сравнивать алгоритмы. В рунете очень мало информации о FMM, и я решил это исправить.




Zara6502
и более про стороны свет в статье мы не услышим )
Так же непонятно в чем простота, если переменные даже не назвали как Vn, Vw, Vs, Ve.