В этой статье наши инженеры хотели бы поделиться с Хабром достаточно интересным инструментом, который можно эффективно применять для фильтрации зашумленных сигналов, пользуясь априорным знанием об унимодальности сигнала.
Задача оффлайновой фильтрации сигналов в случае, когда ожидаемая форма сигнала известна с точностью до нескольких неизвестных параметров, сводится к задаче аппроксимации. Например, если известно, что сигнал линейно растет на рассматриваемом промежутке, задача сведётся к линейной регрессии, а если можно предположить, что шум — нормален, то правильным методом будет МНК. Но однажды мы столкнулись с задачей оценки формы профиля рентгеновского микрозонда (пучка), про которую априори было достоверно известно только одно: профиль унимодален, а именно имеет ровно один максимум. Оказывается, и в этом случае можно наилучшим (в смысле, например, L2 метрики) образом приблизить экспериментальный сигнал функцией, принадлежащей известному множеству (множеству унимодальных функций). Причём — с приемлемой ассимптотикой вычислительной сложности.
 ===>
===>  ===>
===> 
Итак, речь пойдёт о задаче аппроксимации некоторого зашумлённого сигнала как функции дискретного аргумента
как функции дискретного аргумента  , причем известно, что исходный сигнал — унимодальный. В рассматриваемом случае дополнительно известно, что на краях сигнал ассимптотически приближается к нулю. Следует отметить, что рассматриваемый ниже метод сам по себе не требует такого допущения.
, причем известно, что исходный сигнал — унимодальный. В рассматриваемом случае дополнительно известно, что на краях сигнал ассимптотически приближается к нулю. Следует отметить, что рассматриваемый ниже метод сам по себе не требует такого допущения.
Вначале, для простоты изложения, имеет смысл рассмотреть ту же задачу для монотонной функции. Описание приведено для монотонно нестрого возрастающей функции, хотя, разумеется, для монотонно убывающей можно проделать всё то же самое.
Если предположить, что шум нормально распределен, то задача сведётся к минимизации квадратичного функционала%20-%20Y(X_i))%5E2%7D) в присутствии неравенств вида
в присутствии неравенств вида %20%5Cge%20%5Cwidetilde%7BY%7D(X_i)) . Это — задача квадратичного программирования, и для нее на просторах интернета можно найти некоторое количество готовых решателей. Но, во-первых, задача квадратичного программирования в общем случае обсчитывается довольно медленно, а во-вторых, задача аппроксимации унимодального сигнала не выписывается в подобном виде, если положение экстремума не известно заранее.
. Это — задача квадратичного программирования, и для нее на просторах интернета можно найти некоторое количество готовых решателей. Но, во-первых, задача квадратичного программирования в общем случае обсчитывается довольно медленно, а во-вторых, задача аппроксимации унимодального сигнала не выписывается в подобном виде, если положение экстремума не известно заранее.
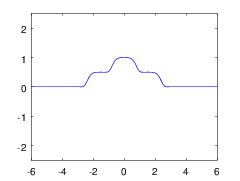
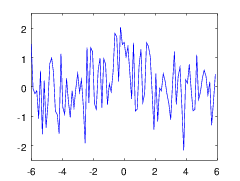
Существует альтернативное решение, не обладающее указанными недостатками, но при его использовании шкалу сигнала придётся считать дискретной. Тут стоит отметить, что задача не интересна в случае слабого шума, поскольку обычная линейная фильтрация, скорее всего, снимет все практические проблемы. Что же такое интересный, сильный шум? На рис. 1 можно увидеть модельный сигнал до и после такого зашумления. Шум здесь задан нормальным распределением
придётся считать дискретной. Тут стоит отметить, что задача не интересна в случае слабого шума, поскольку обычная линейная фильтрация, скорее всего, снимет все практические проблемы. Что же такое интересный, сильный шум? На рис. 1 можно увидеть модельный сигнал до и после такого зашумления. Шум здесь задан нормальным распределением ) . В подобных условиях дискретизация аппроксимирующего сигнала не выглядит существенной потерей. Кроме того, как будет видно далее, при увеличении числа отсчетов сложность вычислений будет возрастать линейно.
. В подобных условиях дискретизация аппроксимирующего сигнала не выглядит существенной потерей. Кроме того, как будет видно далее, при увеличении числа отсчетов сложность вычислений будет возрастать линейно.

Рис. 1: a) Модельный монотонный сигнал до налолжения шума. b) Модельный монотонный сигнал после наложения шума.
Оказывается, в дискретном приближении фильтрация нормально зашумленного монотонного сигнала сводится к динамическому программированию с двумя параметрами, причём, пользуясь этим решением, удаётся построить вычислительную схему той же сложности и для унимодального случая.
О том, что такое динамическое программирование, можно почитать здесь, а как и к каким задачам его применяют — здесь.
В рассматриваемой задаче таблица динамического программирования — двумерная, её столбцам i соответствуют возрастающие слева направо значения дискретного аргумента экспериментальных точек, а строкам j — возрастающие снизу вверх возможные значения аппроксимирующей функции
экспериментальных точек, а строкам j — возрастающие снизу вверх возможные значения аппроксимирующей функции  . Минимизируемый функционал — сумма квадратов отклонений
. Минимизируемый функционал — сумма квадратов отклонений  от
от  вдоль путей с допустимыми переходами. Очевидно, что допустимыми будут переходы на 1 вправо с одновременным неотрицательным смещением вверх.
вдоль путей с допустимыми переходами. Очевидно, что допустимыми будут переходы на 1 вправо с одновременным неотрицательным смещением вверх.
Внешний цикл ведётся по координате i слева направо. Для каждого значения выполняется внутренний цикл по координате j снизу вверх. Минимальное значение функционала определяется по формуле
выполняется внутренний цикл по координате j снизу вверх. Минимальное значение функционала определяется по формуле
%20%2B%20(Y_j%20-%20%5Cwidetilde%7BY%7D_j)%5E2%2C%0A)
причём за пределами таблицы функционал считается равным нулю.
При этом, чтобы не пересчитывать каждый раз минимум на меньших значениях j, его полезно сохранять в процессе заполнения вместе со значением функционала, а поскольку в конце требуется восстановить путь, сохранять удобнее значение m, на котором этот минимум был достигнут:

Тогда вычисление самого функционала можно выполнять за O(1) для каждой ячейки:
%5E2.%0A)
После завершения прямого прохода остаётся получить аппроксимацию в явном виде. Для этого ищется минимум среди значений функционала для крайнего правого столбца (столбца с наибольшей координатой i), а затем выполняется обратный проход по i, с восстановлением индекса значения отфильтрованного сигнала j* в каждом столбце:
%2C%20%26%20i%20%3D%20n%20-%201%20%5C%5C%0Am_%7Bi%2Cj%5E*_%7Bi%2B1%7D%7D%2C%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%26%20i%20%3C%20n%20-%201%0A%5Cend%7Bcases%7D%0A)
Окончательные значения определяются как
определяются как
%20%3D%20%5Cwidetilde%7BY%7D_%7Bj%5E*_i%7D%0A)
На рис. 2 показан пример результата описанного алгоритма для монотонного сигнала.
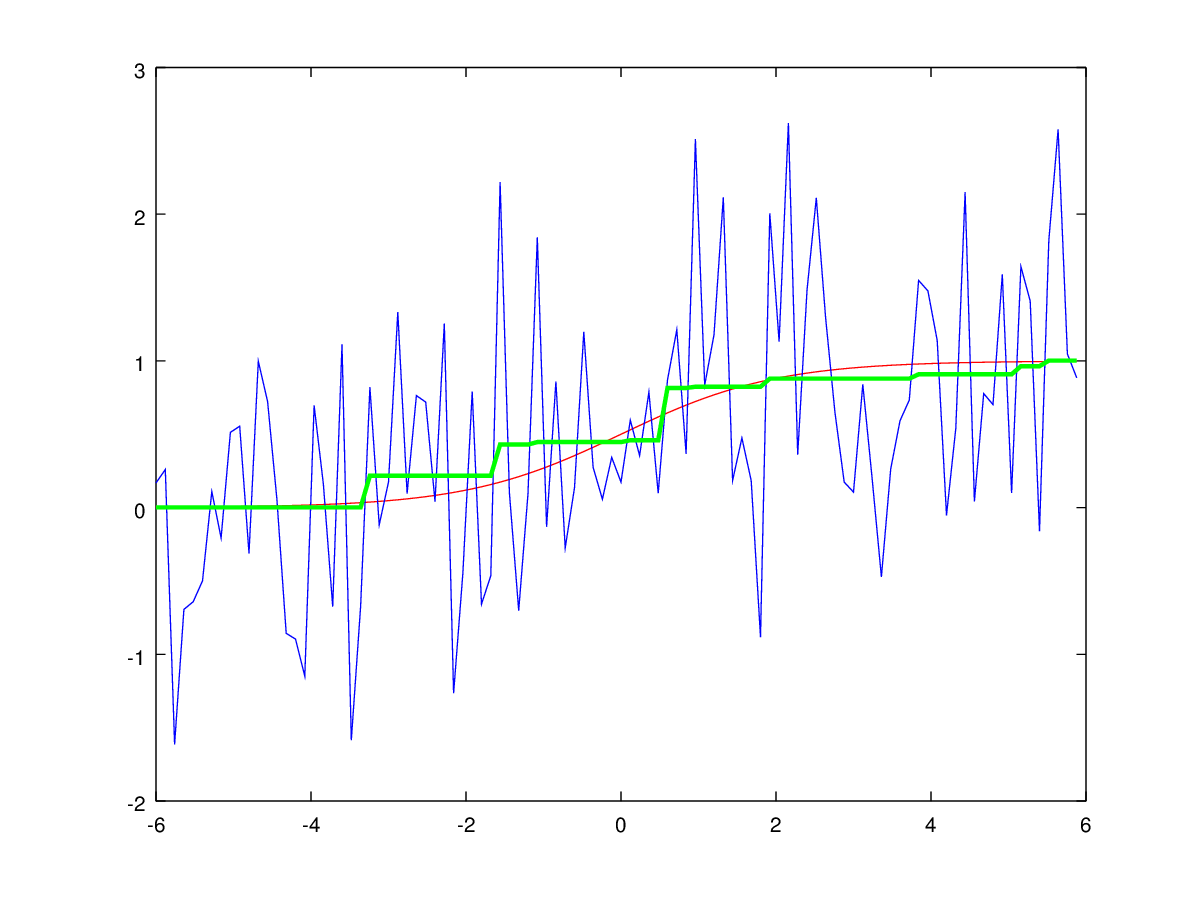
Рис. 2: Фильтрация монотонно возрастающего сигнала динамическим программированием. Синим цветом показан входной зашумлённый сигнал, зелёным — результат работы алгоритма, красным — идеальный незашумлённый сигнал.
На этом рассмотрение вспомогательного монотонного случая закончено.
Используя полученный результат, можно решить задачу об унимодальном сигнале, заполнив 2 таблицы ДП: одна заполняется как для монотонной функции, вторая — таким же образом, но в обратную сторону. В результате вычисляется 2 функционала: и
и  , а также значения
, а также значения  и
и  для восстановления путей по таблицам. После этого среди всех значений i и j ищется такоая пара
для восстановления путей по таблицам. После этого среди всех значений i и j ищется такоая пара ) , для которой сумма функционалов минимальна — это будут индексы максимума аппроксимированной функции. Значения функции с каждой стороны от него восстанавливаются по соответствующей таблице.
, для которой сумма функционалов минимальна — это будут индексы максимума аппроксимированной функции. Значения функции с каждой стороны от него восстанавливаются по соответствующей таблице.
%20%3D%20%5Coperatornamewithlimits%7Bargmin%7D%5Climits_%7Bi%2C%20j%7D(W%5E%7Blr%7D_%7Bi%2C%20j%7D%20%2B%20W%5E%7Brl%7D_%7Bi%2C%20j%7D)%0A)

%20%3D%20%5Cwidetilde%7BY%7D_%7Bj%5E*_i%7D%0A)
На рисунках 3 и 4 показан пример исходного унимодального сигнала и результата его обработки предложенным алгоритмом.

Рис. 3: Зашумлённый унимодальный сигнал.
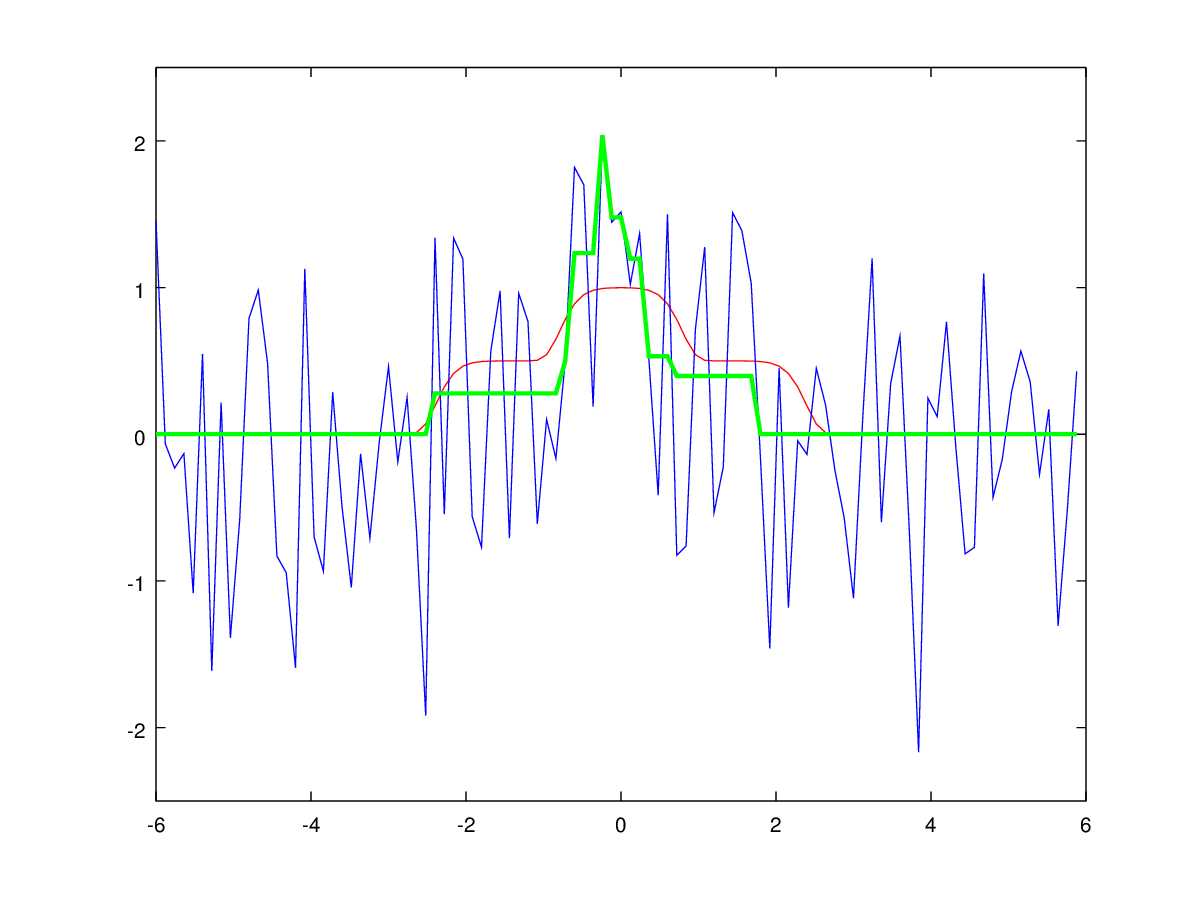
Рис. 4: Фильтрация унимодального сигнала динамическим программированием. Синим цветом показан входной зашумлённый сигнал, зелёным — результат работы алгоритма, красным — идеальный незашумлённый сигнал.
В случае, если известно, что сигнал не может меняться быстрее некоторой фиксированной скорости (что вполне вероятно), точность регрессии можно улучшить, введя это ограничение в алгоритм в явном виде. Для этого достаточно вычислить максимально возможное изменение индекса значения сигнала
(что вполне вероятно), точность регрессии можно улучшить, введя это ограничение в алгоритм в явном виде. Для этого достаточно вычислить максимально возможное изменение индекса значения сигнала  для каждого i и запретить переходы в таблице ДП с изменением j более, чем на эту величину:
для каждого i и запретить переходы в таблице ДП с изменением j более, чем на эту величину:
%20%2F%20(%5Cwidetilde%7BY%7D_%7B1%7D%20-%20%5Cwidetilde%7BY%7D_%7B0%7D)%5Crceil%0A)
%20%2B%20(%5Cwidetilde%7BY%7D_%7Bj%7D%20-%20Y_%7Bj%7D)%5E2%0A)
Правда, чтобы не проиграть в трудоёмкости, нужно иметь возможность получать минимальное значение функционала на отрезке [j — dj, j] за константное время.
Это можно сделать с помощью алгоритма Ван Херка — Гила — Вермана, описанного, например, здесь.
Результат применения алгоритма с ограничением на производную показан на рис. 5.
показан на рис. 5.
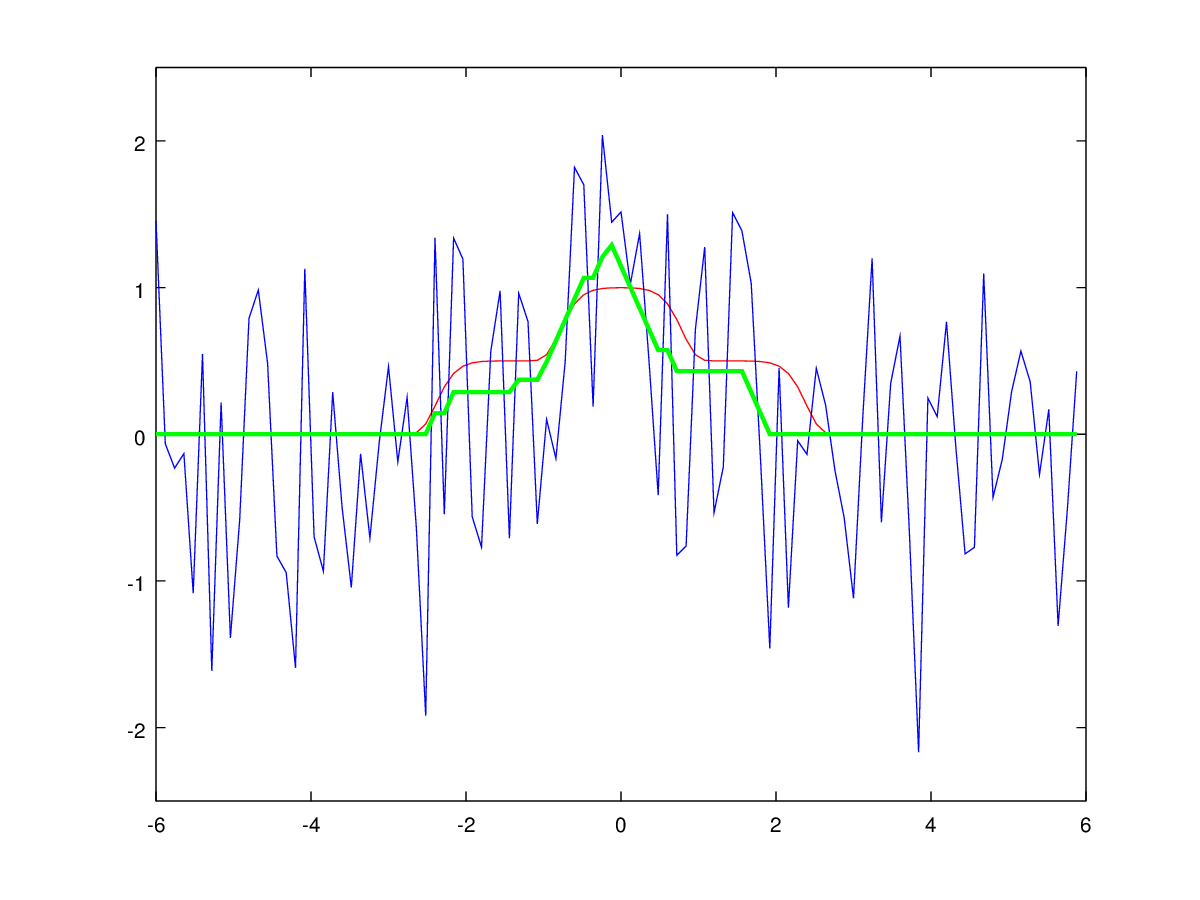
Рис. 5: Фильтрация унимодального сигнала динамическим программированием с ограничением на скорость изменения сигнала. Синим цветом показан входной зашумлённый сигнал, зелёным — результат работы алгоритма, красным — идеальный незашумлённый сигнал.
Пытливый читатель может заподозрить, что таких же или лучших результатов можно достигнуть более простыми способами. Конечно, при определённых параметрах сигнала и шума описанная техника будет излишней. Кроме того, короче та дорога, которую знаешь. Поэтому на каждый хитрый случай у специалиста наверняка найдётся любимый метод, который именно в его руках даст приемлемый результат.
Чтобы рассеять ощущение возможного мошенничества, на рис. 6 и 7 приведены примеры обработки сигнала гауссовским сглаживанием и медианной фильтрацией с зашкаливанием в нуле. Параметры фильтров подбирались с целью получения оптимального результата, но без фанатизма.
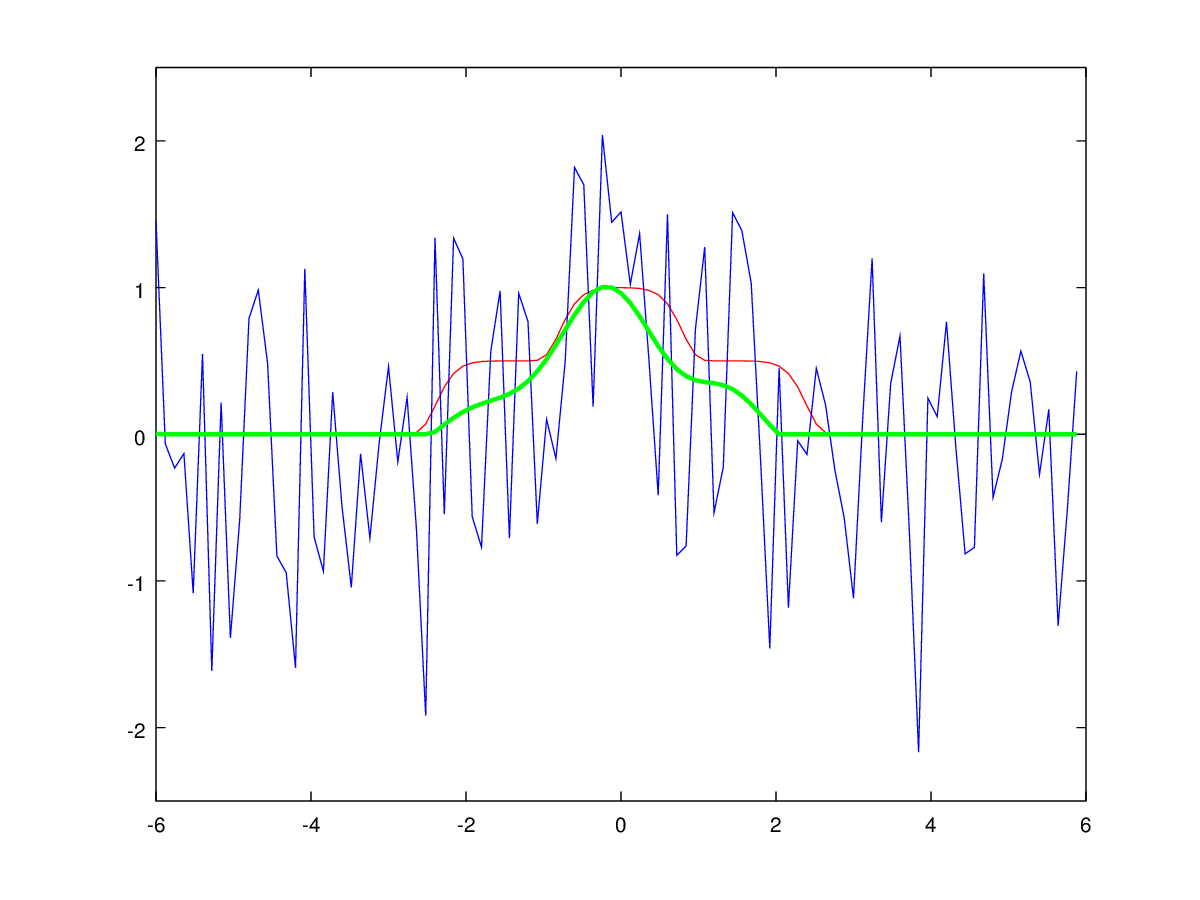
Рис. 6: Фильтрация унимодального сигнала гауссовским сглаживанием. Синим цветом показан входной зашумлённый сигнал, зелёным — результат фильтрации, красным — идеальный незашумлённый сигнал.
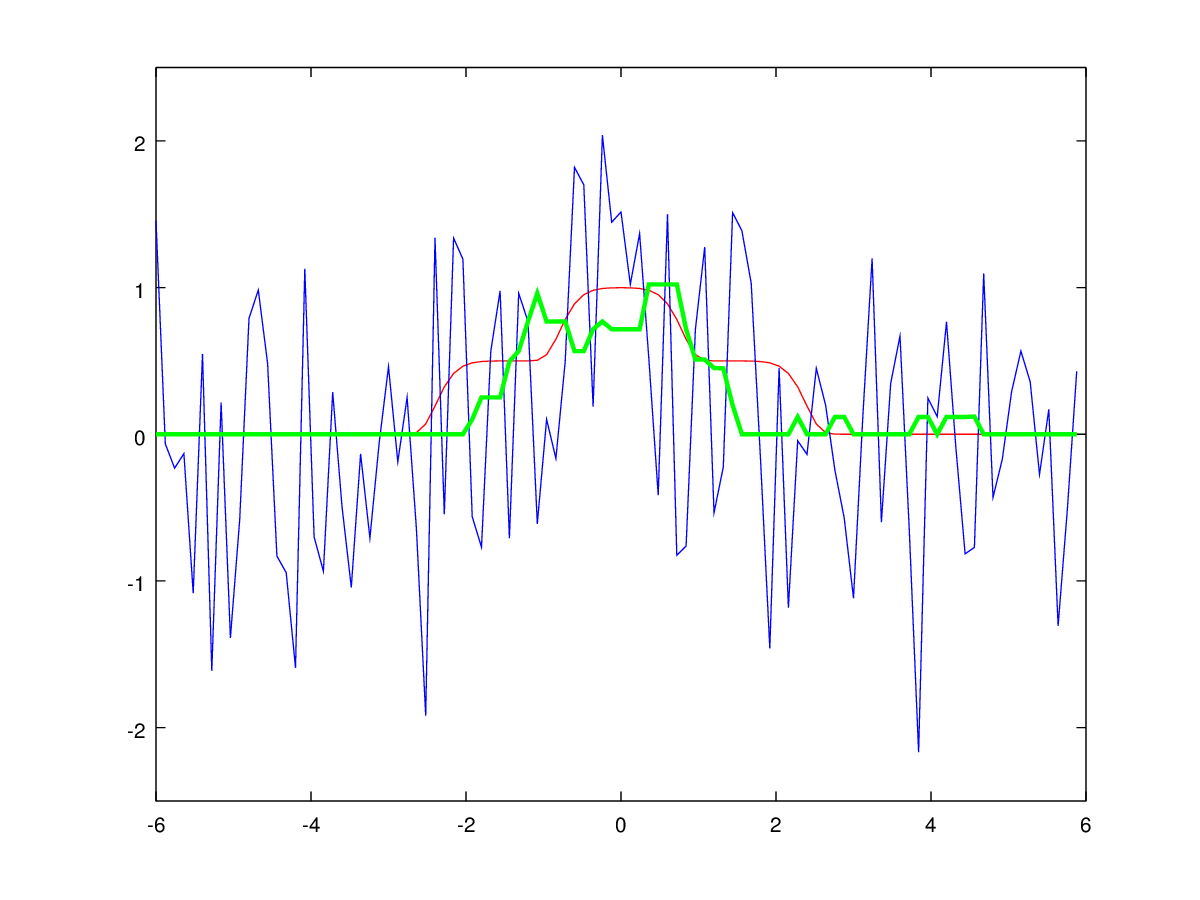
Рис. 7: Медианная фильтрация унимодального сигнала. Синим цветом показан входной зашумлённый сигнал, зелёным — результат фильтрации, красным — идеальный незашумлённый сигнал.
Как видно, на достаточно произвольных данных метод динамического программирования дает результат получше, чем простейшие общеизвестные фильтры. При этом сравнивать их на модельных примерах подробно — абсолютно бессмысленно. Изложенный выше метод ценен ровно тем, что является примером “костюма, сшитого по мерке”: формализованная постановка задачи была положена в саму основу метода. В рассматриваемом случае это было условие унимодальности. Аналогично, линейные методы “по мерке” сигналам, частотно разделимым с шумом. Еще один инструмент в наборе — что может быть лучше для инженера?
Задача оффлайновой фильтрации сигналов в случае, когда ожидаемая форма сигнала известна с точностью до нескольких неизвестных параметров, сводится к задаче аппроксимации. Например, если известно, что сигнал линейно растет на рассматриваемом промежутке, задача сведётся к линейной регрессии, а если можно предположить, что шум — нормален, то правильным методом будет МНК. Но однажды мы столкнулись с задачей оценки формы профиля рентгеновского микрозонда (пучка), про которую априори было достоверно известно только одно: профиль унимодален, а именно имеет ровно один максимум. Оказывается, и в этом случае можно наилучшим (в смысле, например, L2 метрики) образом приблизить экспериментальный сигнал функцией, принадлежащей известному множеству (множеству унимодальных функций). Причём — с приемлемой ассимптотикой вычислительной сложности.
 ===>
===>  ===>
===> 
Итак, речь пойдёт о задаче аппроксимации некоторого зашумлённого сигнала
Вначале, для простоты изложения, имеет смысл рассмотреть ту же задачу для монотонной функции. Описание приведено для монотонно нестрого возрастающей функции, хотя, разумеется, для монотонно убывающей можно проделать всё то же самое.
Если предположить, что шум нормально распределен, то задача сведётся к минимизации квадратичного функционала
Существует альтернативное решение, не обладающее указанными недостатками, но при его использовании шкалу сигнала

Рис. 1: a) Модельный монотонный сигнал до налолжения шума. b) Модельный монотонный сигнал после наложения шума.
Оказывается, в дискретном приближении фильтрация нормально зашумленного монотонного сигнала сводится к динамическому программированию с двумя параметрами, причём, пользуясь этим решением, удаётся построить вычислительную схему той же сложности и для унимодального случая.
О том, что такое динамическое программирование, можно почитать здесь, а как и к каким задачам его применяют — здесь.
Фильтрация монотонного сигнала методом динамического программирования
В рассматриваемой задаче таблица динамического программирования — двумерная, её столбцам i соответствуют возрастающие слева направо значения дискретного аргумента
Внешний цикл ведётся по координате i слева направо. Для каждого значения
причём за пределами таблицы функционал считается равным нулю.
При этом, чтобы не пересчитывать каждый раз минимум на меньших значениях j, его полезно сохранять в процессе заполнения вместе со значением функционала, а поскольку в конце требуется восстановить путь, сохранять удобнее значение m, на котором этот минимум был достигнут:
Тогда вычисление самого функционала можно выполнять за O(1) для каждой ячейки:
После завершения прямого прохода остаётся получить аппроксимацию в явном виде. Для этого ищется минимум среди значений функционала для крайнего правого столбца (столбца с наибольшей координатой i), а затем выполняется обратный проход по i, с восстановлением индекса значения отфильтрованного сигнала j* в каждом столбце:
Окончательные значения
На рис. 2 показан пример результата описанного алгоритма для монотонного сигнала.

Рис. 2: Фильтрация монотонно возрастающего сигнала динамическим программированием. Синим цветом показан входной зашумлённый сигнал, зелёным — результат работы алгоритма, красным — идеальный незашумлённый сигнал.
На этом рассмотрение вспомогательного монотонного случая закончено.
Унимодальный сигнал
Используя полученный результат, можно решить задачу об унимодальном сигнале, заполнив 2 таблицы ДП: одна заполняется как для монотонной функции, вторая — таким же образом, но в обратную сторону. В результате вычисляется 2 функционала:
На рисунках 3 и 4 показан пример исходного унимодального сигнала и результата его обработки предложенным алгоритмом.

Рис. 3: Зашумлённый унимодальный сигнал.

Рис. 4: Фильтрация унимодального сигнала динамическим программированием. Синим цветом показан входной зашумлённый сигнал, зелёным — результат работы алгоритма, красным — идеальный незашумлённый сигнал.
Ограничение на производную
В случае, если известно, что сигнал не может меняться быстрее некоторой фиксированной скорости
Правда, чтобы не проиграть в трудоёмкости, нужно иметь возможность получать минимальное значение функционала на отрезке [j — dj, j] за константное время.
Это можно сделать с помощью алгоритма Ван Херка — Гила — Вермана, описанного, например, здесь.
Результат применения алгоритма с ограничением на производную

Рис. 5: Фильтрация унимодального сигнала динамическим программированием с ограничением на скорость изменения сигнала. Синим цветом показан входной зашумлённый сигнал, зелёным — результат работы алгоритма, красным — идеальный незашумлённый сигнал.
Разоблачение чёрной магии
Пытливый читатель может заподозрить, что таких же или лучших результатов можно достигнуть более простыми способами. Конечно, при определённых параметрах сигнала и шума описанная техника будет излишней. Кроме того, короче та дорога, которую знаешь. Поэтому на каждый хитрый случай у специалиста наверняка найдётся любимый метод, который именно в его руках даст приемлемый результат.
Чтобы рассеять ощущение возможного мошенничества, на рис. 6 и 7 приведены примеры обработки сигнала гауссовским сглаживанием и медианной фильтрацией с зашкаливанием в нуле. Параметры фильтров подбирались с целью получения оптимального результата, но без фанатизма.

Рис. 6: Фильтрация унимодального сигнала гауссовским сглаживанием. Синим цветом показан входной зашумлённый сигнал, зелёным — результат фильтрации, красным — идеальный незашумлённый сигнал.

Рис. 7: Медианная фильтрация унимодального сигнала. Синим цветом показан входной зашумлённый сигнал, зелёным — результат фильтрации, красным — идеальный незашумлённый сигнал.
Как видно, на достаточно произвольных данных метод динамического программирования дает результат получше, чем простейшие общеизвестные фильтры. При этом сравнивать их на модельных примерах подробно — абсолютно бессмысленно. Изложенный выше метод ценен ровно тем, что является примером “костюма, сшитого по мерке”: формализованная постановка задачи была положена в саму основу метода. В рассматриваемом случае это было условие унимодальности. Аналогично, линейные методы “по мерке” сигналам, частотно разделимым с шумом. Еще один инструмент в наборе — что может быть лучше для инженера?

0serg
Отличная работа! Буквально недавно писал очень похожую реализацию для немного другой задачи имеющей ценность для софтверного тестирования. Предположим что у нас есть некий дискретный процесс, про который известно что он меняется редко (т.е. вероятность изменения текущего уровня на каждом шагу намного меньше вероятности что уровень останется тем же), но померить который мы можем только с достаточно большой погрешностью. Если считать что погрешость аппроксимируется нормальным распределением, то на выходе получается очень похожая схема :). Правда я без дискретизации обошелся, для гауссова шума это возможно
Вообще в общем случае подобные модели удобно моделировать с помощью байесовских сетей. Там просто в лоб записываются условные вероятности и всё. Просто-напросто пишем что вероятность следующего отсчета если известно значение предыдущего p(x_{n+1}|xn) = 0 если x{n+1}<xn и const если x{n+1}>=x_n, добавляем известные распределения (равномерное для отсчетов x_n, гауссово для шума) и на выходе чисто механически получается сеть для определения монотонного сигнала, которую после дискретизации можно скормить солверу. Дальше делаем две сети — на рост и на убывание и комбинируем. Думать нужно меньше, гибкости больше.
Ну и традиционный МНК для шума работает все же только если шум не просто имеет нормальное распределение, но и независим в соседних отсчетах, а его дисперсия постоянна. "Независим и одинаково распределен в отдельных отсчетах" — логичное и типовое ограничение на шум, но все его стоило упомянуть явно.
Arastas
Вы знаете, я могу что-то неправильно помнить, но, кажется,
1) Если шум взаимонезависим с измерениями и имеет нулевое матожидание, то оценка МНК получится несмещенной, т.е., в моём понимании, МНК будет работать.
2) Если шум при этом еще имеет постоянную дисперсию и не автокорелирован, то оценка МНК является эффективной и наилучшей в классе линейных, Best Linear Unbiased Estimation (BLUE).
Зачем требовать нормального распределения?
0serg
Да, это верно. Нормальное распределение здесь не требуется. Я имел в виду что если шум НЕ независим в отсчетах или имеет изменяющуюся дисперсию (п. 2 нарушен), то он может все равно быть нормальным, но при этом МНК перестанет быть эффективным. На мой взгляд простая несмещенность оценки еще не гарантирует работоспособности, т.к. хотя в среднем метод при миллионе прогонов и даст верный ответ, в каждом конкретном прогоне МНК с "плохим" шумом может давать очень большую погрешность.