29.02.2020 07:32
938MeV 114 22800 Источник
Магнит в медной трубе
Изображение взято с сайта «Популярная механика»

Многие видели опыт с постоянным магнитом, который как бы застревает внутри толстостенной медной трубки. В этой статье будем разбираться в физике процесса.
Сначала запишем формулу магнитного поля постоянного магнита, и посчитаем, какой магнитный поток проходит через поперечное сечение трубы, потом заставим магнитик двигаться и узнаем, какой возникает индуцированный электрический ток в металле, какова рассеиваемая электрическая мощность, запишем и решим уравнение движения постоянного магнита.

И если вы дочитали до этого места и не испугались, добро пожаловать под кат — дальше будет интереснее!

Сам я давно подумывал над тем, чтобы хорошенько разобраться в этом вопросе. И вот недавно зашёл разговор с коллегой по работе. Его ребёнку задали сделать научную демонстрацию в школе, на что папа раздобыл кусок медной трубы и неодим-железо-борный магнит. Ребёнок разобрался, произвёл демонстрацию опыта перед классом, дал пояснения, но ни класс ни учитель особо не впечатлились. На конкурсе научных опытов победил вулкан (!) из соды и лимонной кислоты =) Мы с коллегой прикинули на словах и поняли, что дело ясное, что дело тёмное. Да и в литературе не особо много написано по данной тематике. Поговорили и разошлись. Ну а я всё-таки решил попробовать продраться сквозь дебри. В этой статье пишу, что у меня получилось.

Описание эксперимента



Начнём с просмотра видео с демонстрацией опыта. Прежде чем углубиться в теорию, будет полезно представить картину происходящего в общем. В интернете этот опыт был объяснён и продемонстрирован на видео много раз. Но мне тоже нужно его здесь описать, чтобы далее было понятно, от чего мы отталкиваемся.

Экспериментатор помещает постоянный магнит в виде небольшого шарика в медную трубу, которую он держит вертикально. Вопреки ожиданиям, шарик не падает сквозь трубу с ускорением свободного падения, а движется внутри трубы гораздо медленнее.

Итак, в опыте мы наблюдаем, как постоянный магнит движется внутри полой медной трубы с постоянной скоростью. Зафиксируем произвольную точку в теле медной трубки и мысленно проведем поперечное сечение. Через данное сечение медной трубы проходит магнитный поток, создаваемый постоянным магнитом. Из-за того, что магнит движется вдоль трубы, в сечении проводника возникает переменный магнитный поток, то ли нарастающий, то ли убывающий в зависимости от того, приближается или отдаляется магнит от точки, где мы мысленно провели сечение. Переменный магнитный поток, согласно уравнениям Максвелла, порождает вихревое электрическое поле, вообще говоря, во всём пространстве. Однако, только там, где есть проводник, это электрическое поле приводит в движение свободные заряды, находящиеся в проводнике — возникает круговой электрический ток, который создает уже своё собственное магнитное поле и взаимодействует с магнитным полем движущегося постоянного магнита. Проще говоря, круговой электрический ток создает магнитное поле того же знака, что и постоянный магнит, и на магнит действует некая диссипативная сила, а если конкретно — сила трения. Читатель может справедливо задать вопрос: «Трение чего обо что?» Трение возникает между магнитным полем диполя и проводником. Да, это трение не механическое. Вернее сказать, тела не соприкасаются. Ну и пусть! Трение всё равно есть!

В целом, на словах всё выглядит более или менее складно, а можно ли это описать на языке математики? Приступим…

Математическое описание


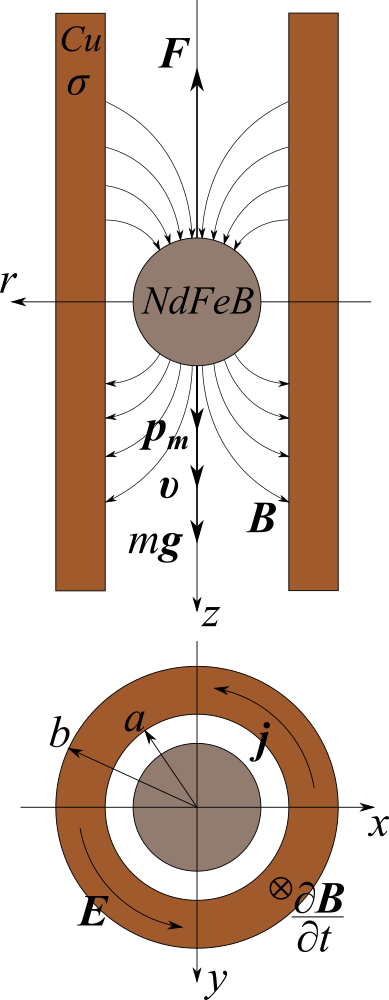
Постоянный магнит в медной трубе

Перво-наперво, нам понадобится математическая модель постоянного магнита. На мой взгляд, будет удобно представить постоянный магнит как магнитный диполь.

$\vec{B}=\frac{\mu_0}{4\pi}\left(\frac{3(\vec{p}_m\cdot\vec{r})\vec{r}}{r^5}-\frac{\vec{p}_m}{r^3}\right)$


Здесь приняты обозначения $\vec{r}=(r,z)$ — радиус-вектор из центра диполя в точку наблюдения, $\vec{p}_m$ — вектор дипольного момента.

Далее, нам нужно записать $z$-компоненту вектора магнитной индукции для вычисления магнитного потока, захваченного в поперечном сечении металла медной трубы. Выпишем $z$-компоненту магнитного поля здесь

$B_z(r,z) = \frac{\mu_0\,p_m}{4\pi}\frac{2z^2 - r^2}{\left(r^2 + z^2\right)^\frac{5}{2}}$


Теперь запишем выражение для магнитного потока через площадь, охватываемую окружностью радиуса $r$ на расстоянии $z$ от диполя.

$\Phi(r,z) = \int_0^{2\pi}\int_0^r B_z(r',z)\,r'\,dr'\,d\varphi = 2\pi\int_0^r \frac{\mu_0\,p_m}{4\pi}\frac{2z^2 - r'^2}{\left(r'^2 + z^2\right)^\frac{5}{2}}\,r'\,dr'$


Вы не поверите, но этот интеграл берётся. Не буду утомлять. В ответе получается очень красиво

$\Phi(r,z) = \frac{\mu_0\,p_m}{2}\frac{r^2}{\left(r^2 + z^2\right)^\frac{3}{2}}$


Из-за того, что диполь движется вдоль оси $z$ со скоростью $v$, нужно также сделать стандартную подстановку $\Phi(r, z)\rightarrow \Phi(r, z - v t)$
Похоже, пора призвать на помощь одно из великих уравнений Максвелла, а именно, то самое уравнение, которое описывает закон Фарадея:
Изменение потока магнитной индукции, проходящего через незамкнутую поверхность $S$, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре $L$, который является границей поверхности $S$

$\oint_L \vec{E}\,dl = -\frac{\partial}{\partial t}\int_S \vec{B}\,d\vec{s}$


Или, что то же самое,

$2\pi r E_\varphi = -\frac{\partial}{\partial t}\Phi(r,z - v t)$


Здесь мы воспользовались аксиальной симметрией задачи по отношению к оси $z$, а также учли, что индуцированное электрическое поле имеет только азимутальную компоненту $\vec{E} = E_\varphi \vec{e}_\varphi$.
Отсюда можно найти азимутальную компоненту электрического поля, индуцированного магнитом.

$E_\varphi(r,z) = -\frac{1}{2\pi r}\frac{\partial}{\partial t}\Phi(r, z - v t)=-\frac{3\mu_0\,p_m}{4\pi}\frac{rv(z-v t)}{\left(r^2 + (z-v t)^2\right)^\frac{5}{2}}$


Теперь, когда у нас есть выражение для электрического поля, можно вспомнить и о трубе. Как показано на рисунке выше, внутренний радиус трубы равен $a$, а внешний — $b$. Материал трубы — медь. В данный момент нам будет нужна только электрическая проводимость меди. Обозначим проводимость за $\sigma$.
Электрическое поле внутри проводника вызывает электрический ток. Поэтому можем записать закон Ома в дифференциальной форме

$\vec{j} = \sigma \vec{E}$


Электрический ток, в свою очередь вызывает омические потери внутри проводника. Иными словами, энергия рассеивается внутри проводника и переходит в форму тепла, строго говоря, в нашем случае во всём объёме проводника.
Объёмная плотность мощности омических потерь по определению равна

$w = \vec{j}\cdot\vec{E} = \sigma E^2$


С другой стороны, при движении магнита сверху вниз потенциальная энергия магнита в поле тяжести Земли уменьшается, однако, скорость движения при этом остаётся постоянной, то есть не растёт, как это бывает при свободном падении. Это означает только одно: потенциальная энергия магнита рассеивается внутри проводника. А с точки зрения сил, действующих на магнит, на него действует сила трения, которая его тормозит и рассеивает потенциальную энергию магнита в тепло.
Запишем теперь баланс мощности в задаче: скорость убывания потенциальной энергии равна мощности омических потерь в проводнике.

$\frac{dE_p}{dt} = P$


$-mg\dot{z} = \int_V w\,dV$


$mgv = \int_{-\infty}^{\infty}\int_0^{2\pi}\int_a^b \sigma E^2\,r\,dr\,d\varphi\,dz$


Здесь необходимо заметить, что потенциальная энергия в координатах, изображенных на рисунке выше будет равна $E_p = - mgz$, а чтобы найти полную мощность омических потерь, следует проинтегрировать $w$ по всему объёму проводника. Длину трубы считаем бесконечной. Это не так далеко от истины, если учесть, что в опыте из видеоролика диаметр магнитика много меньше длины трубы.

Последний тройной интеграл выглядит очень сложным. И так оно и есть! Но, во-первых, интегрирование по азимутальному углу $\varphi$ можно заменить просто домножением на $2\pi$ в силу аксиальной симметрии задачи. Во-вторых, порядок интегрирования в данном конкретном интеграле можно изменить и сначала проинтегрировать по $z$, а уж потом по $r$. В-третьих, при интегрировании по $z$ по бесконечным пределам можно смело отбросить слагаемое $-vt$. Оставшийся интеграл берется машиной.

$\int_{-\infty}^\infty \frac{z^2\,dz}{\left(r^2 + z^2\right)^5} = \frac{5\pi}{128r^7}$


В итоге получается ответ для полной мощности омических потерь

$P = \frac{15}{1024}\,\mu_0^2\,p_m^2\,\sigma\left(\frac{1}{a^3} - \frac{1}{b^3}\right)v^2 = k\,v^2$


Здесь после второго знака равенства мы обозначили коэффициент трения

$k = \frac{15}{1024}\,\mu_0^2\,p_m^2\,\sigma\left(\frac{1}{a^3} - \frac{1}{b^3}\right)$


Отметим что, коэффициент трения $k$ зависит только от намагниченности магнита $p_m$, свойств материала проводника $\sigma$ и геометрических размеров трубы $a$ и $b$ — то есть зависит исключительно от параметров магнита и трубы и не зависит от, например, скорости или времени. Это хороший знак для нас и маленький зачётик в копилку найденных формул! Отсюда же становится понятно, почему для демонстрации опыта выбрана именно медная труба, а не, скажем, стальная. Трение зависит от проводимости линейно $\sigma$, а у стали проводимость меньше на порядок.

А что если труба сделана из сверхпроводника?
Это же обстоятельство объясняет и почему магнит левитирует над поверхностью сверхпроводника. Когда мы подносим постоянный магнит к сверхпроводнику, в последнем индуцируются незатухающие внутренние токи, которые создают своё магнитное поле и отталкивают магнитик.


Теперь можно записать

$mgv=kv^2\\mg = kv$


И внезапно (!), перед нами третий закон Ньютона! Сила действия равна силе противодействия. Можем найти установившуюся скорость движения магнита

$v_s = \frac{mg}{k}$



Уравнение движения


Настал черёд уравнения движения. С помощью второго закона Ньютона его будет записать очень просто

$ma=mg - kv\\ m\ddot{z} + k\dot{z} = mg$


Решать уравнение для $z(t)$ неинтересно, потому что ну просто координата меняется с постоянной скоростью. Гораздо полезнее знать, как быстро стабилизируется падение, чему равна установившаяся скорость падения. В общем, надо решать это уравнение для скорости

$\dot{v} + \frac{k}{m} v = g$


А решение будет такое

$v(t) = v_0\,e^{-\alpha t} + v_s\left(1 - e^{-\alpha t}\right)$


Здесь $\alpha = k/m$ — коэффициент затухания. Характерное время выхода на установившийся режим падения — $\tau = \alpha^{-1}$. Начальная скорость — $v_0$, установившаяся скорость — $v_s$.

А вообще, это уравнение парашютиста. Вот, наверное, почему статья Популярной Механики называется «Магнитный парашют».

Численный эксперимент


А теперь будет то, ради чего всё это затевалось. Навели тут, понимаешь, теорию. А на что она способна? Вдруг это всего лишь как тень на плетень? Или вообще не работает…

Для начала нужно разобраться с геометрией задачи. Видео у нас из MIT, стало быть, американское. Попробую угадать размеры их демонстрационной установки в дюймах (они же в дюймах любят всё измерять). Размер магнитика похож на $d = 1/2$ дюйма в диаметре. Это из тех какие есть в продаже. Тогда масса такого магнитика будет равна примерно $m = 8$ г. Размер медной трубы в длину похож на $l = 12$ дюймов (1 фут), а внутренний и внешний диаметры трубы, скорее всего, $2a = 3/4$ дюйма, $2b = 3/2$ дюйма.

С геометрией, вроде разобрались. Теперь физические свойства. Проводимость меди $59.5\times 10^6$ См/м.

Ранее здесь было написано, что я не смог увязать остаточную намагниченность неодимового магнита с его эквивалентным магнитным моментом. Но нашлись добрые люди в комментариях. Пользователь DenisHW любезно подсказал источник (см. п. 5 в списке литературы), где можно прочитать, помог сделать необходимые расчёты и даже проверил их на симуляторе FEMM.

Расчёт магнитного поля шарика из NdFeB на симуляторе FEMM
Расчёт магнитного поля шарика из NdFeB на симуляторе FEMM. Изображение предоставлено пользователем DenisHW

Итак, что удалось выяснить. NdFeB магнит относится к классу парамагнетиков, поскольку под воздействием внешнего поля, внутреннее поле усиливается. Более того, сплав NdFeB способен сохранять внутреннее поле после прекращения воздействия внешнего поля. Этот факт классифицирует NdFeB как ферромагнетик. Если обозначить индукцию внутреннего поля магнетика за $B$, а напряжённость внешнего магнитного поля за $H$, то выполняется равенство

$B = \mu \mu_0 H = (1 + \chi)\mu_0 H = \mu_0(H + I)$


Здесь $\chi$ — магнитная восприимчивость вещества, а $I$ — вектор намагниченности вещества.

Когда магнит изготавливают на фабрике, его замагничивают внешним полем $H$, а затем внешнее поле отключают, причём магнит сохраняет некоторую остаточную намагниченность $B_r$. Известно, что для неодимовых магнитов остаточная намагниченность равна примерно $B_r = 1\,..\,1.3$ Т. Теперь, если исключить внешнее поле $H$ из предыдущего уравнения, получится

$B_r = \mu_0I$


Откуда находим магнитный момент, приходящийся на единицу объёма материала $I$ как

$I = \frac{B_r}{\mu_0}$


Чтобы найти магнитный момент магнита в целом, нужно умножить $I$ на объём шарика $V$

$p_m=IV=I\cdot\frac{4}{3}\pi\left(\frac{d}{2}\right)^3$


Для остаточной намагниченности $B_r = 1$ Т получается $p_m = 0.853$ Ам?.
Ниже построен график $z$-компоненты магнитного поля в зависимости от радиальной координаты в нашей задаче на расстоянии половины диаметра шарика.

z-компонента магнитного поля на поверхности постоянного магнита
$z$-компонента магнитного поля рядом с поверхностью постоянного магнита

Когда-то доводилось измерять прибором. Поля прямо на поверхности таких магнитов обычно оказываются меньше остаточной намагниченности и составляют порядка нескольких тысяч гаусс. То, что я измерял для прямоугольного магнита, было около 4500 Гс. Поэтому у нас на графике магнитного поля получился вполне реалистичный результат.

Теперь воспользуемся решением уравнения движения, чтобы построить график скорости магнита. Для всех выбранных выше параметров коэффициент трения получается равным $k = 1.015$ Н/(м/с), установившаяся скорость — $v_s = 7.77$ см/с — как раз примерно 3 дюйма в секунду! На видео шарик проходит через трубу длиной в 12 дюймов примерно за 4 секунды.

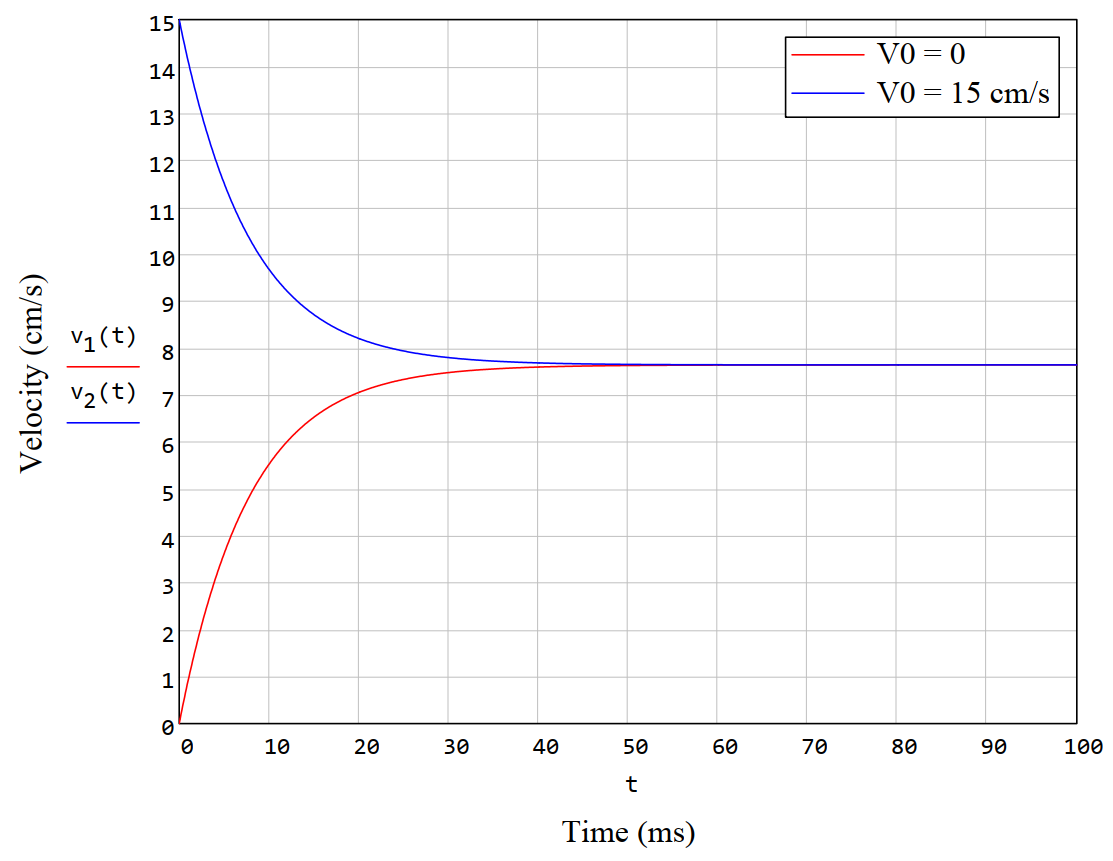
График решения уравнения движения магнитика в медной трубе
График решения уравнения движения магнитика в медной трубе

ЭТО ЗАЧОТ!
Знаю, что правильно «зачёт» писать через «ё», но в данном случае правильнее будет через «о» ;-)

А мы продолжаем. Рассеиваемая мощность оказывается равной примерно $P \approx 6$ мВт, а характерное время выхода на установившийся режим — $\tau \approx 8$ мс. Ниже построены графики $v(t)$ для двух разных начальных скоростей: нулевой, и $v_0 = 15$ см/с.

И вдобавок, пользователь vashu1 справедливо заметил, что неплохо бы было узнать ток, наведённый в медной трубке. Что ж, и это можно. Проинтегрируем

$J = \int_{0}^{\infty}\int_a^b \sigma E(r,z)\,dr\, dz = \frac{\sigma\, v\,\mu_0\, p_m}{4\pi}\left(\frac{1}{a} - \frac{1}{b}\right)$


Интегрировать по $z$ нужно именно по полубесконечным пределам, поскольку в другой половине трубы ток течёт в обратном направлении. У меня в ответе получилось $J = 20$ А. Честно говоря, я не ожидал, что получится такой большой ток. У пользователя vashu1 получилось 50 А, что, по-видимому, тоже недалеко от действительности. Думаю, vashu1 посчитал сумму токов во всей трубе, что из соображений мощности, тоже разумно.

Вот такое вот получилось исследование. Надеюсь, что было интересно. Оставляйте ваши комментарии. Постараюсь ответить всем. Если вам понравилась статья, поддержите автора лайком или плюсиком в карму. Спасибо, что прочитали.

Литература


  1. Джексон, Дж. Классическая электродинамика: Пер. с англ. Мир, 1965.
  2. Ландау, Л. Д., & Лифшиц, Е. М. (1941). Теория поля. Москва; Ленинград: Государственное издательство технико-теоретической литературы.
  3. Сивухин, Д. В. «Общий курс физики. Том 3. Электричество.» Москва, издательство “Наука”, главная редакция физико-математической литературы (1977).
  4. Яворский, Б. М., and А. А. Детлаф. «Справочник по физике.» (1990).
  5. Кириченко Н.А. Электричество и магнетизм. Учебное пособие. — М.: МФТИ, 2011. — 420 с.