Приветствую Вас! Сегодня хочу рассказать о геометрическом объекте, который похож на бумажный фонарик, но на самом деле является очень интересным контрпримером в области нахождения площади многогранников. Итак, поехали!
Парадокс лестницы
Архимед приближенно определял длину окружности с помощью длин сторон вписанных и описанных правильных многоугольников. В общем смысле, длину любой кривой можно выразить как наибольшее значение длин вписанных ломаных. Однако для корректной работы этого метода вершины ломаных должны находиться на самой кривой, а не просто рядом с ней.

В противоположном случае, как показано в так называемом "парадоксе лестницы", ломаные состоящие из вертикальных и горизонтальных отрезков общей длиной 2, могут быть расположены настолько близко к диагональному отрезку длиной √2, что они будут "визуально" сходиться к диагонали, но будут иметь разную длину.
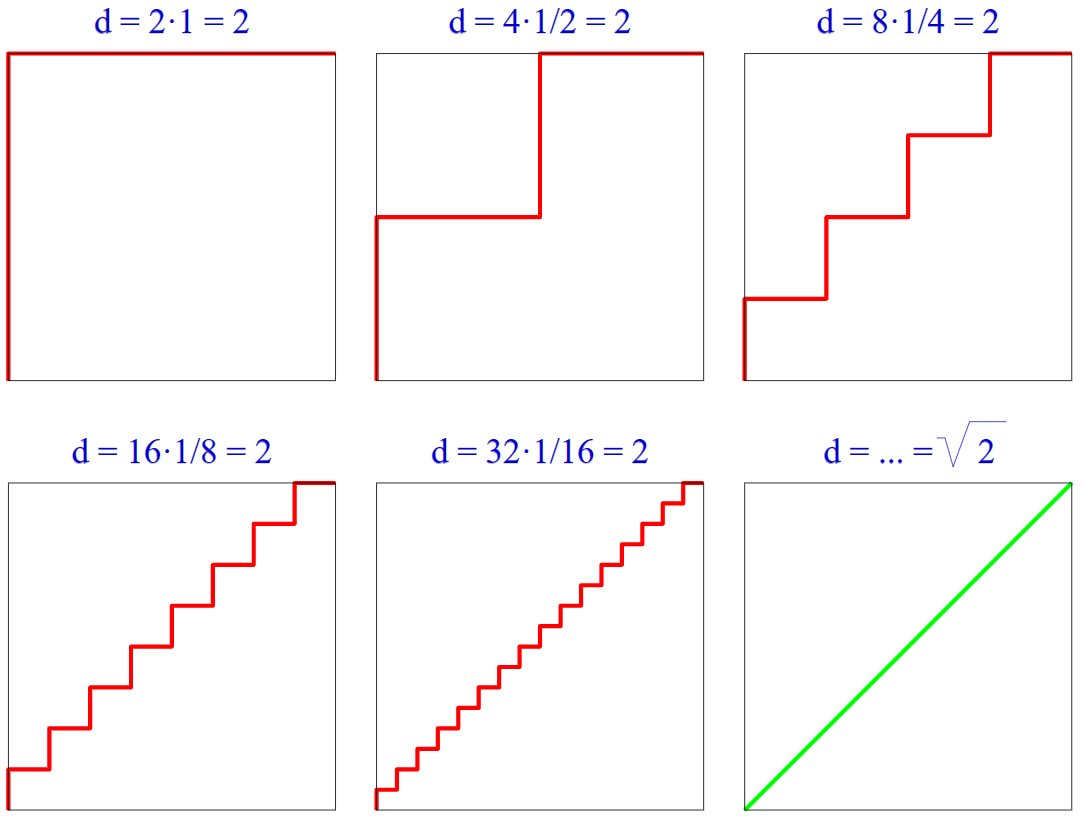
Сапог Шварца приводит аналогичный контрпример для площади поверхности, демонстрируя, что для точного приближения площади требуется еще больше, чем просто условие, что вершины лежат на искомой поверхности.

В конце XIX века немецкий математик Герман Шварц (1843-1921) разработал свою собственную конструкцию, которая послужила контрпримером к ошибочному определению, представленному в книге 1868 года Ж. А. Серре "Курс дифференциального исчисления и интеграла". В этой книге утверждалось, что:
Пусть часть криволинейной поверхности ограничена контуром C; мы определим площадь этой поверхности как предел, к которому S стремится площадь вписанной многогранной поверхности, образованной из треугольных граней и ограниченной многоугольным контуром Γ пределом которого является контур C. Необходимо показать, что предел S существует и что он не зависит от закона, согласно которому грани вписанной многогранной поверхности сжимаются.
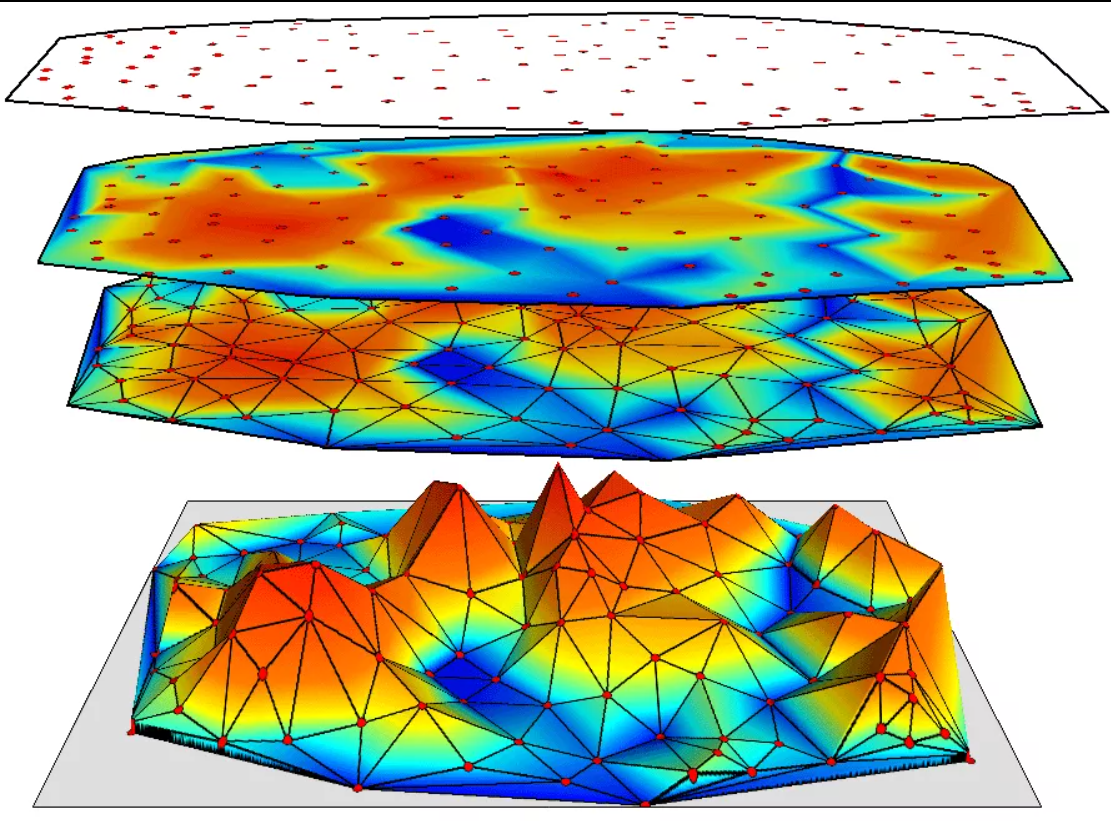
Конструкция сапога Шварца
Шварц разработал метод приближения поверхностей с помощью антипризм. Первый параметр антипризмы, обозначим его как "m", представляет собой количество кругов, второй параметр, обозначим его как "n", представляет половину числа треугольников в каждом кольце этой структуры. Для случая с одним кольцом (m=1) результирующая поверхность формируется из треугольных граней, составляющих антипризму порядка n.
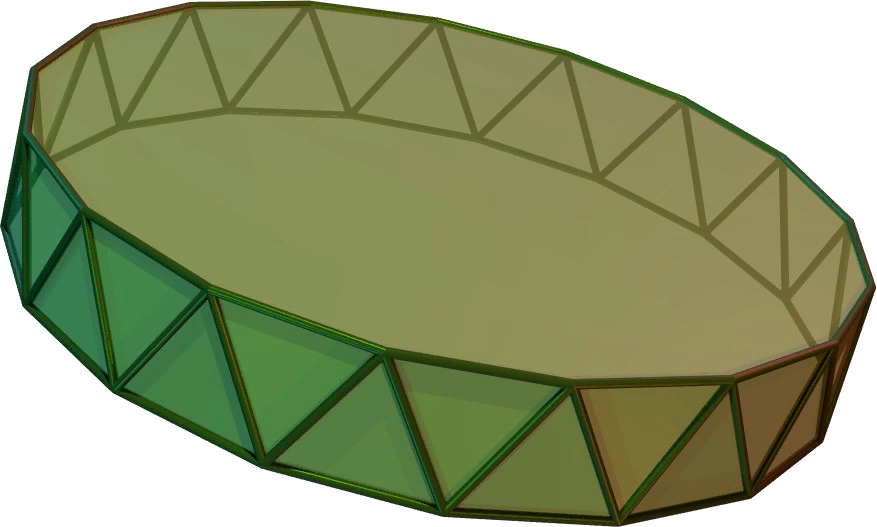
При более высоких значениях m, сапог Шварца формируется путем компоновки m таких антипризм.

Для построения сапога Шварца, который приближает заданный правильный круговой цилиндр, цилиндр разрезается на m блинов. Эти блины имеют m+1 круглых границ - две на концах цилиндра и еще одну на месте разреза. В каждом блине распределены n вершин, образуя правильный n-угольник (понятно, что количество этих углов можно увеличивать, стремясь ко сходству с окружностью).

Эти многоугольники повернуты на угол π/n от одной окружности к следующей, так что ребра правильных многоугольников и ближайшие вершины на следующем блине образуют основание и вершину равнобедренного треугольника. Эти треугольники пересекаются от края до края, образуя многогранную поверхность сапога Шварца, которая топологически эквивалентна цилиндру.
Сапог Шварца можно склеить из плоского листа бумаги с нанесенными на него гранями треугольников. Такой рисунок складок называется рисунком Йошимуры:

Если вывести формулу площади поверхности сапога Шварца, то получится следующее выражение:
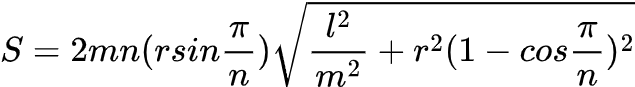
Парадокс
Если вычислить последовательно пределы, очевидно получится отличное приближение к площади поверхности цилиндра:
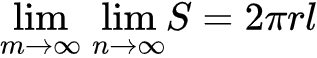
В этом случае внутренний предел уже сходится к нужному значению, а внешний предел является избыточным (иначе говоря, не важно, на сколько блинов будет разрезан цилиндр, вся апроксимация произойдет за счет большого числа треугольников).

В данном случае, при заданном значении n, с увеличением m и уменьшением длины каждой цилиндрической полосы l/m, каждая из соответствующих полос из равнобедренных треугольников становится практически плоской. Площадь поверхности каждого блина стремится к конечному числу, а так как во втором пределе мы неограниченно увеличиваем количество блинов, то общая площадь поверхности стремится к бесконечности.
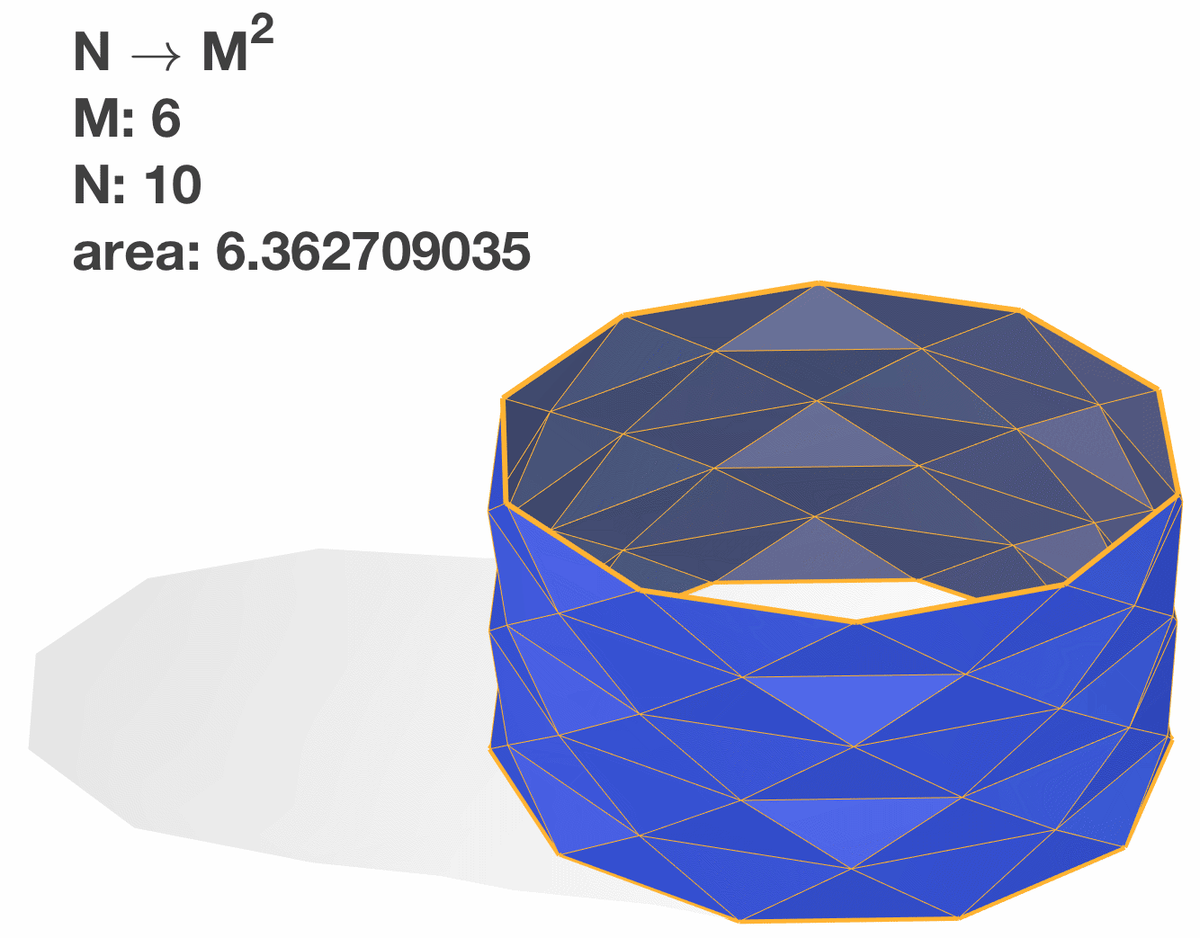
Также можно установить функциональную связь между параметрами "m" и "n" и исследовать предел при одновременном увеличении обоих параметров с сохранением этой связи.
Различные варианты такой связи могут привести к двум возможным сценариям: сходимости в определенной области или расходимости до бесконечности. Например, если выбрать m = cn (где c - произвольная константа) и рассматривать предел для больших значений n, то произойдет сходимость в определенной области. В то время как установка m = cn³ приведет к расходимости. Третий тип ограниченного поведения достигается при m = cn². Для данного выбора параметров, получим формулу:
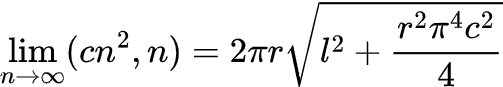
Играя значением c, можно получить любое значение площади поверхности. Показанное выше также подчеркивает важность тщательного выбора способа разбиения на треугольники для использования в компьютерной графике и методе конечных элементов, применяемом в научном и инженерном моделировании. В области компьютерной графики сцены часто представляются в виде треугольных поверхностей, и правильное отображение освещения зависит от ориентации нормалей к поверхности.
Все объемные выкладки - в одной статье.
Неправильный выбор способа разбиения на треугольники, подобно тому, как это происходит в случае с сапогом Шварца, может привести к образованию поверхности, наподобие складной гармошки, с нормалями, которые далеки от нормалей исходной поверхности. Близко расположенные резкие изгибы на этой поверхности также могут вызвать проблемы при сглаживании.
Проблемы возникают, когда в разбиение включены треугольники с углами, близкими к 180 градусам. В некоторых классах сапогов Шварца, которые используют углы ограниченные 180 градусами, площадь сходится к той же площади, что и у цилиндра, по мере увеличения числа треугольников до бесконечности.

Метод конечных элементов, в своей базовой форме, приближает гладкую функцию (часто представляющую решение задачи физического моделирования в науке или инженерии) путем замены её кусочно-линейной функцией на триангуляции. Пример с сапогом Шварца демонстрирует, что даже для простых функций, таких как высота цилиндра над плоскостью, проходящей через его ось, и даже если значения функции точно известны в вершинах триангуляции, использование триангуляции с углами, близкими к 180 градусам, может привести к значительно неточным результатам моделирования.
Больше математики в Telegram - "Математика не для всех".
Комментарии (14)

Aquahawk
20.08.2023 08:46+1Шикарно. Мне нравится смотреть как становилась математика и как допускались ошибки. Шикарный пример также с гипотезой Ампера, что всякая «произвольная» функция дифференцируема всюду, за исключением «исключительных и изолированных» значений аргумента. Сейчас это называется гипотеза. Я очень хотел понять, как формулировал сам Ампер когда это публиковал. Есть оригинал публикации Ампера 1806 года http://www.ampere.cnrs.fr/bibliographies/pdf/1806-P005.pdf но он на французском. И я не нашёл старых переводов ни на русский ни на английский. В 1861 Риман высказал сомнения, без четкого доказательства, и тольо 1872 году Вейерштрасс предъявил миру такую всюду недифферинциремую функцию. Сейчас все пишут исходя из того, что Ампер в своей гипотезе не прав, а что писали тогда, с 1806 по 1861, считалось ли это тогда истиной или гипотезой? Я не смог найти внятных публикаций про это именно тех времён.

avost
20.08.2023 08:46+1считалось ли это тогда истиной или гипотезой?
Это же математика. Пока теорема не доказана она не может считаться истиной даже потому, что её сформулировао Ампер.

Aquahawk
20.08.2023 08:46+1так это сейчас сказали что она тогда была не доказана. Есть мнение что Ампер не высказывал гипотезу, а доказывал своё утверждение. Для этого нужно найти перевод на английский или русский язык выполненный до 1861 года. Тогда мы сможем понять что имел ввиду Ампер и как это тогда воспринимали, как доказательство или как гипотезу.

avost
20.08.2023 08:46Есть мнение что Ампер не высказывал гипотезу, а доказывал своё утверждение
Тогда это тоже не истина, а теорема. Да, доказательство могло быть ошибочным, но вероятность этого не особо велика.

Aquahawk
20.08.2023 08:46+4Вот учебник Франкера 1840 года, перевод с Французского 4го издания, выдержки




Единственную оговорку я нашёл
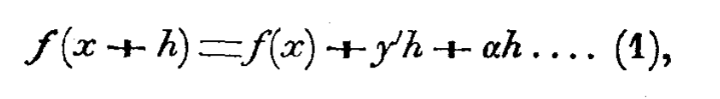

Что имхо говорит что может и есть отдельные точки где производной нет, но в остальных иксах производная есть, для любой функции. И мне кажется что до того, как Риман в 1861 усомнился в дифференцируемости любой функции, существование производной было научным консенсусом и считалось либо доказанным, либо не требующим доказательства утверждением. Именно поэтому я хочу прочитать как писал сам Ампер.
Учебник, если что тут:
https://cat.gpntb.ru/?id=FT/ShowFT&sid=00a813070c1835d8252a61404b30663b&page=443&squery=
На мой взгляд там явно утверждается существование производной для любой функции

Aquahawk
20.08.2023 08:46Коши, в переводе Буняковского, 1831 год. Не требует ничего, кроме непрерывности для существования производной.


Portnov
20.08.2023 08:46+1Математика в 19м веке была несколько не та, что в 20м. Классические теоремы дифференциального исчисления (Ролля, Лагранжа, вот это всё) в оригинале начинались со слов "пусть есть непрерывная функция", а доказательство строилось так, как будто функция дифференцируемая. Что началось после публикации контрпримера Вейерштрасса... :)

GospodinKolhoznik
20.08.2023 08:46+4Так оно и сейчас продолжается, просто в какой то момент уже забили и зафиксировали ВУЗовский матан в том состоянии, в котором он был на начало XX века. В XVIII веке всем было пофиг на аксиоматику, доказывалась всё на пальцах, потом решили, что это какой то позор, и раз уж древние греки смогли геометрию аксиоматизировать, то чем мы хуже, и Лагранж с Коши и компанией придумали матан с его определениями и теоремами. В XIX веке писали "функция непрерывная" потом после Вейерштрасса стали писать "функция непрерывная и дифференцируемая сколько угодно раз", большинство теорем пришлось переработать, а потом математики понаоткрывали новые контрпримеры, но все дружно сказали "Довольно!" и не стали переписывать учебники для ВУЗов, ибо те и так уже стали перегружены формализмом, за которым уже трудно уловить суть теоремы. Ну т.е. матан продолжает развиваться, но только в научных статьях, а в учебники эти новые открытия уже не попадают, из педагогических целей, чтобы студенты совсем не офигели и хоть что то поняли.

Aquahawk
20.08.2023 08:46Да ладно, всё там есть, везде эта дифференцируемость требуется и каждый раз когда что-то решаешь её надо отдельно доказывать. Во всяком случае на ВМК надо.

ermouth
20.08.2023 08:46+1Скульптор Noah Deledda сапоги Шварца из пивных банок делает, оч красивые скульптуры:


rybkin_kotik
20.08.2023 08:46У Фихтенгольца, что ли, я этот пример видел... Вот что он называется "сапогом Шварца", не знал.









rebuilder
А если не использовать углы близкие к 180 градусам? Для своей работы использую триангуляцию Делоне, как понимаю она позволяет избегать острые углы.
Un_ka
При триангуляции объёмов или плоскостей помимо углов, можно использовать параметр соотношение сторон: для треугольника это соотношение площадей треугольника к площади равностороннего треугольника вписанного в окружность в которую вписан оцениваемый треугольник. В идеале 1. Если он будет сильно близок к нулю, при решении каких либо задач в пакетах численного моделирования могут быть проблемы.