26.02.2021 08:02
BiZone_team 6 1200 Источник

Автор: Иннокентий Сенновский (rumata888)


Хочу поделиться опытом регистрации уязвимостей в продуктах компаний без Bug Bounty. У меня этот процесс занял целых два года, в течение которых я общался с вендорами, боролся с недопониманием и стучался в MITRE.


Проблемы мотивации и целесообразности поиска уязвимостей в таких продуктах оставим за рамками этой статьи. Обсудим, что делать, если баг уже обнаружен. Если вам не терпится сразу почитать советы, переходите к последней части.



Photo credit: https://www.deviantart.com/heroeswho


Незапланированный багхантинг, или С чего все началось


В 2018 году мы с командой придумали для CTF-таска плату с двумя чипами: один — с базовой логикой, другой — для аутентификации. Предполагалось, что при успешной эксплуатации встроенных уязвимостей атакующие смогут загрузить свой вредоносный код в память чипа с логикой, но взломать чип аутентификации не смогут.


У атакующей команды не было возможности клонировать устройство и в дальнейшем эмулировать его. Чтобы получить флаг в каждом раунде, ей предстояло взаимодействовать с чипом аутентификации на целевом устройстве. Обычно такие механизмы требуют криптографических решений.


Поскольку мы планировали использовать чипы STM для обоих микроконтроллеров, я обрадовался (как оказалось, преждевременно), когда узнал что компания ST предоставляет предкомпилированные криптографические библиотеки для своих устройств под названием STM32 cryptographic firmware library software expansion for STM32Cube (X-CUBE-CRYPTOLIB). Я решил изучить их и наткнулся на одну штуку в разделе RSA, которая меня насторожила: в библиотеке прошивок были 4 экспортированных функции, представленные в таблице ниже.


Название функции Описание
RSA_PKCS1v15_Sign PKCS#1v1.5 RSA Signature Generation Function — функция генерации подписи
RSA_PKCS1v15_Verify PKCS#1v1.5 RSA Signature Verification Function — функция проверки подписи
RSA_PKCS1v15_Encrypt PKCS#1v1.5 RSA Encryption Function — функция шифрования
RSA_PKCS1v15_Decrypt PKCS#1v1.5 RSA Decryption Function — функция расшифровки

К 2018 году спецификация PKCS#1v1.5 должна была кануть в прошлое из-за критической уязвимости, но теперь выяснилось, что старая версия с багом все еще применяется.


Вот почему нельзя использовать PKCS#1v1.5.

PKCS#1v1.5


PKCS#1 — криптографический стандарт (спецификация) для алгоритма RSA. Он определяет примитивы и схемы применения RSA для шифрования и подписи с помощью открытого ключа. Текущая версия стандарта — 2.2, однако в библиотеке X-CUBE-CRYPTOLIB используется версия 1.5. В ней и обнаружена критическая уязвимость, которая возникает в процессе шифрования и расшифровки.


Базовый RSA


В основе примитива RSA лежит вычислительная сложность задачи факторизации произведения двух больших простых чисел. Представим, что Боб собирается отправить Алисе сообщение, которое, как предполагается, прочитать сможет только она. Они выбирают следующий алгоритм:


  • Алиса произвольно выбирает два простых числа (p и q) заданной длины (например, 1024 бита).
  • Алиса вычисляет результат их умножения — N (модуль).
  • Алиса берет заданное открытое значение степени e. Как правило, это 65537, потому что в двоичном представлении этого числа ненулевыми являются только два бита. Раньше также использовались 3 и 17, но при возведении в степень превышение модуля не гарантировалось.
  • Алиса вычисляет закрытую экспоненту d. Теперь у нее есть закрытый (d, N) и открытый ключи (e, N).
  • Алиса направляет свой открытый ключ Бобу.
  • Боб конвертирует сообщение M, которое он собирается отправить Алисе, в число m, которое меньше N. Он возводит число в степень e по модулю N и отправляет сообщение Алисе.
  • Алиса принимает результат и возводит его в степень d по модулю N и в итоге получает исходное число m, которое конвертирует обратно в M.

$N = p ? q$, где p, q — простые числа
$inline$e ? d=1 (mod (p ? 1)?(q ? 1))$inline$
$inline$?m?0,a*p,b*q : m^{e?d} (mod N)=m^{1+k?(p?1)?(q?1)} (mod N) = m (mod N)$inline$, где $k,a,b?\mathbb{N}$


Проблемные места RSA


Для вычисления модуля нельзя просто выбрать любые два простых числа — они должны соответствовать определенным требованиям, иначе примитив становится небезопасным. Но даже если выбраны идеально подходящие p и q, остаются другие проблемы.


Далее по тексту m — открытый текст (сообщение), а c — закрытый текст.


Вот что будет, если вместо 65537 в качестве открытого значения степени выбрать меньшее значение, например, 3.


Если p и q равны 1024 битам, то модуль будет состоять из 2048 битов или 256 байтов.


Если сообщения, которые Боб собирается отправить Алисе, меньше или равны $\left[\frac{256}{3}\right]=85$, то результат возведения в степень не превысит значение модуля. В таком случае дешифровать текст будет несложно: достаточно извлечь корень третьей степени.


Если Боб повторно отправляет сообщения, то они шифруются одинаково, поэтому при реализации MitM-атаки злоумышленник может частично извлечь информацию о них: в определенные моменты времени Боб отправляет одинаковые сообщения.


Спецификация PKCS#1v1.5


Для решения этих проблем в компании RSA разработали спецификацию PKCS#1 v1.5 (Public Key Cryptography Standards — «Стандарт криптографии с открытым ключом»). Она предусматривает форматирование для шифруемых и подписываемых блоков при помощи специального дополнения — padding. Дополнение применяется перед тем, как блок будет полностью зашифрован.
Предположим, длина модуля N в октетах (байтах) равна k. Данные для шифрования/подписи — D. Получается следующий блок:


EB = 00 || BT || PS || 00 || D,


где BT равно 00 или 01 для операций с закрытым ключом (подписи) и 02 для операций с открытым ключом шифрования.
Блок переводится в целое число при помощи конвертации big-endian (первый октет EB наиболее значимый).
PS состоит из октетов k-3-len(D). Его содержимое зависит от BT:


  • если BT равно 00, все октеты в PS становятся равными 00;
  • если BT равно 01, все октеты в PS становятся равными FF;
  • если BT равно 02, все октеты в PS генерируются псевдослучайно и не равны 00.

Рекомендуется использовать BT=01 для подписей и BT=02 для шифрования, поэтому:


  1. при BT, равном 01, можно снять дополнение с D независимо от его содержания;
  2. при BT, равном 00, с первого байта данных D, равного 00, также будет снято дополнение, что создает проблему;
  3. BT, равный 01, и BT, равный 02, порождают большие целые числа для шифрования, поэтому все атаки, для которых требуется небольшое значение открытого текста, не работают.

Также можно заметить, что первый октет EB равен 00. Данное значение было выбрано так, чтобы целое число, которое получается в результате EB, всегда было меньше модуля N.


На первый взгляд эта схема кажется вполне надежной и решает перечисленные выше проблемы. Но если бы все было так здорово, то я бы не писал эту статью.


Атака Блейхенбахера Padding Oracle


Атаке, о которой пойдет речь, уже 22 года.


Чтобы разобраться в ней, вернемся к Алисе и представим, будто она уже создала пару ключей и отправила открытый ключ Бобу, но теперь оба используют дополнение из PKCS#1v1.5 в своих зашифрованных сообщениях. Вот что происходит, когда зашифрованный текст отправляется Алисе:


  • Алиса расшифровывает текст при помощи примитива RSA;
  • Алиса снимает дополнение с сообщения;
  • Алиса анализирует сообщение и выполняет действия в соответствии с его содержимым.

Обычно в случае проблемы с получением команд различные программы и системы (Алиса в нашем примере) сигнализируют отправителю (Бобу), что что-то пошло не так. Такие сигналы часто точно показывают, где возникла проблема: на втором этапе (неверное дополнение) или на третьем (что-то не так с самой командой). Распознать второй и третий этапы, как правило, можно только при помощи закрытого ключа. Поэтому, когда Алиса сообщает, что снятие дополнения прошло успешно или неуспешно, она фактически раскрывает информацию об открытом тексте.


В качестве мысленного эксперимента давайте посмотрим, что будет, если отправить произвольное целое число на расшифровку вместо обычного сообщения. Какова вероятность, что при снятии дополнения не возникнет ошибка? Первые два октета EB должны быть представлены как 00 || 02, остальные октеты — иметь как минимум одно значение 00. Если k равно 256, тогда


$P=\left(\frac{1}{256^2}\right).\left(1-\left(\frac{255}{256}\right)\frac{254}{}\right)\approx\frac{1}{104031}$


Вероятность кажется слишком низкой, но на самом деле она достаточно высока, чтобы атакующий мог этим воспользоваться. В атаке применяется гомоморфизм RSA относительно умножения:


$?x : (x?m)^e (mod N)=x^e ? m^e (mod N)$


Вот как развивается атака. Мы выбираем c, для которого хотим найти


$m=c^d mod N$


Для удобства в дальнейшем пояснении будем использовать следующие константы:


$B = 2^{8(k?2)}, k = ||N||$


Если простой текст, который получается в результате расшифровки, соответствует спецификации PKCS, то ей соответствует и зашифрованный текст.


Мы выбираем целые числа s, вычисляем


$c' = cs^e mod N$


и направляем их в оракул (Алисе). Если $c'$ проходит проверку на ошибки, тогда


$2B ? ms mod N < 3B.$


Получив необходимое количество разных значений s, мы можем найти m. Обычно для этого требуется около 220 зашифрованных текстов, но их количество сильно разнится.


Можно выделить три стадии атаки:


  1. Ослепление зашифрованного текста, создание $с_0$, которое соответствует неизвестной величине $m_0$.
  2. Вычисление небольшого значения $s_i$?, чтобы $m_0s_i mod N$ отвечало требованиям PKCS. Для каждого такого $s_i$ атакующий, используя известную информацию, вычисляет интервалы, которые должны содержать $m_0$.
  3. Постепенное увеличение значения $s_i$, сужающее возможный диапазон $m_0$ до тех пор, пока не останется только одно возможное значение.
    Этот этап начинается, когда остается только один интервал. У атакующего имеется достаточно информации об $m_0$, чтобы выбрать такое $s_i$?, при котором вероятность соответствия $m_0s_i mod N$ спецификации PKCS выше, чем у произвольно выбранного сообщения. При достаточно небольшом интервале эффективнее подобрать значения локально, чем продолжать отправку запросов в оракул.

Итак, модель атаки будет следующая:


  • перехват сообщения Боба Алисе;
  • использование Алисы в качестве padding-оракула для расшифровки сообщения.

Обнаружив такую уязвимость в библиотеке программного обеспечения для микроконтроллеров, я решил проверить, нет ли ее в других библиотеках. Выяснилось, что Microchip также предоставляет библиотеку криптографических примитивов и, кто бы мог подумать, единственная схема шифрования для RSA — PKCS#1v1.5. Вот фрагмент функции расшифровки RSA:


// Find the message length
endPtr = (uint8_t *)tmpPtr->startAddress + rsaDesc0.cT.bLength - 1;

if ((*endPtr-- == 0x00) && (*endPtr-- == 0x02))
{
    while ((endPtr >= (uint8_t *)tmpPtr->startAddress) && (*endPtr-- != 0x00));

    if ((endPtr - (uint8_t *)tmpPtr->startAddress + 1) > rsaDesc0.cT.bLength - 11)
    {
        rsaDesc0.status = RSA_SW_STATUS_ERROR;
    }
    else
    {
        *msgLen = endPtr - (uint8_t *)tmpPtr->startAddress + 1;

        if (endPtr >= (uint8_t *)tmpPtr->startAddress)
        {
            uint8_t i = 0;

            while (endPtr >= (uint8_t *)tmpPtr->startAddress)
            {
                *(plainText + i++) = *endPtr--;
            }
        }
    }
}
else
{
    rsaDesc0.status = RSA_SW_STATUS_ERROR;
}

Байты памяти идут в обратном порядке, поэтому мы видим, что открытый текст оканчивается на 0200 вместо проверки наличия 0002 в начале. Если дополнение неверное, функция возвращает другой статус, что и делает ее опасной.


Время постучаться к производителям


В сентябре 2018 года я отправил описание уязвимостей в ST и Microchip, и вот к чему это привело.


Представители ST сначала активно отвечали на мои письма, но в процессе общения у нас возникло недопонимание. В этом отчасти была моя вина: я указал, что ошибка была в STM32-CRYP-LIB (это еще одна криптографическая библиотека ST) вместо X-CUBE-CRYPTOLIB. Дело в том, что STM32-CRYP-LIB не содержит примитивов шифрования и расшифровки для RSA, только примитивы подписывания или проверки.


Мое обоснование угрозы атаки Блейхенбахера Padding Oracle из-за бага вызвало сопротивление, поскольку это не всегда означает, что конечный продукт уязвим. Однако команда из ST согласилась, что при использовании версии PKCS#1v1.5 устранить проблему сложно. В октябре 2018 года мне сообщили, что началась разработка PKCS#1v2.2. Я подчеркнул, что все равно необходимо оповестить пользователей об уязвимостях.


В декабре 2018 года мне пришел ответ, основное содержание которого сводится к двум пунктам:


  • ST не хотела регистрировать уязвимость в базе CVE, так как производители следовали спецификации, а сама библиотека не выдавала ошибок дополнения (это так лишь отчасти);
  • началась разработка PKCS#1v2.2 — новой версии спецификации с более безопасным дополнением, релиз которой был запланирован на весну вместе с обновленной библиотекой X-CUBE-CRYPTOLIB.

Итак, попытки убедить ST зарегистрировать уязвимость в CVE так и не увенчались успехом.


Отчет в Microchip я отправил в сентябре 2018 года. Команда разработчиков откликнулась только в марте 2019 года, предложив решение проблемы: они посоветовали использовать Microchip Harmony, фреймворк для разработки ПО для встраиваемых устройств, вместо пакета MLA. Это действительно должно было сработать, так как Harmony содержит более современные спецификации, которые можно использовать вместо уязвимой. Тем не менее пользователям все еще нужно было сообщить об опасности применения RSA в MLA. Но поскольку на мой первый запрос Microchip отвечала полгода, я решил больше ничего не ждать, а искать другие пути.


Еще пара попыток получить CVE


Обращаться напрямую в MITRE можно только после того, как другие попытки не принесли результата, поэтому я решил попробовать присоединиться к The Internet — программе HackerOne. Для этого нужно обнаружить уязвимость в популярном проекте с открытым кодом или уязвимость, которая бы затрагивала множество поставщиков, а это как раз мой случай. Осталось только предоставить Proof-of-Concept (PoC).


Вот несколько технических особенностей, которые я выявил в начале работы над PoC.

Учитывая, что эти библиотеки предназначены для встраиваемых устройств, их использование на стандартных компьютерах с архитектурой AMD64 сопровождается некоторыми ограничениями.


Библиотека MLA распространяется в виде исходного кода, но как таковые bigint-вычисления реализованы в ассемблере архитектуры PIC. Мне пришлось переписать их в архитектуру AMD64.
Это заняло много времени, потому что ключевые вычисления были заточены под 16-битную архитектуру. Это сильно замедляет RSA, несмотря на нативное исполнение. Проведение атаки может занять несколько дней. На встраиваемом устройстве намного быстрее.


X-CUBE-CRYPTOLIB распространяется в скомпилированном формате. Чтобы использовать ее на обычном компьютере, мне пришлось эмулировать прошивку с помощью QEMU, что крайне негативно сказывается на быстродействии. Вдобавок ко всему, единственный подходящий интерфейс для передачи данных — это мучительно медленный, эмулированный UART (передача 256 байтов занимает 2 минуты). Чтобы решить проблему с интерфейсом, я установил отладочную ловушку, которая передает данные в память и в обратном направлении. По крайней мере так можно избежать проблем, связанных с эмуляцией передачи.


Однако даже в таких условиях реализация атаки проходит очень медленно. Поэтому, чтобы сэкономить время тестировщика, я написал две версии атаки для каждой из платформ:


  • полный цикл атаки (на библиотеку MLA займет много времени, на ST — нереально много времени);
  • атака с заранее просчитанными успешными шагами.

Во втором варианте алгоритм выполняется заранее при помощи python-сервера, который производит те же проверки, что и уязвимая библиотека. Он сохраняет все шаги, которые обеспечивают успешное снятие паддинга и позволяют сузить область открытого текста. Соответственно, атакующий применяет только эти шаги к уязвимой реализации, избегая мучительного перебора.


Также следует отметить, что библиотека X-CUBE-CRYPTOLIB защищена от использования на иных устройствах, кроме как ST (проверка выполняется путем записи и чтения битов из специальных регистров памяти). Они представлены на рисунке ниже (доступы к MEMORY). QEMU не проходит проверку, благо вместо отказа в расшифровке или шифровании данных процессы просто маскируют данные во время шифрования и возвращают больше данных (включая некоторые из произвольного дополнения). Маскировку можно откатить назад, если простой текст содержит только символы ASCII-7, так как все они меньше 128. Поэтому для использования библиотеки при помощи QEMU пришлось реализовать функцию снятия маскировки.



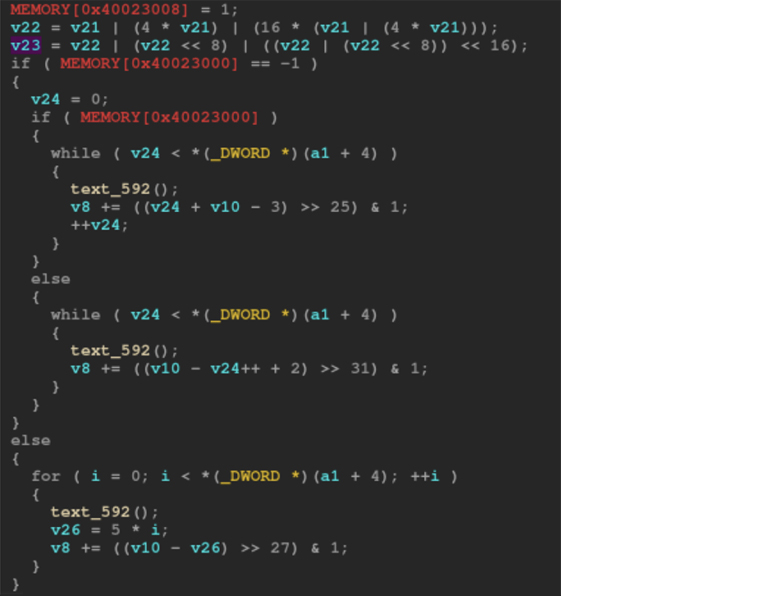
В библиотеке MLA было сделано только одно изменение: реализация bigint для арифметических операций в ассемблере Intel вместо PIC.


Изменения в библиотеку ST не вносились.


Если вас интересует полная версия PoС, переходите на GitHub.


Итак, в октябре 2019 года я подготовил и отправил PoC компании HackerOne. Но и здесь ничего не получилось: найденные мной баги не прошли по уровню критичности. Увы.


К тому моменту я перепробовал все и мог с чистой совестью обращаться в MITRE. 21 октября я написал им и получил в ответ отбивку. Спустя несколько дней спросил, требуется ли дополнительная информация, но никто так и не ответил.


В итоге я погрузился в работу и совсем забыл об этом письме.


Счастливый конец


В декабре 2019 года представители ST вернулись ко мне с новостями: они запланировали публикацию новой версии библиотеки со спецификацией PKCS#1v2.2 на начало 2020 года, а также обновление руководства пользователя X-CUBE-CRYPTOLIB, в котором будет предупреждение об уязвимости.


Библиотека по сей день не обновлена, но предупреждение появилось (см. рис. 1).



Рис. 1. Скрин из документации


Позже, уже в октябре 2020 года мне напомнили об этих уязвимостях. Я отправил еще один запрос в MITRE, но ответа не получил. Решил не сдаваться, спустя две недели повторил попытки и… Опять тишина.


Тут я осознал, что с момента первого письма в MITRE прошел уже год. В такой ситуации есть только одно эффективное решение — негодование в Twitter.



Рис. 2. Тот самый твит


Сработало!


Сразу после упоминания в твите MITRE зарезервировала номера в базе CVE и ответила на все мои старые письма.


Уязвимости зарегистрированы:


  • CVE-2020-20949 — уязвимость в библиотеке ST: X-CUBE-CRYPTOLIB 3.1.0, 3.1.2);
  • CVE-2020-20950 — уязвимость в библиотеке Microchip Libraries for Applications 2018-11-26).

Ура.


5 шагов к регистрации уязвимости в продуктах компаний без Bug Bounty


Вот что я бы посоветовал тем, кто нашел уязвимость в продукте компании без программы Bug Bounty и security.txt:


  • Оцените, стоит ли регистрация и устранение бага сил, которые вы потратите на PoC. Короче, точно ли оно вам надо?))
  • Если баг не дает покоя и вы решили, что оно вам все-таки надо, напишите вендору. Не забудьте указать сроки, в течение которых вы ждете ответа и устранения уязвимости. Рекомендую дать две недели на ответ на первое письмо. Стандартное время на устранение бага — 90 дней. Учитывайте, что иногда компании по объективным причинам нужно больше времени, чем вы требуете. В таком случае лучше уступить и договориться об отсрочке.
  • Если компания вас игнорирует или не считает проблему уязвимостью, определите, сколько времени вы готовы потратить на борьбу за справедливость работу с сопротивлением. Когда оно истечет, бегите в MITRE.
  • Если MITRE игнорирует вас в течение двух недель (пришла только отбивка, номера CVE так и не выделены), то пишите в Twitter с отметкой @CVENew.
  • Когда номера в CVE выделены, пишите статью и отправляйте ее MITRE и вендору.