«Скрытый код» принятых решений / forpes.ru

24.04.2022 14:05

S_A 0 1400 Источник

Есть способные к обучению объекты, как живые, так и некоторые математические конструкции. Обучение можно формулировать по-разному, но будучи обученным - что происходит при принятии решения? Некоторое соображение по этому поводу приведено в этой (нет, не научной) статье, не претендующей на какие-то откровения, а скорее на размышления.

Немного [философских] предпосылок

В этом тексте не будет употребляться слово "интеллект" (кроме этого раза), так как гуманитарии уже несколько тысяч лет не могут справиться с его определением, а математики похоже за определение еще как следует не брались.

А так, поскольку в обучении нейросетей подход следующий:

Составление прогноза (прямой проход), для обученный сети это вывод (inference),
Сравнение (вычисление функции потерь и её градиента),
Собственно обучение (обновление весов в обратную сторону от градиента),

Пошла философия

С другой стороны, вспоминая некоторые труды Карла Поппера, и живое обучается подобным образом (пробами и ошибками, но человек может исправлять свои ошибки на бумаге, благодаря естественному языку). Эволюция языка согласно ему - двигатель эволюции и человечества.

само принятие решения - это эксплуатация приобретенного в процессе материала.

Будучи "несколько обученным", некоторый "принимающий решение" алгоритм или человек, действует (исходя из того что имеет) прямым проходом. Однако любое решение принимается с какой-то целью, и его можно попробовать специфицировать в достигаемых решением результатах.

Запредельная философия

В конечном итоге, цель принятия решения живым или социальным - улучшить свое положение в среде. Говорят еще - противостоять хаосу, что-то около уменьшать энтропию (увеличивать вероятность нужных событий).

И эволюция материи направлена на усложнение форм переработки энергии - от ядерных процессов и гравитационных, химических, биологических, социальных, и далее информационных.

Поэтому хорошее новое положение дел или нет - должно определяться каким-то образом через информацию, или, математически, через статистику над событиями.

Получается, принятие решения - это попытка улучшить своё положение. Улучшается оно или нет - вот вопрос.

К определению "скрытого кода"

Раз уж есть тезис Чёрча, о том что интуитивно вычислимые алгоритмы (и в физической формулировке - физически вычислимые) реализуемы на машине Тьюринга, то можно заподозрить что за каждым принятым решением может стоять своя "программа".

Какова структура этой программы? Развернем, на минуточку, ситуацию в противоположную сторону, и представим что у нас не мозг моделируется нейросетью, а нейросеть - модель мозга. Вооружимся примитивной рекуррентной (так как она эквивалент машины Тьюринга) нейросетью, как ниже в коде.

class RNN(nn.Module):
    def __init__(self, outputs=1, channels=1, dropout=0.2):
        super(RNN, self).__init__()
        self.gru = nn.GRU(
            input_size=channels,
            hidden_size=128,
            dropout=dropout,
            batch_first=True
        )
        self.drop = nn.Dropout(dropout)
        self.output = nn.Linear(128, outputs)

    def forward(self, X):
        X = self.gru(X)[0][:, -1]
        X = self.drop(X)
        X = self.output(X)
        return X

В данном случае, основное в ней по отношению ко всему остальному - это dropout (зануление случайной части вычислений в прямом проходе). Известно, что если его на выводе потом не отключать, то можно сгенерировать разбросанные прогнозы.

Вот ниже приведена работа этой нейросети над моделируемой функцией:

$\sin^2(x)+\frac {cos(x)} {2} + \epsilon, \epsilon \sim N(0, 0.1)$

Слева - распределение известных и прогноза, справа - визуализация

Четкого доказательства нет, но усреднение этих разбросанных прогнозов даёт сам прогноз.

Слева сравнение известного и прогноза, справа - прогноза и усреднения после dropout на выводе

То есть можно представить, что есть некоторый "сюжет" из "элементарных деталей", а далее некоторое правило "фильтрует" его в результат (почти как оператор select в SQL).

Далее всё пойдет для дискретного случая, ибо на непрерывный сходу не обобщить.

Пока всё еще вязнет в абстракциях, но если определить что хорошие исходы принятого решения соседствуют с нехорошими, то для измерения изменения ситуации можно воспользоваться некоторым подобием энтропии Шеннона. Принятое решение должно учитывать ситуации как "до" и "после", и может быть взвешенной суммой разниц:

$C = \sum F_i * ln(\frac{y_i ^ {y_i}} {x_i^{x_i}}) = \sum F_i * W(x_i, y_i)$

где C - "скрытый код", F - веса ("фильтры"), x, y, - вероятности исходов, соответственно "до" и "после", W(x, y) - обозначение функции с логарифмом ("детали сюжетов").

"Скрытый код" (ранее, здесь и далее) - объективно не термин, а обозначение концепта. Вероятность "после" стоит в числителе, так вычитается, уже имея минус перед суммой. Понятие веса введено искусственно, но в целом оно отражает что разные исходы могут иметь +/- разное значение.

Пример с нечестной монеткой

Мы кинули 100 раз нечестную монетку, и 20 раз она упала орлом, а 80 решкой. После чего мы приняли решение что-то с монеткой сделать, и она стала падать 50/50.

C = ln(0.5**0.5 / 0.2**0.2) + ln(0.5**0.5 / 0.8**0.8) ~ 0.024 + 0.168 = 0.192 > 0

Больше нуля, в рамках наших весов (1; 1) означает хорошо. Если бы веса стояли как (1; -1), то есть если бы мы хотели чтобы решка выпадала чаще - то мы бы своё положение ухудшили.

Если бы этот "скрытый код" как-нибудь прогнозировался, то его вычисление - есть его осуществление, так как в нём участвуют его финальные результаты. Прежде чем попробовать его спрогнозировать рекуррентной (а какой еще) нейросетью (что и было бы программой), неплохо посмотреть на функцию W(x, y) - одна её форма уже любопытна.

При прочих равных повезет в трети случаев

Нет, это не уточнение "правила Парето", или "принципа хрупкости хорошего" из математической теории катастроф.

Упомянутая W(x, y) имеет такие формы в 3D, и такие свойства, в зависимости от множителя F (который можно поставить перед ней):

Случай F = 1

Отношение площади > 0 ко всей площади поверхности: ~ 0.298.

Случай F = 1/3

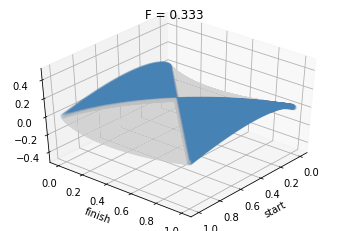
Отношение площади > 0 ко всей площади поверхности: ~ 0.328.

Случай F = 2

Отношение площади > 0 ко всей площади поверхности: ~ 0.282.

Ну и для интереса - симметричная ситуация F = -1

Хорошая ситуация достижима далеко не всегда, и даже не очень малые шевеления весов не слишком меняют ситуацию.

Экстраполяция и интерпретация

Можно брать амёбу конечно, как ей удается такими маленькими ~~ложно~~ножками... но нет, для примера я взял датасет YouTube Trending Videos. Сгруппировал по каналам и датам видео, взял сумму для одной даты, а далее:

Лайки, - ну с ними всё понятно,
Дизлайки, тоже ничего сверхъестественного,
Остальные - это все просмотры за минусом лайков и дизлайков.

Я почему-то подумал, что они в сумме образуют просмотры. Зарядил ту же сеточку, с весами (1; -1; 1) - хоть и наивно и грубовато, тем не менее жизнеспособно.

На входе сети 8 последних значений "скрытого кода", на выходе - следующий.

В целом, со схожими метриками прогнозируется как и для одного канала, так и для 10 и для 30 (и для RU, и для US отдельно). Ниже на картинках для топ-1 по количеству видео канала из русского сегмента, потом по топ-30 для русского и US соответственно (train/test 50/50).

А вот с интерпретацией всё не очень хорошо в том смысле, что

нейросети не интерпретируются. Пробовал конечно и линейки, и через jax подгонял свои функции - ну хуже, даже при использовании прошлых распределений,
справа внизу - это суммы кодов по убыванию в TOP по количеству видео. То есть частота попадания в трендовые не совсем несет светлое-доброе-вечное с точки зрения моих варварских весов. Но как известно, у YouTube там свой алгоритм, с учетом того, сколько поделились, и прочего. А у меня - свой :)

Но до некоторой степени "скрытый код" прогнозируется, тем более что я на бесплатном Google Colab особо никакие Optuna не запускал.

Это может и не доказательство жизнеспособности концепции, но некоторое свидетельство.

Смазанное заключение

В целом, задача бенчмарка с точки зрения "достигли ли желаемого" может быть оценена и в других (более привычных) попугаях - рублях, процентах конверсии и так далее. Но это что касается бизнеса. А если сравнивать в деньгах неизмеримое, но при этом действующее - может даже и способ. Веса только предмет извечной борьбы экспертов.

И есть подозрение, что если смотреть не сумму кодов для бенчмарка, а кумулятивную сумму - то она есть некоторый эквивалент жизненного цикла. Но проверку такой гипотезы надо катать не на отфильтрованном наборе данных (трендовых видео, как это было сделано), а на каком-то более сыром и менее дискретном.

Философские же замечания просьба не принимать близко к рассмотрению - я не философ, и даже не любитель. Но какая некоторая кривая меня к идее вывела - постарался изложить.

Тетрадку с кодом можно найти на gist.

Еще раз напомню, статья на популярное изложение особо не претендовала (я не копирайтер, и иногда даже жалею об этом), на научные открытия тоже. Долго искал подходящий хаб для публикации, и лучше этого одного больше ничего не нашел.

Тем не менее, надеюсь, кто-то нашел общие со мной мысли, или нашел мой численный эксперимент интересным. Спасибо за чтение.

P.S. КДПВ by Russian DALL-E по заголовку статьи.