Как правильно дифференцировать дискретные функции (Часть 1. Тестируем и улучшаем Numpy) / forpes.ru

Главная
Как правильно дифференцировать дискретные функции (Часть 1. Тестируем и улучшаем Numpy)

Как правильно дифференцировать дискретные функции (Часть 1. Тестируем и улучшаем Numpy) +6

09.08.2023 09:11

mikko_kukkanen 19 1000 Источник

После того как я реально «подсел» на чтение Хабра, захотелось «освежить» что‑то из своего богатого математического прошлого. Воскресить, так сказать, старые наработки, зайдя, естественно, через дверь с табличкой Python. Предлагаемая публикация посвящена простейшим методам численного дифференцирования. Как ни странно, тут возникают кое-какие вопросы и проблемы. Если тема будет для кого‑то интересной и полезной, в последующих публикациях будут рассмотрены более сложные вопросы и «продвинутые» расчетные алгоритмы. Поработаем с ОДУ (обыкновенными дифференциальными уравнениями, и, возможно, дойдем до ~~нашего Вильяма Шекспира~~ решения краевых задач УРЧП (уравнений в частных производных), в том числе нелинейных по краевым условиям и на адаптивных сетках.

Под термином "численное дифференцирование" часто понимают три разные вещи (цитата по numdifftools) - символьное (символическое) дифференцирование, вычисление производной от функции, заданной аналитически, и вычисление производной от функции, заданной набором данных. По первому и второму пунктам, вкратце

здесь

Для символьного (символического) дифференцирования функций в Python есть хорошо известная библиотека SymPy, по сути являющаяся большим структурированным справочником.

В SciPy существовал модуль scipy.misc, который теперь deprecated, и вместо него предложены два репозитория: https://github.com/maroba/findiff и уже упоминавшийся https://github.com/pbrod/numdifftools. Оба они, насколько мне удалось разобраться, относятся именно ко второму пункту, когда дифференцируемая функция задана аналитически, а производную нужно вычислить в конкретной точке, иногда с заданной точностью.

А мы займемся пунктом третьим - численным дифференцированием дискретных функций (они же решетчатые функции, они же табличные функции, они же функции, заданные набором данных и т.п.). Как оказалось, в библиотеках Python с этим не все так просто и безоблачно, как по идее должно бы быть. SciPy вообще про другое, а в NumPy "тема не раскрыта". На простейших примерах рассмотрим то, что предлагает NumPy, что там не так и как можно сделать лучше. .

Постановка задачи

Начнем с вычисления производной функции от одной переменной, заданной значениями $f_{i}$ в точках (узлах) $x_{i}$ с индексом на отрезке , разделенном на сегментов. Естественно, $x_{0} = a, \quad x_{n} = b$ . Для начала можно ограничиться равномерным шагом, при этом

$x_{i}=a+ i*h,\quad h=(b-a)/n$

Любому студенту-первокурснику известна формула

$f^{'}_{i+1/2} = (f_{i+1} - f_{i}) / h\quad\quad\quad(1)$

где символ слева - значение производной функции в точке, лежащей посередине между точками $x_{i}$ и $x_{i+1}$ Важный момент - в реальных численных расчетах, особенно для краевых задач, в том числе для УРЧП, вычисление производных в "промежуточных" точках очень неудобно, часто бывает необходимо хочется знать их в узлах отрезка $x_{i}$ или узлах сетки $(x_{i}, y_{j})$ для 2-мерных или $(x_{i}, y_{j}, z_{k})$ для 3-мерных задач. Естественно, это можно сделать большим количеством способов, самый простой из них это так называемая 3-точечная схема, которая в случае равномерной сетки превращается в 2-точечную:

$f^{'}_{i} = (f_{i+1} - f_{i-1}) / 2h\quad\quad\quad(2)$

Также существует 5-точечная схема, и так можно продолжать до бесконечности. Проблема у этих схем возникает в концах отрезка $x_{0}$ и $x_{n}$ поскольку у узла $x_{0}$ отсутствует соседний узел слева, а у $x_{n}$ - справа. В 5-точечной схеме ситуация еще хуже, поскольку для расчета нужно уже по 2 дополнительных узла слева и справа за границами исследуемого отрезка . С этим что-то надо делать. Далее мы посмотрим, что есть на эту тему в Numpy, потестируем на примере простейших функций типа экспоненты, и посмотрим что можно улучшить.

Экспонента удобна в качестве исследуемого объекта, потому что сразу понятно что должно получиться в результате - что-то вроде самой исходной функции. Все численные ошибки будут сразу видны.

Итак, возьмем функцию $f(x)=e^{x}$ на отрезке . Разобьем этот отрезок на частей с шагом и посчитаем значения функции в узлах $f_{i}=f(x_{i})$ , где $x_{i}=i*h$ . В качестве исследуемого объекта получается дискретная функция, заданная массивом значений из 11 элементов:

$[1.000,1.105,1.221,1.350,1.492,1.649,1.822,2.014,2.226,2.460,2.718]\quad\quad(3)$

Соответственно, в качестве результата операции численного дифференцирования мы должны получить его же, или что-то близкое к нему. Не очень наглядно смотреть на результаты в численном виде, но без этого трудно будет обойтись. Функция достаточно гладкая, как не посчитай, все получается похоже, и на графиках разница в третьем знаке после запятой не будет очень заметна. Но без графиков тоже никуда не деться.

Что предлагает NumPy

В Numpy удалось найти всего две функции на эту тему - diff и gradient. Чтобы на "рябило в глазах" от обилия цифр, сразу приведем график численных решений с помощью этих функций в сравнении с ожидаемым "точным" решением test (3):

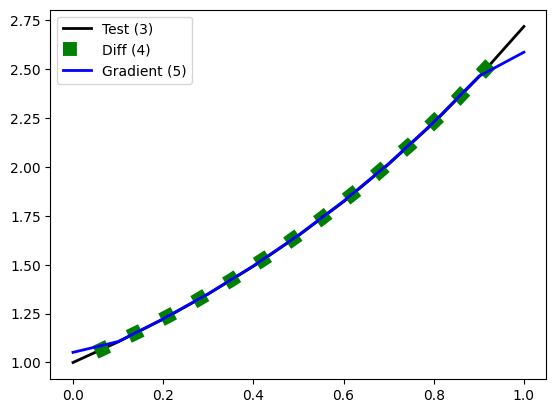
Видно, что в средней части отрезка графики трудно различимы, проблемы возникают вблизи концов отрезка, поэтому дальше будем подробно рассматривать ситуацию именно в окрестности этих "проблемных" точек.

Итак, подробнее. Применяя к исходному массиву (3) функцию diff, получим следующий массив значений производной:

$[1.052 ,1.162, 1.285, 1.420, 1.569, 1.734, 1.916, 2.118, 2.341, 2.587]\quad\quad(4)$

Легко проверить, что, результат посчитан по 2-точечной схеме (1), при этом точки хорошо ложатся на точное решение, однако размерность массива уменьшилась на единицу. Конечно, процедура имеет право на существование, но как уже было отмечено, это не подходит для многих практических случаев. С функцией gradient результат вычисления производной выглядит по-другому:

$[1.052, 1.107, 1.223, 1.352, 1.494, 1.651, 1.825, 2.017, 2.229, 2.464, 2.587]\quad\quad(5)$

Тут уже сохранена размерность исходного массива, можно сравнить его элементы с значениями исходной функции (3), и заметить, что ошибка возникает только в третьем знаке после запятой везде, кроме конечных точек, в которых получается ну очень непохоже на правду. Легко проверяется, что “внутренние” значения массива посчитаны по 3-точечной схеме (2). Вместе с тем, значения в конечных точках совпадают с конечными значениями в “2-точечном” решении (4), т.е граничные значения в функции gradient взяты из решения diff (посчитаны по 2-точечной схеме (1)). Так себе “гибрид” получается, но, как говорится, “не стреляйте в пианиста, он играет как может”.

А что, так можно было?

Как можно “улучшить” решение (5) в граничных точках? Все на самом деле проще некуда. Вспомним разложение функции в ряд Тейлора в окрестности левой граничной точки отрезка $x_{0}$ и применим его для приближенного вычисления значений функции в точках $x_{1}$ и $x_{2}$ отстоящих от граничной точки на h и 2h, соответственно:

$f(x_{1}) = f(x_{0}) + h*f^{'}(x_{0})+ h^{2}/2*f^{''}(x_{0})$ $f(x_{2}) = f(x_{0}) + 2*h*f^{'}(x_{0})+ (2*h)^{2}/2*f^{''}(x_{0})$

Исключая из этой системы уравнений значение второй производной $f^{''}(x_{0})$ , которое нас пока не интересует, легко получить выражение для вычисления искомого значения производной $f^{'}$ в точке $x_{0}$ :

$f^{'}(x_{0}) = (-3*f(x_{0}) + 4*f(x_{1})- f(x_{2}))/2h\quad\quad(6.1)$

Аналогичным образом выводится формула для вычисления значения производной $f^{'}$ в точке $x_{n}$ :

$f^{'}(x_{n}) = (3*f(x_{n}) - 4*f(x_{n-1})+ f(x_{n-2}))/2h\quad\quad(6.2)$

“Скорректировав” функцию gradient в граничных точках (если интересно, код на Python в 2-х версиях можно посмотреть

здесь

def gradient_improved_1(f, h):
  n = len(f) - 1
  y1 = np.append(y[1:], 3 * y[n] + y[n-2])
  y1[0] *= 4
  y2 = np.insert(y[:-1], 0, 3 * y[0] + y[2])
  y2[n] *= 4
  return (y1-y2)/2/h


def gradient_improved_2(f, h):
  n = len(f) - 1
  y1 = np.append(np.insert(y[2:], 0, 4*y[1]), 3 * y[n] + y[n-2])
  y2 = np.append(np.insert(y[:-2], 0, 3 * y[0] + y[2]), 4*y[n-1])
  return (y1-y2)/2/h

В результате получим следующий массив значений:

$[0.996, 1.107, 1.223, 1.352, 1.494, 1.651, 1.825, 2.017, 2.229, 2.464, 2.710]\quad\quad(7)$

Результат выглядит уже достаточно красиво. Сравнить результаты diff (4), gradient (5) и improved (7) с точным решением (совпадающим со значениями исходной функции) test (3) можно также на графике вблизи левой границы отрезка :

Аналогична ситуация вблизи правой границы отрезка:

"Улучшенная" функция показывает прекрасные результаты. Более наглядную картину, возможно, можно было бы получить, “накопив ошибки” при повторении процедуры дифференцирования несколько раз. Точное решение при этом, естественно, не меняется, но подсчеты по стандартным функциям NumPy “разъезжаются” настолько сильно, что лучше не портить себе настроение. С другой стороны, преимущества “улучшенной” процедуры уже очевидны, график почти "ложится" на точное решение.

Что дальше?

Если разбираться до конца, то, конечно, надо проверить предложенную процедуру на других функциях, например, полиномиальных или тригонометрических. Возьмем в качестве следующего примера на том же отрезке функцию $f(x) = x^{3}$ , шаг сетки оставим тот же, результат вычисления производной будем сравнивать с точным решением $f^{'}(x)=3*x^{2}$ . Сначала о хорошем - ситуация вблизи правого конца отрезка:

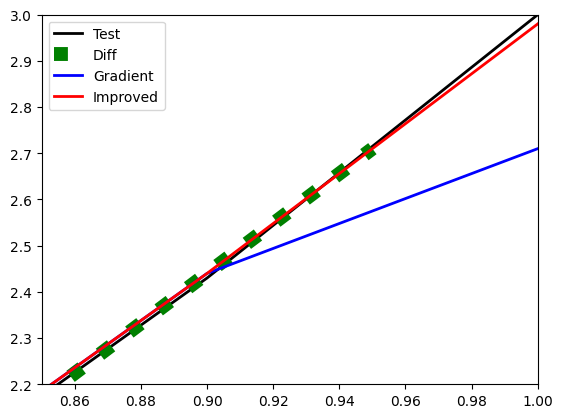
Все похоже на ситуацию с экспонентой: diff “не доходит до конца”, gradient дает большую ошибку в крайней точке, “улучшенный” gradient выглядит очень хорошо, практически совпадая с точным решением.

Ситуация вблизи левого конца отрезка, мягко говоря, уже не совсем однозначна:

Наш улучшенный алгоритм improved в окресности точки 0 уступает “оригинальному” алгоритму gradient, и при этом они оба достаточно далеки от “идеала” - точного решения test. Достаточно легко понять, что такая ситуация возникает, если первая производная дифференцируемой функции в этой точке близка к нулю.

Возникает закономерный вопрос - а можно ли придумать алгоритм, не требующий увеличения вычислительных затрат ( а в нашем случае, это О(n)), но дающий лучшие результаты на всем отрезке, включая его концы? Конечно, можно, это и будет темой следующей статьи. Спасибо за внимание. Буду благодарен за комментарии.

Комментарии (19)

lazy_val
09.08.2023 10:23
#25840628
+1
jax.grad с allow_int = True не пробовали?
1. mikko_kukkanen Автор
  09.08.2023 10:23
  #25841246
  +1
  Спасибо за комментарий. Обязательно попробую. Я, собственно, собирался про МКЭ сразу писать с переходом на 2- и 3-мерные задачи. Там с визуализации и градиентные методы и т.д. Только неожиданно застрял в Numpy. Оказывается, к opensource радо аккуратно относиться. Причем всегда :))
  1. mikko_kukkanen Автор
    09.08.2023 10:23
    #25842798
    Попробовал. Если задать функцию аналитически, выдает производную в точке или на массиве точек. Это не то, что нужно. Как ни пытался "запихнуть" массив значений в аргументы jax.grad ( в том числе как return функции целочисленного аргумента), не получилось. Возможно, не догоняю.

adeshere
09.08.2023 10:23
#25841078
+2
Мы решали похожую задачу методом экстраполяции тренда. На границах ряда это позволяет избежать укорочения сигнала, а внутри сигнала - единообразно с границами обрабатывать перерывы и пропуски. Пример того, как это работает для одного частного случая, можно найти вот

в этой статье
Ссылка на статью, а ее текст можно взять вот здесь или вот здесь.
Но, это все сделано не на питоне, а в собственном

пакете для анализа временных рядов

Описание и программы можно скачать вот отсюда, а исходные тексты лежат вот здесь. Но у нас достаточно

специфические данные и задачи
ряды только эквидистантные, но с кучей пропущенных наблюдений, а обработка в скользящем окне обычно включает несколько итераций разными методами. Поэтому длина сигнала при использовании алгоритмов скользящего окна не должна уменьшаться
и пакет заточен строго под их решение, поэтому его сложно назвать универсальным.

К тому же это все написано

на кондовом фортране

с кучей зависимостей между разными функциями, так что вытащить из него какие-то отдельные процедуры проблематично. А пытаться прицепить весь пакет -

безнадежно
как сказал один наш коллега, заглянув внутрь - "у них там свой Excell"
.

Да и идеология у нас немного другая: наш пакет - это фактически не готовые решения, а скорее конструктор, из которого надо самому собирать алгоритм, подходящий к той или иной ситуации.

только вот

сборка этого алгоритма происходит не методом написания кода, а путем выполнения нужных процедур

в интерфейсе
по принципу "график" - "вычисления" - "график"
в результате чего получается не программа, а в лучшем случае макрокоманда на очень примитивном собственном языке. Сейчас мы бы уже сделали по-другому, но ноги всей этой системы растут из 1980-х годов, когда даже такая архитектура была откровением. Так с тех пор и прикручиваем к старому ядру всякие финифлюшки по принципу "работает-не трогай!"

В общем, конкретные функции оттуда вытащить сложно, а вот идеи - пожалуйста.
1. mikko_kukkanen Автор
  09.08.2023 10:23
  #25841222
  Спасибо за комментарий. Обязательно посмотрю. Если занимались временными рядами, слышали про теорему Такенса? Все про нее говорят, но конкретики я нигде не нашел.

aamonster
09.08.2023 10:23
#25841328
+1
А почему у вас на последнем графике линия Test с изломом?

ЗЫ: и чтоб два раза не бегать – s/окресности/окрестности/
1. mikko_kukkanen Автор
  09.08.2023 10:23
  #25841542
  Как только из аналитической функции получен массив значений, о ней (этой функции) забываем. Работаем только с дискретными значениями. В последнем графике помещаются только три узла, поэтому виден излом. Вообще-то, лучше точки поставить, но тогда не очень красиво будет. Интерполяции между точками пока не касаемся. Без пропавшей согласной писал интуитивно. Наверное, когда в школе учился, можно было и так и так. А сейчас, наверное, лучше попрапавить. Спасибо.
  1. aamonster
    09.08.2023 10:23
    #25841598
    +1
    Не надо забывать о функции: через те же точки проходит бесконечное множество кривых, с производными по вкусу (см. интерполяционные полиномы – правда, я не помню, в какой их разновидности можно производные задавать, но она есть... Ну или обычный b-сплайн).
    
    Т.е. для вашего набора точек любое из решений может оказаться верным, поэтому есть резон указать ограничения на функцию (для стандартных методов – обычно это ограничение на модуль второй производной)
    
    Ну и задача с шумом, которую тут упомянули, ещё интереснее.
    
    mikko_kukkanen Автор
    09.08.2023 10:23
    #25841992
    Согласен. Верных решений много, выбор зависит от разных факторов, например от вычислительных затрат, или от степени гладкости и т.д. В следующей публикации напишу еще об одной интересной задаче, недавно опубликованной на Хабре (если я ее, конечно, правильно понял). На самом деле каждая конкретная задача требует своего подхода. Может быть неправильным ограничивать модуль второй производной.
    
    aamonster
    09.08.2023 10:23
    #25842112
    С модулем второй производной – просто очень легко доказывается, что погрешность вычисления производной будет не больше максимума этого самого модуля на "рабочем отрезке", умноженного на длину того самого отрезка и какую-то константу. Вот этим и пользуются. Это по трём точкам. По пяти – вылезает, соответственно, четвёртая производная (так что считай вы по пяти точкам – последний график бы чётко лёг на эталон) и куб длины отрезка.
    
    Но при наличии шума всё опять хуже, интерполяция высоких порядков начинает проигрывать. Вроде тут в идеале нужен плюс-минус тот же подход,что в фильтре Калмана, когда изначально у нас сигнал и шум, шум оцениваем и аппроксимируем с его учётом... Ну а по-простому – интерполяция низких порядков, да производные по отрезку подлиннее, или заранее сгладить исходные данные. Интересно, что у вас в статье будет.
    
    mikko_kukkanen Автор
    09.08.2023 10:23
    #25842140
    Наилучшая аппроксимация в окрестности точки (тут, конечно, по пяти точкам точнее будет) - не всегда основное требование. В методе конечных элементов, о котором напишу в продолжении этой публикации, основная идея - наилучшая аппроксимация "в среднем" по всему отрезку. Кроме этого будет рассмотрена одна случайно образовавшаяся задача, где как раз надо принимать решение - какое ограничение накладывать на вторую производную по всему отрезку. Надеюсь, Вас также заинтересует.
    
    Конкретно в этой публикации можно было сразу начать с 5-точечной схемы, также придумав какой-нибудь костыль по краям, там уже по 2 точки "отвалятся". Но это все-таки именно костыли, что неправильно идеологически.
    
    aamonster
    09.08.2023 10:23
    #25842266
    О, метод конечных элементов – прям как маслом по сердцу, студенческие годы вспомнил (кафедра гидрогазодинамики, там числяка много было).
    
    Надеюсь, вы его в приложении к условно-реальным задачам опишете – когда на элемент сразу накладываются законы сохранения.
    
    mikko_kukkanen Автор
    09.08.2023 10:23
    #25842594
    Понимаете, какая штука. Дифференцирование функции одной производной хоть МКР хоть МКЭ - не слишком увлекательное занятие. Я решил на эту тему написать публикацию только потому, что обнаружил, что в библиотеках Python нет соответствующей адекватной процедуры. Почти то же самое с ОДУ. По задаче Коши много чего, а по краевым задачам немного и невнятно. Но основной интерес, конечно в 2- и 3-мерных задачах. Я в свое время много чего "в стол" написал, кстати в МДТТ. Вот тут самое интересеное должно быть.
    
    aamonster
    09.08.2023 10:23
    #25842130
    А, и ещё: будет не лень – проверяйте методы на функции exp(-1/x²). Очень интересная функция, непрерывная, гладкая, но не раскладывается в ряд Фурье (точнее, Мак-Лорана – в окрестности нуля).
    
    mikko_kukkanen Автор
    09.08.2023 10:23
    #25842150
    Конечно, попробую код погонять.Только я в конце концов в диффуры хочу уйти, в том числе, в частных производных. По дифференцированию максимум еще одна публикация планируется. Хотя кто знает ...

adeshere
09.08.2023 10:23
#25841410
+2
слышали про теорему Такенса

Нет, на практике я с такими задачами не встречался. Как я понимаю, идея там простая и сводится к анализу траекторий в фазовом пространстве с учетом их возможного искажения шумом. Но на практике это будет работать только для стационарных сигналов. А почти все без исключения экспериментальные временные ряды - нестационарны. Начиная от геофизики и кончая макроэкономикой и социологией. Если об этой нестационарности "подзабыть", можно сделать массу интересных открытий ;-) И это относится не только к корреляциям, но и к любым другим методам.

Да, мы всегда пытаемся повысить отношение сигнал/шум, накапливая данные (и неявно при этом предполагая, что полезный сигнал повторяется, а шумы случайны). Но делать это бессмысленно, если измеряемый сигнал каждый раз относится к разным явлениям, а не к одному и тому же. Никто ведь не будет сегодня измерять суточный ход температуры у гриппозного больного, завтра у обезьянки, послезавтра у крокодила, потом в комнате, а потом это все осреднять. Все понимают, что эти явления разные. Однако почему-то считается совершенно нормальным измерять один и тот же показатель на протяжении многих лет, и без каких-либо проверок постулировать априори, что раз мы ежедневно измеряли одно и то же, то значит вправе наши измерения осреднять, вычислять дисперсии-корреляции и т.д. Хотя любая нестационарность изучаемого процесса совершенно четко и однозначно указывает:

нет, это не одно и то же!

На самом деле при повторяющихся измерениях очень важно учитывать: изменилось ли то окружение, в котором протекают наши процессы. Если оно стало другим - то мы измеряем уже какую-то иную величину, хотя и датчики, и вольтметры по-прежнему стоят под той же самой горой. То есть, имеем дело со случайным процессом, а значит, уже не вправе применять для анализа этих рядов аппарат, разработанный для случайных величин.

На первый взгляд, это может показаться буквоедством и формалистикой, но вы удивитесь, к каким катастрофическим последствиям может приводить игнорирование этого факта. За примерами снова отсылаю вот к этой статье.

Но если у нас не случайная величина, а что-то другое, то вопрос по возможности применения большинства типовых методов статистического анализа для таких данных требует особого изучения. Так как говоря строго, условия их применимости уже однозначно нарушены. И пока мы не выясним, какие последствия из этого могут быть, любые попытки содержательного анализа результатов такой обработки фактически беспредметны.

P.S. Точнее, в лаборатории стационарные временные ряды, наверно, бывают. Но вот у нас в геофизике я с ними за много лет еще ни разу не сталкивался.
1. mikko_kukkanen Автор
  09.08.2023 10:23
  #25842014
  +1
  В лабораторной физике хотя бы формально можно много раз повторить один и тот же эксперимент. Однако даже в прогнозирования финансовых рядов часто предполагают "стационарность". Хотя тут даже терминологией теории вероятностей пользоваться некорректно.

nUser123
09.08.2023 10:23
#25841418
+4
На практике приходится работать с зашумленными данными. Подсчет производной вышеприведенными способами приводит к усилению шума, причем довольно существенно. Я использую следующий способ - считаю линию в окрестности текущего значения по методу наименьших квадратов и в качестве производной беру тангенс угла наклона этой линии (k из уравнения y=kx+b). Окрестность подбирается под наибольшую частоту спектра исходной функции без учета шумов.
1. mikko_kukkanen Автор
  09.08.2023 10:23
  #25841968
  Спасибо за важный комментарий. Обработка зашумленных данных - отдельная важная задача. Часто бывает не до производных, а просто надо "сгладить" экспериментальные данные. Я бы к этому вопросу подходил системно: определил базис функций, на котором будет проводиться аппроксимация, определил меру (например, $L_{2}$ ), а после этого Вы автоматически попадете в сопряженные аппроксимации, как наилучшие. Тут есть опасность "переборщить" со сглаживанием и потерять физику процесса. Я скоро выпущу часть вторую, коснусь темы МКЭ. Возможно, пройдусь по теории. Метод наименьших квадратов, конечно, имеет право на существование, но есть много альтернатив.

Как правильно дифференцировать дискретные функции (Часть 1. Тестируем и улучшаем Numpy) +6

Постановка задачи

Что предлагает NumPy

А что, так можно было?

Что дальше?

Комментарии (19)

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор