Как правильно дифференцировать дискретные функции (Часть 2. Все-таки, МКЭ?) / forpes.ru

Главная
Как правильно дифференцировать дискретные функции (Часть 2. Все-таки, МКЭ?)

Как правильно дифференцировать дискретные функции (Часть 2. Все-таки, МКЭ?) +15

24.08.2023 16:30

mikko_kukkanen 39 2800 Источник

В части первой обсуждались алгоритмы вычисления первой производной дискретной функции (функции, заданной массивом {аргумент: значение}, или массивом значений в узлах на равномерной сетке). Были протестированы функции Python numpy.diff и numpy.gradient (других в Python так и не нашлось), и был предложен алгоритм improved, который, как выяснилось, работает хорошо, но не всегда. При этом проблемы возникают на концах отрезка, на котором определена дифференцируемая функция. Во второй части поработаем с методом конечных элементов (МКЭ, Finite Elements Method), и попробуем построить алгоритм вычисления первой производной, наилучший по точности, и, по возможности, без “слабых мест”.

Во избежание разногласий (а они были в комментариях к части первой) еще разок об объекте исследования. В части первой было сделано одно не совсем корректное допущение. Все исследуемые массивы "визуально" были представлены с точностью до 3-х знаков после запятой. Однако в расчетах использовались точные значения, сгенерированные функциями numpy.exp(x) или x**3. Точность, естественно, была ограничена ошибками машинного округления. Поскольку в этой части повествования мы действуем более аккуратно, то рассматриваться будут дискретные функции, заданные именно массивами с точностью до 4-го знака после запятой. Например, таким:

$[1.0000, 1.1052, 1.2214, 1.3499, 1.4918, …, 2.7183]\quad\quad(1)$

У этой дискретной функции есть прекрасное свойство - ее первая производная очень похожа на ее саму. Это свойство будет использовано для иллюстрации точности решений разными способами. А о том, что массив сгенерирован экспонентой, забываем и запрещаем в коде использовать функцию numpy.exp(x).

Кроме массива (1) будут исследованы еще несколько других массивов. На них можно посмотреть здесь:

Массивы (дискретные функции) для исследования

Сгенерировано кубической параболой на отрезке :

Первая производная для оценки точности результатов:

Сгенерировано функцией на отрезке $[0, \pi/2]$ :

Первая производная для оценки точности результатов:

Про дискретную функцию (1) мы также знаем, что эта функция задана на отрезке , разделенном на части с равномерным шагом h=0.1. Алгоритм numpy.diff мы из рассмотрения исключим, как “наихудший” из-за несохранения размерности массива данных, и соревнование будет проводиться между остальными двумя ( numpy.gradient и improved), а также новыми алгоритмами, построенными на МКЭ.

Немного теории. Нудновато, но полезно

Я поначалу хотел убрать теоретическую часть в скрытый текст, но в результате получилось совсем немного математики, и, скорее, определение используемых терминов, к которым далее по тексту приходится часто возвращаться.

В рассматриваемом случае МКЭ фактически означает аппроксимацию искомой функции (а также ее первой и даже второй (!!!) производных) кусочно-линейными функциями с последующим решением системы линейных уравнений относительно параметров аппроксимации. Поэтому, если теория, коротко изложенная в этом разделе, покажется не очень простой для восприятия, этот раздел можно пропустить. Общая логика изложения должна быть понятна.

В описании МКЭ присутствует своего рода дуализм. Часто встречающаяся формулировка начинается с разбиения исследуемой области на мелкие части - собственно конечные элементы. В одномерном случае это отрезки, в двумерном - треугольники или 4-угольники, в трехмерном - тетраэдры и т.д. “Внутри” каждого элемента функция представляется достаточно простой, например, линейной. И далее строится система линейных уравнений для вычисления значений функций в узлах, минимизирующих некоторый функционал типа потенциальной энергии или функции ошибок. Мы пойдем другим, более формализованным путем, который (для начала, в одномерном случае) выглядит следующим образом:

Пусть на отрезке задано множество функций $\{f(x)\}$ , достаточно "хороших" для наших задач - не обязательно непрерывных, но хотя бы квадратично интегрируемых. Для всех таких функций определяется скалярное произведение, например:

$<f, g> = [\int_{a}^{b} f(x)g(x) \,dx]\quad\quad(2)$

, которое определяет меру (модуль функции) :

$\parallel f \parallel^2 \quad = \quad<f, f> \quad= \int_{a}^{b} f(x)^2 \,dx$

Кроме этого, на этом же отрезке задается конечный (что, вообще говоря, не обязательно) набор базисных функций (базис):

$e_i(x), \quad i=0,\quad … , \quad n$

Изначальная задача - найти набор констант

$a_i, \quad i=0,\quad … , \quad n$

таких, что линейная комбинация базисных функций с коэффициентами “наилучшим образом” аппроксимирует исследуемую функцию , т.е. обеспечивается минимум модуля их разности ( он же - функция ошибки, если придерживаться терминологии ML):

$\{a_i\} => min \quad \delta \quad = \quad min \int_{a}^{b} [f(x)- \sum \limits_{i=0}^n a_i*e_i]^2 \,dx$

Для этого необходимо равенство нулю всех частных производных

$\frac{\partial \delta}{\partial a_i}, \quad i=0,\quad... ,\quad n \quad\quad (3)$

Это и есть система n+1 линейных уравнений для нахождения n+1 неизвестных величин . В простейшей версии МКЭ для одномерного случая в качестве базисного набора функций выбираются “функции-крышки” - кусочно-линейные функции , такие, что

$e_i(x)=1 \quad при \quad x=x_i\quad и \quad e_i(x)=0 \quadпри\quad x\neq x_i$

В этом случае коэффициенты суть не что иное как приближенные значения функции в узлах сетки , что можно обозначить как $f(x_i) \quad \approx \quad a_i$ , а функция аппроксимируется конечно-линейной функцией - линейной комбинацией базисных функций:

$f(x) \quad \approx \quad\sum \limits_{i=0}^n a_i*e_i$

Важное замечание, в том числе, по терминологии

В дальнейшем изложении кусочно-линейная функция иногда будет называться вектором $\overline{a}$ . Этот вектор состоит из коэффициентов разложения функции по базису $\{e_i\}$ .

В общем случае, коэффициенты разложения , вообще говоря, не совпадают со значениями функции в узлах . Они близки к значениям функции в узлах только потому, что функции базиса выбраны специальным образом - "функций-крышек". Однако, если функция - кусочно-линейная и является линейной комбинацией "функций-крышек", то такое совпадение, очевидно, имеет место, и в этом случае функция сама является своей же точной аппроксимацией, и представима в виде вектора своих узловых значений, что и имеется в виду.

Опуская выкладки, итоговую систему линейных уравнений (3) можно представить в следующем виде:

$G * \overline{a} = \overline{<e, f>}\quad\quad (4)$

где G - квадратная матрица с компонентами $g_{ij}$ :

$g_{ij} = <e_i, e_j>$

где i, j = 0, …, n, вектор $\overline{a}$ - есть вектор-столбец из неизвестных величин , а вектор $\overline{<e, f>}$ -есть вектор-столбец из значений , где i = 0, …, n.

Матрица G как 2-мерный массив скалярных произведений базисных функций часто встречается в различных разделах математики типа дифференциальной геометрии или МДТТ, и имеет много красивых названий - фундаментальный тензор, метрический тензор, матрица жесткости и т.п. Соответственно, решение системы (4) можно представить в виде:

$\overline{a} = \overline{<e^*, f>}$

, где $\overline{<e^*, f>}$ - вектор-столбец из значений , и вектор $\overline{e^*}$ (эквивалентный набору векторов $\{e^*_i\}$ ) называется “сопряженным базисом” и находится по формуле:

$\overline{e^*} = G^{-1} * \overline{e}$

Рассмотренный выше метод аппроксимации функции называется, соответственно, методом сопряженных аппроксимаций или методом наилучших аппроксимаций. “Наилучшесть” понимается, естественно, в терминах меры или другой меры, выбранной для задания скалярного произведения функций.

На практике матрицу G обычно явно не обращают, поскольку это очень затратная операция. Полезное свойство матрицы G в нашем (одномерном) случае - трехдиагональность, т.е. все ее ненулевые элементы расположены на главной диагонали (i = j) и на двух соседних диагоналях (| i - j | = 1). При этом система уравнений (4) решается прогонкой, с количеством операций O(n).

Функции-компоненты сопряженного базиса также обычно не вычисляют, однако ниже мы впрямую встретимся с ними, что лично мне кажется достаточно эстетичным.

МКЭ способ 1 ("лобовой")

Итак, начинаем применять теорию на практике. В прошлом дискретная, а теперь кусочно-линейная функция задана массивом значений (1) на отрезке с шагом h = 0.1, т.е. набором значений . При этом:

$f(x)= \sum \limits_{i=0}^n f_i*e_i \quad\quad(5)$

где - элементы массива (1), а - "функции-крышки". Необходимо найти ее первую производную, или, если точнее, наилучшую аппроксимацию первой производной, “натянутую” на базис $\{e_i\}$ .

Важный комментарий для понимания алгоритма

Производная кусочно-линейной функции, если ее считать как обычно, будет кусочно–постоянной и не непрерывной функцией с "разрывами" в узлах , в которых производная не определена. В МКЭ мы ищем ее наилучшую (в смысле меры ) кусочно-линейную аппроксимацию, что можем сделать, вообще говоря, для функции любого вида.

Обозначим первую производную функции как $f^{'}$ , и будем искать ее аппроксимацию на множестве линейных комбинаций функций-крышек, т е. в виде

$f^{'}(x) \quad \approx \quad\sum \limits_{i=0}^n a_i*e_i$

, где значения сразу дадут нам искомые значение производной в узлах. Функция ошибки принимает вид:

$\delta \quad = \quad \int_{a}^{b} [f^{'}(x)- \sum \limits_{i=0}^n a_i*e_i]^2 \,dx \quad\quad (6)$

Раскрываем квадратные скобки под интегралом, “выкидываем” первое слагаемое, поскольку оно не зависит от , и при дифференцировании все равно пропадет, затем ко второму слагаемому применяем интегрирование по частям, после этого система уравнений (3) (про равенство нулю всех частных производных $\delta$ по принимает вид:

$G * \overline{a} = f_n- f_0 -\overline{<{e^{'}}, f>} \quad\quad(7)$

где и - суть первый и последний элементы массива (1), соответственно, а $\overline {<e^{'}, f>}$ - вектор из скалярных произведений первых производных базисных функций $e^{'}_i = (e_i)^{'}$ и исходной функции . Поскольку базисные функции кусочно линейны, их производные $e^{'}_i$ будут кусочно-постоянны, и легко интегрируются.

Конкретный вид матрицы жесткости G и правой части уравнения (7) здесь:

$G = \begin{vmatrix} h/3 & h/6&0&... & 0& 0 & 0\\ h/6 & h/3 & h/6 &0&...& 0 & 0\\0 &h/6&h/3&h/6&0&...&0\\...&...&...&...&...&...&...\\...&...&0&h/6&h/3&h/6&0\\...&...&...&0&h/6&h/3&h/6\\...&...&...&0&0&h/6&h/3\end{vmatrix}$

Вектор-столбец в правой части уравнения (7):

$\begin{vmatrix} (f_1-f_0)/2\\ (f_2-f_0)/2\\...\\(f_{k+1}-f_{k-1})/2\\...\\(f_n-f_{n-2})/2\\(f_n-f_{n-1})/2\end{vmatrix}$

Как уже говорилось выше, решаем систему прогонкой, поскольку матрица жесткости - трехдиагональная. Результаты расчета по новому алгоритму FEM представлены на рисунках.

Рис.2. Сравнение алгоритмов на левом конце отрезка

Рис.3. Сравнение алгоритмов на правом конце отрезка

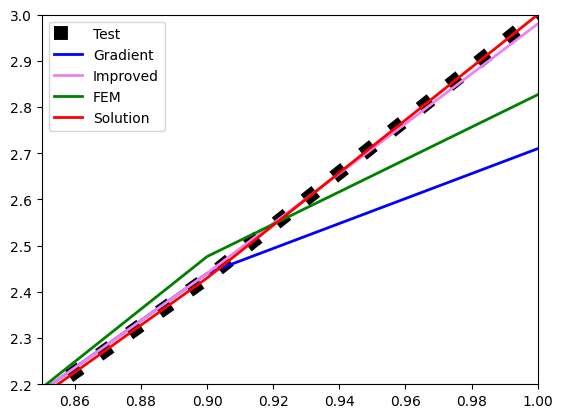
В середине отрезка у всех 3-х алгоритмов точность примерно одинакова, а проблемы, как обычно, на концах. При этом FEM устойчиво показывает результаты лучше, чем numpy.gradient, но хуже, чем improved.

Алгоритм FEM был также протестирован на дискретном аналоге кубической параболы . Вблизи нуля ситуация поменялась в лучшую для FEM сторону:

Рис.4 Кубическая парабола на левом конце отрезка

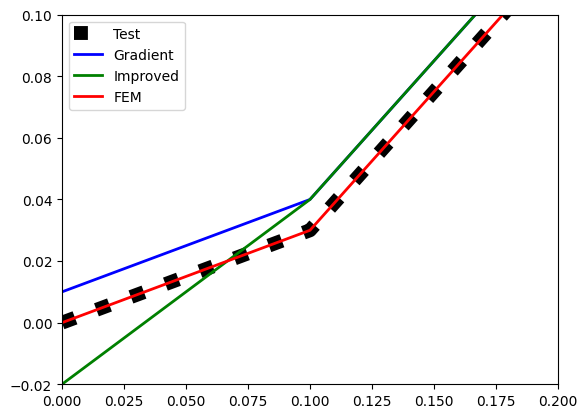
На левом конце отрезка FEM практически точно ложится на тестовое решение. Вблизи правого конца отрезка "расклад сил" похож на Рис.3.

Подводя итог этого раздела, можно заключить, что "лобовой" метод расчета первой производной с использованием МКЭ ( в его простейшей версии, с "функциями-крышками") устойчиво лучше, чем метод numpy.gradient, но не дает существенного преимущества по сравнению с алгоритмом improved. Возможно ли все-таки на основе МКЭ построить что-то получше? Оказывается, да.

МКЭ способ 2 ("продвинутый")

В основе этого алгоритма лежит, на первый взгляд, парадоксальная идея - чтобы точнее посчитать первую производную функции, надо сразу считать вторую производную. Аналогично выражению (6) представим функцию ошибки для второй производной функции в виде:

$\delta \quad = \quad \int_{a}^{b} [f^{''}(x)- \sum \limits_{i=0}^n a_i*e_i]^2 \,dx \quad\quad (8)$

где $f^{''}(x)$ - вторая производная функции , которая, в свою очередь, представлена выражением (5). Казалось бы, вторая производная кусочно-линейной функции - тождественный (кроме точек разрыва) ноль. Ан нет, все не так просто. Повторяем процедуру так же, как в прошлом разделе. Раскрываем квадратные скобки под интегралом, “выкидываем” первое слагаемое, поскольку оно не зависит от , и при дифференцировании все равно пропадет, ко второму слагаемому применяем интегрирование по частям, после этого система уравнений (3) (про равенство нулю всех частных производных функции ошибки $\delta$ по переменным принимает вид (аналогично уравнению (7)):

$G * \overline{a} =f^{'}_n - f^{'}_0 - \overline{<e^{'}, f^{'}>} \quad\quad(9)$

где $f^{'}$ - первая производная функции , т.е. кусочно-постоянная функция, которая легко интегрируется в произведении с производными базисных функций $e^{'}_i$ - тоже кусочно-постоянными функциями, а $f^{'}_0$ и $f^{'}_n$ - значения первой производной на левом и правом концах отрезка , соответственно. При всем этом -

значения $f^{'}_0$ и $f^{'}_n$ заранее неизвестны и пока непонятно, откуда их взять.

Какая при этом получается система линейных уравнений? Матрица жесткости G остается такой же, как в предыдущем разделе (см. спрятанный текст выше), а вектор в правой части уравнения (9) (обозначим его $\overline{b}$ ) заслуживает подробного рассмотрения. Его можно представить в виде трех слагаемых:

$\overline{b} = \overline{b_{base}} -f^{'}_0*\overline{b_0}+f^{'}_n*\overline{b_n}$

Подробный вид слагаемых-векторов можно посмотреть здесь:

$\overline{b}=\begin{vmatrix} (f_1-f_0)/h - f^{'}_0\\ (f_2-2*f_1+f_0)/h\\...\\(f_{k+1}-2*f_k + f_{k-1})/h\\...\\(f_n-2*f_{n-1}+f_{n-2})/h\\f^{'}_n - (f_n-f_{n-1})/h\end{vmatrix}$ $\overline{b_{base}} = \begin{vmatrix} (f_1-f_0)/h \\(f_2-2*f_1+f_0)/h\\...\\(f_{k+1}-2*f_k + f_{k-1})/h\\...\\(f_n-2*f_{n-1}+f_{n-2})/h\\ - (f_n-f_{n-1})/h\end{vmatrix}$ $\overline{b_0} = \begin{vmatrix} 1\\0\\...\\0\\...\\0\\0\end{vmatrix} \quad\quad \overline{b_n}=\begin{vmatrix} 0\\0\\...\\0\\...\\0\\1\end{vmatrix}$

А значит, решение системы системы уравнений (9), представленной в виде:

$G*\overline{a} = \overline{b} \quad\quad(9.1)$

в свою очередь, представимо в виде:

$\overline{a} = \overline{a_{base}} -f^{'}_0*\overline{a_0}+f^{'}_n*\overline{a_n} \quad\quad(10)$

где $\overline{a_{base}}, \quad\overline{a_0}, \quad\overline{a_n}$ - решения 3-х систем линейных уравнений с одной и той же матрицей жесткости G и векторами в правой части $\overline{b_{base}}, \quad\overline{b_0}, \quad\overline{b_n}$ , соответственно. Эти три вектора-решения являются представлениями кусочно-линейных функций, “разложенных” по базису $\{e_i\}$ , причем компоненты каждого вектора являются коэффициентами при базисных "функциях-крышках" в этом разложении. Вектора ( т.е. функции) $\overline{a_{base}}, \quad\overline{a_0}, \quad\overline{a_n}$ для нашего исследуемого массива (1) представлены на рис.5.

Рис.5. Решение "base" и две функции из сопряженного базиса

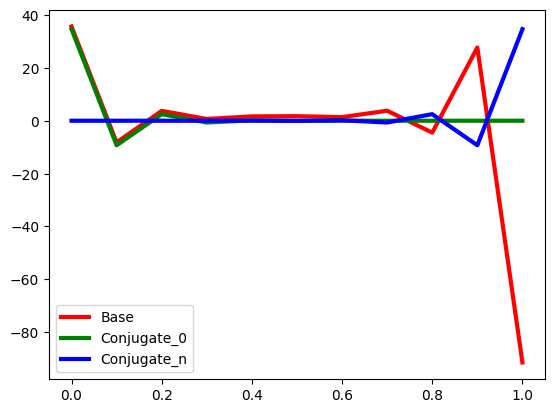
Зеленый и красный графики почти сливаются на левом конце отрезка, поскольку разница между ними порядка 1, а масштаб рисунка по вертикали значительно больше (значение в нуле порядка 40). Заметим, что вектора $\overline{a_0}$ и $\overline{a_n}$ - не что иное как представление двух функций из сопряженного к $\{e_i\}$ базиса, а именно, функций и . Вот мы и встретились с сопряженным базисом, как было обещано в начале публикации.

Задача нахождения вектора $\overline{a}$ из выражения (10) поначалу выглядит достаточно сложной. Необходимо провести оптимизацию по двум параметрам $f^{'}_0$ и $f^{'}_n$ , причем цель оптимизации (типа минимизации какой-то новой функции ошибки) пока даже не сформулирована. Но если внимательно посмотреть на Рис.5, то можно заметить, что все три вектора из (10) имеют ярко выраженной "пилообразный" характер. Поэтому сформулируем:

Цель оптимизации - вычисление вектора $\overline{a}$ , соответствующего "наименее пилообразной" функции, т.е. наиболее гладкой аппроксимации $f^{''}$

На рис.5 хорошо видно, что для обоих участвующих в процессе сопряженных вектора $\overline{a_0}$ и $\overline{a_n}$ вся их пилообразность “сосредоточена” вблизи концов отрезка - вблизи левого конца отрезка для вектора (функции) с номером 0 (зеленый цвет) и вблизи правого конца отрезка для вектора (функции) с номером n (синий цвет). Сформулируем две гипотезы:

Гипотеза 1. Оптимизацию выражения (10) по двум параметрам $f^{'}_0$ и $f^{'}_n$ можно проводить независимо по каждому параметру отдельно. Первый будет отвечать за “гладкость” искомого вектора $\overline{a}$ ( т.е. функции $f^{''}$ ) слева, а второй - справа.

Гипотеза 2. В качестве “меры пилообразности” можно взять угол между первым и вторым звеньями ломаной $\overline{a}$ для нахождения оптимального значение параметра $f^{'}_0$ и угол между последним и предпоследним звеньями ломаной $\overline{a}$ для нахождения оптимального значения параметра $f^{'}_n$ . Вычислять будем косинус угла между звеньями, который, естественно, должен быть максимален в обоих случаях. Оптимизацию (поиск максимума косинуса) можно проводить разными хорошо известными методами, мы на этом останавливаться не будем.

Для оконгчательного решения поставленной задачи осталось по узловым значениям второй производной ( а это - вектор, он же набор узловых значений $\overline{a}$ ) восстановить набор узловых значений первой производной, например, так:

$f^{'}_{i+1} = f^{'}_i+h*(a_{i+1}+a_i)/2,$

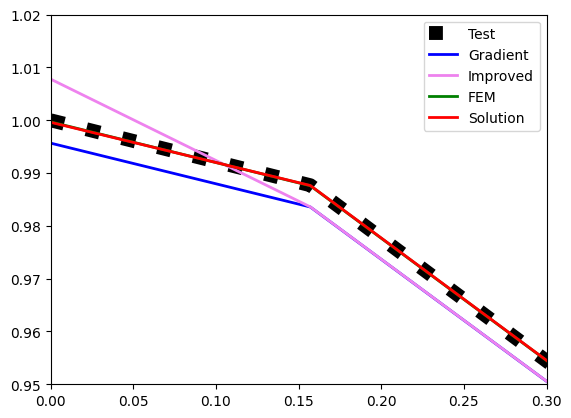
где $f^{'}_0$ определено как значение первого параметра оптимизации. Оказалось, что эти две гипотезы прекрасно работают. Посмотрим на результат (solution) и сравним его с альтернативами. Сначала для экспоненты (ой, обещал забыть название функции):

Рис.6. Решение Solution соревнуется только с Improved и побеждает

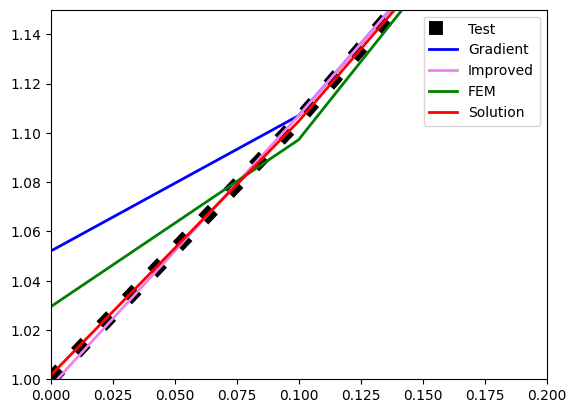
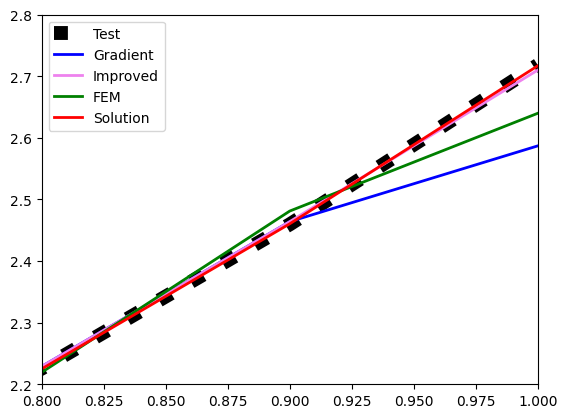
Теперь для кубической параболы (ой, опять вспомнил название):

Рис.8. На левом крае Solution практически совпадает с FEM, оба побеждают

Похоже, solution по точности превосходит остальные алгоритмы. Причем, как также выяснилось, не только на концах отрезка. Во внутренних точках его точность также выше.

По секрету сообщаю, что сравнил результаты для функции $f=sin(x), \quad x\in[0,\pi/2]$ .

Результат здесь:

Слева: Solution опять соревнуется только с FEM

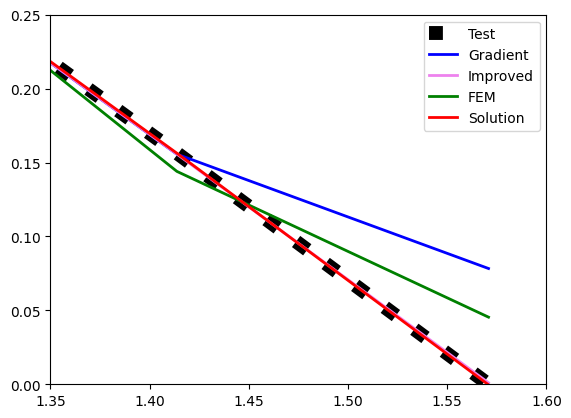
Пожалуй, на этом пора заканчивать вторую часть изложения, и так довольно объемно получилось. Похоже, вызревает третья часть. Я все-таки не выполнил обещанное коллеге по результатам обсуждения публикации. Держу в запасе еще один алгоритм нахождения первой производной, который движется ближе к интерполяции. Собственно, из него и возникла идея нахождения второй производной как непрерывной кусочно-линейной функции. Но, как часто бывает, тема сама собой увела в сторону модификации на основе МКЭ.

Наверное, в третью часть также добавлю Python-листинг. Пока код существует в Jupiter Notebook и требует доведения до презентабельного вида. Ну и кое-какие мелочи еще требуется доработать.

Спасибо за внимание. Буду благодарен за комменты и отзывы.

Комментарии (39)

lazy_val
24.08.2023 19:16
#25895308
+3
Добрые люди советуют апроксимировать дискретную функцию сплайнами, и дальше аналитически считать первую (вторую, ...) производную.

Другие добрые люди аж целую книжку на эту тему запилили. Ну или вот.

Понятно что кубическим сплайнами дальше третьей производной мы не продвинемся, но нам по условиям задачи вроде только первая нужна.
1. mikko_kukkanen Автор
  24.08.2023 19:16
  #25895422
  +2
  Большое спасибо за интерес к теме и за ссылки. Здесь, например, приведена формула "односторонней производной" (one-side difference), которую я и предложил в части первой для "улучшения" функции numpy.gradient на границах отрезка. Только не пойму, почему разработчики библиотек python этого не знают, или не хотят знать. А кто-то ведь им доверяет и пользуется тем, что есть.
  
  Касательно сплайнов - при всем уважении к этому методу, требование аппроксимации функции точно проходить через узловые значения функции осложняет алгоритм. И скорее всего (я не проверял), не дает наилучшую аппроксимацию по мере . По другой мере, пожалуйста, только это уже другой метод. А какой лучше - попробуй определи. Скорее всего, зависит от практической задачи. В части третьей дам алгоритм ближе к практической постановке, и там реально получается кубическая интерполяция.
  
  На прошлой неделе беседовал со своим большим другом, который лет 20 назад занимался расчетом форм для отливок из пластмассы и штампов для корпусных деталей к автомобилям. Оказывается, там нужна неперывная третья производная. Иначе отражение на поверхности автомобиля будет некрасивым.
  
  А книжка, на которую Вы также дали ссылку, сотку баксов стоит. При всей моей любви к науке, именно на это потратить не готов. У меня, все-таки другие научные интересы.
  1. lazy_val
    24.08.2023 19:16
    #25895492
    ...книжка ... сотку баксов стоит
    
    Google Books предлагают в свободном доступе пусть и немного "усеченную", но вполне рабочую версию.
    
    Насчет "наилучшей апроксимации" согласен, все зависит от задачи.
    
    Спасибо огромное за продолжение, жду с нетерпением (правда :) ) третьей части.
    
    mikko_kukkanen Автор
    24.08.2023 19:16
    #25895506
    +1
    Третья часть, наверное, будет примерно через месяц. Есть еще два-три "горячих" пирожка на другие темы. Хочу сначала их опубликовать.
    
    lazy_val
    24.08.2023 19:16
    #25895510
    Вот кстати ребята запилили некий МКЭ с участием (в том числе) B-сплайнов. Базируясь, насколько я смог понять, на разработках Micula & Micula
    
    mikko_kukkanen Автор
    24.08.2023 19:16
    #25895562
    Понимаете, какая штука. В классическом понимании МКЭ подразумевает разделение области на небольшие части (КЭ), аппроксимацию искомой функции на каждом из этих КЭ чем-нибудь простым - линейной (простейший случай), или полиномиальной или даже тригонометрической функцией с последующей "склейкой" решений на границе соседних элементов. Если эти функции "сосредоточены" внутри одного КЭ и его соседей, то матрица СЛУ будет иметь околодиагональный вид, и СЛУ можно легко решать. Для сплайнов, помоему, получается 5 диагоналей, что уже сложнее, чем 3, но тоже терпимо. Можно развиваться в сторону усложнения этих функций. Это - один путь.
    
    С другой стороны, если подходить к МКЭ как методу наилучших (сопряженных) аппроксимаций, то функции базиса могут быть ненулевыми хоть на всем отрезке или области. Пример. Аппроксимируем функцию на множестве полиномов. Если в качестве меры выбрать метод минимальных квадратов (а почему нет?), то Вы получите полином Лагранжа, т.е бяку. Если вы выберите , то аппроксимация будет вполне себе гладкой. Только матрица СЛУ получается "заполненной". Можно двигаться в этом направлении.
    
    Можно комбинировать эти подходы и получать новые методы. Важно оченивать точность и вычислительные затраты.
    
    На самом деле, МКЭ в одномерном случае - это из пушки по воробьям. Основное преимущество МКЭ - возможность решать 2- и 3-мерные задачи в УрЧП, причем в областях с криволинейной границей. Этим, я собственно, когда-то занимался, и сейчас постепенно вспоминаю. А вот на сплайны в 2- и 3- мерных случаях интересно было бы увидеть. Возможно, последняя ссылка об этом, там точно двумерные сетки. Посмотрю.
    
    Tiriet
    24.08.2023 19:16
    #25895800
    Был такой метод Ритца- где идея была такая- вот есть решение, давайте возьмем какой-нибудь базис функций на всей области решения, и найдем наилучшую аппроксимацию наших уравнений этим базисом. А дальше все Ваши рассуждения про L2-норму, свертки функций и минимизацию отклонений- и получалась большая плотная матрица. А потом базис из функций, заданных на всей области решения заменили на базис из финитных функций (имеющих ограниченную область поддержки, то есть, ненулевых только в каком-то небольшом объеме)- и получился МКЭ. Причем, МКЭ на симплексных сетках (одномерный МКЭ, двумерный на треугольных сетках, трехмерный на тетраэдрах) строго совпадает с конечными разностями на этих же сетках, потому что и в МКЭ и в конечных разностях базисная функция- линейная, а раз базисы одинаковые- то и аппроксимация одна и та же, хотя формулы и выглядят по разному. Но у МКЭ получилось гораздо лучше разнести операции- построение сетки- это одно, построение базиса на этой сетке- это другое, построение СЛАУ на этом базисе под эту задачу- это третье, решение СЛАУ- это четвертое. И эти операции друг с другом вообще никак не связаны, а это сильно упрощает разработку софта, реализующего вычислительную мат-физику. Выбор типа элемента никак не затрагивает построение сетки, и никак не влияет на решение СЛАУ. Физическая задача ничего не знает об элементах, она только задает функцию, которую надо минимизировать. Основное преимущество- это не возможность решать задачи в 3D- основное преимущество- это очень хорошая структурированность подхода и минимальное количество связей между отдельными операциями. и хорошо обусловленная матрица, так как элементы- конечные и матрица всегда будет разреженная. Правда, для таких матриц есть и недостатки- итерационные решения для них медленно сходятся.
    
    mikko_kukkanen Автор
    24.08.2023 19:16
    #25897522
    С основной идеей Вашего комментария абсолютно согласен. Только МКР и МКЭ близки только в одномерном случае. МКР в 2-мерном случае можно, конечно, построить на прямоугольниках. А как на треулольниках - не очень понятно.
    
    Кроме всего прочего, МКЭ прекрасно решает задачи в вариационной постановке, а для некоторых задач это очень полезно.
    
    Касательно итерационных методов для 2-D и 3-D задач. Метод сопряженных градиентов дает точное (!!!) решение за N итераций, где N - число неизвестных. Я как раз в него погружаюсь :))
    
    Tiriet
    24.08.2023 19:16
    #25897912
    +1
    на треугольнике строится точно такая же разностная аппроксимация первого порядка точности- в точности как и конечноэлементная: представьте, что в одномерном случае конечная разность, деленая на шаг по координате- это на самом деле интеграл по поверхности, деленый на стягиваемый этой поверхностью объем, просто объем одномерный, а поверхность- две нульмерные стороны. это позволяет обобщить конечные разности на любое число измерений :-).
    
    вариационность постановки задачи не связана с элементами :-). вариационные задачи сами по себе лучше решаются, чем другие постановки, потому что и требования по гладкости у них ниже, и законы сохранения в них выполняются по построению, а это для численных схем вкусный бонус. если у Вас в физической задаче энергия и импульс сохраняются- то Ваши результаты будут всегда правдоподобными. могут быть полной туфтой, но при этом все равно будут выглядеть правдоподобно, и будет сложно понять, что они тутфта :-).
    
    про сопряженные градиенты- ну да, дает. если у Вас вычисления всегда идут с абсолютной точностью. А так-то он он не очень устойчив. я не знаю, что там у Вас за задача, но для МДТТ, гидродинамики и электродинамики от CG, BCG и их вариаций народ массово уходит на всякие CORS, TFQMR, TFQMORS и другие методы на подпространствах Крылова- у них сходимость сильно лучше, чем у CG/BCG. при такой же доказательности сходимости к точному решению. И они не требуют самосопряженности разностных операторов, что иногда (почти всегда) весьма желательно и очень ускоряет расчет. И если я правильно помню, эта сходимость строгая, если вы храните все промежуточные решения, а у Вас памяти столько нет и не будет, чтоб на хорошей сетке хранить все промежуточные решения. А без них- только медленное сползание куда-то в район решения, но без гарантий его достижения. И есть еще ряд результатов, которые намекают на то, что наилучшая сходимость среди всех итерационных методов достигается на multigrid-методах, чисто теоретически- потому что обычные итерационные завязаны на норму невязки, а невязка низкочастотных мод решения всегда очень и очень маленькая, и низкочастотные моды любыми методами ловятся крайне плохо, а мультигриды эффективно повышают частоту этой невязки на грубых сетках и ускоряют сходимость прямо феноменально. но там оператор загрубления построить не так-то вдруг, хотя есть подход algebraic multigrid, который вроде как строит наилучший оператор загрубления для любой разреженной матрицы (безотносительно сеток и вообще ее природы), но это неточно, проверять надо.
    
    mikko_kukkanen Автор
    24.08.2023 19:16
    #25898004
    Я как раз приверженец вариационных постановок. А за подробный комментарий по-поводу итерационных методов спасибо. Буду иметь в виду.
    
    Я когда-то давно считал 2-D задачи МДТТ (не бог весть какое достижение, естественно). Упор был на нелинейность по граничным условиям (типа "отлипания" границы от опоры), там была "фишка". Сейчас хочу воскресить наработанное для 3-D. Только вот "застрял" на обычном дифференцированиии.
  1. Tiriet
    24.08.2023 19:16
    #25898022
    Только не пойму, почему разработчики библиотек python этого не знают, или не хотят знать.
    
    все они прекрасно знают и понимают.
    
    The gradient is computed using second order accurate central differences in the interior points and either first or second order accurate one-sides (forward or backwards) differences at the boundaries. The returned gradient hence has the same shape as the input array.
    
    потому что они выбрали самый быстрый и самый простой расчет градиента. и совершенно правильно сделали- для 99% задач этого хватает с головой. А кому не хватает- у тех своя голова, и они должны выбрать под свою однозначно специфическую задачу свой подходящий метод, которых миллионы, и всем не угодишь.
    
    mikko_kukkanen Автор
    24.08.2023 19:16
    #25898134
    Я не пойму, почему они пишут про "second order accurate one-sides (forward or backwards) differences at the boundaries "? У них же по факту не так. Точность второго порядка получается именно на one-side difference.
1. belch84
  24.08.2023 19:16
  #25896098
  Когда-то проэкспериментировал с различными методами численного дифференцирования при решении задачи реконструкции динамической системы по временнОму ряду. Способ со сплайнами был одним из тех, которые я пробовал. Он работал, но хуже, чем методы дифферецирования высших порядков, при которых производня вычисляется как конечная разность с определенными коэффициентами по некотрому (нечетному) количеству соседних точек (причем для практических целей удобно было устанавливать это кол-во различным для конкретых временнЫх рядов). Зато способ со сплайнами прекрасно работал при построении трубки для кривой, заданной набором точек в пространстве (там нужно при помощи численного дифференцирования вычислять нормали и бинормали)
  1. mikko_kukkanen Автор
    24.08.2023 19:16
    #25897830
    Сплайны - один из способов сглаживания, но далеко не единственный. МКЭ с "функциями-крышками" никакого сглаживания не даст, от кусочно-линейной функции никуда не денешься. Можно "расширить" базисные функции на на несколько соседних точек, и при кусочно-линейных базисных функциях, скорее всего, получится аналог 5-, 7- и так далее точечных схем МКР, о чем Вы также пишете. Но можно "расширенные" базисные функции сделать с непрерывными производными высших порядков, и тогда сглаживание будет так или иначе реализовано. В общем-то, сплайны вписываются в эту идеологию.
    
    Tiriet
    24.08.2023 19:16
    #25897950
    +1
    потому что совершенно разные задачи. Сплайн нужны там, где надо красиво сгладить какой-то набор данных и потом по этому сглаживанию красиво что-то изобразить. А МКЭ в силу его неявной но всегда используемой вариационной природы, обеспечивает отличное сохранение главных физических инвариантов- энергии там, массы, импульса, момента импульса и других физических инвариантов- эти инварианты гарантировано сохраняются в вариационной постановке задачи, и после дискретизации этой вариационной постановки конечными элементами тоже продолжают сохраняться. А для физики это сохранение энергии сто очков форы дает любой гладкости или красивости решений и все равно обыгрывает.
    
    mikko_kukkanen Автор
    24.08.2023 19:16
    #25898586
    Сплайны, как и вообще-то почти любые функции, можно использовать в качестве базисных для построения МКЭ. Коллега выше дал ссылку: Вот
    
    Tiriet
    24.08.2023 19:16
    #25899268
    Можно. Но для них сложно показывать порядок аппроксимации. А так да- SPH в слабой вариационной постановке- это, внезапно, МКЭ с одноузловым элементом и сплайном второго порядка для функции формы.

Refridgerator
24.08.2023 19:16
#25895812
+1
Если кому интересно, в ЦОС дискретные функции описываются при помощи специальных функций — Дельта-Дирака, Гребёнки Дирака, Хэвисайд-Тэты, и дифференцируются самым обычным способом, без каких-либо ухищрений.
1. Vytian
  24.08.2023 19:16
  #25897484
  Да можно вообще, прости господи, ДПФ/ДВП использовать, скорость неимоверная, памяти мизер надо. Но надо данные смотреть
  1. mikko_kukkanen Автор
    24.08.2023 19:16
    #25897494
    Расшифруйте, пожалуйста, аббревиатуру.
    
    Vytian
    24.08.2023 19:16
    #25897884
    Быстрое дискретное преобразование Фурье /быстрое дискретное вейвлет-преобразование. Соответственно, для дифференцтрования требуется просто линейная ренормировка спектральных компонент, и обратное преобразование. Ну, для вэйвлетов чуть сложнее, но и вычислительно гибче
    
    mikko_kukkanen Автор
    24.08.2023 19:16
    #25897902
    +1
    Я в свое время копался в этих методах, но уже подзабыл. По-моему, то и другое сильно зависят от наличия гармоник в данных (в спектре). Если гармоник нет, будет проблема со сходимостью. При этом, как я уже писал в ответах на комментарии, в 1-D случае можно много всего напридумывать. А попробуйте решить хотя бы 2-D УрЧП в области с криволинейной границей. Я на Хабре задал этот вопрос спецу по БПФ, в ответ - молчание.
    
    Vytian
    24.08.2023 19:16
    #25898030
    Слава богу, преобразования Фурье линейны, так что сколько там измерений все равно, в том числе и в scipy.fft. структура данных неважна, но есть тонкости с фазой и нормировками.
    
    mikko_kukkanen Автор
    24.08.2023 19:16
    #25898052
    Очень часто проблема именно в тонкостях (дьявол всегда в деталях)
    
    Vytian
    24.08.2023 19:16
    #25898084
    Криволинейные границы я бы решал дополнением данных нулями и аподизацией на границах, ну если надо быстро.
    
    Или посмотрел, не лучше ли локально в полярные/сферические координаты перейти, и кусочно по каким нибудь полиномам Лежандра или что там.
    
    Но вообще надо для себя решить принципиальные вопросы: Вам вычислительно простой метод нужен, или есть какое-то априорное знание о характере данных, или предельно общий случай, или максимально масштабируемый, данные ограниченные или потоковые.... да много чего. У меня, разумеется, своий набор подходов, оптимальный для моих задач. В крайнем случае, надо литературу читать, наверняка Вашу узкую задачу кто-то уже пытался решить.
    
    mikko_kukkanen Автор
    24.08.2023 19:16
    #25898112
    +1
    У меня задача - "раскочегарить" собственный мозг. Это не шутка. Я математикой занимался больше 30 лет назад.
    
    Vytian
    24.08.2023 19:16
    #25898656
    +2
    Дело благородное. Я то числами не от хорошей жизни занимаюсь, но она , жизнь, то есть, заставляет: вот крайний раз Био-Савар в Вашем любимом МКЭ не сходился, так что дифференцировал векторные потенциалы в разрывных гранусловиях ... а казалось бы, тривиальная, школьная почти задача --всего-то посчитать магнитное поле прямоугольной катушки с током с точностью в 8 знаков.
    
    Tiriet
    24.08.2023 19:16
    #25899274
    Вейвлет хаара, обобщенный на треугольники- я делал. Если это ДВП применять на производную искомой функции, то получается, неожиданно, многосеточный метод с отличной сходимостью.
    
    mikko_kukkanen Автор
    24.08.2023 19:16
    #25899278
    Я, в общем-то, не собирался заниматься дифференцированием функций. Просто логически начал с простого (как казалось поначалу) и затянуло. У меня есть старые наработки в МДТТ, новые в ML, а пока разминаюсь.
    
    Tiriet
    24.08.2023 19:16
    #25897958
    +2
    дискретное Фурье и вейвлет преобразования, наверно. только какое отношение ДПФ имеет к конечным элементам? ДПФ рулит там, где мы ОДУ во времени решаем, а МКЭ- где мы ДУ ЧП (диф.ур. в частных производных) решаем. Фурье можно иногда заюзать для решения ДУ ЧП, но в специфических случаях. В обычных практических задачах, когда коэффициенты уравнений по пространству меняются- там Фурье не дает каких-то волшебных преимуществ. А вот вариационная постановка и выполнение законов сохранения- дают.
    
    Vytian
    24.08.2023 19:16
    #25898678
    Задача поставлена -- дифференцирование скалярного поля. ДУЧП -- это вопрос отдельный, несоразмерный поставленной задаче, и вообще бессмысленный в обобщённой формулировке. Ну, по крайней мере менее чем в 2х томах ;)
    
    Узкая, но частная задача, где нужно дифференцировать скалярные или векторные потенциалы, известные, например, из МКЭ -- описание нетривиальных магнитных систем, где иногда требуется высокая точность.
    
    mikko_kukkanen Автор
    24.08.2023 19:16
    #25898958
    Наверняка нужно придумывать что-то свое. Скорее всего мера не годится.
1. mikko_kukkanen Автор
  24.08.2023 19:16
  #25897490
  Не очень понятно, как "обычным" способом можно продифференцировать Дельта-функцию.
  1. Vytian
    24.08.2023 19:16
    #25897900
    Зачем "обычным", если производные известны аналитически и дискретизуются. Фокус смещён в разложение на компоненты с известными производными. Погуглите метод разложения на главные компоненты, он относительно лёгкий в вычислении, если памяти хватит, там куча частных упрощенных схем известно/можно наколхозить под задачу, типа какой-нибудь "гусеницы".
    
    А вообще Вы уверены, что книжка Калиткина по числам не даст вам ответов на все вопросы. Раньше в мизерных выч. мощностяхиобъёмах памяти всё грамотно делали.
    
    mikko_kukkanen Автор
    24.08.2023 19:16
    #25897926
    Если производные известны аналитически, это уже совсем другая задача, скорее к символьному дифференцированию. Но меня смущает существование (?) аналитической да еще и дискретизируемой производной Дельта-функции. Или одна обобщенная функция представляется через другие обобщенные функции? Возможно, Вы имеете в виду метод граничных элементов, когда общее решение представляется в виде комбинации фундаментальных.
    
    Vytian
    24.08.2023 19:16
    #25897994
    Я специально несколько раз упомянул слово "разложение": да, исходя из знания типичного характера данных зачастую оптимально раскладывать в функциональные ряды, если это вычислительно легко, а разложения ортогональны или приближенно ортогональны. А аналитическая функция или обобщённая, всё равно, главное табулировать осмысленно и аккуратно.
  1. Tiriet
    24.08.2023 19:16
    #25897966
    +2
    а никак. она только в обобщенных производных дифференцируется. но от обобщенных производных один шаг до вариационных постановок :-) а от них как в черную дыру засосет в МКЭ.
    
    mikko_kukkanen Автор
    24.08.2023 19:16
    #25898032
    Как веревочка ни вейся, ... доползешь до МКЭ
    
    Vytian
    24.08.2023 19:16
    #25898150
    Ну разумеется, если априорных данных нет. Но есть плохие данные с плохой сходимостью операций на них, типа фрактальных. И таких в жизни полно

Как правильно дифференцировать дискретные функции (Часть 2. Все-таки, МКЭ?) +15

Немного теории. Нудновато, но полезно

МКЭ способ 1 ("лобовой")

МКЭ способ 2 ("продвинутый")

Комментарии (39)

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор

mikko_kukkanen Автор