Опасность апофении в аналитике и способы ее предотвратить. Между ложью и историями, в которых фигурируют данные, очень тонкая грань.
Мозг человека обладает удивительной способностью во всем находить паттерны… но у этих паттернов обычно мало общего с реальностью. Мы можем увидеть образ кролика в облаке или лицо Элвиса в картофельных чипсах.

Видишь кролика и профиль Элвиса?
Подумайте о тесте Роршаха — людям показывают разные кляксы и спрашивают, что они видят. Вы не поверите насколько охотно наш разум находит ложные интерпретации случайных наборов данных.
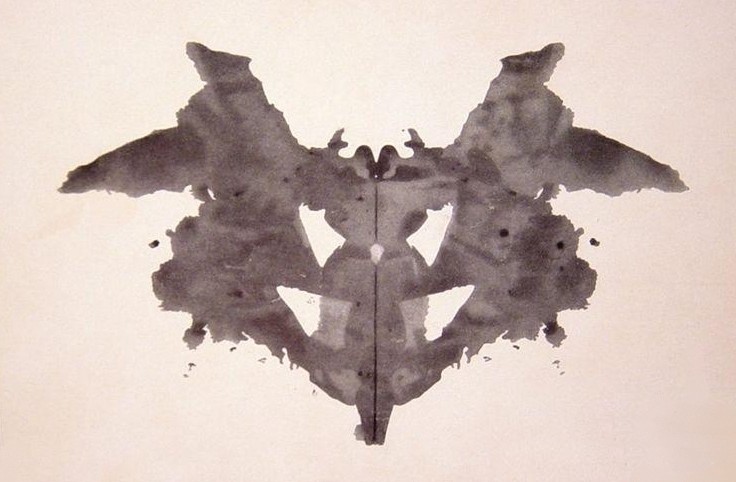
Летучая мышь? Бабочка? Обычная клякса? Это одна из 10 карт теста Роршаха, созданная в 1921 году.
У психологов есть красивое название этому явлению: апофения. Дайте людям хоть какой-то стимул и они найдут вам не только лица и бабочек, но и причину выделить бюджет на ваш любимый проект или запустить систему искусственного интеллекта.
В большинстве наборов данных много случайной информации. Какова вероятность, что ваша аналитика не подвержена апофении? Можно ли доверять своей интерпретации данных?
Чем больше способов фрагментации этих наборов данных и чем они сложнее, тем более расплывчатыми стимулами они являются. Они практически умоляют вас распознать в них ложные образы.
Вы уверены, что ваш последний набор данных не является скрытой апофенией?

Есть еще одно замечательное слово — парейдолия, своего рода это тоже апофения (находить знакомые вещи в расплывчатых сенсорных стимулах). В Японии есть даже музей камней, которые выглядят как лица. Мы живем в удивительное время.
Знаю, звучит мрачно, но я еще не закончила. Если вы проходите курсы по анализу данных, это может подлить масла в огонь. Студенты привыкли ожидать, что от каждого исследования данных нужно получить реальное значение. Каждое задание на поисковое исследование подразумевает скрытое сокровище. Только немногие профессоры решаются отправить вас в погоню за недостижимым (для вашего же блага!). Оценить задания без точного ответа сложнее, поэтому студенты обычно не особо обращают на них внимание.
Повествование данных это просто отход в сторону от вранья напрямую с использованием данных. Оставим в стороне вопрос о том реальны ли паттерны. Поговорим о множественных интерпретациях. Если вы видите в кляксе образ летучей мыши, это еще не значит, что там нет бабочки, костей таза или пары лис. Если бы я не упомянула лис, вы бы их увидели? Вероятно нет. Психологические механизмы, отвечающие за мотивацию и внимание, играют против вас. Чтобы перестать видеть летучую мышь и начать видеть лишь суперпозицию значений, требуется особый навык.
Проблема в том, что как только люди цепляются за свой любимый образ, им становится сложно развидеть его и увидеть другие образы. Люди склонны сильнее всего верить интерпретации, которая привлекла их внимание в первую очередь. Каждое новое найденное значение снижает мотивацию продолжать поиск. Жонглирование несколькими потенциальными историями без переоценки вашей любимой истории это большой, умственный труд. Увы, не каждый аналитик достаточно дисциплинирован для этого. На самом деле многие аналитики заинтересованы в том, чтобы «доказать» лишь одну сторону истории за счет исследования данных. Зачем развивать навыки, которые мешают вашему кошельку пополняться?
Есть несколько способ доказать историю, используя данные — честный и доскональный. Моя статья о фрагментации данных расскажет вам об этом больше. Исследовательский анализ данных не относится к этим способам. Исследования данных, в которых не подразумевается получение реального значения, напоминают ловлю рыбы. Цвет вашего светового меча зависит от используемой наживки.

Если вы примкнете к темной стороне, вы будете ловить на крючок доказательство, поддерживающее вашу теорию. Вы же уже и так «знаете», что она верная (поэтому можете продать ее какой-нибудь наивной жертве). Вы можете даже не осознавать, что ваш световой меч красного цвета, если вы искренне верите в объективность данных и свою непредвзятость.
Если у вас достаточно сложный (расплывчатый) набор данных вы найдете паттерн, который сможете подогнать под доказательство своей любимой истории. В этом вся прелесть теста Роршаха. К сожалению, с данными дело обстоит хуже, чем с кляксами. Чем более математический ваш метод, тем убедительней он звучит для тех, кто ничего в этом не смыслит.

Спутниковый снимок «лица на Марсе», которое многие люди воспринимают как доказательство существования пришельцев.
Те, кто отказывается принимать темную сторону, тоже рыбачат. Но они ловят нечто другое: вдохновение. Они ищут паттерны, которые могут быть интересными и убедительными, но не принимают их за доказательства, потому что умны. Вместо этого они занимаются непредвзятой аналитикой и стараются отметить у себя в голове как можно больше разных интерпретаций.
Для этого нужен зоркий глаз и скромный, непредвзятый разум. Хорошие аналитики не пытаюсь заставить заинтересованные лица увидеть только одну сторону истории. Вместо этого они мыслят творчески, чтобы превратить одни и те же данные в множество историй. Они представляют свои выводы так, чтобы вдохновить всех на последующие действия и при этом не вызвать у своего руководства желание свернуть горы из-за излишней самоуверенности.
Дисциплина, выработанная для поиска нескольких интерпретаций, является секретным оружием аналитика. Она позволяет держать в поле зрения настоящие сокровища, спрятанные в данных. Если вас отвлекает ложная информация, в которую вы верите из-за предвзятости, сложно обратить внимание на доказательства, указывающие в другом направлении. Зачем вообще что-то анализировать, если выводы заранее предопределены? Непредвзятость дает шанс сделать так, чтобы все старания были не зря.

Этот бутерброд с сыром на гриле был продан за 28 000$ на аукционе, потому что на нем изображена Дева Мария. А вы что здесь видите?
Черты, которые вы наверняка хотите ищите в хороших аналитиках:
Помимо всего перечисленного эта статья предлагает вам обратить внимание еще и на эти черты:
Наконец, если вы руководитель, убедитесь, что вы даете своим подчиненным правильные стимулы. Вы ищете аналитика данных или манипулятора данными? У них разное мышление и навыки. Выбирайте аналитика с умом и вознаграждайте за правильное поведение.

Забудьте про картофельные чипсы! Этот японский музей с камнями, напоминающими лица, превзошел всех.
Научная публикация: The Potato Chip Really Does Look Like Elvis! Neural Hallmarks of Conceptual Processing Associated with Finding Novel Shapes Subjectively Meaningful

Узнайте подробности, как получить востребованную профессию с нуля или Level Up по навыкам и зарплате, пройдя платные онлайн-курсы SkillFactory:
Психологическая ловушка в аналитике данных
Мозг человека обладает удивительной способностью во всем находить паттерны… но у этих паттернов обычно мало общего с реальностью. Мы можем увидеть образ кролика в облаке или лицо Элвиса в картофельных чипсах.

Видишь кролика и профиль Элвиса?
Подумайте о тесте Роршаха — людям показывают разные кляксы и спрашивают, что они видят. Вы не поверите насколько охотно наш разум находит ложные интерпретации случайных наборов данных.

Летучая мышь? Бабочка? Обычная клякса? Это одна из 10 карт теста Роршаха, созданная в 1921 году.
У психологов есть красивое название этому явлению: апофения. Дайте людям хоть какой-то стимул и они найдут вам не только лица и бабочек, но и причину выделить бюджет на ваш любимый проект или запустить систему искусственного интеллекта.
Об авторе: Кэсси Козырков — южноафриканский специалист по данным и статистике. Она основала подразделение Decision Intelligence в Google, где является главным научным сотрудником.
В большинстве наборов данных много случайной информации. Какова вероятность, что ваша аналитика не подвержена апофении? Можно ли доверять своей интерпретации данных?
Наш разум делает с данными то же самое, что и с кляксами
Чем больше способов фрагментации этих наборов данных и чем они сложнее, тем более расплывчатыми стимулами они являются. Они практически умоляют вас распознать в них ложные образы.
Сложные наборы данных практически умоляют увидеть в них то чего там на самом деле нет
Вы уверены, что ваш последний набор данных не является скрытой апофенией?

Есть еще одно замечательное слово — парейдолия, своего рода это тоже апофения (находить знакомые вещи в расплывчатых сенсорных стимулах). В Японии есть даже музей камней, которые выглядят как лица. Мы живем в удивительное время.
Ложь, наглая ложь и аналитика
Знаю, звучит мрачно, но я еще не закончила. Если вы проходите курсы по анализу данных, это может подлить масла в огонь. Студенты привыкли ожидать, что от каждого исследования данных нужно получить реальное значение. Каждое задание на поисковое исследование подразумевает скрытое сокровище. Только немногие профессоры решаются отправить вас в погоню за недостижимым (для вашего же блага!). Оценить задания без точного ответа сложнее, поэтому студенты обычно не особо обращают на них внимание.
Студенты привыкли, что за каждым набором данных скрывается правда.
Повествование данных это просто отход в сторону от вранья напрямую с использованием данных. Оставим в стороне вопрос о том реальны ли паттерны. Поговорим о множественных интерпретациях. Если вы видите в кляксе образ летучей мыши, это еще не значит, что там нет бабочки, костей таза или пары лис. Если бы я не упомянула лис, вы бы их увидели? Вероятно нет. Психологические механизмы, отвечающие за мотивацию и внимание, играют против вас. Чтобы перестать видеть летучую мышь и начать видеть лишь суперпозицию значений, требуется особый навык.
Как только люди цепляются за свой любимый образ, им становится сложно его развидеть
Проблема в том, что как только люди цепляются за свой любимый образ, им становится сложно развидеть его и увидеть другие образы. Люди склонны сильнее всего верить интерпретации, которая привлекла их внимание в первую очередь. Каждое новое найденное значение снижает мотивацию продолжать поиск. Жонглирование несколькими потенциальными историями без переоценки вашей любимой истории это большой, умственный труд. Увы, не каждый аналитик достаточно дисциплинирован для этого. На самом деле многие аналитики заинтересованы в том, чтобы «доказать» лишь одну сторону истории за счет исследования данных. Зачем развивать навыки, которые мешают вашему кошельку пополняться?
Какого цвета ваш световой меч?
Есть несколько способ доказать историю, используя данные — честный и доскональный. Моя статья о фрагментации данных расскажет вам об этом больше. Исследовательский анализ данных не относится к этим способам. Исследования данных, в которых не подразумевается получение реального значения, напоминают ловлю рыбы. Цвет вашего светового меча зависит от используемой наживки.

Если вы примкнете к темной стороне, вы будете ловить на крючок доказательство, поддерживающее вашу теорию. Вы же уже и так «знаете», что она верная (поэтому можете продать ее какой-нибудь наивной жертве). Вы можете даже не осознавать, что ваш световой меч красного цвета, если вы искренне верите в объективность данных и свою непредвзятость.
Исследования данных, в которых не подразумевается получение реального значения, напоминают ловлю рыбы.
Если у вас достаточно сложный (расплывчатый) набор данных вы найдете паттерн, который сможете подогнать под доказательство своей любимой истории. В этом вся прелесть теста Роршаха. К сожалению, с данными дело обстоит хуже, чем с кляксами. Чем более математический ваш метод, тем убедительней он звучит для тех, кто ничего в этом не смыслит.

Спутниковый снимок «лица на Марсе», которое многие люди воспринимают как доказательство существования пришельцев.
Те, кто отказывается принимать темную сторону, тоже рыбачат. Но они ловят нечто другое: вдохновение. Они ищут паттерны, которые могут быть интересными и убедительными, но не принимают их за доказательства, потому что умны. Вместо этого они занимаются непредвзятой аналитикой и стараются отметить у себя в голове как можно больше разных интерпретаций.
Лучшие аналитики пытаются найти как можно больше интерпретаций.
Для этого нужен зоркий глаз и скромный, непредвзятый разум. Хорошие аналитики не пытаюсь заставить заинтересованные лица увидеть только одну сторону истории. Вместо этого они мыслят творчески, чтобы превратить одни и те же данные в множество историй. Они представляют свои выводы так, чтобы вдохновить всех на последующие действия и при этом не вызвать у своего руководства желание свернуть горы из-за излишней самоуверенности.
Непредвзятость дает анализу данных шанс нести в себе какой-то смысл.
Дисциплина, выработанная для поиска нескольких интерпретаций, является секретным оружием аналитика. Она позволяет держать в поле зрения настоящие сокровища, спрятанные в данных. Если вас отвлекает ложная информация, в которую вы верите из-за предвзятости, сложно обратить внимание на доказательства, указывающие в другом направлении. Зачем вообще что-то анализировать, если выводы заранее предопределены? Непредвзятость дает шанс сделать так, чтобы все старания были не зря.

Этот бутерброд с сыром на гриле был продан за 28 000$ на аукционе, потому что на нем изображена Дева Мария. А вы что здесь видите?
Наймите отличного аналитика
Черты, которые вы наверняка хотите ищите в хороших аналитиках:
- Они не делают выводов, которые выходят за пределы данных, которые они исследуют.
- Они легко управляются с инструментами обработки данных и умеют быстро просматривать огромные массивы данных.
- У них есть необходимые знания предметной области, поэтому они реже тратят время заинтересованных сторон на мелочи.
- Они понимают, что их работа заключается в поиске вдохновения.
- Они визуализируют данные удобным и понятным для мозга способом, поэтому вдохновение приходит быстро.
- Они знают, что им нужно для тщательного отслеживания любой обнаруженной ими потенциальной информации (и к кому обращаться за помощью).
Помимо всего перечисленного эта статья предлагает вам обратить внимание еще и на эти черты:
- Они знают, что ум находит смысл там, где его нет, поэтому стараются не поддаваться ложным интерпретациям и не спешат с выводами.
- Они не пытаются продать вам историю с готовым решением, найденную за счет долгой возни с данными. Вместо этого они уклоняются от прямого ответа и смягчают факты, когда говорят о данных.
- Они достаточно дисциплинированы, чтобы придумать всему множество интерпретаций. Чем быстрее они могут предоставить множество объяснений и чем больше альтернатив они генерируют, тем круче они как аналитики. Попробуйте в следующий раз проверить этот навык на собеседовании, когда будете нанимать джедая-аналитика.
Наконец, если вы руководитель, убедитесь, что вы даете своим подчиненным правильные стимулы. Вы ищете аналитика данных или манипулятора данными? У них разное мышление и навыки. Выбирайте аналитика с умом и вознаграждайте за правильное поведение.

Забудьте про картофельные чипсы! Этот японский музей с камнями, напоминающими лица, превзошел всех.
Научная публикация: The Potato Chip Really Does Look Like Elvis! Neural Hallmarks of Conceptual Processing Associated with Finding Novel Shapes Subjectively Meaningful

Узнайте подробности, как получить востребованную профессию с нуля или Level Up по навыкам и зарплате, пройдя платные онлайн-курсы SkillFactory:
- Курс по Machine Learning (12 недель)
- Обучение профессии Data Science с нуля (12 месяцев)
- Профессия аналитика с любым стартовым уровнем (9 месяцев)
- Курс «Python для веб-разработки» (9 месяцев)
Читать еще
- Тренды в Data Scienсe 2020
- Data Science умерла. Да здравствует Business Science
- Крутые Data Scientist не тратят время на статистику
- Как стать Data Scientist без онлайн-курсов
- Шпаргалка по сортировке для Data Science
- Data Science для гуманитариев: что такое «data»
- Data Scienсe на стероидах: знакомство с Decision Intelligence


N-Cube
Вся статья набор манипуляций и откровенной лжи. Вот, фактически, основная картинка из статьи:

Подразумевается, что это — просто случайная клякса. Но это невозможно! Потому, что изображение симметрично относительно вертикальной оси (с очень небольшими искажениями для отвлечения внимания от этого факта). Разумеется, это не случайный объект, и мозг его интерпретирует соответственно. То, что эта ложь придумана давно, не дает автору статьи и перевода индульгенции на распространение этого дальше.
skillfactory_school Автор
Научная публикация: The Potato Chip Really Does Look Like Elvis! Neural Hallmarks of Conceptual Processing Associated with Finding Novel Shapes Subjectively Meaningful
N-Cube
Привести ссылку на научную работу, не имеющую отношения к теме разговора — явная манипуляция. Указанная вами публикация вовсе не о возможности существования симметричных случайных клякс.
Статья начинается, для отвлечения внимания, про образы в облаках и чипсах, потом приводится пример теста и заявляется, что в симметричной картинке люди лишь ошибочно не видят случайной кляксы (ложь), далее сообщается, что это известный эффект с красивым названием (для убедительности) и сразу же идет утверждение про бюджеты и системы искусственного интеллекта (вау). Потом приводится ссылка на «авторитет» и так далее, по накатанной у манипуляторов дорожке.
MagisterLudi
вы правы на 100%
DrPass
Вы слишком недооцениваете силу человеческой фантазии.
N-Cube
Причем тут фантазия? Случайная клякса не может быть (почти) идеально симметричной, это свойство биологических объектов. Посчитайте коэффициент симметрии картинки из статьи и сравните с коэффициентом симметрии бабочек. А теперь попробуйте найти случайную кляксу с таким же коэффициентом. Подсказка: это практически невозможно; модели клякс существуют и степень их возможной симметрии тоже изучена.
DrPass
Тогда и вам подсказка: от того, что случайную кляксу отразили по вертикальной оси, она перестаёт быть случайной кляксой?
MagisterLudi
Удельная энтропия снижается в 2 раза.
То есть отображенная клякса в 2 раза менее случайная, чем неотображенная.
N-Cube
Ошибаетесь — по определению случайной величины, все значения (пиксели картинки) случайны. При наличии симметрии это явно не так, то есть клякса плюс её симметричное отображение не является случайной, так как половина пикселов не случайны и предсказуемы. Другими словами, по половине кляксы можно предсказать вторую половину — значит, это не случайный объект.
N-Cube
Разумеется, перестает — поскольку случайным образом её получить невозможно. Случайная клякса это результат случайного процесса или процессов, и симметричной она быть не может. Могу уточнить, что такое «невозможно» — при возрастании количества пикселов в изображении такой кляксы вероятность ее случайного получения стремится к нулю.
DrPass
Вообще, не перестаёт. Если функция Random() возвращает вам случайное число, то её линейное преобразование (которым в том числе является вертикальное отражение) также будет возвращать случайное число.
Это если вам нужны аргументы. Ну а если по сути вопроса, поднятая вами тема вообще не стоит и выеденного яйца, от первого сообщения до последнего.
N-Cube
Ошибаетесь — линейное преобразование случайной величины есть случайная величина, но здесь речь про последовательность из исходной случайной величины и ее линейного преобразования. Вам поверить, так можно значение константы повторить сколько нужно раз (пусть даже с линейным преобразованием) и получить случайное распределение, что явно не так.
По сути вопроса — обсуждаемая статья одна из худших на хабре по передергиваю и манипулятивности. И они предлагают учить разработчиков? Вот ведь нашли где это "впаривать", простите...
DrPass
А почему не так? Энтропия, если она измерима, действительно уменьшится, но результирующее распределение также будет случайным.
N-Cube
Смотрите, зеркальное преобразование это линейное преобразование с коэффициентом k (то есть отражение по некоторой оси симметрии, для перпендикулярной к которой оси координат коэффициент будет -1). Берем начальное значение 1, его зеркальное преобразование равно k, исходное значение и его зеркальное преобразование составят последовательность 1,k. Случайная ли она? Нет, поскольку второй элемент полностью определен первым, а случайная последовательность по определению состоит только из случайных элементов.
DrPass
Мы говорили про случайное распределение, а не про случайную последовательность. Это разные вещи. И случайное распределение, в отличии от последовательностей, по своему определению отнюдь не требует, чтобы входящие в него случайные величины были независимыми. В данном случае мы просто получаем случайное распределение, в котором между парами случайных значений есть взаимная зависимость, только и всего.
MagisterLudi
Похоже, что человек на бытовом уровне разбирается что такое «случайное».
Есть энтропия по Шеннону.
У нас есть два набора данных: случайная клякса и та же клякса с зеркальным отображением.
Определим «случайность» кляксы как q, а «размер» как V. Тогда размер двойной зеркальной кляксы будет 2V, а степень «случайности» такая же — q.
Так как исходно изображение аналоговое — «акварель на бумаге», то q>?. Для генерации случайных чисел отлично подходит.
MagisterLudi
habr.com/ru/post/343014
www.random.org/analysis
N-Cube
Уже на личности переходите, кроме хамства, аргументов не осталось?
Вы пытаетесь сделать генератор случайных чисел из одного исходного значения. Берем одно случайное значение на плоскости и отражаем его, потом исходное и отраженное еще раз отражаем… и теперь вы утверждаете, что получили идеально случайное распределение (на плоскости). Очевидно, это не так. Это вы понимаете? Полученное изображение случайным не является, его структура полностью детерминирована использованным преобразованием(и). Человеческий мозг легко распознает такую симметрию и делает соответствующие выводы, совершенно другие, чем для исходной картинки (кляксы).
Получение случайной последовательности путем физических измерений давно используется, но если вы измеренные значения повторяете (пусть и преобразованными), такая последовательность становится не случайной.
N-Cube
Случайное распределение по определению это распределение случайной величины, где каждое последующее значение случайно и не зависит от предыдущих. Если мы на основании предыдущих значений (левая часть картинки) знаем распределение следующих (правая часть картинки), то это не случайное распределение по определению.
Вы пишите то о случайной величине, то о случайных величинах — это совсем не одно и то же. Понимаете, случайная величина это не одно значение, как вам кажется. Случайная величина Попросту говоря, это и некий метод (функция) получения последовательности случайных значений и сама эта последовательность.
DrPass
Да
Нет
Если бы второе было бы верным, не существовало бы целой прикладной математической отрасли, которая занимается выявлением корреляций разных факторов на основании их случайных распределений.
N-Cube
Определение случайной величины ясно говорит, что:
«Случайная величина (случайная переменная, случайное значение) — это математическое понятие, служащее для представления случайных явлений, когда для них может быть определена их вероятность, то есть мера возможности наступления.»
То есть нельзя определить следующее значение, может быть вычислена только вероятность получения некоторого значения.
Обратите внимание на разницу между известным законом распределения (определяет вероятность значений) и известными значениями. И корреляция работает именно с законами распределения:
«Корреля?ция (от лат. correlatio «соотношение, взаимосвязь»), или корреляционная зависимость — статистическая взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.»
Наличие корреляции случайных величин лили автокорреляции) отнюдь не позволяет предсказать последующие значения случайной величины.
Kopilov
Хорошо, клякса с модификатором Mirror :D
N-Cube
Так вот этот объект гарантированно не случайный, а в статье выдается за таковой.
MagisterLudi
Этот пост — тоже «тест Роршаха». В чем то случайный, в чем-то специальный…
Каждый видит в нем то что захочет.
Вот вы увидели манипуляцию.
Кто-то ниже в комментах — козленка…
Красота в глазах смотрящего
N-Cube
Я за то, чтобы явно различать наглую ложь и статистику :) Несмотря на известное высказывание на эту тему, одно другому совсем не равноценно.
CorneliusAgrippa
Нет, это вы подразумеваете, что это просто случайная клякса. В тексте статьи четко написано, что это тест Роршаха. Определение теста Роршаха:
Где здесь откровенная ложь?
N-Cube
В статье утверждается, что в тесте Роршаха данные случайны, о том и речь.
Да, и само определение теста Роршаха тоже ложное, поскольку картинки теста немного не симметричны — ровно настолько, чтобы максимально походить на ту же бабочку. Как я выше указывал, коэффициент асимметрии эквивалентен таковому у реальной бабочки и практически невозможен для случайной кляксы. И это не все! Индекс фрактальности картинок теста соответствует таковому для живых объектов: Seeing shapes in seemingly random spatial patterns: Fractal analysis of Rorschach inkblots
anonymous
Делается случайная клякса, лист бумаги временно складывается образуя зеркальный отпечаток (вы можете видеть линию складывания, а противоположные картинки все-таки не полностью идентичны из-за неоднородностей структуры бумаги)
N-Cube
При складывании яркость отпечатка всегда меньше яркости оригинала, а здесь не так. Кроме того, в отпечатке могут появиться более темные пятна, но не более яркие — а на обсуждаемой картинке с обеих сторон можно найти более яркие области, то есть это не может быть отпечатком ни справа налево, ни слева направо. Далее, контуры на отпечатках уменьшаются — а тут даже мелкие элементы есть идентичные слева и справа.
anonymous
Все что вы назвали зависит от того насколько жидким краситель был во время складывания листа и времени выдержки в сложенном состоянии — можно получить полностью одинаковую экспозицию. Я почти уверен что использовались обычные акварельные краски в жидком виде — погуглите «кляксография».
Существуют и многоцветные пятна в исполнении Роршаха там еще больше угадывается данная техника.
N-Cube
Расскажите нам, как обычные акварельные краски могут отпечататься даже там, где их нет:

На картинке я отметил область, где есть пятно слева и нет пятна справа — с натяжкой, это мог бы быть отпечаток слева направо, но не справа налево. А еще область, где есть пятно справа и нет пятна слева — с натяжкой, это мог бы быть отпечаток справа налево, но не слева направо. Значит, вся картинка не может быть отпечатком ни слева направо, ни справа налево.
И да, полностью одинаковую экспозицию получить нельзя, поскольку проходит некоторое время до складывания, а скорость испарения пропорциональна концентрации чернил… Да тут еще уйма несоответствий, если приглядеться. Подсказка: я специализируюсь в оконных пространственных спектрах.
MagisterLudi
Кстати…

habr.com/ru/post/508770
N-Cube
Почему кстати, если симметрии тут вовсе нет (а есть несимметричная раскраска несимметрично свернутой змеи)? Мой первый комментарий относится к величине симметрии для бабочек и случайной кляксы и по этому показателю на картинке изображена бабочка, это легко посчитать и проверить.
alex103
.
.
.
и да… музей с камнями прикольный…