
Столкнувшись в университете с нейронными сетями, одной из любимых для меня стала именно сеть Хопфилда. Я был удивлен, что она оказалась последней в списке лабораторных, ведь ее работу можно наглядно продемонстрировать при помощи изображений и она не так сложна в реализации.
В этой статье продемонстрировано решение задачи восстановления искаженных изображений при помощи нейросети Хопфилда, предварительно обученной на эталонных изображениях.
Я постарался пошагово и как можно проще описать процесс реализации программы, позволяющей прямо в браузере поиграть с нейросетью, обучить сеть на собственноручно нарисованных образах и проверить её работу на искаженных образах.
Для реализации понадобится:
Браузер
Базовое понимание нейросетей
Базовые знания JavaScript / HTML
Немного теории
Нейронная сеть Хопфилда (англ. Hopfield network) — полносвязная нейронная сеть с симметричной матрицей связей. Такая сеть может быть использована для организации ассоциативной памяти, как фильтр, а также для решения некоторых задач оптимизации.
Сеть Хопфилда является абсолютно однородной структурой без какой-либо внутренней специализации ее нейронов. Её классический вариант состоит из единственного слоя нейронов, число которых является одновременно числом входов и выходов сети. Каждый нейрон сети связан со всеми остальными нейронами, а также имеет один вход, через который осуществляется ввод сигнала.
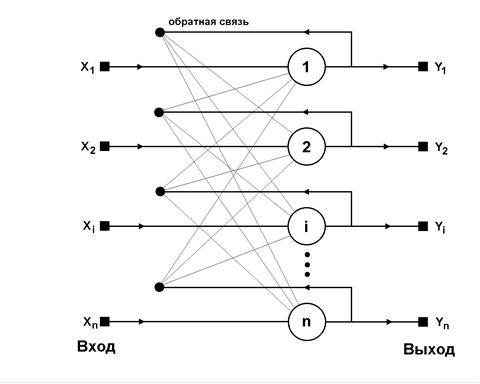
В общем виде задача, решаемая данной сетью в качестве ассоциативной памяти, формулируется следующим образом. Известен набор двоичных сигналов (например, изображений), которые считаются эталонными. Сеть должна уметь из произвольного искаженного сигнала, поданного на вход, «вспомнить» соответствующий эталонный образец (если такой есть).
Алгоритм работы сети:
Инициализация
Веса нейронов устанавливаются по следующей формуле:
где— количество образов
—
- ый и
- ый элементы вектора
- ого образца.
На входы сети подается неизвестный сигнал. Фактически его ввод осуществляется непосредственной установкой значений выходов:
Рассчитывается выход сети (новое состояние нейронов и новые значения выходов):
где— пороговая активационная функция с областью значений
;
— номер итерации;
— количество входов и нейронов.
Проверка изменения выходных значений за последнюю итерацию. Если выходы изменились — переход к пункту 3, иначе, если выходы стабилизировались, завершение функционирования. При этом выходной вектор представляет собой образец, наилучшим образом сочетающийся с входными данными.
Разработка
Визуальная часть
Для начала посмотрим как работает итоговый проект.
Он состоит из двух элементов Canvas и трех кнопок. Это простейший HTML и CSS код, не нуждающийся в пояснении (можете скопировать с гитхаба).
Левый элемент Canvas нужен для рисования изображений, которые затем будут использованы для обучения (кнопка Запомнить) или распознавания нейросети. На правом элементе отображается результат распознавания сигнала, находящегося на данный момент на левом Canvas (в данном случае сеть «вспомнила» букву Т на основе искаженного сигнала).
Здесь нужно обратить внимание на то, что область для рисования представлена сеткой 10?10 и позволяет закрашивать клетки только черным цветом. Так как в сети Хопфилда число нейронов равно числу входов, количество нейронов будет равно длине входного сигнала, то есть 100 (у нас всего 100 клеток на экране). Входной сигнал при этом будет двоичным — массив, состоящий из ?1 и 1, где ?1 — это белый, а 1 — черный цвет.
Наконец-то приступим к написанию кода, сначала инициализируем необходимые переменные.
Код инициализации
// Размер сетки установим равным 10 для простоты тестирования
const gridSize = 10;
// Размер одного квадрата в пикселях
const squareSize = 45;
// Размер входного сигнала (100)
const inputNodes = gridSize * gridSize;
// Массив для хранения текущего состояния картинки в левом канвасе,
// он же является входным сигналом сети
let userImageState = [];
// Для обработки движений мыши по канвасу
let isDrawing = false;
// Инициализация состояния
for (let i = 0; i < inputNodes; i += 1) {
userImageState[i] = -1;
}
// Получаем контекст канвасов:
const userCanvas = document.getElementById('userCanvas');
const userContext = userCanvas.getContext('2d');
const netCanvas = document.getElementById('netCanvas');
const netContext = netCanvas.getContext('2d');Реализуем функцию рисования сетки, используя инициализированные ранее переменные.
Функция отрисовки сетки
// Функция принимает контекст канваса и рисует
// сетку в 100 клеток (gridSize * gridSize)
const drawGrid = (ctx) => {
ctx.beginPath();
ctx.fillStyle = 'white';
ctx.lineWidth = 3;
ctx.strokeStyle = 'black';
for (let row = 0; row < gridSize; row += 1) {
for (let column = 0; column < gridSize; column += 1) {
const x = column * squareSize;
const y = row * squareSize;
ctx.rect(x, y, squareSize, squareSize);
ctx.fill();
ctx.stroke();
}
}
ctx.closePath();
};Чтобы «оживить» полученную сетку, добавим обработчики клика и движения мыши по канвасу.
Обработчики движений мыши
// Обработка клика мыши
const handleMouseDown = (e) => {
userContext.fillStyle = 'black';
// Рисуем залитый прямоугольник в позиции x, y
// размером squareSize х squareSize (45х45 пикселей)
userContext.fillRect(
Math.floor(e.offsetX / squareSize) * squareSize,
Math.floor(e.offsetY / squareSize) * squareSize,
squareSize, squareSize,
);
// На основе координат вычисляем индекс,
// необходимый для изменения состояния входного сигнала
const { clientX, clientY } = e;
const coords = getNewSquareCoords(userCanvas, clientX, clientY, squareSize);
const index = calcIndex(coords.x, coords.y, gridSize);
// Проверяем необходимо ли изменять этот элемент сигнала
if (isValidIndex(index, inputNodes) && userImageState[index] !== 1) {
userImageState[index] = 1;
}
// Изменяем состояние (для обработки движения мыши)
isDrawing = true;
};
// Обработка движения мыши по канвасу
const handleMouseMove = (e) => {
// Если не рисуем, т.е. не было клика мыши по канвасу, то выходим из функции
if (!isDrawing) return;
// Далее код, аналогичный функции handleMouseDown
// за исключением последней строки isDrawing = true;
userContext.fillStyle = 'black';
userContext.fillRect(
Math.floor(e.offsetX / squareSize) * squareSize,
Math.floor(e.offsetY / squareSize) * squareSize,
squareSize, squareSize,
);
const { clientX, clientY } = e;
const coords = getNewSquareCoords(userCanvas, clientX, clientY, squareSize);
const index = calcIndex(coords.x, coords.y, gridSize);
if (isValidIndex(index, inputNodes) && userImageState[index] !== 1) {
userImageState[index] = 1;
}
};Как вы могли заметить, обработчики использует некоторые вспомогательные функции, такие как getNewSquareCoords, calcIndex и isValidIndex. Ниже код этих функций с комментариями.
Вспомогательные функции
// Вычисляет индекс для изменения в массиве
// на основе координат и размера сетки
const calcIndex = (x, y, size) => x + y * size;
// Проверяет, помещается ли индекс в массив
const isValidIndex = (index, len) => index < len && index >= 0;
// Генерирует координаты для закрашивания клетки в пределах
// размера сетки, на выходе будут значения от 0 до 9
const getNewSquareCoords = (canvas, clientX, clientY, size) => {
const rect = canvas.getBoundingClientRect();
const x = Math.ceil((clientX - rect.left) / size) - 1;
const y = Math.ceil((clientY - rect.top) / size) - 1;
return { x, y };
};Далее напишем обработчик для кнопки Очистить. При нажатии на эту кнопку должны очищаться закрашенные квадраты двух кавасов и сбрасываться состояние входного сигнала.
Функция очистки сетки
const clearCurrentImage = () => {
// Чтобы убрать закрашенные клетки, просто заново отрисовываем
// всю сетку и сбрасываем массив входного сигнала
drawGrid(userContext);
drawGrid(netContext);
userImageState = new Array(gridSize * gridSize).fill(-1);
};Теперь можно переходить к разработке «мозга» программы.
Реализация алгоритма нейросети
Первый этап — инициализация сети. Добавим переменную для хранения значений весов нейронов и немного изменим цикл инициализации состояния изображения (входного сигнала).
Инициализация весов сети
...
const weights = []; // Массив весов сети
for (let i = 0; i < inputNodes; i += 1) {
weights[i] = new Array(inputNodes).fill(0); // Создаем пустой массив и заполняем его 0
userImageState[i] = -1;
}
...Так как каждый нейрон в сети Хопфилда связан со всеми остальными нейронами, веса сети представлены двумерным массивом, каждый элемент которого является одномерным массивом размером inputNodes элементов. В итоге мы получаем 100 нейронов, у каждого из которых по 100 связей.
Теперь реализуем обработку входного сигнала (изменение весов) нейросетью согласно формуле из первого шага алгоритма. Данный процесс происходит по нажатию на кнопку Запомнить. Запомненные образы будут является эталонами для последующего восстановления.
Код обработки входного сигнала
const memorizeImage = () => {
for (let i = 0; i < inputNodes; i += 1) {
for (let j = 0; j < inputNodes; j += 1) {
if (i === j) weights[i][j] = 0;
else {
// Напоминаю, что входной сигнал находится в массиве userImageState и является
// набором -1 и 1, где -1 - это белый, а 1 - черный цвет клеток на канвасе
weights[i][j] += userImageState[i] * userImageState[j];
}
}
}
};Запомнив один или более образов, можно попробовать подать на вход сети искаженный образ, либо сильно похожий на один из них, и попробовать распознать его. Напишем еще одну функцию:
Функция распознавания искаженного сигнала
// Где-то в html подключаем библиотеку lodash:
<script src="https://cdnjs.cloudflare.com/ajax/libs/lodash.js/4.17.21/lodash.min.js"></script>
...
const recognizeSignal = () => {
let prevNetState;
// На вход сети подается неизвестный сигнал. Фактически
// его ввод осуществляется непосредственной установкой значений выходов
// (2 шаг алгоритма), просто копируем массив входного сигнала
const currNetState = [...userImageState];
do {
// Копируем текущее состояние выходов,
// т.е. теперь оно становится предыдущим состоянием
prevNetState = [...currNetState];
// Рассчитываем выход сети согласно формуле 3 шага алгоритма
for (let i = 0; i < inputNodes; i += 1) {
let sum = 0;
for (let j = 0; j < inputNodes; j += 1) {
sum += weights[i][j] * prevNetState[j];
}
// Рассчитываем выход нейрона (пороговая ф-я активации)
currNetState[i] = sum >= 0 ? 1 : -1;
}
// Проверка изменения выходов за последнюю итерацию
// Сравниваем массивы при помощи ф-ии isEqual
} while (!_.isEqual(currNetState, prevNetState));
// Если выходы стабилизировались (не изменились), отрисовываем восстановленный образ
drawImageFromArray(currNetState, netContext);
};Здесь для сравнения выходов сети на предыдущем и текущем шаге используется функция isEqual из библиотеки lodash.
Для отрисовки полученного сигнала используется функция drawImageFromArray. Она преобразует выходной сигнал сети в двумерный массив и отрисовывает его на правом канвасе.
Функция отрисовки изображения из массива точек
const drawImageFromArray = (data, ctx) => {
const twoDimData = [];
// Преобразуем одномерный массив в двумерный
while (data.length) twoDimData.push(data.splice(0, gridSize));
// Предварительно очищаем сетку
drawGrid(ctx);
// Рисуем изображение по координатам (индексам массива)
for (let i = 0; i < gridSize; i += 1) {
for (let j = 0; j < gridSize; j += 1) {
if (twoDimData[i][j] === 1) {
ctx.fillStyle = 'black';
ctx.fillRect((j * squareSize), (i * squareSize), squareSize, squareSize);
}
}
}
};Финальные приготовления
Для полноценного запуска программы осталось только добавить наши функции в качестве обработчиков для элементов HTML и вызвать функции отрисовки сетки.
Привязываем функции к HTML элементам
const resetButton = document.getElementById('resetButton');
const memoryButton = document.getElementById('memoryButton');
const recognizeButton = document.getElementById('recognizeButton');
// Вешаем слушатели на кнопки
resetButton.addEventListener('click', () => clearCurrentImage());
memoryButton.addEventListener('click', () => memorizeImage());
recognizeButton.addEventListener('click', () => recognizeSignal());
// Вешаем слушатели на канвасы
userCanvas.addEventListener('mousedown', (e) => handleMouseDown(e));
userCanvas.addEventListener('mousemove', (e) => handleMouseMove(e));
// Перестаем рисовать, если кнопка мыши отпущена или вышла за пределы канваса
userCanvas.addEventListener('mouseup', () => isDrawing = false);
userCanvas.addEventListener('mouseleave', () => isDrawing = false);
// Отрисовываем сетку
drawGrid(userContext);
drawGrid(netContext);Демонстрация работы нейросети
Обучим сеть двум ключевым образам, буквам Т и Н:

Теперь проверим работу сети на искаженных образах:
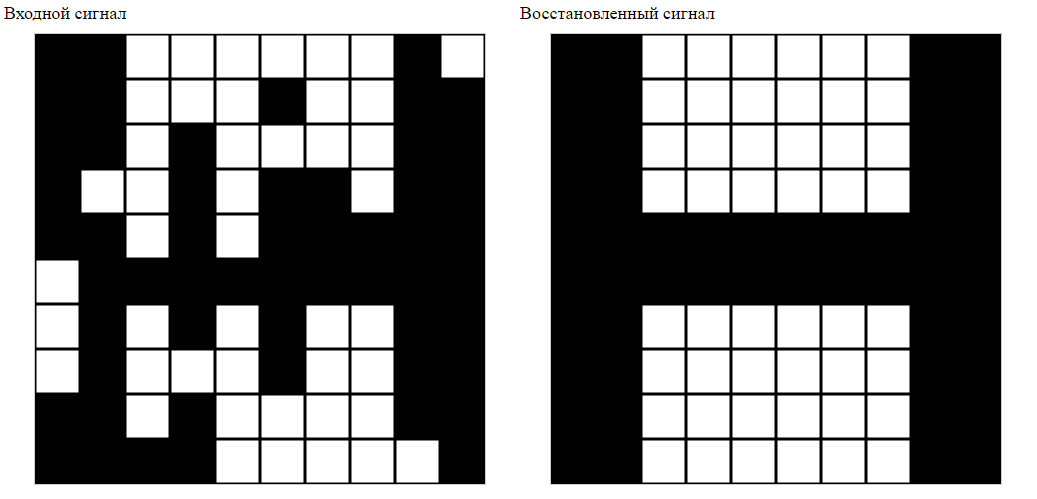

Программа работает! Сеть успешно восстановила исходные образы.
В заключение стоит отметить, что для сети Хопфилда число запоминаемых образов не должно превышать величины, примерно равной
(где
— размерность входного сигнала и количество нейронов). Кроме того, если образы имеют сильное сходство, то они, возможно, будут вызывать у сети перекрестные ассоциации, то есть предъявление на входы сети вектора А приведет к появлению на ее выходах вектора Б и наоборот.
Вместо литературы использовались лекции отличного преподавателя по нейронным сетям — Рощина Сергея Михайловича, за что ему большое спасибо.


bugs_eliminator
На мой взгляд, легкая для чтения получилась публикация, объясняющая чайнику как работает конкретный вид нейросетей. Однозначно — в закладки.
Подкупило наличие простых формул и что демо изготовлено как лабораторный стенд, можно неторопливо потыкать кнопки, вникая в сложную тему. А простой исходный код на Javascript — за это отдельное спасибо!
Кстати, похожие эксперименты проводились когда-то в Украине. Сеть из 21 программного нейрона училась распознавать цифры с экрана размером 10х10 на почве нескольких эпох обучения. Каждая эпоха совершалась экспериментатором вручную, наводя курсор мыши на образец цифры, нажимая кнопку запоминания, после чего сеть распознавала еще и измененные варианты цифры.
Но было это 19 лет назад, сайт тот уже не существует (ниже будут ссылки, которые нашел в истории web.archive.org по тем экспериментам). Вопросом нейросетей интересовались в 2002-2003 годах единицы, в основной в научной среде, что объясняет демонстрацию на Delphi.
Ваш пример на Javascript современней, а исходный код можно поковырять самостоятельно, увидеть результат изменений на экране браузера немедленно, чего не скажешь о примере на Delphi. Так что респект, автор!
Теперь ссылки (учтите, web.archive.org недоступен сейчас с российских IP-адресов, скорее всего по причине блокировки их домена):
Эксперимент N1: простое распознавание образов
Эксперимент N2: распознавание искаженных образов
Эксперимент N3: реакция на раздражение
soanyway Автор
Спасибо, приятно получить такой развёрнутый отзыв на первую публикацию!
На досуге обязательно ознакомлюсь с приведёнными экспериментами.
Именно это и было основной целью статьи.
P.S. web.archive.org вроде бы уже давно разблокирован, у меня свободно открывается.