Конденсатор имеет следующее схематическое изображение

Рассмотрим водопроводную модель конденсатора. Ранее мы говорили о том, что ток может течь только в трубе, соединенной в кольцо в замкнутой цепи. Но можно представить пустую емкость, в которую можно заливать воду, пока емкость не заполнится. Это и есть конденсатор — емкость, в которую можно заливать заряд.

Для большей аналогии лучше представить себе водонапорную башню, в модели - трубу бесконечной длины поставленную вертикально. Вода насосом закачивается в эту трубу с нижнего торца и поднимается на высоту. Чем больше воды закачали и чем выше она поднялась - тем сильнее столб воды давит на днище и выше там давление. Так-то в эту бесконечную трубу можно сколько угодно воды (электрического заряда) закачать, но при этом противодавление столба воды будет расти. Если качать заряд генератором напряжения, то когда противодавление сравняется с давлением (напряжением), создаваемым генератором - закачка остановится.

Если характеристикой резистора является сопротивление, то электрической характеристикой конденсатора является емкость.

С=Q/U

Емкость говорит, сколько заряда можно в конденсатор закачать, чтобы напряжение там поднялось до величины U. Можно сказать, что емкость характеризует диаметр трубы. Чем yже труба, тем быстрее поднимается уровень воды при закачке и растет давление на дне трубы. Давление же зависит только от высоты водяного столба, а не от массы закачанной воды.

В электрических терминах, чем меньше емкость конденсатора, тем быстрее растет напряжение при закачке туда заряда.

Напомню, что электрический ток I равен количеству протекающего заряда Q в секунду. То есть I=Q/T, где T - время. Это все равно, что поток воды исчисляемый кубометрами в секунду. Или килограммами в сек, потом проверим по размерности).

Поэтому конденсатор с маленькой емкостью заполняется зарядом быстро, а с большой емкостью - медленно.

Рассмотрим теперь электрические цепи с конденсатором.

Пусть конденсатор подключен к генератору напряжения.

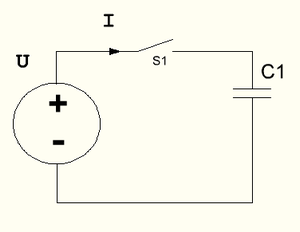
"Главный инженер повернул рубильник" S1 и.. тыдыщ!!! Что произошло?

Идеальный генератор напряжения имеет бесконечную мощность и может выдавать бесконечный ток. Когда замкнули рубильник в нашу емкость хлынуло бесконечное количество заряда в секунду и она мгновенно заполнилась и напряжение на ней выросло до U.

Теперь рассмотрим более реальную цепь.

Это Вторая Главная Цепь в жизни инженера-электронщика (после делителя напряжения) —
RC–цепочка.

RC–цепочка

RC -цепочки бывают интегрирующего и дифференцирующего типа.

RC–цепочка интегрирующего типа

Что произойдет в этой схеме, если замкнуть выключатель S1?

Конденсатор С исходно разряжен и напряжение на нем рано 0. Поэтому ток в первый момент будет равен I=U/R. Затем конденсатор начнет заряжаться, напряжение на нем увеличивается, и ток через резистор начнет уменьшаться. I=(U-Uc)/R. Этот процесс будет продолжаться, конденсатор будет заряжаться уменьшающимся током до напряжения источника U. Напряжение на конденсаторе при этом будет расти по экспоненте.

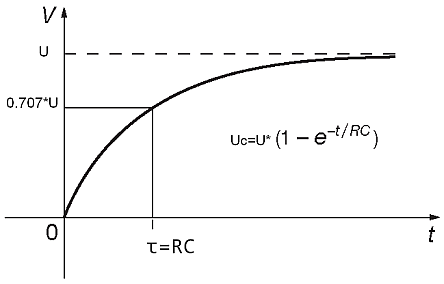
Вопрос: А если запитать такую цепочку от генератора тока, как будет расти напряжение на конденсаторе?

Почему цепочка называется - «интегрирующего типа»?

Как выше было отмечено, ток в первый момент после подачи напряжение будет равен I=U/R, так как конденсатор разряжен, и напряжение на нем равно 0. И какое-то время, пока напряжение на конденсаторе Uc мало по сравнению с U, ток будет оставаться почти постоянным. А при заряде конденсатора постоянным током напряжение на нем растет линейно.

Uc=Q/C, а мы помним, что ток это количество заряда в секунду, то есть скорость протекания заряда. Другими словами, заряд это интеграл от тока.

Q = ? I * dt =? U/R * dt

то есть

Uc=1/RC * ? U * dt

Но все это близко к истине в начальный момент, пока напряжение на конденсаторе малo.

На самом деле все сводится к тому, что конденсатор заряжается постоянным током.
А постоянный ток выдает генератор тока. (См. вопрос выше)
Если источник напряжения выдает бесконечно большое напряжение и сопротивление R также имеет бесконечно большую величину, то по факту мы имеем уже идеальный генератор тока, и внешние цепи на величину этого тока влияния не оказывают.

RC–цепочка дифференцирующего типа

Ну тут все то же самое, что в интегрирующей цепочке, только наоборот.

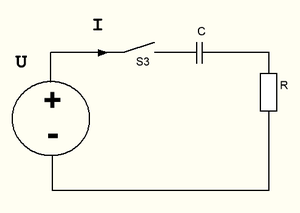
Более подробно свойства RC цепей хорошо освещены в интернете.

Параллельное и последовательное соединение конденсаторов

Так же как резисторы, конденсаторы можно соединять последовательно и параллельно.

При параллельном соединении емкости складываются - ну это и понятно, это как заполнять сообщающиеся сосуды, общий объем получается равным сумме объемов. При последовательном же соединении получится так, что конденсатор с маленькой емкостью заполнится зарядом быстрее, чем конденсатор с большой емкостью. Напряжение на маленьком конденсаторе быстро вырастет почти до напряжения источника ( ну и остальные конденсаторы внесут свой вклад) , ток в общей цепи уменьшится до нуля, и процесс заряда конденсаторов прекратится. Таким образом емкость последовательно соединенных конденсаторов получается меньше емкости самого маленького из них.

Upd.
Рассмотрим более подробно процесс заряда конденсатора на схеме рис.10 (по мотивам учебника И.В.Савельева "Курс общей физики", том II. "Электричество" )
Как было сказано в предыдущей статье О природе электрического тока электрический ток - это движение заряженных частиц. В проводниках ( в отличие от диэлектриков-изоляторов) часть электронов является свободными и такие электроны могут перескакивать от одного атому к другому. В целом проводник электрически нейтрален - отрицательный заряд электронов компенсируется положительным зарядом ядер атомов. Чтобы заставить электроны двигаться нужно создать их избыток на одном конце проводника и недостаток на другом. Этот избыток электронов на одном полюсе создает батарейка вследствие протекающих в ней электрохимических реакций. Когда проводник присоединяется к полюсам батарейки электроны от полюса, где их избыток начинают двигаться к другому полюсу, потому что одноименные заряды отталкивают друг друга. Эти свободные электроны движутся внутри проводника по всему объему.
Движение электронов в RC цепи на рис. 3 имеет другой характер. Поскольку цепь не замкнута (обкладки конденсатора не соединены друг с другом) постоянный ток в цепи идти не может. Поэтому поступающий избыток электронов с полюса батарейки приводит к тому, что проводник теряет электрическую нейтральность. Избыточный заряд q, распределяется по поверхности проводника так, чтобы напряженность поля внутри проводника была равна нулю. Ну это понятно, одноименные заряды отталкиваются и стремятся расположиться подальше друг от друга, то есть на поверхности. Если бы не было резистора R, то перераспределение зарядов по поверхности происходило бы мгновенно. Однако резистор ограничивает ток ( движение зарядов) поэтому перераспределение происходит постепенно. По мере зарядки конденсатора напряжение на нем растет и ток через резистор уменьшается. Избыточные электроны концентрируются на одной обкладке и создают электрическое поле. Это поле отталкивает электроны, находящиеся на другой обкладке и "проталкивает" их дальше по проводнику к отрицательному полюсу батареи. (Знаки + и - в данном случае берем условно). Таким образом в незамкнутой цепи протекает ток заряда конденсатора. Этот ток не постоянный и уменьшается со временем. Однако, если в какой-то момент поменять полярность батареи, то ток потечет уже в обратную сторону. Если это переключение делать достаточно часто, так чтобы конденсатор не успевал полностью зарядиться, то в цепи все время будет течь ток, то в одну, то в другую сторону. Это и происходит, когда говорят, что "конденсатор проводит переменный ток".
Для плоского конденсатора емкость равна С=?0*?*S/d , где d – зазор между обкладками, ? – диэлектрическая проницаемость вещества, заполняющего зазор, S - площадь обкладок.
То есть на емкость влияет не только площадь обкладок и расстояние между ними, но и материал диэлектрика, который между обкладками помещен. Причем на емкость конденсатора материал диэлектрика может влиять достаточно сильно, с разными дополнительными эффектами, см. например статью "Поляризация диэлектрика"

Литература
"Драма идей в познании природы", Зельдович Я.Б., Хлопов М.Ю., 1988
"Курс общей физики", том II. "Электричество" И.В.Савельев
Википедия - статьи про электричество.