Автор: Сергей Тимофеев, программист-разработчик, Игорь Батюченко, руководитель группы разработки, ЗАО «Топ Системы»
В статье рассматривается теоретическая основа работы обновлённых команд создания спиральной кривой и спирали в T-FLEX CAD 17.
Введение
Спирали различных форм встречаются в технике, архитектуре, быту и природе, например, раковины морских животных или молекулы ДНК (рис.1). Глобально их можно разделить на два типа: плоские и трёхмерные. Плоские спирали более интересны в плане науки, однако в технике чаще встречаются трёхмерные (как частный случай — пружины). По этой причине рассмотрим особенности построения именно трёхмерных спиралей и разберёмся с какими трудностями можно столкнуться в процессе работы.
В T-FLEX CAD 17 в команды создания спиральной кривой и спирали был внесён ряд улучшений. Они затронули интерфейс ввода исходных данных, а также генерацию результирующих кривых и тел. Благодаря этим изменениям, команды Спиральный путь и Спираль теперь имеют схожий эргономический пользовательский интерфейс. Команды также получили новые инструменты управления формой спиралей, а кроме того, были повышены точность и производительность построения геометрии.
Команда Спиральный путь
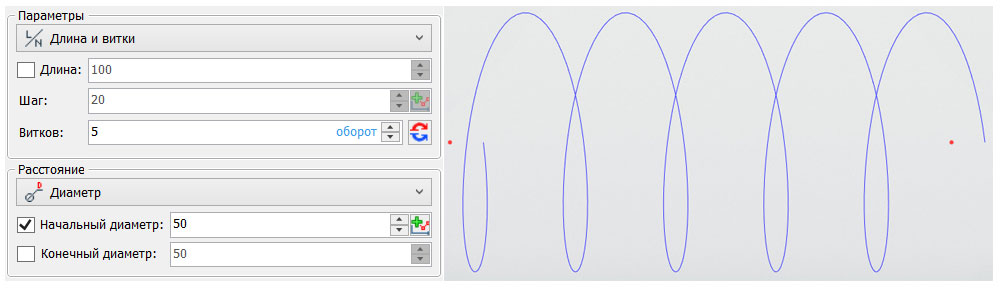
Для создания спиральной кривой (проволочного тела) самой простой и общей формы, необходимы следующие исходные данные: ось, диаметр, значения двух из трёх параметров (длина, шаг, количество витков), определяющие габариты и периодичность витков. Тогда спиральный путь можно получить в виде сплайна, построив его по заранее рассчитанному массиву точек. Также можно написать функцию по расчёту координат будущих точек и производных в данном положении. В любом случае даже на основании исходных данных можно понять, какой результат должен получиться в итоге (рис. 2).
Но что, если в качестве оси для будущего спирального пути нужно использовать не прямой отрезок, а кривую (или набор кривых) произвольной формы? Это могут быть кривые как второго порядка (аналитические кривые: парабола, гипербола, дуга окружности или эллипса), так и более высоких порядков (сплайн). В таком случае математическая сложность вычисления положения и количества опорных точек спиральной кривой вдоль осевой направляющей существенно влияет как на точность результирующей кривой, так и на производительность алгоритма построения. В связи с этим в T-FLEX CAD 17 используется альтернативный способ построения геометрии: на основе двумерной кривой и несущей поверхности.
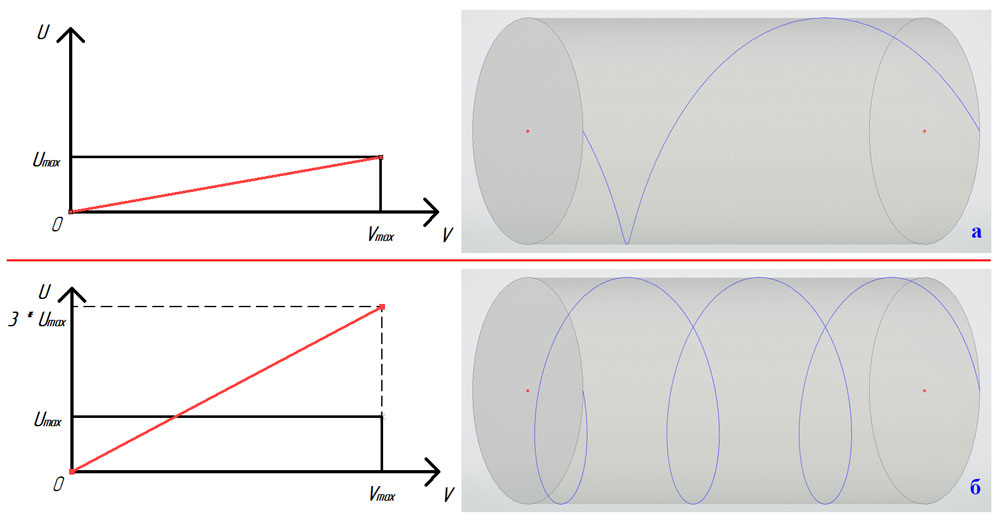
Возвращаясь к базовому примеру спиральной кривой (рис. 2), можно заметить, что она лежит на «воображаемой» цилиндрической поверхности (рис. 3). Каждая точка кривой, определяемая параметром t, соответствует конкретной точке на поверхности, совпадающей в трёхмерном пространстве и определяемой параметрами U и V. Таким образом, если мы сначала создадим цилиндрическую поверхность заданного диаметра, а затем в двумерном пространстве этой поверхности построим линию по двум точкам, соответствующим минимальным и максимальным значениям U и V, то в трёхмерном пространстве получим спиральный путь в один виток (рис. 4 сверху). Совокупность двумерной кривой (построенной в пространстве UV-параметров) и поверхности называется Кривая на поверхности.
Для спиральной кривой с несколькими витками справедлив тот факт, что по «ширине» данная поверхность является замкнутой и периодической. В этом случае при построении двумерной кривой в UV-пространстве нужно умножить необходимое количество витков на максимальное значение параметра, определяющего «ширину» поверхности (то есть на период) (рис. 4 снизу).
Если в качестве оси будет не отрезок прямой, а набор гладкосопряжённых произвольных кривых, то по такому осевому пути не получится построить цилиндрическую поверхность. Тем не менее подобный подход работает не только для цилиндрической, но и для любых циклических поверхностей (цилиндрическая поверхность лишь частный случай). Более того, если есть необходимость задания переменного диаметра по длине, то учитывать его нужно именно на этапе построения поверхности. Но в данном случае уже нельзя строить двумерную кривую в виде отрезка прямой по двум точкам. Необходимо учитывать (возможную) неравномерную параметризацию несущей сплайновой поверхности. В противном случае распределение витков по длине оси будет непропорциональным (шаг между витками будет непостоянным). Таким образом, получив массив двумерных точек в UV-координатах и построив по нему сплайн, можно получить спиральную кривую вдоль любой произвольной осевой направляющей (рис. 5).
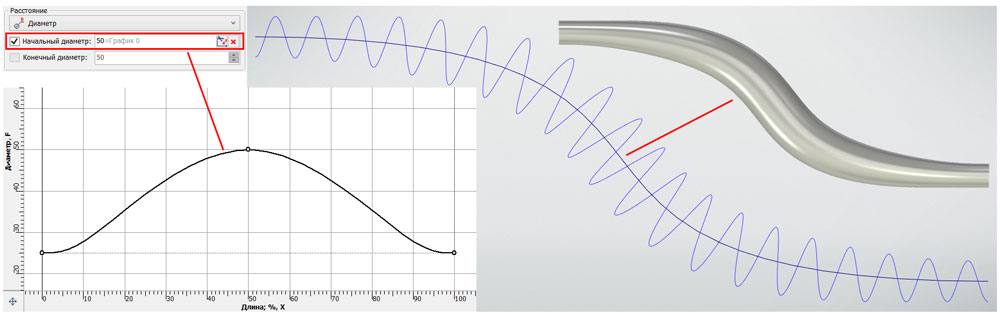
Рис.5. Спиральный путь вдоль оси в виде сплайна с переменным диаметром
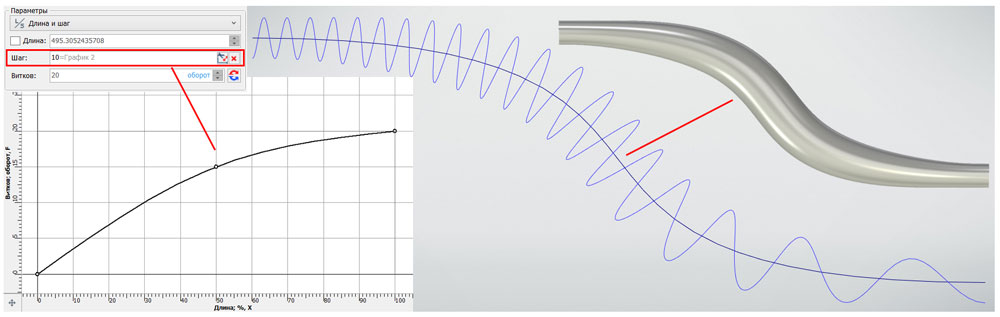
При необходимости, можно подключить и закон изменения шага витков вдоль направляющей осевой кривой. В данном случае, не зависимо от типа поверхности, которую мы получили, нужно рассчитать массив точек в UV-координатах. На каждое значение координаты, отвечающей за «длину» (чаще всего это параметр V), у нас будет заданное количество витков, умноженное на период поверхности, то есть «ширина» (чаще всего это параметр U). Таким образом, имея в арсенале три перечисленные возможности: произвольные (в том числе замкнутые) осевые направляющие, переменный диаметр и переменный шаг, можно создавать спиральные кривые различного типа и формы (рис. 6, 7).

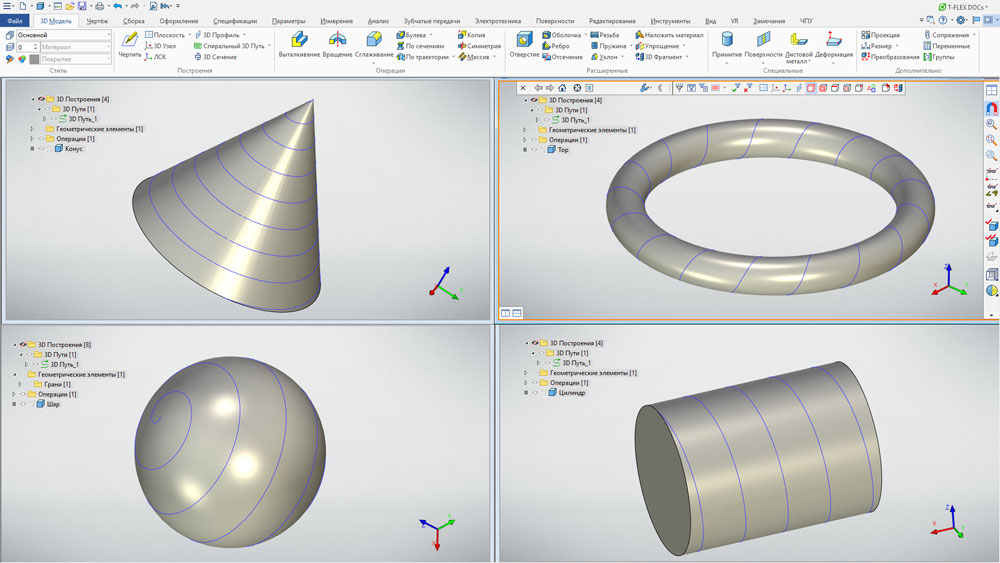
Если в модели уже существует циклическая поверхность, по которой нужно построить спиральную кривую, то описанный алгоритм сработает и в данном случае. Кривая будет создана на основе несущей поверхности выбранной грани, без создания вспомогательной геометрии (рис. 8). Такой подход позволяет создавать различные спиральные кривые (рис.9). При этом можно гарантировать, что они будут полностью принадлежать выбранной грани (поверхности). В свою очередь это позволит использовать команду По траектории, зафиксировав кручение профиля вдоль всей длины осевой направляющей (об этом далее).
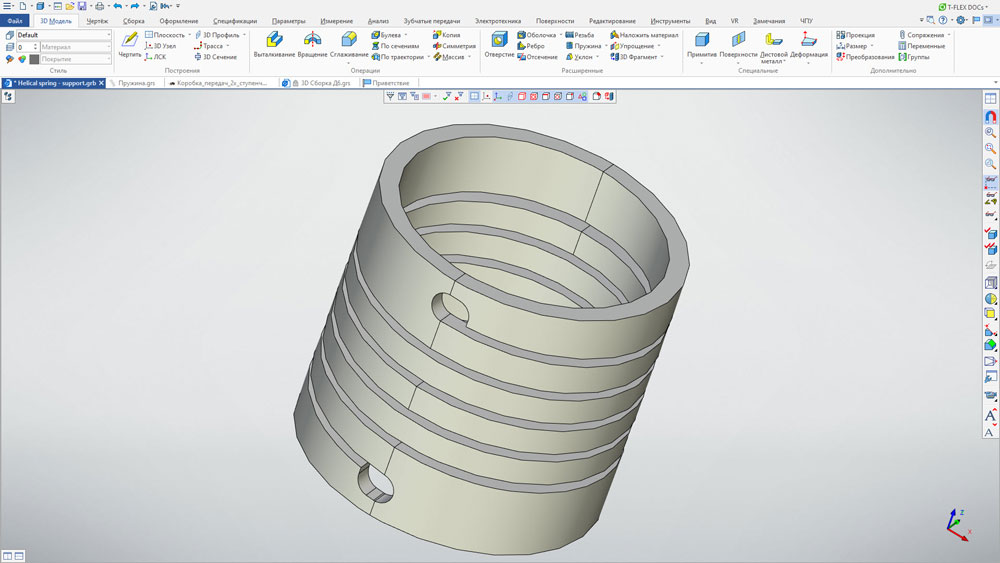
Операция Спираль
Создание спирали (твердого тела) является логичным продолжением создания спирального пути, о котором говорилось ранее. Для получения результирующего тела желаемой формы можно воспользоваться командой «По траектории» и просто «протолкнуть» выбранный профиль вдоль заранее созданной спиральной кривой, которая в данном случае и будет траекторией. Однако в результате можно увидеть, что профиль начинает «крутить», и чем дальше мы продвигаемся вдоль оси, тем более заметно отклонение от исходной ориентации. На рисунке 10а видно, что грань, подсвеченная синим цветом, представляет собой внутренний габарит спирали в начале оси, но в конце она становится внешним габаритом.
Управлять кручением профиля поможет несущая поверхность, которая создаётся в спиральной кривой. В каждой точке траектории дополнительно вычисляется нормаль поверхности в данной позиции. Таким образом, можно «зафиксировать» исходное положение профиля и сохранить его ориентацию на всём протяжении вдоль осевой направляющей. В итоге алгоритм создания спирали сводится к следующему:
создаётся спиральная кривая, у которой в свою очередь создаётся поверхность, которой эта кривая и принадлежит («кривая на поверхности»);
выбранный профиль протягивается вдоль этой кривой, с учётом несущей поверхности;
сама кривая и её поверхность остаются невидимыми для пользователя.
В результате на рисунке 10б видно, что профиль не меняет свою ориентацию на всём протяжении вдоль осевой направляющей спирали.

К описанным ранее возможностям Спирального пути (произвольный осевой путь, график диаметра и переменного шага) в команде Спираль можно добавить график переменного масштаба исходного профиля. Это может потребоваться, например, при моделировании резьбы на горлышке бутылки (рис. 11, 12).

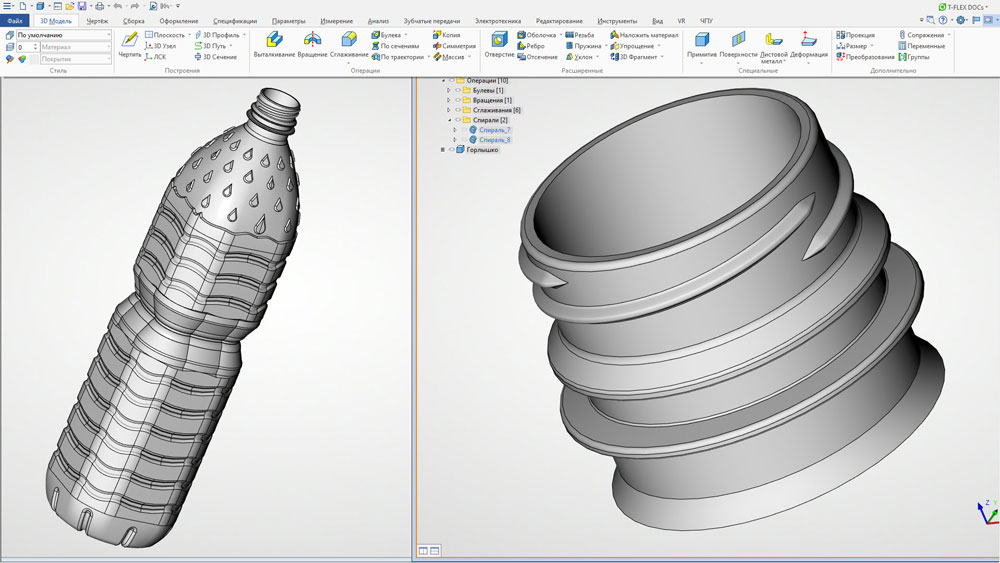
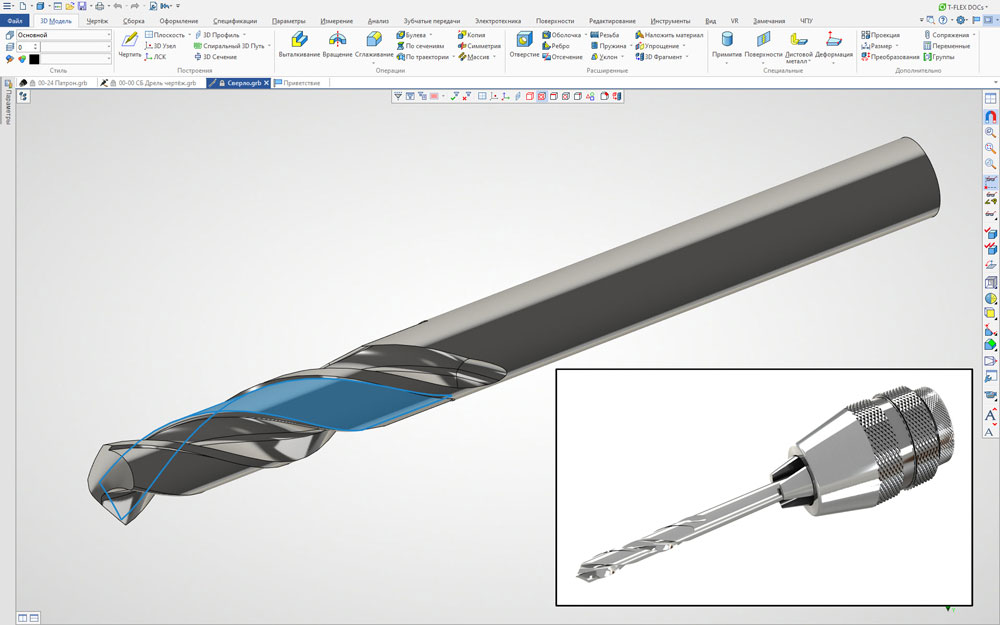
На рисунке 13 показан практический пример моделирования спиралей в реальных технических изделиях.

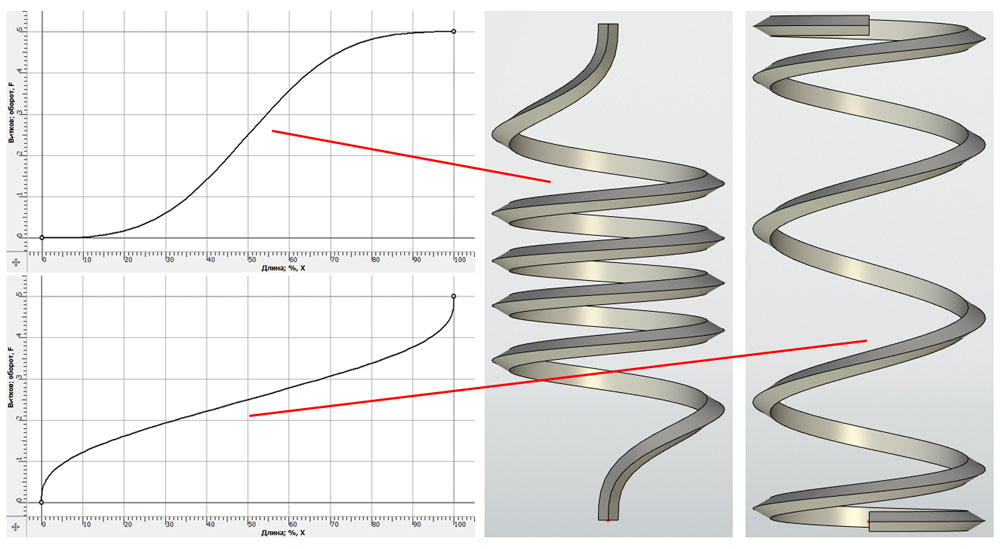
В графике переменного шага, заданного как Кубический сплайн, учитываются касательные условия для крайних точек. При задании соответствующих условий можно получить спирали, показанные на рисунке 14.
Заключение
Алгоритм генерации на базе «кривой на поверхности» позволяет создавать геометрию с высокой точностью и большой производительностью, будь то проволочные тела (спиральный путь) или твердотельные операции (спираль)(рис.15). Также он позволяет создавать операции вдоль произвольных осевых направляющих. А возможность использования графиков для переменного диаметра, шага и масштаба делает обновлённые команды более функциональными, практически полностью закрывающими спектр требований конструкторов при работе со спиральными телами.