Коллапсирующие CNN: аппроксимация, имитация и щепотка спектральной магии / forpes.ru

Главная
Коллапсирующие CNN: аппроксимация, имитация и щепотка спектральной магии

Коллапсирующие CNN: аппроксимация, имитация и щепотка спектральной магии +8

16.06.2022 16:31

neuro_diletant 3 1300 Источник

Можно ли ускорить обученную сверточную нейросеть? Можно ли заметно сократить ее веса, не снижая точности? Можно ли найти и «обезвредить» узкие места в модели, препятствующие достижению максимальной точности? Можно ли радикально изменить архитектуру готовой сетки, не прибегая к обучению с нуля?

А вот и посмотрим.

Сначала о производительности

Сверточные нейросети хороши всем, кроме объема вычислений. Можно представить такую сеть как стопку изображений со все меньшим числом пикселей, где значением одного пикселя самого верхнего слоя является тройка цветов RGB, преобразуемая от слоя к слою в вектор т.н. признаков все большей размерности. В конце остается самая маленькая матрица из самых длинных векторов. Которые чаще всего поэлементно усредняются к единственному выходному вектору, и затем уже следует одно-двухслойный перцептрон классификатора.

Преобразование данных в сверточной нейросети

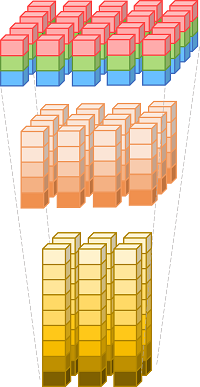
Чтобы получить значение одного выхода в одном пикселе слоя нужно скомбинировать вектора признаков всех соседних пикселей предыдущего слоя. Это десятки, сотни, а иногда и тысячи умножений и сложений. Учитываем количество выходов в пикселе, количество пикселей в слое, количество слоев, - и легко получаем по 100-200 миллионов операций даже на самых компактных моделях со скромными 2М весов (солидные содержат в 10-30 раз больше).

Предлагались разные варианты борьбы с этой проблемой, в том числе групповая свертка. Можно разбить признаки (каналы) слоя на несколько групп небольшой размерности, и провести автономную свертку внутри каждой группы, а затем как-нибудь скомбинировать или просто перемешать каналы между группами. (Так устроена, например, ShuffleNet). Но более успешной оказалась архитектура с группами размером в один единственный канал (т.н. depthwise separable convolution).

Одним из типичных представителей этого многочисленного семейства моделей является вариация MobileNet v3 от Google, состоящая из весьма однотипных строительных блоков. Не вдаваясь в детали, каждый блок можно упрощенно представить в виде набора следующих слоев:

1) слой расширения, увеличивающий входные каналы одного пикселя в несколько раз;

2) слой одноканальной свертки 3x3 или 5x5, передающий информацию между соседними пикселями раздельно для каждого из возросшего числа признаков;

3) слой сжатия, обратно уменьшающий каналы внутри пикселя до разумного минимума.

Как следует из названия, эта модель призвана обеспечить приемлемый баланс между точностью и объемом расчетов в средах с умеренными вычислительными возможностями. Но даже здесь, если присмотреться, основная нагрузка приходится на первый и последний слои блока (которые реализуются в виде свертки с ядром 1x1, т.е. простого перцептрона, миксирующего заданное число входов в необходимое количество выходов). Можно ли еще здесь как-нибудь сэкономить?

Осторожный оптимизм внушает такое свойство нейросетей как избыточность. Можно наугад обнулить десятки, сотни, или даже тысячи весов сколько-нибудь сложной сетки, и ничего заметного не произойдет. Так устроен один из эффективных методов повысить точность при обучении, - прореживание (dropout). Случайным образом временно отключаются 10-30% входов слоя, т.е. локально купируется избыточность, и точность предсказания ощутимо повышается, т.к. слой вынужден искать приемлемые варианты даже в условиях дефицита входящей информации.

Выборочное прореживание

Рассмотрим самый базовый перцептрон с несколькими входами и всего одним выходом. Когда требуется больше выходов, такие элементарные конструкции просто объединяются в стек. Функция активации нас не интересует, - часто она выделяется в отдельный слой, следующий после пакетной нормализации (BatсhNorm) выходов свертки.

$y=\sum_{i}{W_{i}x_{i}}+b$

C целью оптимизации можно попробовать отказаться от нескольких входов, которые имеют самое незначительное влияние на результат, т.е. с самыми маленькими по модулю весами $|W_{i}|$ . Веса в слое могут отличаться на 2-3 порядка, - есть из чего выбрать. В терминах свертки это эквивалентно умножению входящего плотного тензора значений на разреженную матрицу весов.

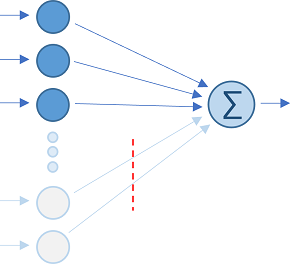
Итак, мы можем произвести осмысленное стационарное прореживание, связывающее с каждым выходом свой персональный набор входов, руководствуясь масштабом предварительно обученных весов. Есть еще варианты?

Пожалуй да. Вместо выставления за дверь неугодного канала, можно попробовать заменить его на константу, - матожидание данного входа. Произведение $W_{i}\overline{x}_{i}$ пополнит смещение а дальше мы получаем предыдущий вариант. Мы уже не просто отбросили вход, но сохранили часть информации о нем в выходе.

Не останавливаемся на достигнутом! Пусть $x=\sigma n+\overline{x}$ , где - центрированная величина с единичным отклонением. Тогда вклад одного канала в можно записать как $s_{i}=W_{i}\sigma_{i}n_{i}+W_{i}\overline{x}_{i}$ Т.е., оставляя только матожидание входа, мы выбрасываем осцилляцию $W_{i}\sigma_{i}n_{i}$ что вносит среднюю ошибку порядка $e = | W_{i} \sigma_{i} |$

Очевидно, для минимизации такой ошибки мы должны выбрать кандидатов на удаление с самыми скромными $|W_{i}\sigma_{i}|$ а не просто $|W_{i}|$

Межканальная корреляция

Посмотрим, что будет, если не выбрасывать $n_{i}$ , а заменить на единичную осцилляцию другого канала. Если они заметно коррелируют, то результат может оказаться интересным. Как известно, дисперсия суммы

$D(x_{1}+x_{2})=Dx_{1}+Dx_{2}+2\mathrm{cov}(x_{1},x_{2})$

Если принять $n_{i}=an_{j}+\varepsilon_{ij}$ то

$D(\varepsilon_{ij})=D(n_{i}-an_{j})=1+a^{2}-2ar_{ij}$

где $r_{ij}$ - линейный коэффициент корреляции между исходными каналами $x_{i}$ и $x_{j}$ Это парабола с минимумом при $a=r_{ij}$ Т.е. подстановка должна быть $n_{i}=r_{ij}n_{j}+\varepsilon_{ij}$

Тогда среднеквадратичное отклонение довеска $\varepsilon_{ij}$ составит

$\sigma_{\varepsilon}=\sqrt{1-r_{ij}^{2}}$

Т.к.

$W_{i}\sigma_{i}n_{i}=W_{i}\sigma_{i}r_{ij}n_{j}+W_{i}\sigma_{i}\varepsilon_{ij}=W_{i}\sigma_{i}r_{ij}\frac{x_{j}-\overline{x}_{j}}{\sigma_{j}}+W_{i}\sigma_{i}\varepsilon_{ij}$

то очевидно, при замене теряется член $W_{i}\sigma_{i}\varepsilon_{ij}$ который имеет оценку

$e_{ij}=|W_{i}|\sigma_{i}\sigma_{\varepsilon}=|W_{i}|\sigma_{i}\sqrt{1-r_{ij}^{2}}$

Что означает гарантированный выигрыш при заметной корреляции между входами, и чем она больше, тем лучше. При этом меняется не только bias, но и вес канала-«спонсора»:

$W_{j}^{'}=W_{j}+\frac{W_{i}\sigma_{i}r_{ij}}{\sigma_{j}}, b^{'}=b+W_{i}\overline{x}_{i}-\frac{W_{i}\sigma_{i}r_{ij}\overline{x}_{j}}{\sigma_{j}}$

Стратегия выбора входов-аутсайдеров тоже меняется: подбираем каналы с минимальной $e_{ij}$

Полная аппроксимация

Попробуем выразить суммарную осцилляцию второстепенных входов (хвост) через композицию остающихся основных каналов (ядро).

Условимся обозначать переменные ядра индексами i и j, а переменные хвоста – индексом k. Т.е.,

$y=\sum_{i}W_{i}x_{i}+\sum_{k}W_{k}x_{k}+b=\sum_{i}W_{i}x_{i}+\sum_{k}W_{k}(\sigma_{k}n_{k}+\overline{x}_{k})+b$

Представим

$\sum_{k}W_{k}\sigma_{k}n_{k}=\sum_{i}a_{i}n_{i}+\varepsilon$

Наша цель, - подобрать $a_{i}$ так, чтобы погрешность $\varepsilon$ была минимальной. Воспользуемся формулой

$D(\sum_{i}x_{i})=\sum_{i}Dx_{i}+\sum_{i\neq j}\mathrm{cov}(x_{i},x_{j})$

Тогда, обозначив $W_{k}\sigma_{k}=\omega_{k}$ получим

$D\varepsilon=D(\sum_{k}\omega_{k}n_{k}-\sum_{i}a_{i}n_{i})=\\\sum_{k}\omega_{k}^{2}+\sum_{k\neq l}\omega_{k}\omega_{l}r_{kl}+\sum_{i}a_{i}^{2}+\sum_{i\neq j}a_{i}a_{j}r_{ij}-2\sum_{k,i}\omega_{k}a_{i}r_{ki}$

Первые две пары слагаемых во второй строке — это дисперсии хвоста и его аппроксимации, а последняя сумма – ковариация между ними. Относительно каждого $a_{i}$ снова имеем параболу с минимумом при

$a_{i}=\sum_{k}\omega_{k}r_{ki}-\sum_{i\neq j}a_{j}r_{ij}$

(Здесь учтено, что слагаемые $a_{i}a_{j}r_{ij}$ в силу симметричности повторяются дважды). Т.е. мы получаем систему уравнений

$a_{i}+\sum_{i\neq j}a_{j}r_{ij}=\sum_{k}\omega_{k}r_{ki}$

Вычислим вектор коэффициентов аппроксимации $a=R_{0}^{-1}(R_{01}\omega)$ , где $R_{0}^{-1}$ – обращенная матрица корреляции ядра, а $R_{01}$ – прямоугольная матрица корреляций между ядром и хвостом с элементами $\{r_{ik}\}$ .

Итак, если ошибка приближения $\varepsilon$ достаточно мала, то

$y\approx\sum_{i}W_{i}x_{i}+\sum_{i}a_{i}\frac{x_{i}-\overline{x}_{i}}{\sigma_{i}}+\sum_{k}W_{k}\overline{x}_{k}+b$

Чтобы перейти к цивилизованной векторной записи, обозначим как $x_{0},\overline{x}_{0},w_{0}$ векторы значений, матожиданий и весов ядра, $\overline{x}_{1}$ – вектор матожиданий хвоста. Затем вычислим вектор поправки

$c=\{\frac{a_{i}}{\sigma{i}}\}$

Тогда y легко записать через скалярные произведения

$y= (w_{0}+c,x_{0})+(w_{1},\overline{x}_{1})-(c,\overline{x}_{0})+b$

Или $y=(w_{0}^{'},x_{0})+b^{'}$ , где $w_{0}^{'}=w_{0}+c$ , и $b^{'}=(w_{1},\overline{x}_{1})-(c,\overline{x}_{0})+b$ .

Выбор каналов ядра и хвоста

Итак, зная матожидание, стандартные отклонения и коэффициенты корреляции входных каналов, можно вместо вычисления хвоста в каждом пикселе слоя заранее аппроксимировать хвост с помощью ядра. Достаточно лишь вычислить вектор поправки для модификации весов и смещения, и забыть о лишних каналах как о дурном сне.

К сожалению, «забыть» получится только в одном выходном канале. Разные выходы пиксела по-разному комбинируют одни и те же входы, поэтому входной канал в одном наборе выходов будет считаться хвостом, а в другом – ядром. Поэтому разделять каналы на ядро и хвост придется индивидуально для каждого выхода.

Очевидно, выбирать хвост нужно так, чтобы дисперсия ошибки аппроксимации была минимальной. Фактически, при вычислении вектора из уравнения $R_{0}a=R_{01}\omega$ ,

$D\varepsilon=(\omega,R_{1}\omega)+(a,R_{0}a)-2(a,R_{01}\omega)=(\omega,R_{1}\omega)-(a,R_{0}a)$

Как и положено корреляционным матрицам, $R_{0}, R_{1}$ неотрицательно определенные, - не могут же дисперсии быть отрицательными (да и нулевыми – ну очень маловероятно).

Чтобы не связываться с обращением очередного варианта матрицы $R_{0}$ на каждом шаге поиска, можно для начала уменьшить дисперсию хвоста $D_{1}=(\omega,R_{1}\omega)$ .

Эта задача сродни поиску подматрицы с минимальной площадью, правда речь не о непрерывных подмассивах, а о подпоследовательностях с произвольным набором индексов, - тоже удовольствие не из приятных.

На практике неплохо работает следующий алгоритм:

Начинаем с поиска минимального элемента $|W_{k}\sigma_{k}|$ это будет начальный хвост.
Добавляем к хвосту еще один канал ядра с минимальным увеличением $D_{1}$ . Для экономии расчетов храним промежуточные суммы элементов, чтобы вычислять только изменения $\Delta D_{1}$ при модификации ядра и хвоста.
Далее в цикле стараемся улучшить результат, пробуя поочередно заменить каждый из каналов хвоста на свободные каналы ядра, сравнивая их потенциальные вклады в дисперсию.
Если уменьшить $D_{1}$ не получается, добавляем к хвосту еще один канал ядра с минимальным увеличением итоговой суммы.
Повторяем итерации, пока ошибка не приблизится к заданной границе (напр. определенный процент от общей дисперсии выхода).
Рассчитываем коэффициенты аппроксимации и вектор поправки.

Результат будет неидеальным, но довольно приличным. Более рационально, конечно, добавить в поиск расчет напрямую учитывающий остальные корреляции. Разложение Холецкого нам в помощь, - для экономии времени стоит использовать один вариант ядра для опробования сразу серии правых частей.

Послойный коллапс модели

Как это все может выглядеть в практическом плане:

Берем готовую натренированную модель. Скорее всего это будет одна из предобученных стандартных моделей, которую мы довели до ума на своих данных.
Выбираем первый слой для аппроксимации, предварительно пропустив пару-тройку начальных блоков (которые также не рекомендуется и тренировать при трансфертном обучении)
Строим вспомогательную модель для расчета матожиданий, сигм и матрицы корреляций, - заменяем выбранный слой и все последующие на слой подсчета статистики.
Прогоняем обучающий набор изображений через вспомогательную модель. Если используется предобработка данных, то стоит усреднить параметры по нескольким эпохам (матожидания и сигмы более чувствительны к таким вещам, чем коэффициенты корреляции).
По полученным данным строим ядра, хвосты и вектора поправки. Модифицируем веса и bias слоя, веса хвостов обнуляем.
Запрещаем дальнейшее обучение весов подвергшегося коллапсу слоя. В них уже и так заложена масса дополнительной информации, позволяющая существенно сократить фактическую размерность свертки.
Проводим дообучение низлежащих слоев для адаптации модели к последствиям коллапса.
Поочередно повторяем экзекуцию с оставшимися слоями.

Скорость расчетов

Универсальные пакеты-монстры типа TensorFlow не предназначены для рекордов быстродействия, но обеспечивают более чем достаточный уровень производительности (если ваша производственная среда лопается от тензорных ядер и гигабайт быстрой видеопамяти).

Однако в реальной жизни зачастую приходится умерять аппетиты самым драматичным образом. Что ж, об этом и статья. Если вам настолько не повезло, что доступны только скалярные операции, и никаких векторных SIMD-излишеств, то вы безусловно получите пропорциональную пользу от нативной реализации произведения тензора значений на разреженную в пределах 50-70% матрицу весов.

С векторными расширениями типа AVX2 придется немного повозиться. Обычно выгоднее размещать в векторном сумматоре вычисляемый подвектор выходных признаков пикселя (что соответствует формату тензоров NHWC). Но в нашем случае нужно произвольно комбинировать данные из разных входных каналов. Операция собирания регистра из разных мест памяти очень медленная. Намного эффективнее читать данные плотными векторами.

Поэтому лучше перейти к формату NCHW с поканальным размещением данных. Тогда сумматор (как и регистры операндов) будет содержать соседние точки одного и того же канала.

Самое выгодное, если удастся объединить выходные каналы в небольшие группы с более-менее одинаковым набором каналов ядра. Тогда разместив в регистрах все сумматоры группы, можно в разы сократить повторное чтение входных данных, - один загруженный входной вектор будет участвовать в изменении сразу всех выходов группы.

В любом случае, даже не прибегая к рассматриваемой здесь оптимизации, грамотная нативная реализация стандартной модели, например, на «офисном» C# с помощью указателей, Intrinsics, и продуманной буферизации даст вам как минимум двух-трех кратное ускорение на CPU с AVX2 (точнее, FMA3) относительно сборки TensorFlow под ту же архитектуру.

Спектральное прореживание

Первое, что вы заметите, если действительно попробуете аппроксимировать по описанному алгоритму свою излюбленную модель, - что при подборе порога аппроксимации (и тем самым, процента сокращенных весов) разные слои будут вести себя по-разному. Одни могут позволить себе сокращение аж до 70%, и при этом умудрятся даже немного повысить точность модели. Другие будут «упираться до последнего». (В среднем 40-50% бонус очень даже возможен!)

Очевидно, - с помощью прореживания аппроксимацией мы получаем механизм выявления узких и избыточных мест модели. И то и другое одинаково негативно влияет на точность предсказания. Узкие места – это к архитекторам, а вот избыточность, - можно ли ее уменьшить напрямую, не затевая весь этот балаган с арифметическим приближением?

Так вот же она, - наша прелесть, - матрица корреляции каналов, «сфотографированная» между соседними слоями. Методом главных компонент легко оценить «выхлоп» предыдущего слоя на предмет действительно независимой информации.

Итак, поехали! Вычисляем матрицу ковариации $C=\mathrm{cov}(X)$ на стыке между блоками, нормировать ее до матрицы корреляции не нужно. Она симметричная и неотрицательно определенная. Делаем спектральное разложение

$C=V \Lambda V^{-1}=V \Lambda V^{T}$

Изучаем отсортированный по убыванию спектр неотрицательных собственных значений. Многочисленная мелочь в конце рейтинга, - явный признак избыточности. По сути, просто препятствующий выделению важных признаков спектральный шум. И напротив, если большинство $\lambda$ существенно, скорее всего перед нами бутылочное горлышко.

Решаем, какой долей общей дисперсии (т.е. суммы собственных значений) хотим пожертвовать (процента 3 для начала будет в самый раз). Отбраковываем $\lambda$ в конце списка. Отбрасываем соответствующие им столбцы (собственные вектора) в матрице и получаем прямоугольную матрицу прореживания .

Тогда можно вставить до или после свертки слой $y=DD^{T}x$ и посмотреть на результат, предварительно адаптировав последующую часть модели. (Чтобы не искажались матожидания, можно добавить смещение $b=\overline{x} -DD^{T}\overline{x}$ .) Слой спектрального прореживания готов.

Фактически, он включает в себя понижение размерности данных. Чтобы этим воспользоваться и для улучшения производительности, можно попробовать уменьшить размерность стыка между блоками, раздельно перемножив $D^{T}$ и на матрицы весов предыдущего и следующего сверточных слоев.

К сожалению, это не всегда возможно. Если предыдущий блок заканчивается функцией активации или слоем суммирования, можно только модифицировать веса в начальной свертке следующего блока $W^{'}=WDD^{T}$ (Только не стоит забывать, что веса в TensorFlow и других пакетах обычно хранятся транспонированными).

Небольшие дополнительные хлопоты потребуются, если предыдущий блок заканчивается на BatchNorm. В этом случае от него надо просто избавиться, модифицировав bias предыдущей свертки, и умножив столбцы ее матрицы весов на соответствующие масштабирующие множители.

Не стоит ждать от спектрального прореживания крупного ускорения расчетов, а вот на предмет точности стоит и поэкспериментировать. Обычно Dropout и BatсhNorm плохо уживаются друг с другом, - случайное отключение входов при классическом прореживании это гарантированные скачки стандартного отклонения и матожидания на выходе свертки. Их последующая нормировка по пакетам только добавит хаоса.

При спектральном коллапсе у нас этой проблемы уже не будет, т.к. прореживание стационарно и разнесено с обучением во времени.

Имитация

Хватит полумер, пришло время эпической прорывной медитации на дао избыточности.

Смотрим на последний слой блока, отвечающий за уменьшение каналов в 2-6 раз. Смотрим на спектр матрицы корреляции или ковариации. Смотрим, сколько мусора можно вычистить из матриц весов с помощью аппроксимации, - как на входе блока, так и на выходе. Смотрим и думаем.

А вот бы уменьшить не индивидуальные веса внутри слоя, но масштаб расширения числа каналов в середине блока? Это бы гарантированно убавило число весов и объем расчетов, без всяких архитектурных ухищрений с разреженными матрицами.

Ой, это же топорное вмешательство в отличную структуру модели, оптимизированную, между прочим, на огромных датасетах. Уменьшить размерность блока легко, но результат будет закономерно плачевным. Расплачиваться придется падением точности предсказания при последующем неизбежном обучении как нового блока, так и всех тех, что «ниже по течению».

Стоп. Почему неизбежном? А давайте локально аппроксимируем уже имеющийся обученный блок сверточных слоев другим блоком, только попроще! Имитируем функцию исходного блока с помощью нейросетевой регрессии, и затем подсунем для адаптации остальных слоев модели готовый облегченный муляж.

Сначала построим модель для имитации: оставляем предыдущие блоки как есть, затем в параллель ставим блок-прототип и блок меньшей размерности для приближения соседа, получающие на вход одинаковые данные. Затем вычисляем разность значений выходных каналов-побратимов. В идеале разница должна быть нулем. Добавляем предпочитаемую функцию потерь, - MSE, MAE или Huber, и проводим обучение на исходных данных, никак не затрагивая модель-прототип. Тренируются только веса в муляжике! Бинго!

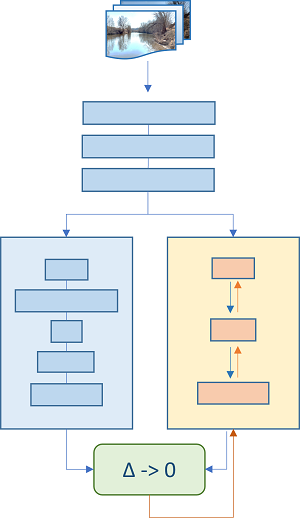
Итак, мы подменили исходный сложный блок упрощенной имитацией. Т.е. аппроксимировали его передаточную функцию другой нейросетью, - чем собственно нейросети и славятся. (Вероятно, инженеры назвали бы такой трюк суррогатным моделированием.)

У наших блоков совершенно разные задачи на момент их обучения: оригинал пыхтит над выделением признаков и получает через back propagation градиентные пинки от низлежащих «товарищей» за откровенную лажу в классификации. Имитатору на эти муки наплевать, - он только притворяется готовым результатом длительных мучений прототипа. На все готовенькое, так сказать. Пусть неидеально, пусть и с погрешностью эмулируя оригинал, но несравненно лучше такого же блока, обученного в каноническом deep learning. Который о выстраданных возможностях продвинутого прототипа – ни сном, ни духом.

Ну а дальше, понятное дело, снова каскадный коллапс, но уже не послойный, а поблочный: имитировали очередной блок, дали модели привыкнуть к изменениям, дообучив последующие слои, затем приступаем к следующему блоку. И никто не мешает сначала «подсушить» избыточный блок спектральным прореживанием или аппроксимацией, а затем уже его имитировать.

В итоге наша модель «схлапывается» не хуже нейтронной звезды, - коллапсирующие слои ужимаются, поглощают массу ценной вспомогательной информации, но расплачиваются за это необратимым отказом от дальнейшего обучения. Так что исходный прототип ни в коем случае не выбрасываем!

А вот если мы хотим не только упрощать, но и поблочно усложнять модель в "узком" месте, то "необратимого отказа от дальнейшего обучения" не потребуется. Напротив, предварительно обучив более "упитанный" блок на прототипе, и затем разрешив тренировку его весов, мы получим отличное приближение для быстрого дообучения модифицированной модели уже традиционным способом.

Вообще говоря, имитация допускает самые разные схемы обучения. Например, на каждом этапе можно сравнивать суррогат только с оригиналом, не беря в качестве прототипа следующий блок после коллапса. Это будет экивалентно пошаговому удлинению ветвей исходной модели и имитации в приведенной выше схеме. Можно переключаться между прототипом после коллапса и исходной моделью в зависимости от того, какой вариант точнее. Можно варьировать на разных этапах число обучаемых слоев в правой цепочке, и т.д., и т.п.

О чем все это было

Заходим на посадку. Пока вокруг на все лады склоняют «deep learning, deep learning», мы с вами попробовали сосредоточиться на «simple prediction», рассмотрев аппроксимацию, спектральное прореживание и имитацию. На первый взгляд это выглядит чем-то осмысленным, - разделить модель для обучения и модель для предсказания. Несомненно, у них разные задачи, но почему бы тогда и не разная архитектура? Построить вторую из первой можно описанными выше методами.

Причем архитектура может быть действительно разной, - вплоть до квантования отдельных слоев под целочисленную арифметику int8/int16. Послойный/поблочный коллапс и имитация подходят для этого как нельзя лучше. Вполне реально построить модель с целыми весами и значениями признаков, даже не покидая любимого фреймворка и уютного fp32.

(Здесь возможна следующая схема имитационного обучения: блок имитации можно составить из целочисленного слоя, полученного квантованием очередного слоя-прототипа, слоя возврата к плавающей арифметике и нескольких последующих слоев оригинала, демпфирующих ошибки квантования. На каждом шаге эта конструкция смещается вниз на один слой по прототипу.)

В любом случае, взять мощную точную модель для прототипа, и коллапсировать ее в быструю имитацию для продакшена, - довольно любопытная перспектива, не так ли. По крайней мере на задачах классификации с десятками классов и небольшим обучающим датасетом, если исходная структура модели заточена под тысячи классов и миллион картинок. Если трансфертное обучение адаптирует к вашим данным только веса модели, то здесь адаптируется и ее архитектура.

Возможно, имитационное (или, если хотите, суррогатное) обучение составит полезное дополнение к глубокому. Хотя не будем спешить с окончательными выводами. Практическая проверка большинства утверждений данной статьи пока еще слишком скромная. Но даже если эти соображения в итоге окажутся не самыми адекватными, всегда полезно взглянуть на проблему под другим углом.

Всего доброго

Ссылки

. Xiangyu Zhang, Xinyu Zhou, Mengxiao Lin, Jian Sun. ShuffleNet: An Extremely Efficient Convolutional Neural Network for Mobile Devices. https://arxiv.org/abs/1707.01083
François Chollet. Xception: Deep Learning with Depthwise Separable Convolutions. https://arxiv.org/abs/1610.02357
Andrew Howard, Mark Sandler, Grace Chu, Liang-Chieh Chen, Bo Chen, Mingxing Tan, Weijun Wang, Yukun Zhu, Ruoming Pang, Vijay Vasudevan, Quoc V. Le, Hartwig Adam. Searching for MobileNetV3. https://arxiv.org/abs/1905.02244
Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, Ruslan Salakhutdinov. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. https://jmlr.org/papers/v15/srivastava14a.html
Sergey Ioffe, Christian Szegedy. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. https://arxiv.org/abs/1502.03167

Комментарии (3)

gvozdila
17.06.2022 12:51
#24447066
+1
Отличная статья!
Не подскажете, может в каких-то библиотеках применяются некоторые из описанных методов для "сжатия" готовой сети?

Имеет ли смысл смотреть дисперсию собственных чисел для слоёв RNN, как некую "метрику" их качества?
1. neuro_diletant Автор
  17.06.2022 13:31
  #24447246
  Спасибо. Боюсь соврать, но не встречал таких готовых оптимизаций. Может из-за недостатка кругозора.
  
  Тем более не возьмусь судить о RNN, - на практике не сталкивался, особо не вникал.
  
  С одной стороны статистика она и в Африке статистика: если есть набор случайных переменных и данные о взаимной корреляции, то можно оценить и размерность скрытых независимых переменных. С другой, - если по факту распределение зависит и от внутреннего состояния, то какие тут стационарные корреляции.
1. neuro_diletant Автор
  19.06.2022 11:50
  #24452334
  Ближе всего - наборы оптимизаций TFLite