Недавно столкнулся с интересной задачей в интернете. Компания BIA Technologies организовала конкурс для математиков, в рамках которого предлагалось решить реальную прикладную задачу, а именно — построить оптимальное расписание производственных заданий для предприятия на горизонт планирования в 30 дней. Я решил поучаствовать в конкурсе, так как данный вызов показался мне интересным, плюс у меня уже был за плечами опыт реализации подобных задач на практике. В этой статье я хотел поделиться с вами результатами и продемонстрировать лучшие, на мой взгляд, подходы к решению таких задач.

Одной из первых публикаций по тематике оптимального распределения ресурсов и планирования производственных операций с использованием математических методов является работа Л.В. Канторовича - «Математические методы организации и планирования производства». Работа вышла в издательстве Ленинградского Государственного Университета в 1939 г. тиражом 1000 экземпляров и представляет расширенную стенограмму доклада, сделанного Л. В. Канторовичем в мае 1939 г. Эта работа содержит изложение нового математического аппарата, впоследствии получившего название «линейного программирования». 

Канторович в своей работе призывал к активному внедрению новейшей техники и научной организации производства, а именно применению научных концепций в составлении оптимальных планов. Вот одна из цитат:

«Существуют два пути повышения эффективности работы цеха, предприятия и целой отрасли промышленности. Один путь — это различные улучшения в технике, т. е. новые приспособления в отдельном станке, изменение технологического процесса, нахождение новых, лучших видов сырья. Другой путь, пока гораздо меньше используемый, — это улучшение в организации производства и планировании.»

В то время (в далеком 1939 году) Л.В. Канторович прозорливо предполагал, что математические методы будут активно использоваться для решения таких задач как: вопросы наилучшего распределения работы станков и механизмов, максимального уменьшения отходов, наилучшего использования сырья и местных материалов, топлива, транспорта и пр. За свои работы и инновационные подходы Л.В. Канторович удостоился множества премий и наград. В 1975 году он стал лауреатом премии по экономике памяти Альфреда Нобеля «за вклад в теорию оптимального распределения ресурсов».

Я упомянул одну из его первых работ не случайно, так как содержащиеся в ней примеры по своей сути очень похожи на конкурсное задание, которое мне предстояло решить.

«Чтобы прояснить характер задач, которые мы будем иметь в виду, приведу один очень простой пример, не требующий никаких специальных методов для решения, так как оно ясно само собой»

Л.В. Канторович мог решить данный пример в уме, о чем и заявляет в своей статье, но мы не нобелевские лауреаты, поэтому я подготовил программу, которая решит её за нас. Для решения данного примера, а также конкурсной задачи я использовал Google OR-Tools. OR-Tools – это бесплатный набор инструментов с открытым исходным кодом, который предназначен для решения задач линейного программирования, смешанно-целочисленного программирования и программирования в ограничениях. Далее предлагаю перейти уже непосредственно к постановке задачи, формулировку я сохранил авторскую.

Пример 1. Фрезерная работа при обработке деталей металлических изделий может осуществляться на разных станках — фрезерных, револьверных — более усовершенствованных, и револьверном автомате. Для определенности я рассмотрю такой вопрос. Имеется три фрезерных станка, три револьверных и один автомат. Изделие — я рассмотрю очень простой случай — состоит из двух деталей.

Выработка по каждой детали такая. За рабочий день на фрезерном станке можно изготовить 10 первых деталей либо 20 вторых; на револьверном — 20 первых либо 30 вторых; на автомате — 30 первых либо 80 вторых. При этом, если мы учтем все количество станков (фрезерных и револьверных по три, а автомат один), то за рабочий день по желанию мы можем изготовить первых деталей на каждой группе станков 30 + 60 + 30, на всех станках 120, вторых деталей 60 + 90 + 80 (табл. 1).

Необходимо составить оптимальный план производства на один рабочий день, а именно — распределить операции по оборудованию таким образом, чтобы максимизировать выпуск комплектных изделий. Напомню, что каждое готовое изделие состоит из двух деталей. В данном случае не учитываются:

• Переналадка оборудования. Требуется для того, чтобы на одном оборудовании появилась возможность изготавливать новый вид продукции. Данная операция также затрачивает временные ресурсы.

• Время на перемещение деталей.

• Перерывы в работе оборудования.

• Наличие сырья и сопутствующие расходные материалы для изготовления продукции.

• Операции по сборке готовых изделий.

Стоит отметить, что все расчеты предполагалось вести вручную, а именно обучать инженеров на местах, и учет таких детальных нюансов неизбежно превратил бы весь процесс планирования в тяжелейшую рутину. В 1939 году человечество не могло и мечтать о тех возможностях, которыми мы обладаем сейчас.

Автор предлагает выполнить два расчета. Первый вариант — это производить одинаковое количество деталей для каждой группы станков, если не стараться решить задачу на максимум, а добиваться только комплектности. Во втором случае решается задача на максимизацию выпуска комплектных деталей. Работа распределяется на то оборудование, которое максимально эффективно может производить определенный вид деталей. При этом разбивку необходимо произвести таким образом, чтобы получилось одинаковое число первых и вторых деталей.

Математическая формулировка:

Индексы:

e - идентификатор оборудования

p - индекс детали

Параметры:

Переменные:

Целевая функция:

Ограничения:

1) Задаем границы изменения значений переменных.

2) Сумма времени, затраченного на производство деталей для каждого станка, не должна превышать времени, доступного в одном рабочем дне.

3) Обеспечение комплектности финального продукта. Сумма производства деталей каждого типа равны.

import collections
from   ortools.linear_solver import pywraplp
import pandas as pd
import math
model = pywraplp.Solver.CreateSolver('CLP')
#      Данные для расчета
data = [['frez_1','frez','prod_1',10], ['frez_1','frez','prod_2',20],
       ['frez_2','frez','prod_1',10], ['frez_2','frez','prod_2',20],
       ['frez_3','frez','prod_1',10], ['frez_3','frez','prod_2',20],
       ['rev_1','rev','prod_1',20], ['rev_1','rev','prod_2',30],
       ['rev_2','rev','prod_1',20], ['rev_2','rev','prod_2',30],
       ['rev_3','rev','prod_1',20], ['rev_3','rev','prod_2',30],
       ['avt_1','avt','prod_1',30], ['avt_1','avt','prod_2',80],]  
init_data = pd.DataFrame(data, columns =['EQUIP_ID', 'EQUIP_TYPE', 'PROD_ID', 'OUTPUT']).reset_index()
equip_dict = init_data.EQUIP_ID.unique()
equip_type_dict = init_data.EQUIP_TYPE.unique()
prod_dict = init_data.PROD_ID.unique()
type_equip_prod_dict = init_data.groupby(['EQUIP_TYPE','PROD_ID']).size().reset_index().rename(columns={0:'COUNT'})
#      Переменные
vars_list = collections.defaultdict(list)
#      Блок ограничений
equipment_cons = collections.defaultdict(list)
equality_cons = []
first_case_cons = collections.defaultdict(list)
#      Целевая функция
objective = []
#      Суммарный объем  производства
equipment_type_production = collections.defaultdict(list)
total_production = collections.defaultdict(list)

for index, row in init_data.iterrows():
       time_var = model.NumVar(lb=0, ub=1, name=f"fraction_day_{row['EQUIP_ID']}_{row['PROD_ID']}")
       vars_list[row['EQUIP_ID'],row['PROD_ID']].append(time_var)
       equipment_cons[row['EQUIP_ID']].append(time_var)
       objective.append(time_var*row['OUTPUT'])
       if row['PROD_ID'] == 'prod_1':
              equality_cons.append(time_var*row['OUTPUT'])
              first_case_cons[row['EQUIP_TYPE']].append(time_var*row['OUTPUT'])
       else:
              equality_cons.append(-1*time_var*row['OUTPUT'])
              first_case_cons[row['EQUIP_TYPE']].append(-1*time_var*row['OUTPUT'])      

#      Блок ограничений
#2) Сумма времени, затраченного на производство деталей для каждого станка, не должна превышать времени, доступного в одном рабочем дне.
for equip_id in equip_dict:
       model.Add(sum(equipment_cons[equip_id]) <= 1)
#3) Обеспечение комплектности финального продукта. Сумма производства деталей каждого типа равны.
model.Add(sum(equality_cons) == 0)
#4) Ограничение для "равного выпуска" продукции. Сумма производства каждого типа деталей для каждого типа оборудования равны.
# for equip_type in equip_type_dict:
#        model.Add(sum(first_case_cons[equip_type]) == 0)
#      Целевая функция
model.Maximize(sum(objective))
#      Запуск расчета
model.EnableOutput()
model.Solve()
#      Выгрузка результатов
for index, row in init_data.iterrows():
       time = round(vars_list[row['EQUIP_ID'],row['PROD_ID']][0].solution_value(),2)
       total_production[row['PROD_ID']].append(math.floor(time*row['OUTPUT']))
       equipment_type_production[row['EQUIP_TYPE'],row['PROD_ID']].append(math.floor(time*row['OUTPUT']))
for index, row in type_equip_prod_dict.iterrows():
       print('Тип оборудования',row['EQUIP_TYPE'],'Деталь',row['PROD_ID'],'Выработка',sum(equipment_type_production[row['EQUIP_TYPE'],row['PROD_ID']]))
for prod_id in prod_dict:
       print('Деталь',prod_id,'Суммарный объем выпуска',sum(total_production[prod_id]))

Даже для такого маленького примера обнаруживается потенциал для оптимизации: за счет изменения стратегии составления плана производства удалось получить увеличение выработки на 11%.

На практике приходится иметь дело с более сложными случаями, когда необходимо найти оптимальное распределение операций на десятках видах различного оборудования. Иногда требуется составлять поминутные планы операций, учитывать рабочие смены, праздники, выходные, весь комплекс логистических ограничений. Просто угадать или подобрать по здравому смыслу оптимальное решение вряд ли получится. То есть приходится анализировать и перебирать миллионы или даже миллиарды вариантов потенциальных возможностей.

Данный пример легко решается с помощью конвенциональных методов линейного программирования, однако конкурсный пример уже не так прост. В постановке задачи имеется 78 единиц оборудования, на 67-ми из которых возможно производить только один продукт в выбранный момент времени. Всего на предприятие поступило 543 заказа, которые включают в себя 1058 вложенных подзаказов. Каждый подзаказ, в свою очередь, состоит из комплекта промежуточных продуктов. В общем за месяц необходимо произвести 11630 операций с привязкой к необходимому типу оборудования. Промежуточные продукты могут быть выполнены на нескольких типах оборудования с различным временем обработки. Необходимо распределить операции таким образом, чтобы максимизировать прибыль предприятия на горизонте планирования в 30 дней, при этом длительность операций выражена в минутах.

Задачи составления оптимального расписания широко исследованы в литературе, в связи с тем, что относительно простая математическая формулировка приводит к примерам, которые достаточно сложно решить до оптимальности. Одним из самых часто используемых критериев для оптимизации является минимизация периода изготовления продукции или минимизация временного интервала между началом первой операции и завершением последней. Имеем набор заданий и набор доступного оборудования. Каждое задание представляет из себя последовательность операций, которые необходимо назначить на оборудование, при этом операции, назначенные на каждое оборудование, не должны пересекаться между собой во времени при соблюдении строго порядка выполнения. Для решения данной задачи было принято решение использовать не традиционные методы математического моделирования, а программирование в ограничениях, из-за её комбинаторной структуры. Программирование в ограничениях является декларативной парадигмой, позволяющей выразить многие сложнейшие прикладные задачи с помощью ограничений, т.е. позволяет задать логические взаимозависимости между переменными, а также стратегию поиска. Данная парадигма широко используется для решения задач планирования производственных операций, а также для некоторых задач комбинаторной оптимизации, которые нельзя легко линеаризовать и решить с помощью традиционных методов математического программирования.

Постановка конкурсной задачи

Есть предприятие, на котором производится продукция различного ассортимента. На производство поступают заказы от клиентов на изготовление определенного типа и объема продукции. Предполагается, что портфель заказов и их стоимость известны перед началом планирования. Каждый заказ имеет свою технологическую карту производства, т.е. последовательность операций от сырья до получения готовой продукции. Операции по обработке материала выполняются на оборудовании, которое предназначено для выполнения определенного типа операций (может быть указано несколько типов операций для одного оборудования). Промежуточный продукт производственной цепи называется полуфабрикатом. Прежде чем приступить к следующей операции на оборудовании, необходимо произвести операцию переналадки оборудования (переключения оборудования на другую операцию, подготовка к обработке нового полуфабриката, очистка оборудования и т.д.). Кроме того, необходимо учитывать время перемещения полуфабрикатов продукции между цехами.

Для наглядности на Рисунке 1 приведен пример сборки простого заказа order_1. Для его изготовления необходимо собрать на линиях производства (line_1, line_2, line_3) все предварительные заготовки-полуфабрикаты на оборудовании. На одной линии находится оборудование, которое выполняет схожие операции. Как видно из рисунка, для изготовления order_1 необходимо предварительно реализовать сборку suborder_3. Прежде чем приступить к производству suborder_3, необходимо изготовить suborder_2 и переместить его от оборудования equipment_5 или equipment_6 до equipment_4. Аналогично, для производства suborder_2 необходимо произвести suborder_1 и переместить его на equipment_5 или equipment_6. Как было сказано выше — таких заказов всего 543.

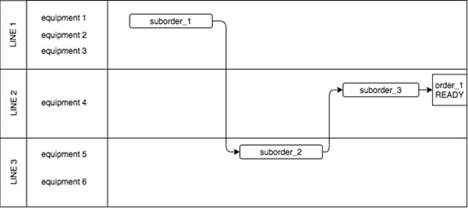
Рис. 1. Пример последовательности выполнения заказа.

Каждую операцию на оборудовании можно выразить с помощью интервальных переменных. Интервальная переменная включает в себя следующие атрибуты: начало, завершение, длительность и интенсивность. За начало и завершение интервальной переменной отвечают целочисленные переменные, длительность выражается константой, а интенсивность в самом простейшем варианте определяет существование интервальной переменной и выражается через бинарную переменную.

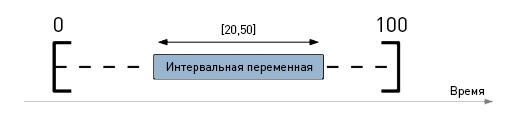
Возвращаясь к примеру, проиллюстрированному на рисунке 1, можно сказать, что в математической модели существуют интервальные переменные для всех возможных комбинаций «оборудование -> подзаказ». Например, подзаказ suborder_1 может быть выполнен на оборудовании equipment 1, equipment 2, equipment 3, то есть для подзаказа suborder_1 необходимо создать три интервальных переменных, при этом выполнить мы можем только одну из них. То есть сумма бинарных переменных, отвечающих за их существование должны быть меньше либо равны единице. Точно в такой же логике мы создаем две переменные для подзаказа suborder_2. Но теперь возникает следующая проблема: необходимо создать связку данных переменных, а именно задать очередность их выполнения. Для выполнения данного ограничения достаточно сказать, что начало выполнения переменной для подзаказа suborder_2 должно быть больше или равно, чем завершение выполнения переменной для подзаказа suborder_1 при условии их существования. Вот так просто кирпичик за кирпичиком мы выстраиваем логику составления оптимального расписания.

Ограничения

1. Если режим работы оборудования соответствует mode_0, то одновременно на этом оборудовании может выполняться только одна операция;

2. Перед каждой операцией по обработке полуфабрикатов необходимо произвести переналадку;

3. Операции переналадки и обработки полуфабриката не могут происходить одновременно;

4. Заказ может состоять из нескольких конечных продуктов. Частичное выполнение заказа к отчетной дате добавляет 0 ед. к выручке;

5. Каждый конечный продукт в заказе имеет последовательность технологических операций, которую нельзя нарушать;

6. Перемещение, переналадка и обработка полуфабриката не могут выполняться одновременно для одного полуфабриката.

Допущения

1. При планировании не учитываются потери сырья в процессе производства. Таким образом, масса готовой продукции равна массе исходного сырья.

2. Оборудование работает без перерывов. Таким образом, технологические перерывы и регламентные процедуры не учитываются при планировании.

3. Не все заказы должны быть запланированы.

Для того, чтобы подступиться к решению данного примера, первым делом нужно подготовить и сгруппировать входные данные, чтобы упростить дальнейшую работу с созданием ограничений и выстраиванием логических взаимозависимостей.

1. Длительность каждой интервальной переменной выражаем через сумму: длительность = время на переоснастку + время изготовления, так как перед каждой операцией по обработке полуфабрикатов необходимо произвести переналадку, и операции переналадки и обработки полуфабриката не могут происходить одновременно.

2. Старт и завершение операции равны 0, если интервальная переменная не используется

self.model.Add(self.all_tasks[ORDER_ID, SUBORDER_ID,SUBPRODUCT_ID,EQUIPMENT_ID,EQUIPMENT_MODE].end == 0).OnlyEnforceIf(
                    self.all_tasks[ORDER_ID, SUBORDER_ID,SUBPRODUCT_ID,EQUIPMENT_ID,EQUIPMENT_MODE].present.Not())
self.model.Add(self.all_tasks[ORDER_ID, SUBORDER_ID,SUBPRODUCT_ID,EQUIPMENT_ID,EQUIPMENT_MODE].start == 0).OnlyEnforceIf(
                    self.all_tasks[ORDER_ID, SUBORDER_ID,SUBPRODUCT_ID,EQUIPMENT_ID,EQUIPMENT_MODE].present.Not())

3. Каждый конечный продукт в заказе имеет последовательность технологических операций, которую нельзя нарушать.

self.model.Add(sum (equip_present[FROM_ORDER_ID, FROM_SUBORDER_ID,FROM_SUBPRODUCT_ID]) ==
                sum (equip_present[TO_ORDER_ID, TO_SUBORDER_ID,TO_SUBPRODUCT_ID]))
self.model.Add(sum (task_start[TO_ORDER_ID, TO_SUBORDER_ID,TO_SUBPRODUCT_ID]) >=
                sum (task_end[FROM_ORDER_ID, FROM_SUBORDER_ID,FROM_SUBPRODUCT_ID]))

Первое ограничение из данного блока необходимо для фиксирования последовательности выполнения и выбора оптимального оборудования. Второе ограничение говорит о том, что время старта последующей операции должно быть больше или равно времени завершения предыдущей операции.

4. Добавляем стандартное NoOverlap ограничение для оборудования, если режим работы оборудования соответствует mode_0, то одновременно на этом оборудовании может выполнятся только одна операция.

for machine in self.all_machines:
            self.model.AddNoOverlap(machine_to_intervals[machine])

5. Для того, чтобы учесть время на перемещение между цехами, необходимо заранее подготовить группы подзаказов, для которых существуют дополнительные ограничения на длительность перемещения. Если связанные в последовательность операции выполняются и принадлежат данной группе, то время начала последующей операции должно быть больше или равно, чем     время завершения предыдущей операции плюс время на перемещения между цехами.

decision.append(task_present_move[FROM_ORDER_ID, FROM_SUBORDER_ID,FROM_SUBPRODUCT_ID,FROM_EQUIPMENT_ID][0])
decision.append(task_present_move[TO_ORDER_ID, TO_SUBORDER_ID,TO_SUBPRODUCT_ID,TO_EQUIPMENT_ID][0])
self.model.Add(task_start_move[TO_ORDER_ID, TO_SUBORDER_ID,TO_SUBPRODUCT_ID,TO_EQUIPMENT_ID] >=
                task_end_move[FROM_ORDER_ID, FROM_SUBORDER_ID,FROM_SUBPRODUCT_ID,FROM_EQUIPMENT_ID] + [MOVE_TIME]).OnlyEnforceIf(
                    decision)

Далее на диаграмме Гантта представлен оптимальный расчет:

Код решения: https://github.com/AntonNester/Job_Shop_Competition_Case/

Составление оптимальных, практически применимых расписаний является нетривиальной задачей, которая требует согласования множества параметров и процессов. Все они образуют сложную структуру взаимосвязей, которую необходимо отражать в математических моделях. Как правило, на практике разрабатывается целый комплекс математических моделей для каждого из таких процессов. Например, в конкурсной задаче мы рассчитали только назначение задач на оборудование, однако такое расписание может оказаться не выполнимым на практике по многим причинам: из-за нехватки комплектующих, недостатка в рабочей силе, финансовых проблем и т.д. Таким образом, результаты расчета текущей математической модели будут во многом предопределены результатами предыдущих, и/или параллельных с ней математических моделей.

Как вы уже могли заметить, для решения нетривиальных и объемных задач сегодня требуется более сложный подход и грамотно подобранный инструментарий. Во времена Канторовича даже самый умный математик, имея в руках только ручку и бумагу, вряд ли смог бы найти оптимальное решение для подобной задачи. Но благодаря современным инструментам и солверам, которые есть сейчас (многие из которых есть в свободном доступе бесплатно), даже самые сложные задачи легко поддаются решению. Главное, что требуется - найти для себя понятный подход к ее решению, а это - уже чистое творчество. Самое главное - не бояться экспериментировать.