Long story short
Создают ли повороты ложные зависимости в датасете?

Небольшое исследование свойств rotate.
Представим себе, в существенно упрощенном виде, процесс скоринга.
Некто присылает информацию о себе, некую матрицу себя, банк запускает сеть и в первую очередь хочет понять, настоящая ли это матрица или обработана консультантами или просто подделана жуликами.
После этой сети банк уже понимает, что информация скорее всего неподдельная и её можно обрабатывать и применяет другие аргументы и иные сети и соглашается или отказывает заявителю.
Если банк использует только предсказание сети, то он прогорит, но об этом другая статья.
И представим для простоты, что человеческое тело это шар соискатель предоставляет просто матрицу W_SIZE x W_SIZE, ну или 128х128, например.
Почему бы и нет!
И мы не станем пытаться объять необъятное и искать все те способы обработки, что могли быть применены.
Мы возьмем матрицу w_size х w_size, заполненную случайно, мы же не знаем, что там, в реальности, и нам годятся все матрицы такого размера, и проверим, не поворачивал ли некто эту картинку(матрицу).
Т.е. будем решать максимально упрощенную задачу - в последовательности матриц/картинок будем искать те, что искусственно были повернуты. Ну и на такой же последовательности матриц будем и учить.
Использовать будем простую сеть на keras и обычные пакеты обработки, в которых есть функция "поворот"
Обычным способом грузим
import numpy as np
import cv2
from scipy import ndimage, misc, stats
from skimage import exposure
from matplotlib import pyplot as plt, colors
# work in interactive moode
%matplotlib inline
from tensorflow import keras
from tensorflow.keras import layers
from math import sqrt, sin, cos, radians
import tqdmТеперь создадим обучающую и тестовую последовательности. Создадим одну и поделим её пополам. Картинки/матрицы у нас будут такие - круг на черном фоне заполненный случайными значениями с заранее определенным распределением. При поворотах границы вносят существенные искажения, поэтому и берем круг в квадрате.
w_size = 128
w2_size = w_size // 2
R = w2_size//2
center = (w2_size, w2_size)
scale = 1
circle = np.zeros((w_size, w_size), dtype='uint8')
for i in range(w_size):
for j in range(w_size):
ii = float(i - w2_size)
jj = float(j - w2_size)
r = sqrt(ii*ii + jj*jj)
if r < R:
circle[i,j] = 1
def shift(x,y,w2_size):
ii = float(x - w2_size)
jj = float(y - w2_size)
return ii,jj
def rotate(ii,jj,teta):
i1 = ii*cos(teta) + jj*sin(teta)
j1 = ii*sin(teta) + jj*cos(teta)
return i1,j1
circle = np.zeros((w_size, w_size), dtype='int')
for i in range(w_size):
for j in range(w_size):
ii,jj = shift(i,j,w2_size)
r = sqrt(ii*ii + jj*jj)
if r < R:
circle[i,j] = 1
fig, ax = plt.subplots(1, 1,figsize=(5, 5))
ax.set_axis_off()
ax.set_title("circle")
ax.imshow(circle.squeeze(), cmap='gray', norm=None)

Первый эксперимент
Первый эксперимент проведем умозрительно, на бумаге.
Заполним квадрат с помощью numpy.random.uniform, после повернем с помощью ndimage.rotate на случайно выбранный угол.
Или не повернем. И из таких квадратов составим наши последовательности.
И признак для классификации оставим такой - 0, если не повернут и 1 если квадрат повернут.
И в каждом квадрате вырезаем центральный круг. Т.е. артефакты, вызванные граничными точками, убираем.
Нам нужен только круг в центре.
Очевидно, что сеть их отличит очень уверенно, на графиках гистограмм можем увидеть подтверждение ЦПТ, исходные картинки с ровной (почти) гистограммой, повернутые картинки дают гистограмму в виде горба ( очень похож на Гауссиан )
Так что дальше будем проводить эксперименты только с numpy.random.normal распределением.
Для тех, кто не верит на слово, пожалуйста, код.
num_classes = 2
train_len = 5000
test_len = 1000
input_shape = (w_size, w_size, 1)
X = np.zeros((train_len+test_len, w_size, w_size, 1), dtype='float32')
Y = np.zeros(train_len+test_len, dtype='float32')
mu = 0.25
sigma = 0.05
for iii in tqdm.tqdm(range(train_len + test_len)):
angle = np.random.randint(-5,5)+ 45
n = np.random.uniform(0.25, 0.75, size=(w_size, w_size))
t = np.zeros((w_size, w_size), dtype='float')
t[circle>0] = n[circle>0]
r = ndimage.rotate(n, angle, reshape=False, mode='nearest')
tt = np.zeros((w_size, w_size), dtype='float')
tt[circle>0] = r[circle>0]
choise = np.random.randint(0, high=65535, dtype=int) % 2
if choise == 1:
X[iii,:,:,0] = t[:,:]
Y[iii] = 0
else:
X[iii,:,:,0] = tt[:,:]
Y[iii] =1
yy_train = np.array(keras.utils.to_categorical(Y[:train_len], num_classes))
yy_test = np.array(keras.utils.to_categorical(Y[train_len:], num_classes))
xx_train = np.array(X[:train_len])
xx_test = np.array(X[train_len:])
print(xx_train.shape, yy_train.shape)
print(xx_test.shape, yy_test.shape)
nrows=2
ncols=4
fig, ax = plt.subplots(nrows*2, ncols,figsize=(16, 20))
for ii in range(nrows):
for jj in range(ncols):
random_characters = int(np.random.uniform(0,train_len))
ax[2*ii,jj].set_axis_off()
ax[2*ii,jj].set_title(str(int(Y[random_characters])))
ax[2*ii,jj].imshow(X[random_characters].squeeze(), cmap='gray', norm=None)
tx = X[random_characters]
ax[2*ii+1,jj].hist(255.*X[random_characters].flatten(), np.arange(1,256), facecolor='blue',histtype='step')
plt.show(block=True)
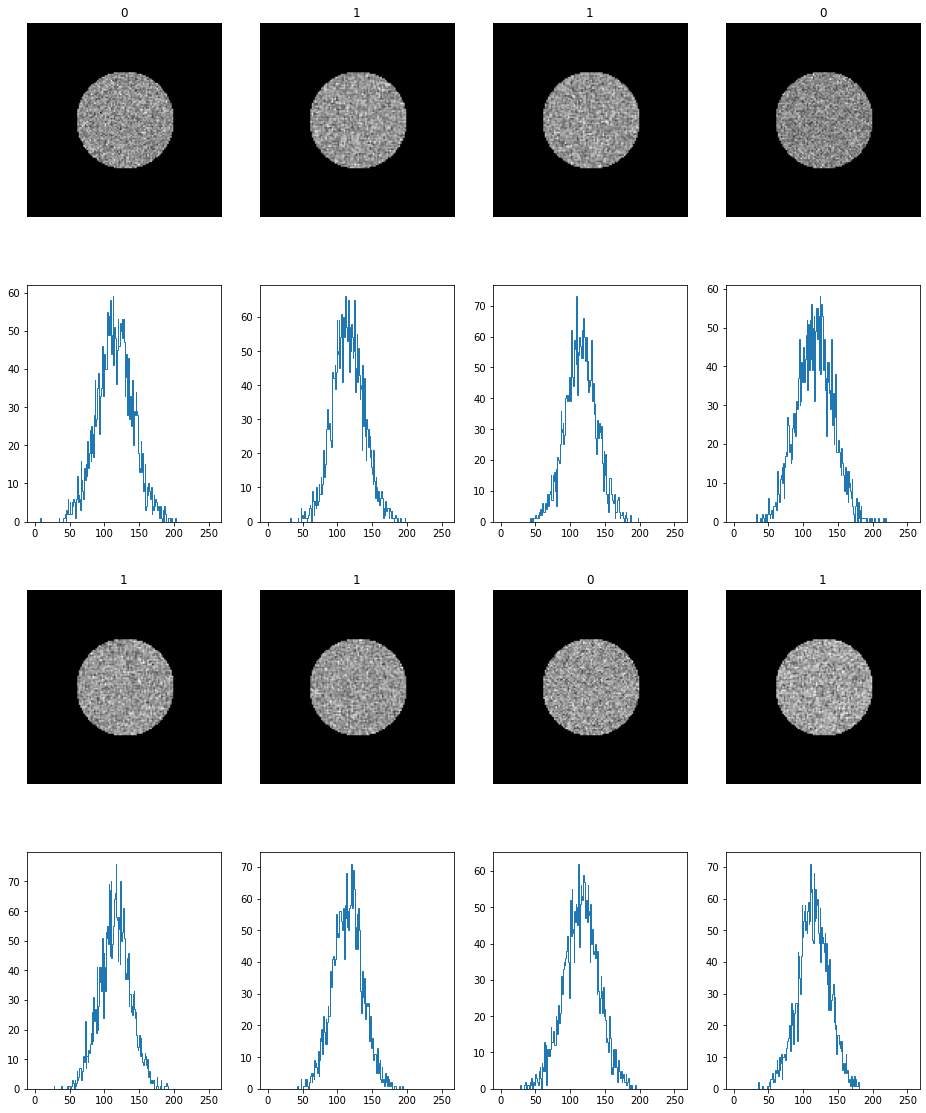
Второй эксперимент
Второй эксперимент проведем, заполняя исходные квадраты случайными значениями уже с numpy.random.normal распределением.
Точно так же построим последовательность картинок, заполненных случайными значениями нормального распределения. И часть картинок повернем.
Оказывается сеть спокойно их различает.
Простой анализ гистограмм показывает, что они разные у повернутых и оригинальных картинок. Очень похожи, но совсем разные. Тест на нормальность почти все повернутые не проходят.
X = np.zeros((train_len+test_len, w_size, w_size, 1), dtype='float32')
Y = np.zeros(train_len+test_len, dtype='float32')
mu = 0.45
sigma = 0.1
for iii in tqdm.tqdm(range(train_len + test_len)):
angle = np.random.randint(-5,5)+ 45
n = np.random.normal(mu, sigma, size=(w_size, w_size))
t = np.zeros((w_size, w_size), dtype='float')
t[circle>0] = n[circle>0]
r = ndimage.rotate(n, angle, reshape=False, mode='nearest')
tt = np.zeros((w_size, w_size), dtype='float')
tt[circle>0] = r[circle>0]
choise = np.random.randint(0, high=65535, dtype=int) % 2
if choise == 1:
X[iii,:,:,0] = t[:,:]
Y[iii] = 0
else:
X[iii,:,:,0] = tt[:,:]
Y[iii] =1
yy_train = np.array(keras.utils.to_categorical(Y[:train_len], num_classes))
yy_test = np.array(keras.utils.to_categorical(Y[train_len:], num_classes))
xx_train = np.array(X[:train_len])
xx_test = np.array(X[train_len:])
print(xx_train.shape, yy_train.shape)
print(xx_test.shape, yy_test.shape)
nrows=2
ncols=4
fig, ax = plt.subplots(nrows*2, ncols,figsize=(16, 20))
for ii in range(nrows):
for jj in range(ncols):
random_characters = int(np.random.uniform(0,train_len))
ax[2*ii,jj].set_axis_off()
ax[2*ii,jj].set_title(str(int(Y[random_characters])))
ax[2*ii,jj].imshow(X[random_characters].squeeze(), cmap='gray', norm=None)
ax[2*ii+1,jj].hist(255.*X[random_characters].flatten(), np.arange(1,256),\
facecolor='blue',histtype='step')
plt.show(block=True)
model = keras.Sequential(
[
keras.Input(shape=input_shape),
layers.Conv2D(32, kernel_size=(3, 3), activation="relu"),
layers.Conv2D(32, kernel_size=(3, 3), activation="relu"),
layers.MaxPooling2D(pool_size=(2, 2)),
layers.Conv2D(64, kernel_size=(3, 3), activation="relu"),
layers.Conv2D(64, kernel_size=(3, 3), activation="relu"),
# layers.MaxPooling2D(pool_size=(2, 2)),
layers.Flatten(),
layers.Dropout(0.5),
layers.Dense(128, activation="relu"),
layers.Dense(num_classes, activation="softmax"),
]
)
batch_size = 25
epochs = 5
num_classes = 2
n_bins = 256
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
#model.summary()
model.fit(xx_train, yy_train, batch_size=batch_size, epochs=epochs,
validation_data=(xx_test, yy_test), verbose = 2)
Epoch 1/5
200/200 - 6s - loss: 0.2437 - accuracy: 0.8638 - val_loss: 4.7537e-05 - val_accuracy: 1.0000
Epoch 2/5
200/200 - 4s - loss: 3.7514e-05 - accuracy: 1.0000 - val_loss: 2.2031e-05 - val_accuracy: 1.0000
Epoch 3/5
200/200 - 4s - loss: 1.8480e-05 - accuracy: 1.0000 - val_loss: 1.1520e-05 - val_accuracy: 1.0000
Epoch 4/5
200/200 - 4s - loss: 1.0300e-05 - accuracy: 1.0000 - val_loss: 6.6436e-06 - val_accuracy: 1.0000
Epoch 5/5
200/200 - 4s - loss: 5.9791e-06 - accuracy: 1.0000 - val_loss: 4.1065e-06 - val_accuracy: 1.0000
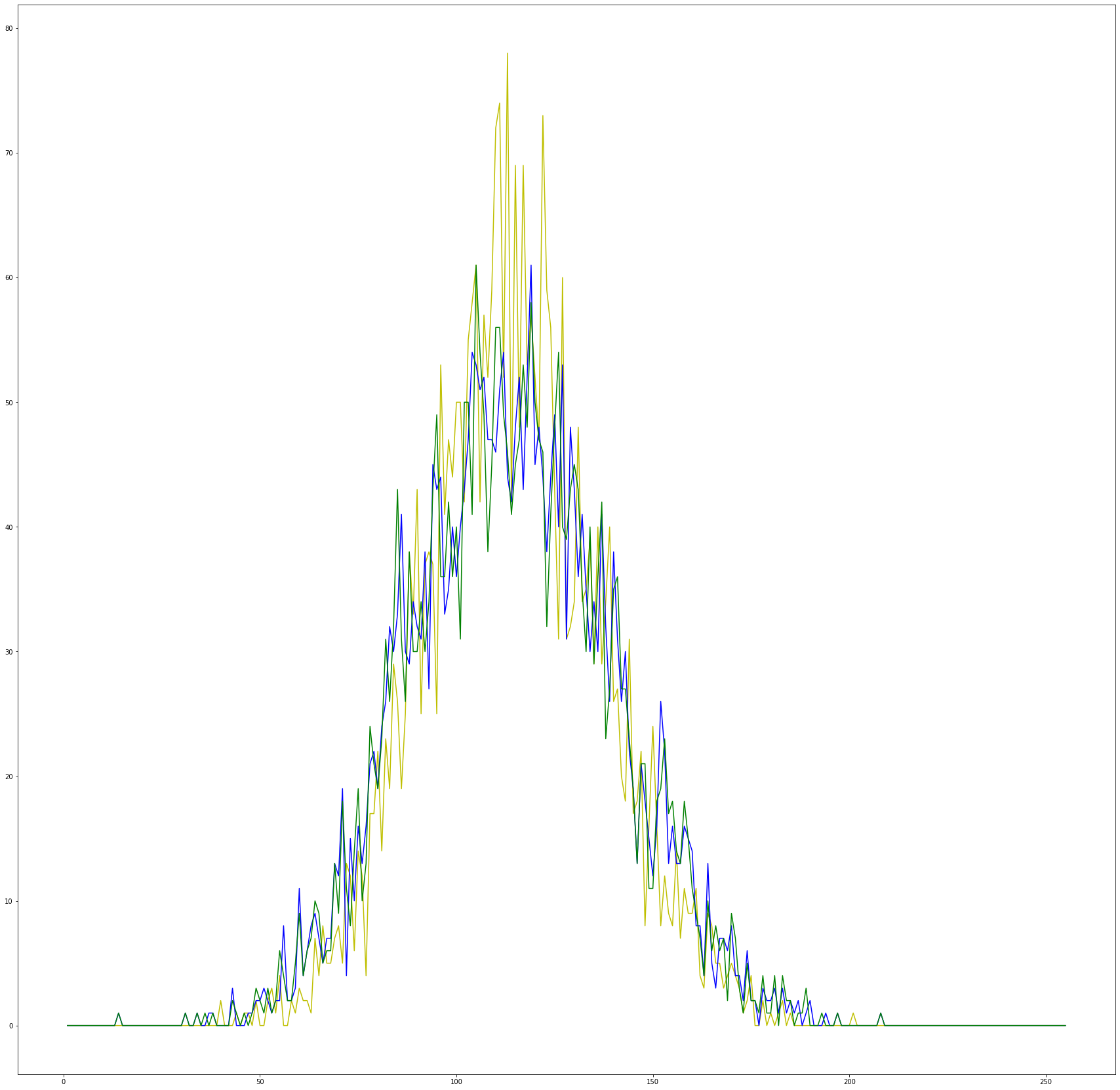
Третий эксперимент
Третий эксперимент проведем, заполняя исходные квадраты случайными значениями с numpy.random.normal распределением.
Точно так же построим последовательность картинок, заполненных случайными значениями нормального распределения.
И часть картинок повернем.
Но теперь повернутые картинки немного исказим так, что бы гистограмма повернутой совпадала с гистограммой оригинальной картинки.
И тут чудо, сеть не может отличить повернутые картинки от оригинальных, если гистограммы мало отличаются.
Не так уж он оказался умен, этот ваш искусственный интеллект
X = np.zeros((train_len+test_len, w_size, w_size, 1), dtype='float32')
Y = np.zeros(train_len+test_len, dtype='float32')
mu = 0.45
sigma = 0.1
view_test = np.random.randint(0, train_len+test_len, (3))
for iii in tqdm.tqdm(range(train_len + test_len)):
angle = np.random.randint(-5,5)+ 45
n = np.random.normal(mu, sigma, size=(w_size, w_size))
t = np.zeros((w_size, w_size), dtype='float')
t[circle>0] = n[circle>0]
tf = t.flatten()
r = ndimage.rotate(n, angle, reshape=False, mode='nearest')
tt = np.zeros((w_size, w_size), dtype='float')
tt[circle>0] = r[circle>0]
tts = tt.copy()
ttf = tt.flatten()
step = np.arange(0., 1., 1./255.)
for ii in range(1):
for i in range(1,253):
T = np.sum(np.bitwise_and(tf>step[i], tf<step[i+1]))
TT = np.sum(np.bitwise_and(ttf>step[i], ttf<step[i+1]))
T_TT = abs(T-TT)
if T_TT == 0:
continue
if T>TT:
jj = 0
while True:
tt_array = np.nonzero(np.bitwise_and(ttf>step[i+1],ttf<step[i+2]))[0]
if len(tt_array)>=T_TT or i+jj > w_size-2:
break
ttf[ttf>step[i+2]] -=step[1]
jj += 1
indices = np.arange(len(tt_array))
np.random.shuffle(indices)
for j in range(min(len(tt_array), T_TT)):
ttf[tt_array[indices[j]]] -= step[1]
else:
tt_array = np.nonzero(np.bitwise_and(ttf>step[i], ttf<step[i+1]))[0]
if len(tt_array) != 0:
indices = np.arange(len(tt_array))
np.random.shuffle(indices)
for j in range(min(len(tt_array), T_TT)):
ttf[tt_array[indices[j]]] +=step[1]
tt = ttf.reshape(w_size,w_size)
choise = np.random.randint(0, high=65535, dtype=int) % 2
if choise == 1:
X[iii,:,:,0] = t[:,:]
Y[iii] = 0
else:
tt = ttf.reshape(w_size,w_size)
X[iii,:,:,0] = tt
Y[iii] =1
if iii in view_test:
random_idx = int(np.random.uniform(0,train_len))
alpha = 0.05
fig, axs = plt.subplots(1, 3, figsize=(30, 10))
stat, p = stats.normaltest(t[circle>0].flatten())
if p > alpha:
axs[0].set_title("Оригинал Принять "+ str(p))
else:
axs[0].set_title("Оригинал Отклонить ?"+ str(p))
axs[0].set_axis_off()
axs[0].imshow(t, cmap="gray")
stat, pp = stats.normaltest(tt[circle>0].flatten())
if pp > alpha:
axs[1].set_title("выровненный поворот Принять "+ str(pp))
else:
axs[1].set_title("выровненный поворот Отклонить "+ str(pp))
axs[1].set_axis_off()
axs[1].imshow(tt, cmap="gray")
stat, p = stats.normaltest(tts[circle>0].flatten())
if p > alpha:
axs[2].set_title("просто поворот Принять "+ str(p))
else:
axs[2].set_title("просто поворот Отклонить "+ str(p))
axs[2].set_axis_off()
axs[2].imshow(tts, cmap="gray")
tt_hist,b = np.histogram(256*tt.flatten(), np.arange(1,257))
tts_hist,b = np.histogram(256*tts.flatten(), np.arange(1,257))
t_hist,_ = np.histogram(256*t.flatten(), np.arange(1,257))
fig, axs = plt.subplots(1, 1, figsize=(30, 30))
bins = np.arange(1,256)
axs.plot(bins, tts_hist, 'y')
axs.plot(bins, tt_hist, 'b')
axs.plot(bins, t_hist, 'g')
plt.show(block=True)
yy_train = np.array(keras.utils.to_categorical(Y[:train_len], num_classes))
yy_test = np.array(keras.utils.to_categorical(Y[train_len:], num_classes))
xx_train = np.array(X[:train_len])
xx_test = np.array(X[train_len:])
print(xx_train.shape, yy_train.shape)
print(xx_test.shape, yy_test.shape)

Сеть та же самая.
batch_size = 25
epochs = 5
num_classes = 2
n_bins = 256
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
#model.summary()
model.fit(xx_train, yy_train, batch_size=batch_size, epochs=epochs,
validation_data=(xx_test, yy_test), verbose = 2)
Epoch 1/5
200/200 - 4s - loss: 0.6990 - accuracy: 0.4966 - val_loss: 0.6932 - val_accuracy: 0.4970
Epoch 2/5
200/200 - 4s - loss: 0.6932 - accuracy: 0.4992 - val_loss: 0.6932 - val_accuracy: 0.4970
Epoch 3/5
200/200 - 4s - loss: 0.6932 - accuracy: 0.4988 - val_loss: 0.6931 - val_accuracy: 0.5030
Epoch 4/5
200/200 - 4s - loss: 0.6932 - accuracy: 0.4930 - val_loss: 0.6931 - val_accuracy: 0.4970
Epoch 5/5
200/200 - 4s - loss: 0.6932 - accuracy: 0.4990 - val_loss: 0.6932 - val_accuracy: 0.4970
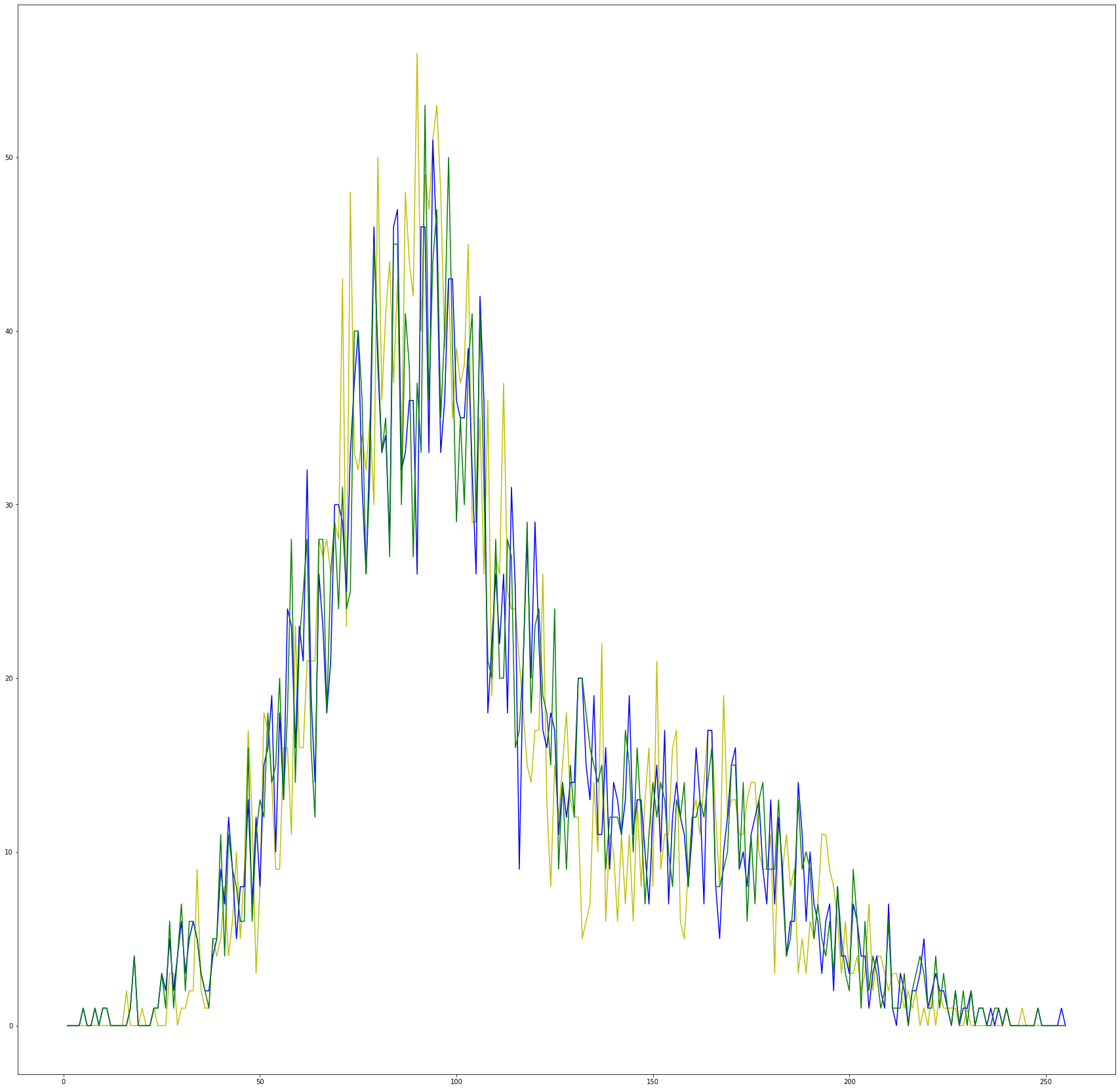
Главный эксперимент
Ну и главный эксперимент проведем на эллипсах. Очень хорошая и удобная геометрическая фигура. Картинки для испытаний создадим так - тот же квадрат, заполненный случайными данными нормального распределения и внутри квадрата эллипс, заполненный случайными значениями тоже нормального распределения, но с другими ожиданием и дисперсией. Так же после поворота выровняем гистограмму, так же как и в предыдущем эксперименте. И вот такие повороты нейронная простая сеть отлично находит.
Т.е. если картинка структурирована и неоднородна, то даже если сегменты по распределению не искажаются - все равно сеть определяет поворот исходной картинки.
w_size = 128
w2_size = w_size // 2
R = w2_size//2
center = (w2_size, w2_size)
scale = 1
RR = R //2
A = RR + 4
B = RR - 4
c = sqrt(float(A*A - B*B))
num_classes = 2
train_len = 5000
test_len = 1000
input_shape = (w_size, w_size, 1)
circle = np.zeros((w_size, w_size), dtype='uint8')
for i in range(w_size):
for j in range(w_size):
ii = float(i - w2_size)
jj = float(j - w2_size)
r = sqrt(ii*ii + jj*jj)
if r < R:
circle[i,j] = 1
def shift(x,y,w2_size):
ii = float(x - w2_size)
jj = float(y - w2_size)
return ii,jj
def rotate(ii,jj,teta):
i1 = ii*cos(teta) + jj*sin(teta)
j1 = ii*sin(teta) + jj*cos(teta)
return i1,j1
circle = np.zeros((w_size, w_size), dtype='int')
for i in range(w_size):
for j in range(w_size):
ii,jj = shift(i,j,w2_size)
r = sqrt(ii*ii + jj*jj)
if r < R:
circle[i,j] = 1
def ellipse_p(teta_grad):
ellipse = np.zeros((w_size, w_size), dtype='float32')
teta = radians(teta_grad)
ci1, cj1 = rotate( c,0,teta)
ci2, cj2 = rotate(-c,0,teta)
for i in range(w_size):
for j in range(w_size):
ii,jj = shift(i,j,w2_size)
r1 = sqrt((ii-ci1)*(ii-ci1) + (jj-cj1)*(jj-cj1))
r2 = sqrt((ii-ci2)*(ii-ci2) + (jj-cj2)*(jj-cj2))
if r1+r2 < 2*A:
ellipse[i,j] = 255
return (ellipse)
teta_grad = 45.0
ellipse = ellipse_p(teta_grad)
fig, ax = plt.subplots(1, 2,figsize=(10, 20))
ax[0].set_axis_off()
ax[0].set_title("circle")
ax[0].imshow(circle.squeeze(), cmap='gray', norm=None)
ax[1].set_axis_off()
ax[1].set_title("ellipse")
ax[1].imshow(ellipse.squeeze(), cmap='gray', norm=None)

X = np.zeros((train_len+test_len, w_size, w_size, 1), dtype='float32')
Y = np.zeros(train_len+test_len, dtype='float32')
mu = 0.35
sigma = 0.1
el_mu = 0.65
el_sigma = 0.1
view_test = np.random.randint(0, train_len+test_len, (3))
for iii in tqdm.tqdm(range(train_len + test_len)):
angle = np.random.randint(-5,5)+ 45
n = np.random.normal(mu, sigma, size=(w_size, w_size))
el = np.random.normal(el_mu, el_sigma, size=(w_size, w_size))
t = np.zeros((w_size, w_size), dtype='float')
t[circle>0] = n[circle>0]
ellipse = ellipse_p(angle)
t[ellipse>0] = el[ellipse>0]
tf = t.flatten()
ellipse = ellipse_p(0)
n[ellipse>0] = el[ellipse>0]
r = ndimage.rotate(n, angle, reshape=False, mode='nearest')
tts = np.zeros((w_size, w_size), dtype='float')
tts[circle>0] = r[circle>0]
ttf = tts.flatten()
step = np.arange(0., 1., 1./255.)
for ii in range(1):
for i in range(1,253):
T = np.sum(np.bitwise_and(tf>step[i], tf<step[i+1]))
TT = np.sum(np.bitwise_and(ttf>step[i], ttf<step[i+1]))
T_TT = T-TT
if abs(T_TT) == 0:
continue
if T>TT:
jj = 0
while True:
tt_array = np.nonzero(np.bitwise_and(ttf>step[i+1],ttf<step[i+2]))[0]
if len(tt_array)>=T_TT or i+jj > w_size-2:
break
ttf[ttf>step[i+2]] -=step[1]
jj += 1
indices = np.arange(len(tt_array))
np.random.shuffle(indices)
for j in range(min(len(tt_array), T_TT)):
ttf[tt_array[indices[j]]] -= step[1]
else:
tt_array = np.nonzero(np.bitwise_and(ttf>step[i], ttf<step[i+1]))[0]
if len(tt_array) != 0:
indices = np.arange(len(tt_array))
np.random.shuffle(indices)
for j in range(min(len(tt_array), abs(T_TT))):
ttf[tt_array[indices[j]]] +=step[1]
tt = ttf.reshape(w_size,w_size)
choise = np.random.randint(0, high=65535, dtype=int) % 2
if choise == 1:
X[iii,:,:,0] = t[:,:]
Y[iii] = 0
else:
tt = ttf.reshape(w_size,w_size)
X[iii,:,:,0] = tt
Y[iii] =1
if iii in view_test:
random_idx = int(np.random.uniform(0,train_len))
alpha = 0.05
fig, axs = plt.subplots(1, 3, figsize=(30, 10))
axs[0].set_axis_off()
axs[1].set_axis_off()
axs[2].set_axis_off()
axs[0].imshow(t, cmap="gray")
axs[1].imshow(tt, cmap="gray")
axs[2].imshow(tts, cmap="gray")
tt_hist,b = np.histogram(256*tt.flatten(), np.arange(1,257))
tts_hist,b = np.histogram(256*tts.flatten(), np.arange(1,257))
t_hist,_ = np.histogram(256*t.flatten(), np.arange(1,257))
fig, axs = plt.subplots(1, 1, figsize=(30, 30))
bins = np.arange(1,256)
axs.plot(bins, tts_hist, 'y')
axs.plot(bins, tt_hist, 'b')
axs.plot(bins, t_hist, 'g')
plt.show(block=True)
yy_train = np.array(keras.utils.to_categorical(Y[:train_len], num_classes))
yy_test = np.array(keras.utils.to_categorical(Y[train_len:], num_classes))
xx_train = np.array(X[:train_len])
xx_test = np.array(X[train_len:])
print(xx_train.shape, yy_train.shape)
print(xx_test.shape, yy_test.shape)
print(np.min(X), np.max(X))
batch_size = 25
epochs = 5
num_classes = 2
n_bins = 256
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])
#model.summary()
model.fit(xx_train, yy_train, batch_size=batch_size, epochs=epochs,
validation_data=(xx_test, yy_test), verbose = 2)
Epoch 1/5
200/200 - 4s - loss: 0.3143 - accuracy: 0.8330 - val_loss: 0.0030 - val_accuracy: 0.9990
Epoch 2/5
200/200 - 4s - loss: 0.0077 - accuracy: 0.9978 - val_loss: 2.2245e-04 - val_accuracy: 1.0000
Epoch 3/5
200/200 - 4s - loss: 0.0019 - accuracy: 0.9994 - val_loss: 4.2272e-04 - val_accuracy: 1.0000
Epoch 4/5
200/200 - 4s - loss: 0.0091 - accuracy: 0.9966 - val_loss: 9.0115e-04 - val_accuracy: 0.9990
Epoch 5/5
200/200 - 4s - loss: 0.0105 - accuracy: 0.9964 - val_loss: 0.0067 - val_accuracy: 0.9980Краткое резюме.
Если в вашем датасете с картинками не выровненные классы, и вы решили добавить картинок для выравнивания с помощью аугментации, то результат будет удивительным и коварным.

