В былые времена люди без иронии и преувеличения называли самым ценным ресурсом информацию. И чем ценнее информация, тем лучше она должна быть сокрыта от любопытных глаз и ушей. Этот тезис как никогда актуален в наши дни. Сопряжение реального и цифрового миров привело к тому, что множество данных, некогда хранящихся на физических носителях, преобразовались в цифровой вид. А чем сложнее форма, в которой пребывает информация, тем сложнее ее защитить от потенциального злоумышленника. Ввиду этого разнообразие новых методов шифрования данных не прекращает расти. И вот ученые из Дьюкского университета (США) разработали новый метод кодирования и декодирования информации, который использует искусственный интеллект и бактерии. Как бактерии помогают шифровать данные, какова задача ИИ в этом процессе, и насколько такое шифрование эффективно? Ответы на эти вопросы мы найдем в докладе ученых.

Основа исследования

Любой процесс кодирования, независимо от методики, можно описать как процесс преобразования информации из исходного формата в выходной, следуя определенным правилам. Динамические системы кодирования делают именно так, поскольку могут генерировать определенные выходные данные в соответствии с заданными входными данными.

Декодирование можно описать, как и кодирование, но в обратном порядке, когда из выходных данных мы возвращаемся к исходным. В зависимости от системы декодирование может быть очевидным, сложным или невозможным. Поскольку системы самоорганизации могут генерировать многомерные выходные данные, они особенно полезны для кодирования ценной информации.

Одним из примеров динамической системы кодирования является клеточный автомат (CA от cellular automaton), который преобразует решетку клеток из простой начальной конфигурации в самоорганизующуюся последовательность или пространственный шаблон в соответствии с набором правил.

В 1985 году Стивен Вольфрам в своем труде «Cryptography with Cellular Automata» предложил использовать хаотическое правило для генерации случайных последовательностей для кодирования информации.

В такой системе кодирование является детерминированным — каждая начальная конфигурация соответствует уникальному выходному шаблону. Однако из-за хаотичного характера декодирование входных данных из заданного выходного паттерна невозможно с вычислительной точки зрения без предварительного знания правил обновления. Таким образом, система теоретически может служить основой для цифровой криптографии.

Несмотря на то, что такое кодирование будет весьма надежным, хаотичность сильно ограничивает его применение. Как и другие динамические системы, демонстрирующие детерминированный хаос, окончательные модели, генерируемые CA, чрезвычайно чувствительны к возмущениям и лишены статистических закономерностей. Таким образом, незначительное изменение исходной конфигурации или процесса кодирования может привести к резкому изменению конечных паттернов (эффект лавины). Если же в кодировании и передаче присутствует шум, то в декодировании будут ошибки, даже если правила известны.

В отличие от хаотических систем многие природные системы конвергентны. То есть для одних и тех же или подобных входных конфигураций и условий окружающей среды окончательные шаблоны имеют глобальное сходство, несмотря на локальные различия. Это свойство иногда называют «краем хаоса», а примерами являются химические реакции и кортикальные сети.

Ученые отмечают, что многие биологические системы формирования паттернов также попадают в эту категорию. К примеру, несмотря на незначительные различия, узоры шерсти в значительной степени определяются геномами животных и позволяют идентифицировать разные виды. А у микробов один и тот же бактериальный штамм может вырасти в колонии различной формы и размера в разных условиях роста. Несмотря на эти эмпирические примеры, потенциал и ограничения кодирования и декодирования информации с использованием биологической самоорганизации остаются неисследованными.

В рассматриваемом нами сегодня труде ученые решили использовать вышеописанные системы для создания распределенного кодирования информации (1A).

Результаты исследования

Любые динамические системы, в том числе генерирующие самоорганизующиеся паттерны, могут служить основой для кодирования и декодирования информации. Однако, как отмечают ученые, для обеспечения безопасного кодирования и надежного декодирования динамика системы должна соответствовать ряду эвристических критериев.

Во-первых, выходные паттерны достаточно сложны и разнообразны, так что различные начальные конфигурации будут генерировать различимые выходные паттерны.

Во-вторых, генерация паттернов подвержена стохастичности, но остается конвергентной. То есть в повторяющихся процессах генерации паттернов одна и та же начальная конфигурация с небольшим шумом или возмущениями должна генерировать выходные паттерны, которые примерно одинаковы, но отличаются незначительными деталями.

В-третьих, в то время как различные группы паттернов, возникающих при различных начальных условиях, могут быть декодированы правильно сконструированным декодером, их различия трудно различить невооруженным глазом.

В качестве практического подтверждения вышеописанной концепции ученые решили использовать крупнозернистую модель самоорганизованного формирования паттернов. Модель была разработана для имитации качественных аспектов динамики ветвления колоний Pseudomonas aeruginosa. Каждое моделирование начиналось с предопределенной конфигурации посева клеток, который в последствии превращался в разветвляющуюся колонию.

На процесс формирования паттерна влияют два источника случайного шума. Один исходит из изменчивости начального распределения засеянных клеток, а второй — из лежащей в основе кинетики роста. При соответствующем выборе параметров (включая уровень шума) динамика формирования паттерна удовлетворяет всем перечисленным выше критериям.


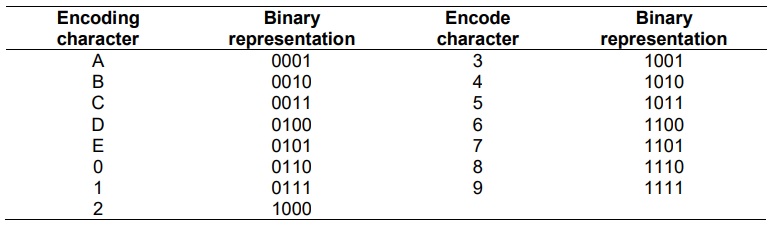
Таблица №1

Чтобы продемонстрировать кодирование, ученые использовали словарь из 15 символов (букв A–E и цифр 0–9), выраженный двоичным кодом (0001–1111; таблица выше).


Изображение №1

Каждое двоичное число соответствует конфигурации заполнения клеток в массиве, похожем на шрифт Брайля, в момент времени 0 (1B): цифра «1» соответствует точечному заполнению, указывающему на присутствие клетки, тогда как цифра «0» указывает на отсутствие клетки.

Как упоминалось выше, моделирование подвержено двум источникам шума: изменчивости при посеве и изменчивости во время роста. Первое может происходить из-за маргинального, но неизбежного неравномерного высева клеток, а второе может происходить из-за врожденной гетерогенности экспрессии клеточных генов, подвижности или небольшого внешнего возмущения.

Таким образом, повторные симуляции из одной и той же исходной конфигурации генерируют аналогичные конечные шаблоны с небольшими отличиями, которые в совокупности кодируют идентичность входной конфигурации (1C).

Симуляции были настроены таким образом, чтобы ни сопоставление между начальными конфигурациями и образцами колоний, ни разница между образцами, соответствующими разным входам, не были очевидны невооруженному глазу. Как говорят ученые, чтобы обеспечить надежное декодирование, нужен надежный метод для навигации по этой визуальной сложности.

Прямой метод — это поиск методом грубой силы, при котором моделируются все возможные шаблоны для каждой начальной конфигурации, чтобы установить эмпирическое сопоставление между входом и выходом.

Несмотря на кажущуюся простоту, этот подход требует больших вычислительных ресурсов и крайне непрактичен, поскольку паттерны обучения представляют собой 8-битные изображения размером 80 х 80 пикселей, что дает до 2^8x80x80 ~ 10¹⁵⁴¹² возможных вариантов.

В качестве альтернативы можно использовать классификацию изображений с помощью сверточных нейронных сетей (CNN от convolutional neural networks). Наблюдая за достаточным количеством примеров, CNN учится группировать изображения по их категориям.

Во время обучения CNN декодер принимает в качестве входных данных изображения паттернов (созданные в результате повторяющихся симуляций) и обновляет свои обучаемые параметры для классификации паттернов на основе исходных начальных конфигураций. При достаточном количестве повторов в каждом классе обученная нейросеть смогла с высокой точностью различать паттерны, соответствующие 15 символам (1D). Другими словами, при наличии 800 повторяющихся паттернов в обучающем наборе можно достичь 93% точности декодирования.

В процессе создания эффективной системы кодирования необходимо было повысить значения определенных параметров: емкость кодирования — способность паттернов кодировать информацию и безопасность кодирования — устойчивость системы к утечке данных неавторизованным сторонам.

Следовательно, систему можно считать производительной, если она может правильно кодировать больше символов, а ее безопасность оценивается неспособностью злоумышленника построить декодер на базе утекших данных. Например, точность отдельного декодера, построенного на базе только 10 повторов на класс, составляет менее 20% (1D), что лишь немного лучше, чем случайное угадывание (1/15).

Производительность системы может быть настроена путем модулирования параметров модели генерации паттернов. Было создано 16 смоделированных обучающих наборов данных с различными паттернами путем настройки этих двух параметров. Основываясь на их окончательном виде, результаты были разделены на три подгруппы: дискообразные (большой диск, занимающий всю область роста), тривиальные (конечный паттерн идентичен исходной конфигурации) и ветвящиеся.

Дискообразные колонии невозможно различить независимо от размера обучающих данных — таким образом, входная информация «теряется» после роста колонии клеток. И наоборот, тривиальные шаблоны допускают простейшее декодирование, что совершенно недопустимо. Следовательно, идеальным вариантом паттернов являются именно ветвящиеся.


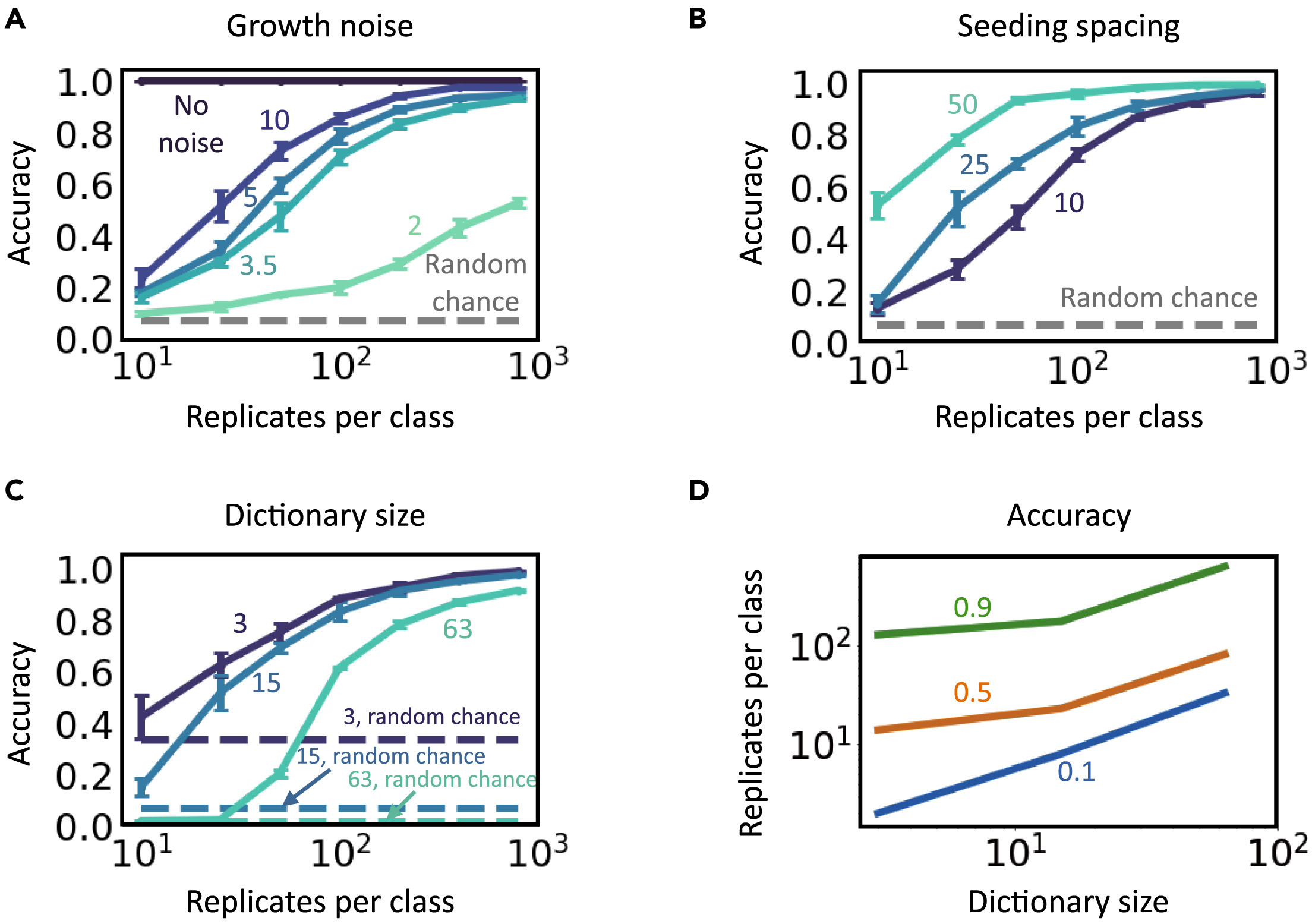
Изображение №2

Степень и безопасность кодирования также может модулироваться путем настройки шума в процессе формирования паттерна. Без шума одного паттерна на входе достаточно для идеального декодирования, если выходные паттерны различимы (2A).

Слишком много шума внесет слишком много вариаций в повторяющиеся паттерны, генерируемые каждым входом. Если эти внутрикатегориальные вариации (между повторяющимися паттернами) приближаются или превышают межкатегориальные различия (между наборами паттернов, соответствующих разным входным данным), точность декодирования значительно ухудшится (2A). В зависимости от величины шума эту потерю точности можно уменьшить, увеличив количество повторяющихся паттернов на класс.

Аналогичный компромисс существует и для других параметров, таких как расстояние между точками в исходной конфигурации (2B). Когда расстояние уменьшается, узоры, выращенные из разных конфигураций, кажутся более похожими и неразличимыми. Кроме того, больший словарь при прочих равных также снизит точность декодирования (2C). Опять же, увеличение количества повторяющихся паттернов на класс может компенсировать потери в точности, тем самым увеличивая емкость кодирования (2D).

Как объясняют ученые, схема кодирования-декодирования применима к любым динамическим системам, где отображение ввода-вывода удовлетворяет перечисленным выше критериям. Чтобы проиллюстрировать этот момент, ученые выбрали элементарную CA модель со слабо хаотической динамикой.

Учитывая набор правил, были выбраны параметры модели (включая уровни шума) таким образом, чтобы результирующая динамика могла обеспечить безопасное кодирование и надежное декодирование. Символы кодировались в двоичный код, который затем преобразовывался в начальную 1D и 2D конфигурацию. Шум был наложен на исходную последовательность, и та превращалась в окончательную последовательность в соответствии с правилами. Нейронная сеть с прямой связью была обучена кодировать окончательную последовательность. Как и ожидалось, более высокая сложность приводит к ухудшению точности декодирования, но это можно исправить, увеличив размер обучающих данных.


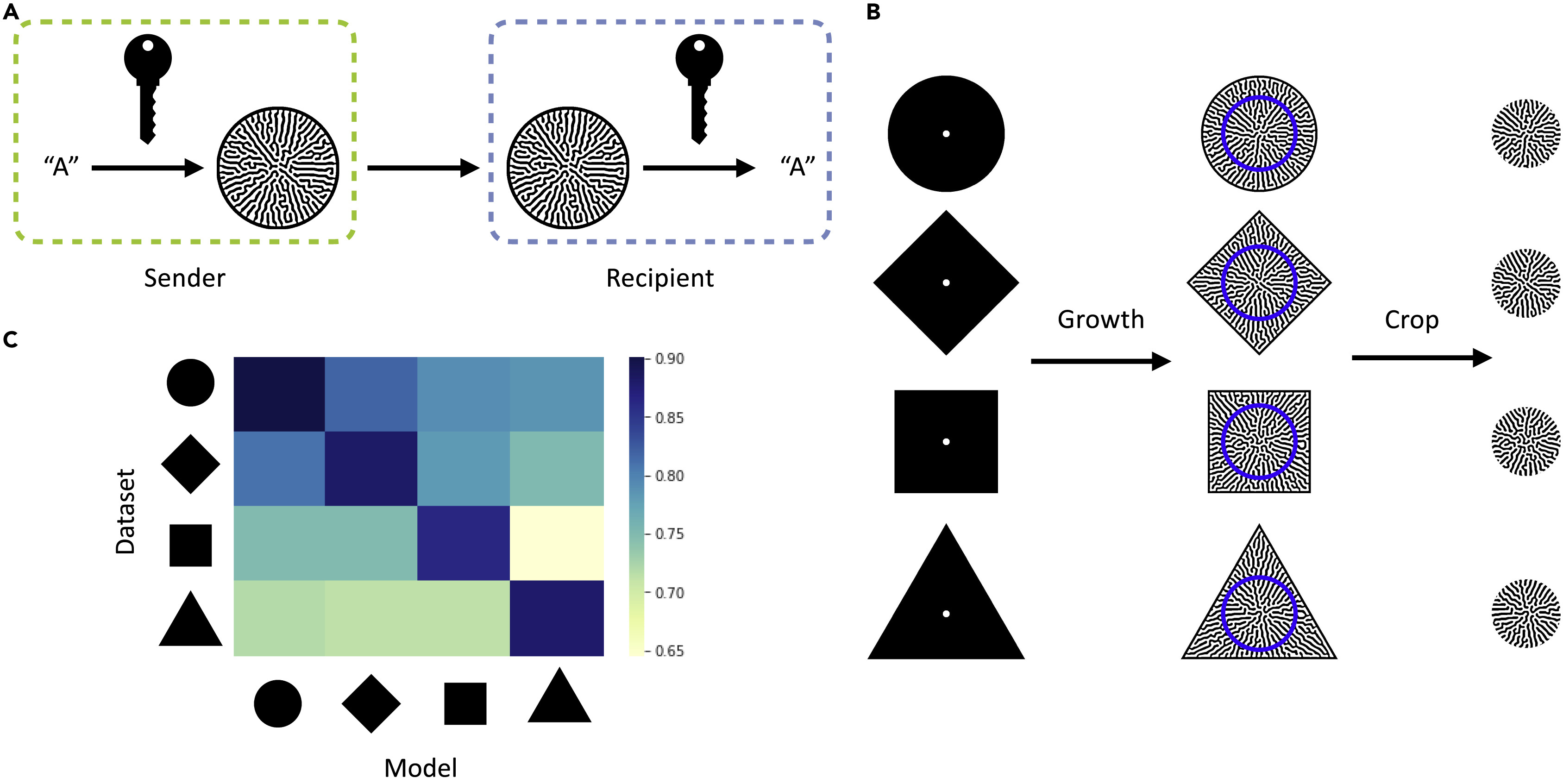
Изображение №3

Для повышения безопасности ученые решили применить шифрование, дабы предотвращать несанкционированный доступ к информации во время ее передачи. Секретный ключ реализовывался во время кодирования, а для успешного декодирования, соответственно, требовался правильный ключ (3A).

Для систем формирования паттерна геометрия домена паттерна является возможным выбором секретного ключа, поскольку она может влиять на процесс паттерна и легко настраивается.

В изучаемой системе основной акцент это бактерии, их рост и распространение. Другими словами, распространение колонии. Это распространение может быть ограничено физически посредством границ (например, бактерии растут только внутри чаши Петри). Изменение этих границ позволяет зашифровать паттерн внутри определенной формы. Чтобы на практике проверить данную теорию, ученые сгенерировали набор паттернов внутри разнообразных форм. Для каждой формы результирующие паттерны занимают все пространство. Затем из входных данных кодирования была удалена информация о границах формы. Для этого использовались лишь центральные области паттерна (3B).

И тут выяснился любопытный факт — лишь те декодеры, которые владели полной информацией, достигали высокой точности декодирования (3C). Это значит, что им была необходима информация об изначальной форме границ, внутри которых рос бактериальный паттерн. Следовательно, форма границ служила своеобразным секретным ключом для успешного декодирования.

При прочих равных надежность декодирования можно повысить, увеличив количество повторов на класс при обучении декодера. Однако степень улучшения уменьшается для увеличения числа повторов (2C).

Например, для словаря из 63 символов точность декодирования увеличивается в 30 раз при увеличении числа повторов с 10 до 100, но лишь в 1.5 раза при увеличении со 100 до 800. Чтобы более эффективно использовать имеющиеся данные, ученые применили ансамбль методов, когда применяется сразу несколько методов машинного обучения.


Изображение №4

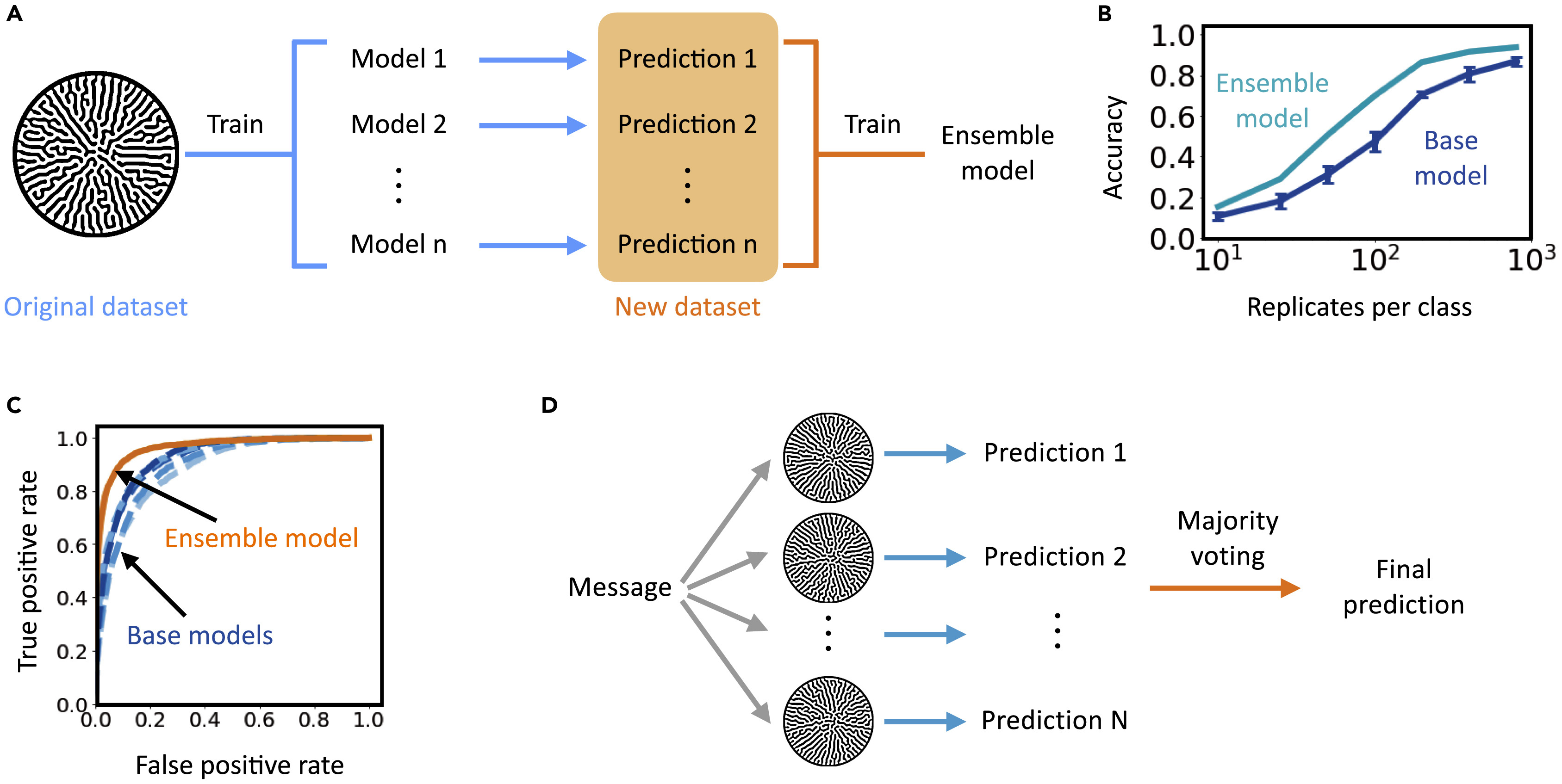
Утрировано говоря, первым делом CNN декодеры обучались на наборе данных со случайной инициализацией. Потом полученные результаты обучения становились новым набором данных, который использовался для обучения ансамблевого декодера (4A).

Для паттернов, сгенерированных с умеренным шумом, производительность прогнозирования ансамблевого декодера превосходит базовые модели в точности на 22% (4B).

ROC-кривая (рабочая характеристика приемника) и матрица несоответствий также показали значительное улучшение точности при использовании ансамблевой модели (4C). Также было показано, что помимо ансамблевой модели метод голосования может улучшить точность декодирования (4D). Несколько паттернов, соответствующих одному и тому же символу, были декодированы с использованием одной и той же CNN, и прогноз, получивший наибольшее количество голосов, использовался в качестве окончательного.


Изображение №5

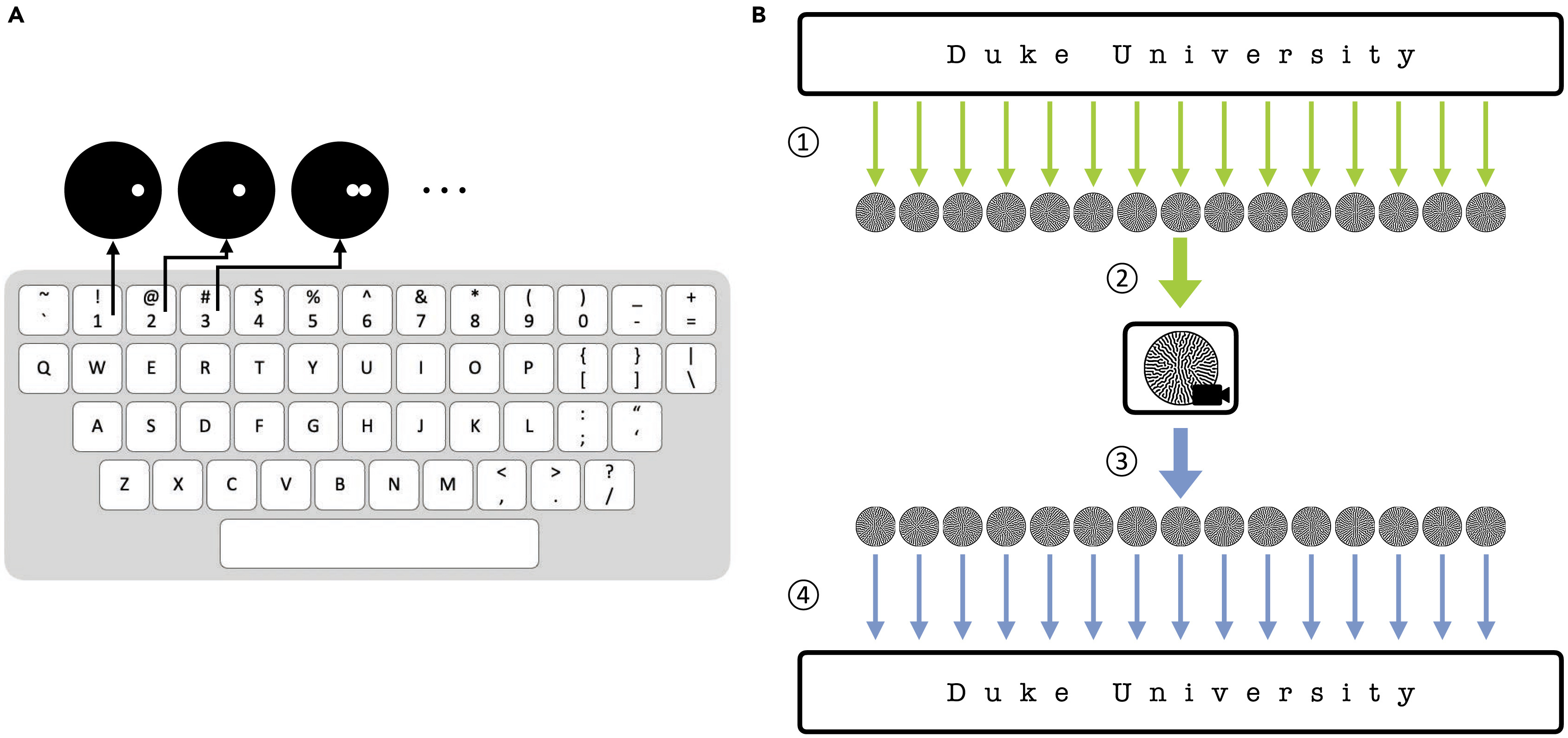
В завершение ученые решили провести более демонстративный практический опыт. Было создано 100 наборов паттернов для кодирования всех ASCII символов, включая буквы (строчные и прописные), цифры, знаки препинания и пробел (5A). Для создания обучающего набора данных использовался 7-битный массив заполнения, в котором 100 уникальных начальных конфигураций соответствовали символам. Каждая из первоначальных конфигураций затем использовалась для создания 1000 паттернов. Данный набор паттернов, названный учеными «Emorfi», представляет собой новую схему кодирования, сгенерированную цифровым способом.

При кодировании текста каждый символ представляется одним или несколькими сгенерированными шаблонами с одинаковыми настройками, а затем паттерн компилировался в целостное видео (5B).

Для примера ученые закодировали текст выступления Мартина Лютера Кинга «У меня есть мечта», содержащее 8869 отдельных символов.

Видео №1: закодированное выступления Мартина Лютера Кинга «У меня есть мечта».

Используя методику голосования, каждый символ можно было представить пятью различными паттернами, и 99.8% текста можно было правильно декодировать.

Тот же подход был также использован для кодирования стихотворения Уильяма Блейка «Знамения невиновности», и 99.6% текста было правильно декодировано.

Видео №2: закодированный стих Уильяма Блейка «Знамения невиновности».

Видео №3: закодированная последовательность белка GFP (238 аминокислот), 100% было успешно декодировано.

В вышеперечисленных примерах попытки несанкционированного доступа к данным невозможны, так как потенциальный злоумышленник не имеет доступа ко всему обучающему набору данных, который использовался системой кодирования. К примеру, имея доступ к 10 паттернам на класс, взломщик сможет декодировать лишь 1.3% закодированного стиха Уильяма Блейка.

Для более детального ознакомления с нюансами исследования рекомендую заглянуть в доклад ученых и дополнительные материалы к нему.

Эпилог

Отрасль шифрования данных находится в процессе постоянного развития, как и отрасль взлома. Это можно назвать своеобразной соревновательной эволюцией, когда более надежный шифр порождает новый тип взлома, а новый тип взлома стимулирует появление еще более надежного шифра.

По сути, главным оружием кодирования является непредсказуемость, уникальность и большой набор вариантов. И бактерии могут это дать. К примеру, возьмем какую-то бактерию и поместим ее в 10 отдельных чаш Петри. Условия для развития колоний, как и сама бактерия, одинаковы, но результирующий паттерн клеток внутри каждой из чаш будет уникален. Невооруженному глазу может показаться, что паттерны в некоторых из чаш одинаковы, но детальное рассмотрение покажет, что это не так.

Авторы рассмотренного нами сегодня труда использовали эту бактериальную уникальность для кодирования информации. Разработанная ими система, использующая сверточные нейронные сети, после обучения могла зашифровывать сообщение в виде видео, состоящего из последовательного набора паттернов. Дабы декодировать сообщение, необходимо знать все исходные условия, в том числе и то, в емкости какой формы развивалась колония бактерий.

Испытать систему кодирования-декодирования можно самостоятельно, перейдя по ссылке. Чуть ниже описания системы есть поле, в котором вы можете ввести текст (только на английском), а система выдаст вам зашифрованный вариант в виде видео, который вы потом можете дешифровать, используя ту же систему.

Немного рекламы

Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).

Dell R730xd в 2 раза дешевле в дата-центре Maincubes Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?