Система противораскачивания груза (Anti-Sway Control) / forpes.ru

Главная
Система противораскачивания груза (Anti-Sway Control)

Система противораскачивания груза (Anti-Sway Control) +31

22.03.2023 09:11

LanaVeryatinskaya 61 2700 Источник

В сфере грузоподъемной техники система противораскачивания довольно популярная и полезная штука. Эта система полезна тем, что, к примеру, оператор крана не обязан корректировать движение крана самостоятельно, чтобы не происходило раскачивание груза и не было рисков возникновения аварийных ситуаций. Многие производители предлагают свои системы на базе ПЛК (программируемых промышленных контроллеров) либо на базе ПЧ (преобразователей частоты). Мы в нашем инженерном центре тоже решили не стоять в стороне и делать свою систему. Погружение в теорию привело нас к пространству состояний. Таким образом целью статьи является рассказать, как возможно решить задачу противораскачивания груза в пространстве состояний.

Постановка задачи: прийти в заданную позицию за наименьшее количество времени, не превышая доступную скорость и без раскачивания груза. Все ограничения взяты из характеристик стенда, для которого производятся расчеты.

Обозначения

M = 30 кг – масса тележки

m = 10 кг – масса груза

f – сила, прикладываемая к тележке

x(t) – значение горизонтального перемещения тележки

α – угол поворота маятника, учитывается в положительном направлении от строго вертикального положения вниз

l = 1.2 м – расстояние от точки крепления до
центра масс маятника

Дифференциальные уравнения

Первым шагом нужно представить модель в математическом виде. Для того, чтобы перейти в пространство состояний, нужно записать модель в виде дифференциальных уравнений первого порядка. Но обо всем по порядку.

Начнем с дифференциальных уравнений. Чтобы представить модель в таком виде мы воспользуемся методом Лагранжа.

Метод Лагранжа

Данный метод позволяет написать дифференциальные уравнения движения второго порядка. Суть метода заключается в том, что динамика механической системы рассматривается в целом и внутренние силы реакции связей исключаются из уравнений модели. Чтобы записать модель, нужно выбрать обобщенные координаты и обобщенные скорости. Что это такое? Обобщенные координаты – это независимые друг от друга параметры, которые определяют положение системы в пространстве, а обобщенные скорости это их производные. В нашей модели это позиция тележки и угол поворота маятника и, соответственно, их производные это скорости.

После того, как мы определились с нужными параметрами, можем перейти к уравнениям.

Уравнение Лагранжа имеет вид:

Обозначения

Функция Лагранжа или Лагранжиан вычисляется как:

Обозначения

Т - кинетическая энергия

U - потенциальная энергия

Разобрались с теорией, перейдем к нашей системе. Начнем с функции Лагранжа, для этого необходимо найти потенциальную и кинетическую энергии всей системы.

Потенциальная энергия этой системы определяется только потенциальной энергией отклонённого на угол маятника. Тележка находится на поверхности, которая является нулевым уровнем относительно нее, поэтому высота равняется нулю и, соответственно, потенциальная энергия тоже равна нулю.

Вывод уравнения кинетической энергии системы

Полная кинетическая энергия состоит из кинетических энергий поступательного движения тележки и движения центра масс маятника.

$T=\frac{1}{2} Mv^2+\frac{1}{2} mv^2=\frac{1}{2} M\dot{x}^2_c+\frac{1}{2} m(\dot{x}^2_p+\dot{y}^2_p)$

Необходимо выразить координаты центра масс маятникачерез координаты тележки:

Нужны скорости, поэтому продифференцируем эти два уравнения:

$\dot{x_p}=\dot{x}_c+l\dot{α}cosα$ $\dot{y}_p=l\dotαsinα$

Подставляем в формулу кинетической энергии:

$T=\frac{1}{2} M\dot{x}^2_c+\frac{1}{2} m(\dot{x}^2_c+2\dot{x}_cl\dot{α}cosα+l^2\dot{α}^2)$

Полная кинетическая энергия системы:

$T=\frac{1}{2} M\dot{x}^2_c+\frac{1}{2} m(\dot{x}^2_c+2\dot{x}_cl\dot{α}cosα+l^2\dot{α}^2)$

Все найденное подставляем в формулу Лагранжиана и получаем:

$L=\frac{1}{2} M\dot{x}^2_c+\frac{1}{2} m(\dot{x}^2_c+2\dot{x}_cl\dot{α}cosα+l^2\dot{α}^2)-mgl(1-cos⁡α)$

Теперь можно составить систему уравнений Лагранжа нашей системы. Первое уравнение будет описывать движение тележки. Так как это движение линейное, воздействием является сила. Второе уравнение – движение маятника, воздействием является момент. Маятник совершает свободные колебания и не управляется никаким приводом, поэтому момент равен нулю:

Подставив все, продифференцируем и получим систему уравнений:

Линеаризация

Система нелинейная и надо это исправить, потому что иначе не выйдет далее перейти к нормальной форме Коши. При достаточно малых значениях можно заменить нелинейные функции, как первые члены ряда Тейлора: $\dot{α}^2≈0$ .

Тогда упрощённая система будет выглядеть так:

Итоговые уравнения

Дальше мы приведем эти уравнения к нормальной форме Коши. Это система дифференциальных уравнений первого порядка, в которой производная в левой части, а все остальное в правой части уравнения. После некоторых преобразований получим два уравнения.

Последним шагом является ввод вектора состояния:

где - позиция тележки, - угол поворота маятника, $\dot{x}(t)$ - скорость тележки, $\dot{α}(t)$ - скорость угла поворота маятника. Такой вектор выбран относительно составляющих уравнений и будущих желаемых результатов.

Теперь можно перевести систему в пространство состояний. В пространстве состояний удобнее работать со всеми состояниями, в отличии от остальных видов представления математических моделей.

Пространство состояний

Пространство состояний – n-мерное пространство, которое состоит из элементов, каждый из которых полностью определяет состояние рассматриваемой системы.

Описывается система двумя векторно-матричными уравнениями.

1. Дифференциальное уравнение состояния:

$\dot{x}=Ax(t)+Bu(t)$

Обозначения

Это уравнение линейного объекта отражает его динамические свойства и записывается в виде векторного дифференциального уравнения в форме Коши.

2. Дифференциальное уравнение выходов:

Обозначения

Это уравнение связывает переменные состояния и управляющие воздействия с выходными измеряемыми переменными.

Модель в пространстве состояний будет выглядеть так:

$A =\begin{bmatrix} 0&0&1&0\\0&0&0&1\\0&\frac{gm}{M}&0&0\\0&-\frac{g(M+m)}{Ml}&0&0\end{bmatrix}; B=\begin{bmatrix} 0\\0\\\frac{1}{M}\\-\frac{1}{Ml}\end{bmatrix};$ $C=\begin{bmatrix} 1&0&0&0 \\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}; D=\begin{bmatrix} 0 \\ 0\\0\\0 \end{bmatrix};$

В полученном виде можно подавать любое усилие на систему и наблюдать за поведением тележки. Однако, в реальной жизни, тележка управляется заданием скорости и так как нас интересует не усилие, которое необходимо, чтобы сдвинуть тележку с заданной скоростью на заданное расстояние, а то как будет раскачиваться груз при заданном движении, модель необходимо перевести к такому виду, чтобы входными воздействием у нас являлась скорость.

Модель тележки с грузом с управлением по скорости

Так как нет конкретного способа преобразовать силу в скорость, были выполнены преобразования.

Преобразования силы в скорость

Если представить модель упрощённо, то система выглядит таким образом:

F – заданная сила (входное воздействие)

G – объект моделирования

V – скорость тележки (выходное состояние)

Обратившись ко второму закону Ньютона и представив формулу в виде структурной схемы, в которой выход будет скорость.

Для того, чтобы на вход подавалась скорость, необходимо добавить обратную связь и регулятор (коэффициент усиления), который будет преобразовывать заданную скорость в силу.

Записав передаточную функцию системы получим:

$W_{зам}=\frac{K_1}{s+K_1}$

Получилось апериодическое звено. Его переходная характеристика является плавно возрастающей или убывающей и достигается заданное значение. Это означает, что такой прием можно использовать в нашем случае для выражения скорости.

V*– заданная скорость (входное воздействие)

K₁ – коэффициент усиления

G – объект моделирования

V- фактическая скорость (выходное состояние)

Коэффициент K₁ отображает скорость отработки тележкой заданной скорости. Для будущих расчетов примем примерно K₁ =500.

Из полученной модели выразим силу, для того, чтобы заменить ее в дифференциальных уравнениях.

Так у нас получилось вывести нужные дифференциальные уравнения и матрицы пространства состояний.

Дифференциальные уравнения

Матрицы пространства состояния

$A =\begin{bmatrix} 0&0&1&0\\0&0&0&1\\0&\frac{gm}{M}&-\frac{K_1}{M}&0\\0&-\frac{g(M+m)}{Ml}&\frac{K_1}{Ml}&0\end{bmatrix}; B=\begin{bmatrix} 0\\0\\\frac{K_1}{M}\\-\frac{K_1}{Ml}\end{bmatrix};$ $C=\begin{bmatrix} 1&0&0&0 \\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}; D=\begin{bmatrix} 0 \\ 0\\0\\0 \end{bmatrix};$

Выбор регулятора

Теперь перейдем к главному вопросу – как задать нужное управление. Для этого нам понадобится регулятор. Определить вид регулятора нужно исходя из требований и формы представления математической модели. Наша модель представлена в виде пространства состояний, поэтому, чтобы влиять на все состояния по отдельности, необходимо найти матрицу, с помощью которой будет обеспечиваться устойчивый процесс управления. Таким образом формируется многомерная система управления, реализующая принцип обратной связи. У нас частный случай и управляющее воздействие одно.

Выбор пал на модальный регулятор, т.к. с его помощью есть возможность обеспечивать для замкнутой системы требуемое расположение полюсов. Корни (полюса) - это корни характеристического полинома матрицы состояния А. Корни характеризуют поведение системы, какими качествами она будет обладать (перерегулирование, время регулирования и т.д.).

Ввод регулятора K в систему преобразует управляющее воздействие к виду: . Подставив управляющее воздействие в уравнение состояния получим: $\dot{x}=(A-BK)x$ . Таким образом регулятор K будет напрямую влиять на расположение полюсов матрицы состояния и тем самым влиять на поведение системы.

Синтез регулятора

Синтез модального регулятора состоит в выборе параметров регулятора. Для синтеза регулятора необходимо определить, является ли система полностью управляемой.

Если система управляема, то значит можно найти такое управление, чтобы перевести систему из начального в конечное состояние.

Для нашего случая ручные вычисления очень трудоёмкие, поэтому расчет проведен в среде Matlab при помощи команды ctrb(A,B), которая рассчитывает матрицу управляемости. Система полностью управляема. Значит можно начать синтез регулятора.

Алгоритм расчета параметров модального регулятора

Существует алгоритм расчета коэффициентов для модального регулятора. Он был взят из источника.

Проводить каждый раз расчет параметров вручную нецелесообразно, воспользуемся функцией acker в Matlab. В основе работы функции лежит данный метод расчета.

Команда K = acker (A, B, P) вычисляет такую матрицу K, что полюса системы A-BK равны значениям, заданным вектором желаемых полюсов P.

Теперь стоит вопрос в том, какие задавать желаемые полюса (корни).

Выбор корней

Напомним, что корни (полюса) - это корни характеристического полинома матрицы состояния А. Корни характеризуют поведение системы, какими качествами она будет обладать (перерегулирование, время регулирования и т.д.). Желаемые корни это те, которые мы хотим получить в результате работы регулятора. Основной критерий для устойчивости системы: корни характеристического полинома должны лежать в левой комплексной полуплоскости.

Подбор корней для решения задачи движения по положению

Для начала попробуем выбрать корни, которые будут обеспечивать движение по заданному положению. Схема собрана в Simulink:

В данной схеме входными воздействиями являются заданные состояния системы в таком порядке: позиция тележки, угол маятника, скорость тележки, скорость угла поворота маятника. В примере на первый вход (позиция тележки) задается 2 м, а на остальные входы подаются 0.

Расчет коэффициентов регулятора, как и было сказано, будет в Matlab.

Для примера выберем вектор полюсов [-1 -1 -1 -1].

Коэффициенты регулятора: K=[0.0073 0.3616 -0.9706 -0.2528]

Система отработала относительно хорошо. Нет перерегулирования по положению и система без ошибки пришла в заданную позицию, также она устойчива, благодаря отрицательным корням. При увеличении значений корней тележка приходит в заданную позицию быстрее, но график скорости может ухудшаться, ее поведение не может быть удовлетворительным в реальных условиях.

Пример с корнями [-3 -3 -3 -3]

Коэффициенты регулятора: К = [0.5945 -2.3898 -0.2073 0.0872]

При векторе желаемых корней [-3 -3 -3 -3] переходная характеристика скорости тележки имеет сильные колебания, что неудовлетворительно для работы в реальной жизни.

Но у нас стоит задача задавать скорость и позицию тележки.

Выбор корней для решения задачи движения с заданной скоростью и в заданную позицию

Для решения поставленной задачи необходимо на вход задавать и желаемое положение, и желаемый закон скорости. Для этого был создан блок Speed generator. Этот блок генерирует кривую разгона, которая позволяет двигаться с желаемыми временем ускорения и замедления, скоростью и расстоянием.

Внутри устанавливается позиция, скорость и время разгона.

Добавим новый блок Speed generator в нашу схему.

Необходимо выбрать требования, которые могут показать наиболее приближенный результат к реальным условиям. Мы будем проверять результаты при входных значениях: позиция 1 м и скорость тележки 0,28 м/с (номинальная скорость для стенда).

Стоит следующая задача: тележка должна прийти в заданную позицию за наименьшее время, график скорости должен быть как можно ближе к заданному закону, система устойчива. Но подбирать корни снова вручную плохой вариант, потому что неизвестно, какой набор корней из множества вариантов будет лучший. Поэтому нужно найти алгоритм, в котором можно было бы учитывать качества системы.

При поиске методов мы столкнулись с тем, что источников информации очень мало, многие методы подбора корней основываются на ручном подборе. Нам необходимо, чтобы можно было учитывать будущее поведение переходных характеристик. Был найден один приблизительный алгоритм в источнике.

Алгоритм расчета корней

1. Определить порядок системы, следовательно степень характеристического полинома.

2. Выбрать стандартный полином для последующих расчетов: полином Ньютона или полином Баттерворта. Выбор исходит от требований к показателям качества будущей переходной характеристики. Если требуется, чтобы не было перерегулирования, то выбирается полином Ньютона, т.к. корни его полиномов вещественные и не имеют мнимой части, которая влияет на перерегулирование. Если перерегулирование больше 1%, то выбирается полином Баттерворта, т.к. корни его полинома имеют мнимые части. Значения перерегулирования и времени регулирования можно посмотреть в таблице 1 и 2.

3. Выбрав из таблицы 1 или 2 значение времени регулирования по номеру порядка системы и желаемое время регулирования, данные подставляются в формулу для вычисления ω₀– радиуса окружности, на котором лежат полюса.

$ω_0=\frac{t_п^1}{t_п}$

t¹_п - время регулирования стандартного полинома

t_п - желаемое время регулирования

ω₀ - радиус окружности

4. Далее полученное значение подставляется в выбранный полином и рассчитываются коэффициенты этого полинома, потом надо найти его корни. Это и будут желаемые корни, которые далее используются для нахождения параметров модального регулятора.

Таблица 1 - Показатели качества полинома Ньютона

Порядок полинома	1	2	3	4	5	6
Время регулирования t¹_п, с	3,0	4,8	6,3	7,8	9,2	10,5
Перерегулирование σ, %	0	0	0	0	0	0

Таблица 2 -Показатели качества полинома Баттерворта

Порядок полинома	1	2	3	4	5	6
Время регулирования t¹_п, с	3,0	2,9	6,0	6,8	7,7	10,8
Перерегулирование σ, %	0	4,5	8,0	11,0	13,5	14,3

Зададим динамические показатели качества: перерегулирование σ = 0% и время переходного процесса будем подбирать вручную, подставляя в формулу. Для дальнейшего расчета выберем характеристический полином Ньютона, т.к. он соответствует перерегулированию равному 0 %. Объект управления обладает четвертым порядком. Выберем полином 4 порядка.

Как сказано в алгоритме, для расчета корней необходимо задаться временем переходного процесса, который значительно влияет на поведение системы. Методом подбора выбрали время равное 2 с. Если брать значение больше или меньше, характеристики переходных процессов не удовлетворяют поставленным требованиям. Для разных параметров системы это время будет свое.

$ω_0=\frac{7.8}{2}=3.9$

Получаем значение радиуса окружности, на которой будут располагаться корни, и подставляем в полином. Находим корни полинома, они и будут нашими желаемыми корнями. На основе этих корней рассчитываем параметры регулятора. С полученными параметрами переходные характеристики системы выглядят следующим образом:

Коэффициенты регулятора: K=[1.6979 -3.7484 0.7415 0.9666]

Если опираться на переходную характеристику скорости тележки, этот вариант наиболее приемлемый, т.к. есть относительно продолжительный участок, где тележка едет с постоянной заданной скоростью. Также важно, что значение не превышает доступную скорость. Остальные характеристики тоже удовлетворяют всем требованиям, маятник не раскачивается, тележка едет плавно к заданной позиции.

В результате удалось сформировать управление перемещением крана без раскачивания груза, удовлетворяющее условиям (прийти в заданную позицию за наименьшее количество времени, не превышая доступную скорость и мощность).

Светлана Верятинская

Инженер-разработчик ООО "Троицкий крановый завод"

Статья написана в соавторстве с @ivpo6 (инженер-программист Иван Попков)

Комментарии (61)

ValeriyS
00.00.0000 00:00
#25356350
+6
Круто. К сожалению не могу поделиться предложенным мной подходом к линеаризации - это интеллектуальная собственность компании, где я работаю.

Вместо полинома лучше использовать разложение частотной характеристики объекта управления на биквадратные секции. Тогда контроллер можно строить как инверсию нулей в полюса и наоборот. Кроме того, биквадратное предсталение (SOS в Матлабе) позволяет решить проблему стабильности вычислений.
1. LanaVeryatinskaya Автор
  00.00.0000 00:00
  #25360350
  Расскажите, пожалуйста, о данном методе. Возможно можете посоветовать литературу?
  1. ValeriyS
    00.00.0000 00:00
    #25361536
    +1
    Я плохо знаю терминологию на русском языке в этой предметной области, так что не судите строго :)
    
    Если система существенно нелинейна, то нет особого смысла говорить о нулях и полюсах или о частотной характеристике, поэтому далее я предполагаю, что система уже линейна.
    
    В Матлабе есть функция преобразования State Space модели (A,B,C,D) в SOS - ss2sos. SOS модель можно импортировать и визуализировать в fvtool. Основной смысл SOS - разбить полином на более простые элементы, делая процесс вычислений устойчивым и предсказуемым. Реализация вычислений с помощью SOS секций на PC или FPGA особых затруднений не вызывает.
    
    State Space модель может также быть конвертирована в zero/pole/gain модель. Это позволяет построить идеальный feedback контроллер путём использования в контроллере полюсов на местах нулей объекта и нулей на местах полюсов. Добавив в котнтроллер интегратор получаем идеальный feedback контроллер. Это справедливо, конечно, если наш объект (plant) является минимально-фазовой системой, т.е. не имеет нулей вне единичной окружности.
    
    Попробуйте поискать литературу по ключевым словам типа "book Digital Signal Processing MATLAB". Наверняка и на русском языке это есть, может кто ещё из читающих эту тему вам посоветует.
    
    Arastas
    00.00.0000 00:00
    #25361666
    Это, по сути, синтез по желаемой ЛФЧХ. Но не стоит так делать в системах, где ожидается парирование регулятором возмущений - там сокращения нулей/полюсов может не произойти. ;)
    
    ValeriyS
    00.00.0000 00:00
    #25361744
    Не очень понял ваш комментарий, но наверно вы говорите о System Identification. Это случай, когда мы измерили АЧХ и ФЧХ объекта и хотим представить его в виде набора нулей/полюсов. Тогда, конечно, полной компенсации за счет взаимного уничтожения нулей/полюсов не получится. В данной статье другой случай. У нас есть аналитическое выражение для State Space, котрое мы можем аналитически-же разложить на нули/полюса и построить совершенно идеальный feedback контроллер.
    
    Чаще всего модель заметно отличается от реальной системы, но в данной статье, по-моему, рассматривается идеализированный точный вариант.
    
    Arastas
    00.00.0000 00:00
    #25362128
    Я хотел сказать, что описанная вами процедура в советской литературе, как мне кажется, более всего соответствует синтезу по желаемым ЛАФЧХ.
    
    konusnyj_flexer
    00.00.0000 00:00
    #25362398
    Не совсем понял про " мы можем аналитически-же разложить на нули/полюса и построить совершенно идеальный feedback контроллер". Насколько я понимаю, данная система в пространстве состояний может быть представлена в виде четырех (по количеству состояний) передаточных функций с полюсами и нулями, где входом будет задание силы/скорости, а выходом одна из переменных состояния. И Вы имеете в виду, что к каждой это передаточной функции можно было бы сделать "идеальный feedback контроллер"? Ну пусть не к каждой, а, например, к двум, которые интересуют: угол и позиция/скорость
    
    ValeriyS
    00.00.0000 00:00
    #25365118
    Если мы имеем систему с несколькими степенями свободы (например угол/позиция) и таким же количеством наших элементов воздействия, то сначала надо выполнить decoupling. После этого можно управлять независимо по каждой из степеней свободы. Decoupling - отдельная большая тема, я не хотел бы смешивать всё в одном флаконе :)
    
    Если я понял правильно, здесь мы имеем систему с одним элементом воздействия. Далее не важно, сколько внутренних переменных состояния имеет наш объект, т.к. для линейной системы у нас будет только одна АЧХ/ФЧХ. Если мы знаем полином для этой ЧХ, то можем разложить полином на нули/полюса и так далее.
    
    LanaVeryatinskaya Автор
    00.00.0000 00:00
    #25362126
    Очень интересно, обязательно почитаю и попробую. Спасибо большое!

ggoy
00.00.0000 00:00
#25356812
А без линеаризации уравнений эту задачу можно пытаться решать?
1. LanaVeryatinskaya Автор
  00.00.0000 00:00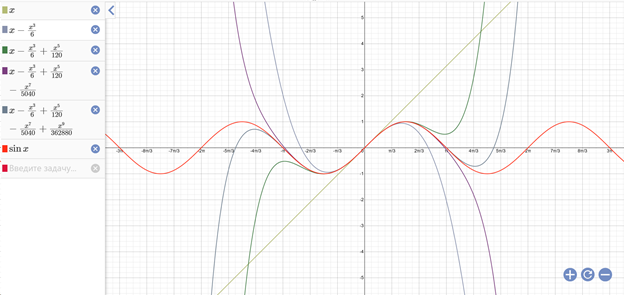
  #25356868
  Без линеаризации не получится решить данную задачу. По поводу углов, можете посмотреть, к примеру, на график разложения синуса в ряд Тейлора. Из рисунка видно, что до значения pi/6 угол отклонения можно считать малым. В нашем случае получилось 2 градуса.
  1. Arastas
    00.00.0000 00:00
    #25357618
    Вы считаете, что у стандартной задачи маятника на тележке нет нелинейных регуляторов?
    
    LanaVeryatinskaya Автор
    00.00.0000 00:00
    #25358694
    Нет, просто вопрос был переформулирован и ответ выглядит некорректно. Имелось в виду, чтобы записать модель в пространстве состояний нужно было провести линеаризацию.
    
    Arastas
    00.00.0000 00:00
    #25358724
    Нормально нелинейные системы пишутся в пространстве состояний, $\dot x = f(x,u)$ это тоже пространство состояний. А вот для записи в линейной форме надо линеаризировать.
    
    konusnyj_flexer
    00.00.0000 00:00
    #25359288
    А разве на основе нелинейной записи в пространстве состояний можно потом придти к какому-то регулятору, синтезировать его и найти параметры? Думал для того и линеаризуют, чтобы разработать регулятор, так как математика, вроде бы, с линейными системами гораздо лучше умеет обращаться
    
    Arastas
    00.00.0000 00:00
    #25359314
    Линейные системы проще, и линеаризованных систем в большинстве случаев достаточно. В остальных случаях приходится работать с нелинейностями.
    
    konusnyj_flexer
    00.00.0000 00:00
    #25359826
    А не могли бы Вы привести пример такого регулятора? Это как если бы тележка могла развивать только максимальную (в обе стороны) скорость или стоять на месте?
    
    Arastas
    00.00.0000 00:00
    #25360016
    Это вы имеете ввиду sliding mode? Раз у вас управление это сила, то именно она должна принимать крайние значения, а не скорость.
    А вообще надо смотреть литературу по cart-pendulum nonlinear control. Там наверное и какие-то feedback linearization есть, backstepping.
    
    konusnyj_flexer
    00.00.0000 00:00
    #25360114
    Ну вообще там в статье есть описание перехода от модели по силе к модели по скорости (через просто пропорциональный регулятор), так как реальной тележкой контроллер управляет все же по скорости. Поэтому и написал про скорость.
    
    Да, sliding mode тоже первым в голову пришел, но думал может еще какие есть.
    
    Спасибо за рекомендацию по литературе
1. Refridgerator
  00.00.0000 00:00
  #25358298
  Можно, если использовать современную элементную базу и управлять процессами программно. Можно даже не лезть глубоко в математику — можно просто численно промоделировать все эти процессы и подобрать параметры экспериментально. Нули и полюса, о которых говорится в статье, нужны только для аналитического расчёта аналоговых стандартных фильтров и разбиения их на элементарные компоненты. В цифре об этом можно вообще не париться.
  1. KanSergo
    00.00.0000 00:00
    #25358778
    Не очень понял, почему в цифре можно об этом не париться? Можно поподробнее? Есть какие-то примеры подобного подхода?
    
    Refridgerator
    00.00.0000 00:00
    #25358910
    Ну потому что в цифре частотную и/или фазовую характеристику можно нарисовать произвольную и аппроксимировать с любой точностью и необходимыми ограничениями, а импульсную характеристику получить через FFT, а реализовать через быструю свёртку. Пример такого подхода — управление электродами в дуговой электросталеплавильной печи, где цена резонанса в разы выше перевозки грузов.
    
    ValeriyS
    00.00.0000 00:00
    #25360360
    Я тоже так думал, пока не пришлось реализовывать систему с обратной связью (feedback control, FBC). Для FBC принципиально иметь минимальную задержку в петле обратной связи, поэтому FIR, FFT и прочие прелести сильно вредят устойчивости. Гораздо больший запас по фазе получается в цифровыми фильтрами типа IIR. Что касается аналоговых фильтров, то им соответствуют биквадратные цифровые IIR фильтры (Second Order Section, SOS).
    
    Refridgerator
    00.00.0000 00:00
    #25360448
    Так есть реализация FIR вообще без задержек, и в устойчивости они наоборот в приоритете. Также есть алгоритмы для преобразования произвольных фильтров с линейной фазой к каузальному виду, то есть минимизирующих задержку отклика к максимально возможной, пересчитывая фазы в зависимости от амплитуд. IIR же не зря разбивают на биквады — потому что даже на не особо больших порядках они очень быстро теряют численную устойчивость. А у FIR таких проблем нет по определению.
    
    ValeriyS
    00.00.0000 00:00
    #25360684
    FIR без задержек должен не иметь нулей на единичной окружности или вне её. Т.е. он фактически превращается в комбинацию минимально-фазовых SOS IIR фильтров. Поэтому не умаляя общности можно говорить, что всё реализовано на IIR фильтрах.
    А вообще хотелось бы посмотреть на ваш пример FIR фильтра, который при заданной амлитудной частотной характеристике имеет такую же минимальную задержку, что и минимально-фазовый IIR фильтр :)
    
    Refridgerator
    00.00.0000 00:00
    #25360876
    FIR без задержек ничего не знает про нули. Это просто комбинация прямой реализации со сложностью O(n^2) и быстрых реализаций со сложностью O(log(n)) опираясь на тот факт, что свёртку можно распараллелить. Хотите больше конкретики — ну так давайте конкретную АЧХ, сделаем оба варианта.
    
    ValeriyS
    00.00.0000 00:00
    #25361436
    Пример минимально-фазового IIR фильтра 2-го порядка (Fs = 48 kHz):
    
    Numerator:
    0.56999999999999995115018691649311222136
    -0.208009478672987219161072403039725031704
    0.064150573886480918850416799159575020894
    Denominator:
    1
    -1.553554502369669521044670545961707830429
    0.981811953909393464456911715387832373381
    
    ---------------------------------------------------------------------------------------
    
    Рассчитайте, пожалуйста, FIR с разумно-близкой АЧХ и меньшим чем у IIR набегом фазы:
    
    Refridgerator
    00.00.0000 00:00
    #25361824
    Не понял вопроса. Это же не произвольная АЧХ, это АЧХ конкретного минимально-фазового фильтра. Понятно, что минимально-фазовее него быть уже не может. А чтобы переделать его в FIR думать вообще не надо — достаточно просто импульсную характеристику замерить.
    
    Вот так она выглядит
    
    А это её спектр через FFT
    
    Тут из полезного разве что фазу обнулить:
    так
    
    Или фазу развернуть, а обнулить амплитуду: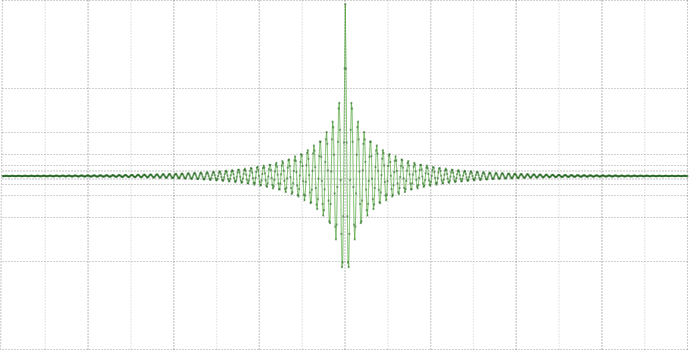
    так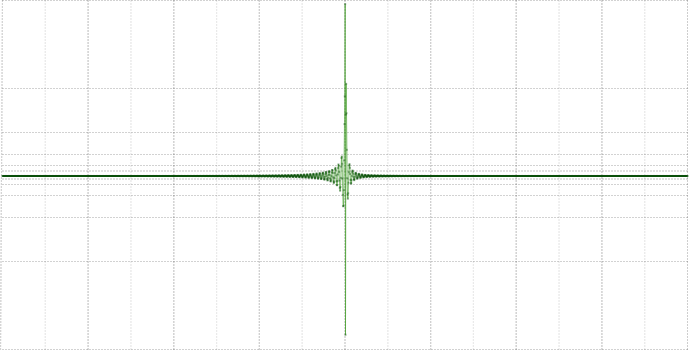
    
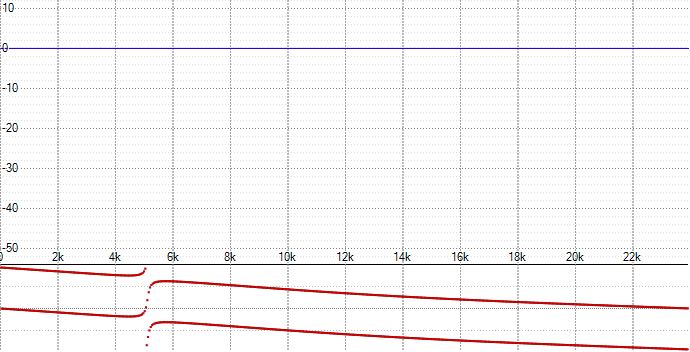
    Произвольная АЧХ потому и произвольная, что её можно нарисовать любую, в зависимости от задачи,
    например
    
    Можно сравнить их импульсные характеристики на одном графике
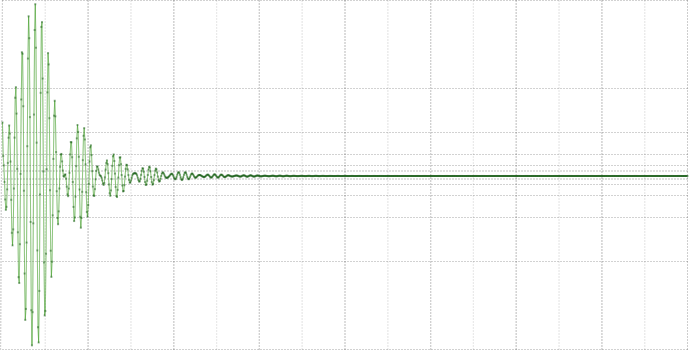
    вот
    
    Второй вариант затухает даже быстрее.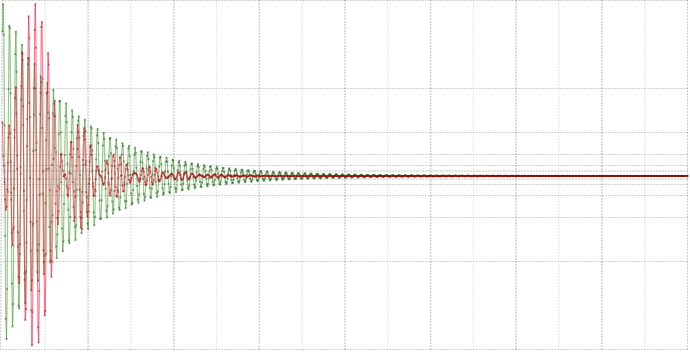
    
    ValeriyS
    00.00.0000 00:00
    #25361892
    Ход ваших мыслей абсолютно правильный, я его только немного продолжил бы:
    
    Минимально-фазовыми могут быть только IIR фильтры.
    
    Если фаза минимальна, то и задержки минимальны.
    
    Поэтому IIR фильтры исключительно популярны в системах управления с обратной связью.
    
    Интересно было бы посмотреть на публикацию, где излагается feedback контроллер, построенный на FIR или FFT.
    
    Что, если я скажу вам, что для произвольной АЧХ, определённой до бесконечно высоких частот, существует только одна минимально-фазовая ФЧХ? По работе, я вычислял эту ФЧХ для любой заданной АЧХ. И эта минимально-фазовая ФЧХ может быть апроксимирована с произольно высокой точностью набором минимально-фазовых SOS IIR фильтров (их количество просто будет расти с ростом требований по точности совпадения АЧХ).
    
    Refridgerator
    00.00.0000 00:00
    #25361916
    Минимально-фазовыми могут быть только IIR фильтры
    Разве мои пример выглядит не достаточно убедительно? IIR имеет бесконечную длину только в теории. На практике она заканчивается как только доходит до шумовой полки или eps.
    
    Интересно было бы посмотреть на публикацию, где излагается feedback контроллер, построенный на FIR или FFT
    Навскидку
    
    Что, если я скажу вам, что для произвольной АЧХ, определённой до бесконечно высоких частот, существует только одна минимально-фазовая ФЧХ?
    А как, по-вашему, мой вариант фильтра получился? Я же не вручную ФЧХ рисовал. ФЧХ посчитался через кепстр. Причём даже без матлаба и прочих маткадов, кодом на си-шарпе.
    
    Arastas
    00.00.0000 00:00
    #25362162
    Я делал системы с FIR в обратной связи для компенсации вибраций. Это позволяло динамически подстраивать параметры при вариации частот вибраций.
    
    konusnyj_flexer
    00.00.0000 00:00
    #25362658
    А насколько далеко частота вибраций была от частот, на которых работала система? Можете что-то сказать по этому поводу https://habr.com/ru/post/724006/#comment_25362626 ?
    
    Arastas
    00.00.0000 00:00
    #25363294
    Вибрации гуляли в диапазоне 50-95 Гц. Задача системы - гасить колебания, то есть стоять в точке.
    
    konusnyj_flexer
    00.00.0000 00:00
    #25363962
    И FIR успешно справился с задачей?
    
    Arastas
    00.00.0000 00:00
    #25364340
    Это была адаптивная система, параметры FIR подстраивались в реальном времени. На прототипе работало хорошо.
    
    ValeriyS
    00.00.0000 00:00
    #25365044
    Для контроллеров нелинейных систем все средства хороши, включая FIR и FFT :)
    
    konusnyj_flexer
    00.00.0000 00:00
    #25362626
    А не подскажите какой максимально резкий спад амплитудной характеристики без существенного изменения фазовой характеристики можно получить с помощью подобных фильтров? С учетом того, чтобы это еще потом смог обсчитывать контроллер (например, какой-нибудь Siemens) в реальном времени. Была задача, где в системе управления в обратной связи был паразитный упругий элемент, резонансная частота которого была довольно близко к полосе пропускания двигателя, что мешало повысить быстродействие системы. Например, если у двигателя была полоса пропускания около 25 Гц, то собственная частота колебаний упругого элемента была около 50Гц. Добавление фильтров с довольно крутым спадом АЧХ, увеличивало задержку в обратной связи, а меньшие порядки фильтров не особо срезали ненужную частоту упругого элемента по причине его близости к полосе пропускания движка
    
    ValeriyS
    00.00.0000 00:00
    #25364804
    Да, ваша задача это практически идеальный пример, когда использование IIR фильтра с нулями/полюсами обратными резонансу на 50 Гц было бы верным решением. Мы работали с системами, где подрбных резонансов в полосе пропускания было 3-5 штук. Чем точнее мы их измеряли, тем точнее была компенсация набором IIR фильтров, тем более высокую полосу пропускания можно было получить для feedback loop.
    
    Если есть резкое изменение амплитудной характеристики, значит ваш plant имеет и такое же резкое изменение фазы в данном месте. Просто надо помнить, чо механические системы это набор резонансных элементов, для которых амплитуда и фаза всегда взаимно связаны. Поэтому когда мы компенсируем амплитуду нашего plant с помощью IIR мы заодно компенсируем его фазу.
    
    Даже классический PID контроллер является частным случаем минимально-фазового IIR фильтра :)
    
    Что касается стандартных контроллеров, то нередко у них есть опция включения резонансных фильтров, реализованных как подмножество IIR фильтров. Полной гибкости конечно нет, произвольные нули/полюса так не погасишь.
    
    Сейчас стали появляться контроллеры, позоляющие реализовать практически любую архитектуру управления. Это делается путём компиляции вашей Simulink модели прямо в код, исполняемый в процессоре контроллера. В этом случа мы можем достроить достаточное количество универсальных IIR фильтров с произвольным набором нулей/полюсов.
  1. konusnyj_flexer
    00.00.0000 00:00
    #25359320
    Согласен, что в цифре можно не париться, если вы имеете в виду, что регулятор, реализуемый внутри контроллера, может иметь любую произвольную функцию. То есть да, не надо подбирать схемы с резисторами, конденсаторами и индуктивностями, чтобы его реализовать. Но насколько я понял из статьи, нули и полюса (которые определяют поведение системы в целом, а не только регулятора) там используются, чтобы выбрать коэффициенты для регулятора, то есть не надо их подбирать вручную или экспериментально. Если я правильно Вас понял, то Вы предлагаете модель системы записать в виде нелинейных уравнений, а уж само регулирование подбирать вручную, экспериментально? Поправьте, если ошибся
    
    Refridgerator
    00.00.0000 00:00
    #25359444
    Нет, я ничего не предлагаю, я просто ответил на вопрос со своей точки зрения. Численное решение дифференциальных уравнений придумали задолго до, и для численного решения линеаризация не требуется. Подбирать параметры экспериментально — не значит вручную их перебирать. Это значит автоматический итеративный процесс с минимизацией ошибки. Или например замерить спектр и численно его инвертировать с последующим сглаживанием.
    
    Нули и полюса не определяют поведение системы в целом. Поведение системы в целом определяют функции, по которым она переходит из одного состояния в другое. Нули и полюса по определению имеют смысл только для рациональных многочленов конечной степени.
    
    konusnyj_flexer
    00.00.0000 00:00
    #25359692
    Ну видимо мы с Вами говорим немного о разных системах. Те, которые мне попадались в рамках ТАУ, были по большей части механические и описывались передаточной функцией (или несколькими) с, как вы и сказали, многочленами в числителе и знаменателе. И именно корни этих многочленов определяли функции (являющиеся решением дифференциальных уравнений), по которым система переходит из одного состояния в другое
  1. belch84
    00.00.0000 00:00
    #25359364
    +1
    Да, можно поступить так. После преобразований уравнения, разрешенные относительно старших производных, будут выглядеть так
    
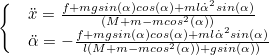
    Введем следующие обозначения
    
    (внешнее воздействие представляется в виде линейной функции от времени),
    
    и перепишем уравнения в виде (следите за руками)
    
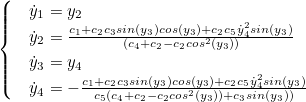
    Теперь можно вручную поизменять параметры
    
    График зависимости угла отклонения alpha от времени
    
    Подвигаем ползунки
    
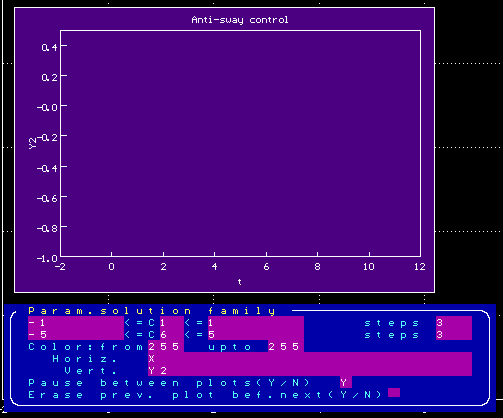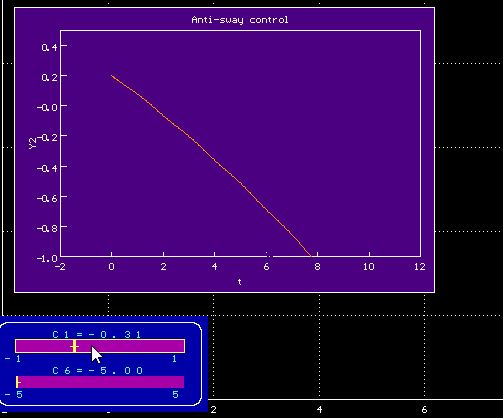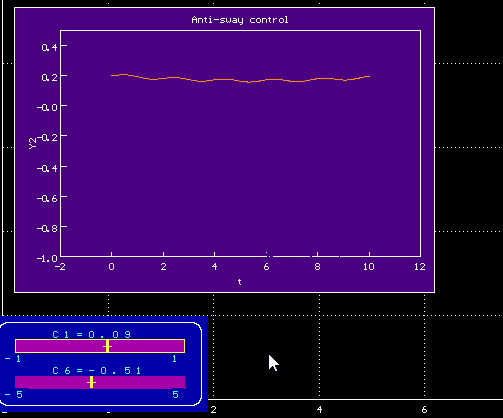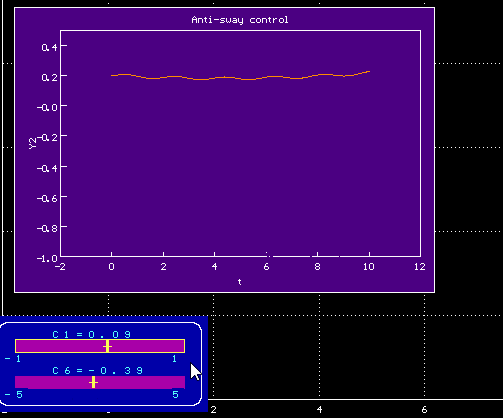
    Изменяя параметры внешнего воздействия, можно добиться. чтобы график для угла не сильно отклонялся от горизонтали, т.е. чтобы колебания были невелики
    
    Все это, конечно, является методом "грубой силы", но зато не требуются довольно сложные рассуждения об управлении. Здесь все просто — справится даже крановщик. Разумеется, я мог где-то ошибиться (например, в преобразовании системы к явно зависящей от старших производных), но принципиально задачу можно решить исключительно численными методами
    
    konusnyj_flexer
    00.00.0000 00:00
    #25359920
    Интересный подход. И спасибо, что так подробно описали, да еще и с видео. Только немного не понял, что это за линия графике. Вы говорите, что ее горизонтальность - это минимальный угол раскачивания, а на оси ординат там переменная Y2, что в Ваших обозначениях вроде как отвечает за скорость тележки
    
    belch84
    00.00.0000 00:00
    #25360066
    Вы правы, перепутал, вот улучшенный вариант
    
    Исправленный график зависимости угла отклонения alpha от времени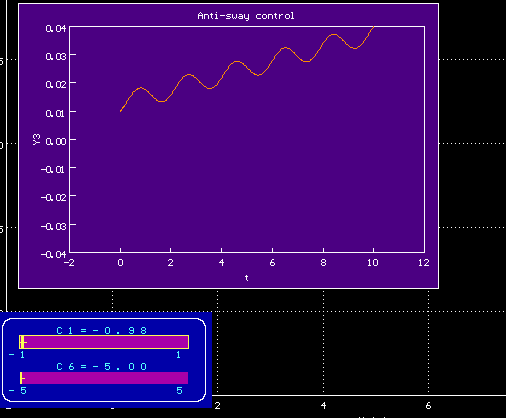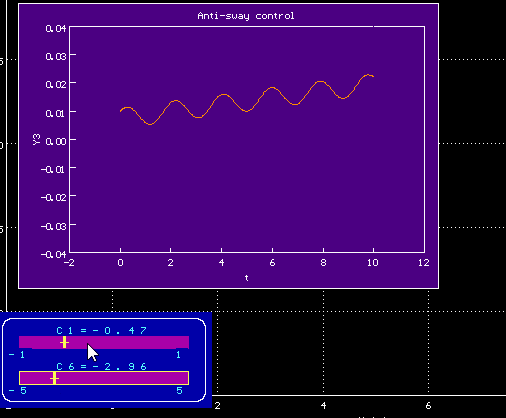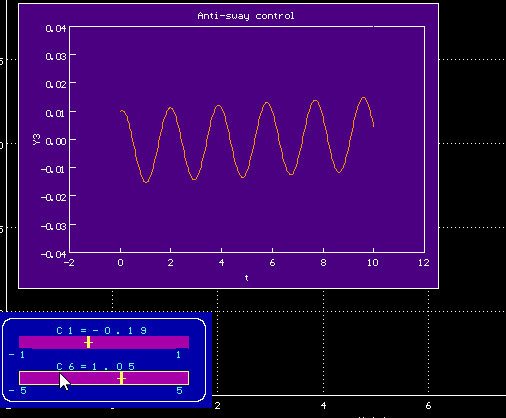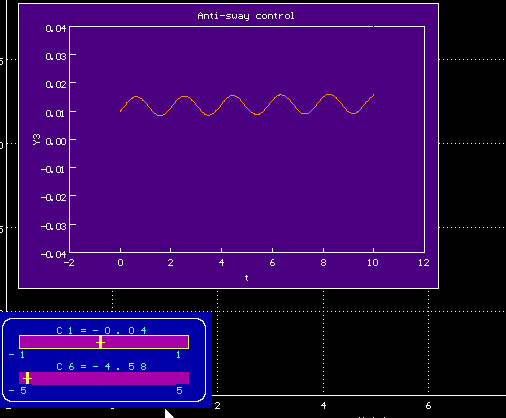
    
    Заметно, что принципиально график изменился не сильно, видимо, угол со скоростью связан как-то примерно пропорционально
    
    LanaVeryatinskaya Автор
    00.00.0000 00:00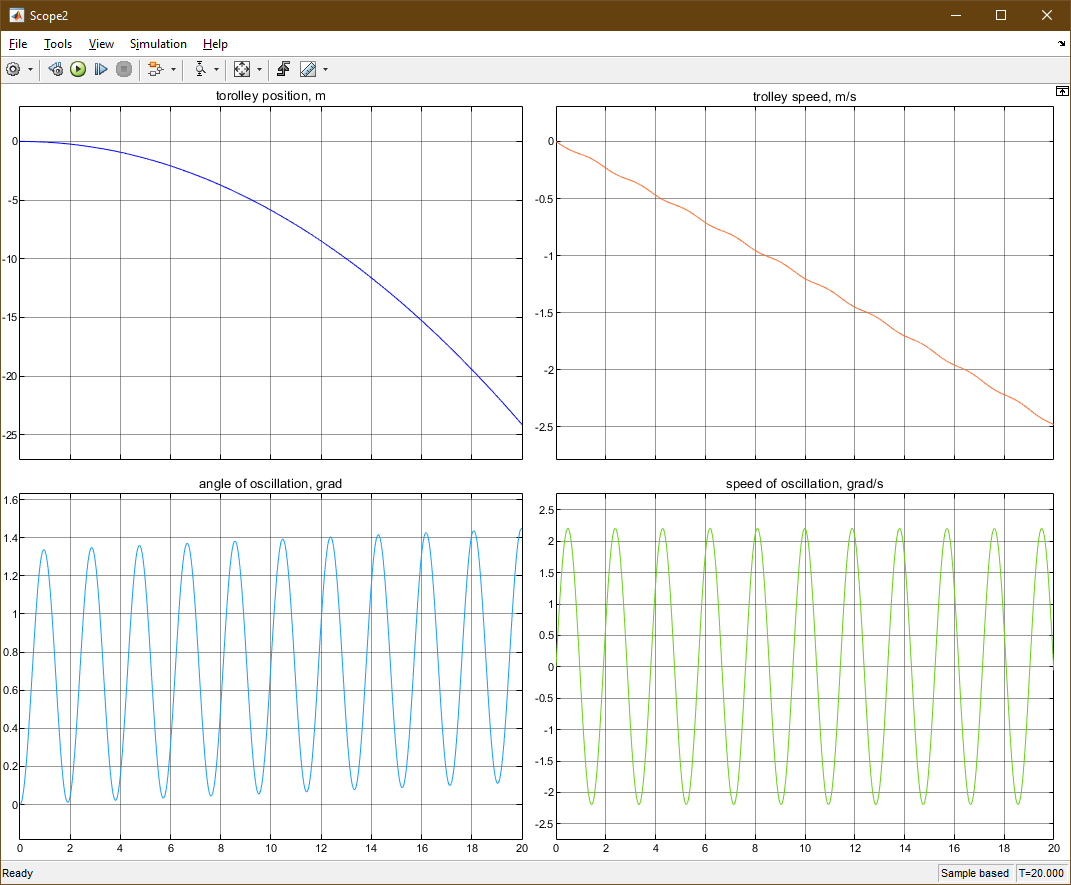
    #25360426
    Попробовала ваш метод, задала воздействие по формуле f=c1*t+c6 с полученными коэффициентами, действительно колебания маятника минимальны. Но тележка едет бесконечно, а нам необходимо, чтобы она пришла в конечную заданную точку за меньшее время.
    Благодарю за ваши комментарии и решения!

belch84
00.00.0000 00:00
#25357814
Система нелинейная и надо это исправить, потому что иначе не выйдет далее перейти к нормальной форме Коши

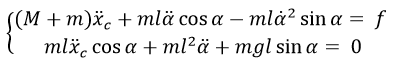
Строго говоря, это не так — вторая производная от alpha входит во второе уравнение линейно, её можно выразить через все остальное, потом подставить выражение в первое уравнение, решить его относительно второй производной от X, потом полученное выражение подставить в выражение для второй производной от alpha. В результате возникнет система двух уравнений второго порядка, разрешенных относительно высших производных. Но выражения там получатся пугающие
1. Arastas
  00.00.0000 00:00
  #25357832
  Это линейная система уравнений относительно вторых производных, которую часто удобнее записать в матричном виде.
  1. belch84
    00.00.0000 00:00
    #25357900
    Не очень понял, как эту систему можно считать линейной, когда там синусы и косинусы от одной из переменных (а также её квадрат). Линейность по вторым производным дает возможность выписать уравнения явно, но сами эти уравнения в матричном виде уже не запишешь
    
    Arastas
    00.00.0000 00:00
    #25358044
    В матричном виде тоже относительно вторых производных. $M(q)\ddot{q} +C(q,\dot{q}) + G(q) =f$ , где q - обобщенная координата.

sys_Arch
00.00.0000 00:00
#25358424
\\\... Постановка задачи: прийти в заданную позицию за наименьшее количество времени, не превышая доступную скорость и без раскачивания груза. Все ограничения взяты из характеристик стенда, для которого производятся расчеты. ...///

(из практики) Постановка задачи (для разработки математического алгоритма решения и вытекающих электро-механических требований к приводным механизмам и кинематической конструкции):

Выполнить захват/перемещение/освобождение/возврат_пустого SingleCargoUnit из позиции LoadPoint в позицию ReleasePoint (аналогично для MultiCargoUnits = = план погрузки)
- за время, менее заданного лимита, без превышения максимального ускорения для Груза;
- с нахождением минимальной полной стоимости Погрузки (Энергия + Расход ресурса агрегатов => будут несколько оптимумов, для разных кобинаций приводных агрегатов и вариантов кинематики);
Что в итоге приводит к набору Траекторий и динамике по траектории, для перемещения Груза. После чего математический аппарат и алгоритм, будут существенно отличаться от предложенного выше, а с учетом "посадки на заданную вычислительную архитектуру" - измениться еще больше и поменяется до неузнаваемоти.когда опора крана, точка места взятия груза, точка места освобождения груза - будут подвижны + ветер + охлаждение/перегрев/изменение темпа работы агрегатов (в частности перегрузка судно-судно в открытом море).

Итого: рекомендую разрабатывать controlAlgorithm, когда на входе заданы для Груза: сплайн Траектории, сплайн(ом) Ориентации, сплайн(ом) Скорости, смещение точки захвата относительно центра масс (опционально).

На выходе алгоритма 2D экономайзер (то что видит Оператор или Робот), KWt*hr vs Money (расход ресурса агрегатов). Задача оператора или Робота управлять "джойстиком / api command", удерживая точку слежения экономайзера в заданной 2D области.
1. KanSergo
  00.00.0000 00:00
  #25358722
  Возможно постановка задачи в статье поставлена не корректно, так как изначально задача здесь стояла: погасить раскачивания создаваемые заданием скорости от оператора либо от внешних воздействий. То что вы предлагаете мы пробовали, работает, когда идёт задача позиционирования. Но здесь цель создать регулятор, который бы обрабатывал задание оператора и текущие значения раскачивания и выдавал задание с минимальным раскачиванием груза.
1. KanSergo
  00.00.0000 00:00
  #25358922
  Касательно вашего алгоритма: как вы рассчитывали траектории движения? Считали потребляемую энергию для всех траекторий и использовали какой-то алгоритм подбора минимального значения? А как в этом расчете учитывали необходимость обеспечить минимальное раскачивание?
  1. sys_Arch
    00.00.0000 00:00
    #25360540
    для абсолютного большинства случаев, принцип расчета оптимальной траектории (картинка выше) - достаточен.
    
    Стационарные положения в начале и на завершении траектории, плюс известные значения cargoMass, cargoVelocity, cargoWindDrag, windVelocityVector - jпозволяют однозначно рассчитать число Джоулей, для перемещения cargo из одной точки в другую по траектории с заданной динамикой.и ориентацией.
    
    Правила безопасности при подъеме / перемещении грузов - требуют наложения ограничений на положение груза в каждой точке траектории. Управляющий (приводами) алгоритм, работает от обратного (на каждом шаге) - берет на вход текущие значения инерционных характеристик груза + будущую позицию и ориентацию груза, далее по классике высчитываем потребную для шага энергию, под заданную "кинематическую матрицу".
    
    Все виды компенсаций от раскачивания, порывов ветра, смещения груза - сводятся к изменению шага "интегрирования", то есть темпу вычислений (до предела возможностей приводов и прочности конструкции).
    
    konusnyj_flexer
    00.00.0000 00:00
    #25362736
    Все равно не понял каким образом будет строиться траектория перемещения груза. Зеленую и красную траектории на Вашем рисунке понимаю, это как бы наше идеальное задание. А вот сплайны не понимаю каким образом будут строиться, чтобы в конце перемещения груз не раскачивался. Вы пишите (насколько я понял), что алгоритм берет текущие характеристики груза и тележки, потом что-то высчитывается и вот мы движемся. Но не понятно, что происходит в момент, когда "что-то высчитывается"
    
    sys_Arch
    00.00.0000 00:00
    #25365306
    (Траектории) Синий (подъем) -> ::Желтый (перемещение) -> Фиолетовый (опускание) участки траекторий, представляют собой кубические сплайны, 3-ий порядок сплайна достаточен для всех видов тросовых подъемных систем. Большие порядки, спиральные формы применяются для жесткой кинематики и систем с электрической рекуперацией, где более важна гладкость второй и более производных (каждый разгон и торможение Груза = затраты энергии, F(t)=m*a(t) ).
    
    Вращайте плоскости (показаны специально, угол вращения есть параметр; также как угол наклона сплошного Зеленого отрезка) на которых построены Синии и Фиолетовый сплайны, задавайте предельное отклонение Желтого сплайна от Зеленого отрезка => :Желтый сплайн будет иметь единственную наивыгоднейшую форму.
    
    Синий сплайн имеет "экспоненциальную" форму (перед началом подъема, уже точно известо в какую сторону вести груз), Задавая/измеряя профиль скорости подъема и подъемную силу (энкодер и сила тока тягового двигателя, как минимальный вариант) -> получите массу Груза. Ваша цель - разогнать Груз в заданную сторону, чтобы Каретка на Стреле двигалась линейно (паралелельно и в плоскости сплошной Зеленой линии), тогда Груз отклониться и пойдет по Желтому сплайну (инерционная оттяжка).
    
    Фиолетовый сплайн, имеет форму "гашения инерции" (контрольная точка обращение в ноль горизонтальной Скорости и Ускорения). При дальнейшем опускании, существует единственный профиль темпа перемещения Каретки и Стрелы, когда горизонтальный колебания Груза переходят во вращательные колебания относительно центра Масс Груза (де факто в прецессию вокруг Z оси). Нужно успеть опустить Груз на опору за время пока накопленная Инерция Груза переходит "из одного состояния в другое". При необходимости зависания Груза, профиль темпа перемщения Каретки и Стрелы имеет несколько вариантов для сохранения колебания/прецесии вокруг центра масс груза (собственные частоты колебаний систкмы Груз/Захват/Подвес), то есть минимальные отклонения в горизонтаьной плоскости.
    
    (Алгоритм и математические преобразования) - пишите в личку.

artyrvinogradov42
00.00.0000 00:00
#25358426
В матричном виде проще записать такие уравнения

Tarakanator
00.00.0000 00:00
#25358526
+1
Тут конечно только результат демонстрируют, но он куда круче будет
https://pikabu.ru/story/pervoe_v_mire_video_s_56_yelementami_upravleniya_perekhodom_dlya_troynogo_perevernutogo_mayatnika_10060378#comments
1. KanSergo
  00.00.0000 00:00
  #25358734
  Все с чего то начинают. )
1. konusnyj_flexer
  00.00.0000 00:00
  #25362686
  В Вашем примере думаю несколько другая задача, где основная цель это удержание маятника в равновесии. А в статье скорее основная цель придти в заданную точку или набрать нужную скорость без колебаний маятника. То есть больше похожа на что-то такое https://www.youtube.com/watch?v=UqyZW6F7eWY
  1. Tarakanator
    00.00.0000 00:00
    #25362806
    И там и там колебания. Задача несколько другая конечно, но крутость моего варианта перевешивает разницу имхо
    
    LanaVeryatinskaya Автор
    00.00.0000 00:00
    #25363964
    Наша модель тоже может работать быстрее, но углы раскачивания больше и высокая скорость, у движка может не хватить мощности реализовать ее. Также на том видео тележку двигает ременная передача, а у нас колеса, которые могут проскальзывать при больших ускорениях https://disk.yandex.ru/i/MLiPlK0T3faFaQ
    
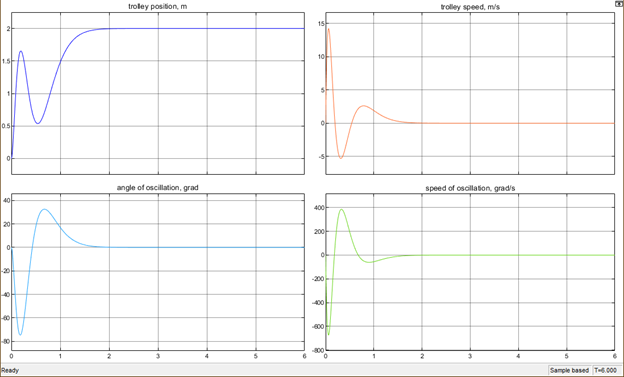
    Тележка крана имеет ограничения, которые мы учитываем, поэтому такие результаты. https://disk.yandex.ru/i/wmxeO8Z5RdoG2g

Система противораскачивания груза (Anti-Sway Control) +31

Дифференциальные уравнения

Пространство состояний

Модель тележки с грузом с управлением по скорости

Дифференциальные уравнения

Матрицы пространства состояния

Выбор регулятора

Синтез регулятора

Алгоритм расчета параметров модального регулятора

Выбор корней

Подбор корней для решения задачи движения по положению

Выбор корней для решения задачи движения с заданной скоростью и в заданную позицию

Светлана Верятинская

Комментарии (61)

LanaVeryatinskaya Автор

LanaVeryatinskaya Автор

LanaVeryatinskaya Автор

LanaVeryatinskaya Автор

LanaVeryatinskaya Автор

LanaVeryatinskaya Автор