Приветствую, меня зовут Алёна. Недавно на математический основах информатики в университете мы проходили задачу сетевого планирования, с помощью которой можно смоделировать процесс производства изделий. Мне была интересна данная тема и я решила поделиться с вами, как решить задачу сетевого планирования с использованием языка Python.
Определения
Сетевая модель — сетевой график, элементами которого (вершинами / дугами / и тем и другим) поставлены в соответствие некоторые величины, называемые весами.
С помощью сетевой модели будем моделировать процесс производства некоторого нового изделия. Вершины будут соответствовать моментам начала или окончания выполнения работ, дуги будут соответствовать условиям взаимозависимости выполняемых работ, а веса на дугах будут соответствовать ожидаемым длительностям выполнения работ.
Суть задачи: требуется определить минимально возможное время, за которое можно выполнить все работы.
Терминология
Введём обозначения:
i- номер работыt(i)- длительность выполнения работыiK(i)— множество работ, предшествующих работе с номеромi
Для решения задачи пользуются специальной схемой расчета временных характеристик, позволяющей не только дать ответ на поставленный вопрос, но и найти дополнительные характеристики, позволяющие более эффективно управлять процессом изготовления нового изделия.
К таким характеристикам относятся:
t(rn, i)- время самого раннего начала выполнения работы с номеромit(rk, i)- время самого раннего окончания выполнения работы с номеромit(pn, i)- время самого позднего начала выполнения работы с номеромit(pk, i)- время самого позднего окончания выполнения работы с номеромir(i)- резерв времени работы с номеромi, т.е. время, на которое не в ущерб времени общего окончания выполнения всех работ, можно задерживать выполнение работы с номеромiT(k)- время выполнения всех работ изделия.T(k)- длина критического пути, а критическим путём называют путь, соединяющий некоторую начальную работу - не имеющую предшествующих работ, и некоторую конечную работу - не имеющую последующих, т.е. от неё зависящих работ, суммарное время выполнения всех работ которого максимально.
Формулы
Для расчета временных характеристик будем пользоваться следующими формулами:
t(rn,i) = 0, если K(i) - пустое множество.
t(rk,i) = t(rn,i) + t(i) t(rn,i)= max t(rk,j), где максимум берется по всем работам j из множества K(i).
t(pk,i) = t(rk,i), если работа i не имеет последующих.
t(pn,i) = t(pk,i) - t(i) t(pk,i) = min t(pn,j), где минимум берется по тем работам j, которые принадлежат множеству K(i), т.е. по тем работам, от которых зависит работа с номером i.
r(i) = t(pn,i) - t(rn,i) = t(pk,i) - t(rk,i). Работы критического пути — это те работы, резервы времени которых нулевые (r(i) = 0).
Условия
Граф должен быть без петель и контуров, т.е. антирефлексивным бинарным отношением.
Вы должны знать конечную работу. Значение времени критического пути смотрится у конечной работы в столбце t(pk, i).
Пример задачи
Исходные данные:
Итоговая таблица с вычисленными значениями примет вид:
Конечная работа с номером 12. Смотрим у неё значение столбца t(pk, i). Время, за которое гарантированно можно выполнить все работы = 22.
Пишем алгоритм на Python
Создание моделей для хранения входных данных, считывание данных, хранение исходных данных.
Начнём с создания модели, которая будет поступать на вход и второй модели, которая будет заполнять нашу таблицу для планирования. Для удобства использую namedtuple (почитать про него можно тут: https://habr.com/ru/articles/438162/):
from collections import namedtuple
input_model = namedtuple("input_model", ["time", "set_k"])
row = namedtuple("row", ["i", "time", "set_k", "rn", "rk", "pn", "pk", "r"])Считаем количество работ, которое нужно будет обработать:
n = int(input("Введите количество работ="))
Создаём словарь, в который будем помещать исходные данные, на которых будет строиться наше решение. Для удобства я использую типизацию, с которой в дальнейшем мне удобнее писать код:
models: dict[int, input_model] = dict()
Считываем данные (ничего нового). Сначала считываем время, которое тратит работа с номером i, потом вводим множество K(i) - множество работ, которые предшествует введённой работе с номером i (работа c номером i зависит от множества K(i)):
for i in range(1, n + 1):
time = int(input(f"Введите время t({i})="))
raw_k = input(f"Введите через пробел множество K({i})=")
set_k = set(map(lambda data: int(data), raw_k.split()))
models[i] = input_model(time=time, set_k=set_k)
Создаём таблицу, в которой будут храниться итоговые данные:
table: dict[int, row] = dict()
Считаем значения t(rn, i), t(rk, i).
По введённым данным начинаем решать задачу сетевого планирования:
Если у работы нет предшествующих работ (длина множества K(i) = 0), значит это первая работа, с которой начнёт работать наш завод.
Иначе - определяем максимальное значение раннего окончания зависимых работ.
Обновляем таблицу.
for number, model in models.items():
time = model.time
set_k = model.set_k
if len(set_k) == 0:
rn = 1
else:
rn = max([table[s].rk for s in set_k]) + 1
rk = rn + model.time - 1
table[number] = row(i=number, time=time, set_k=set_k, rn=rn, rk=rk, pn=None, pk=None, r=None)
При подсчётах можно увидеть прибавление или убавление единицы. Это дополнительный такт времени, в принципе решать задачу можно без него.
Считаем t(pk, i), t(pn, i), r.
Продолжаем решать задачу сетевого планирования. Проходимся с конца таблицы (последней работы) для подсчётов:
Ищем все посещённые работы с помощью функции
search_next_numbers.t(pk, i) - времени самого позднего окончания выполнения работы, считается как минимальное значение выполненных работ.
t(pn, i) - времени самого позднего начала выполнения работы, считается как t(pk, i) минус время выполнения работы.
r - резерв времени, считается как t(pn, i) минус t(rn, i).
В конце можно увидеть assert: проверка на корректность решения задачи (резерв времени должен быть всегда равен времени позднего окончания - времени раннего окончания). Эта строка необязательна, так как использование assert’ов в коде можно отключить и лучше использовать вызовы ошибок с помощью raise Error :).
Обновляем данные в таблице.
for number, model in list(models.items())[::-1]:
visited = search_next_numbers(number)
current_row = table[number]
if visited:
k = min(visited, key=lambda num: table[num].pn if table[num].pn is not None else 10000000000)
pk = table[k].pn - 1
else:
pk = current_row.rk
pn = pk - current_row.time + 1
r = pn - current_row.rn
assert r == pk - current_row.rk and r >= 0, print(f"{current_row}, r={r}, {pk - current_row.rk}")
table[number] = table[number]._replace(pk=pk, pn=pn, r=r)
Выводим итоговую таблицу.
Для вывода таблицы я использовала библиотеку prettytable. Написала функцию, которая по созданному словарику с табличными данными, будет выводить таблицу:
from prettytable import PrettyTable
def print_table(data: dict[int, row]):
pretty_table = PrettyTable()
pretty_table.field_names = ["i", "t(i)", "K(i)", "t(rn, i)", "t(rk, i)", "t(pn, i)", "t(pk, i)", "r(i)"]
for line in data.values():
pretty_set = line.set_k if len(line.set_k) > 0 else "{}"
pretty_table.add_row([line.i, line.time, pretty_set, line.rn, line.rk, line.pn, line.pk, line.r])
print(pretty_table)
print_table(table)
Заключение
Задачи сетевого планирования могут быть использованы в различных сферах деятельности, подразумевающих организацию процессов и контроль за временем выполнения работ. Например, в строительстве они применяются для планирования и управления проектами, определения зависимостей между работами и трудозатрат, а также для контроля за выполнением сроков. В промышленности задачи сетевого планирования используются для оптимизации производственных процессов и расчета затрат времени и ресурсов на производство изделий. В общем, задачи сетевого планирования могут быть полезны для управления любыми проектами, где время является критическим фактором успеха.
С полным алгоритмом решения задачи сетевого планирования можно ознакомиться по ссылке.
Спасибо за просмотр! Делитесь в комментарии своими мыслями по поводу алгоритма и самой задачи сетевого планирования. До встречи в новых статьях.
Комментарии (5)

molnij
02.06.2023 09:02Хорошо оформленная статья, но к решению много-много вопросов.
Суть задачи: требуется определить минимально возможное время, за которое можно выполнить все работы.
А где в выводе посмотреть это самое минимально возможное время? На гитхабе вы пишете, что
Значение последней строки столбца t(rk, i) будет длиной критического пути (время выполнения всех работ для изготовления изделий).
Но это совершенно точно неправильно. Можете ввести две задачи. У первой длительность 1000 единиц, у второй 10. Предшественников нет ни у одной. Последнее значение будет 10. Правильное — 1000.

alenapoliakova Автор
02.06.2023 09:02+1Спасибо за комментарий. Дополнила немного статью для лучшего понимания, основные моменты, которые добавила:
Граф должен быть полным (каждая вершина соединена ребром).
Вы должны знать конечную работу. Значение времени критического пути смотрится у конечной работы в столбце t(pk, i).
Также в статье написано:
Работы критического пути — это те работы, резервы времени которых нулевые (r(i) = 0).
Отвечаю на вопросы:
А где в выводе посмотреть это самое минимально возможное время?
Как раз для этого строится таблица, по которой можно проследить все подсчёты по формулам из алгоритма, можно проверить. Вы должны знать конечную работу, чтобы посмотреть в таблице время критического пути (по столбцу t(pk, i)).
Можете ввести две задачи. У первой длительность 1000 единиц, у второй 10. Предшественников нет ни у одной. Последнее значение будет 10. Правильное — 1000.
В задаче, что вы предложили граф неполный. Есть две работы (1000 и 10 единиц), которые между собой никак не связаны. Если построить таблицу по таким входным данным получится:
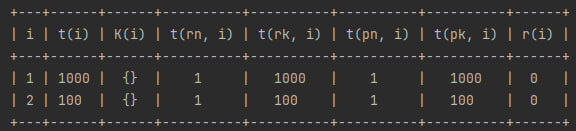
Резервы времени, что у первой работы, что у второй — равны нулю, значит это работы критического пути. Работы не связаны между собой, поэтому в ответе будет 1000 и 100, для первой и второй работы соответственно.
Если я не до конца ответила на вопросы, либо нужны ещё какие-то уточнения, то готова продолжить беседу :).

molnij
02.06.2023 09:02Давайте продолжим, если не возражаете, я по шагам буду продолжать )
Требование полноты графа, это вы конечно перестарались. В этом контексте бы и слабой связности навскидку хватило (кстати ваш алгоритм полноты не переживёт, можете проверить).
Но тогда еще нужно не забыть об ацикличности, а то возникнут проблемы

alenapoliakova Автор
02.06.2023 09:02Граф должен быть без петель и контуров, т.е. антирефлексивным бинарным отношением



Emelyan1
Очень познавательно, спасибо!=)