Данная статья состоит из двух частей:
Часть 1. Мой опыт применения периодической функции активации в нейронных сетях
Часть 2. Перевод некоторых, интересных выжимок из статьи.
Часть 1. Мой опыт применения периодической функции активации в нейронных сетях
Мотивация
Пока крутые ребята создают GigaChat, вернемся к базе.
Изучая нейронные сети, все глубже сталкиваешься с тем, что не ко всем задачам применимы полносвязные глубокие нейронные сети с классическими слоями Linear и слоями активации Relu, Sigmoid, Than и их вариации. Почему не используют остальные функции в качестве активации, например, периодические?
Периодические функции это естественный процесс.
В целом, периодические функции являются одной из самых основных функций, важных для человеческого общества и естествознания: суточные и годовые циклы в мире диктуются периодическими движениями солнечной системы.
Человеческому организму присущи биологические часы, которые носят периодический характер, количество пассажиров в метро меняется ежедневно, а фондовый рынок, курс биткоина это все в своем роде периодические последовательности.
Мировая экономика также следует сложным и накладывающимся друг на друга циклам разных периодов, интересный видеоролик на эту тему есть у Ray Dalio.


Во многих научных сценариях мы хотим смоделировать периодическую систему, чтобы иметь возможность предсказать будущую эволюцию, основываясь на текущих и прошлых наблюдениях. В то время как глубокие нейронные сети являются отличными инструментами для апроксимации. Можно сказать с натяжкой, что они "интерполируют" между существующими данными. Поэтому их реализация плохо подходит для экстраполяции, то есть они не могут обобщить зависимость, особенно периодическую, на известном распределении данных и применить те же правила, патерны в тех местах, где нет обучающих данных.
Если мы заранее знаем, что задача является периодической, мы можем легко решить ее с помощью пребразования Фурье. Однако во многих ситуациях мы априори не знаем, является ли проблема линейно угловой (Relu), периодической или содержит периодический компонент. В таких случаях важно иметь универсальную модель, которая была бы достаточно гибкой для моделирования как периодических, так и непериодических функций.
Расмотрим теоретическую часть, на простых функциях
Применение стандартных подходов
Сгенерируем тренировочные и валидационные данные тривальных функций
y=x, y=sin(x), y=tahn(x), y=x^2
Диапазон train data x=[-20;-4] and [4:20]
Пробел (отсутствие данных) в train data x [-4;4] поможет иследовать способность сети к интерполяции
Диапазон valid data x=[-60;60] валидационная data взята так чтоб посмотреть как себя поведет нейронная сеть на тех диапазонах, где обучающих данных в принципе нет, с помощью этого иследуем эксторпаляцию.
Code gen data:
import torch
import matplotlib.pyplot as plt
import matplotlib
class Gen_data:
def __init__ (self, func, ydown_scale, yup_scale ):
# Data for train
x_train = torch.rand(700)
x_train = x_train * 40.0 - 20.0
self.x_train = x_train[ (x_train <= -4) | (x_train >= 4) ]
self.y_train = func(self.x_train)
# Validate data
self.x_val = torch.linspace(-60, 60, 600)
self.y_val = func(self.x_val)
# For correct view plottig data
self.ydown_scale = ydown_scale
self.yup_scale = yup_scale
def get_train_unsqueeze(self):
return torch.unsqueeze(self.x_train, 1), torch.unsqueeze(self.y_train, 1)
def get_val_unsqueeze(self):
return torch.unsqueeze(self.x_val, 1), torch.unsqueeze(self.y_val, 1)
def plot_initdata(data):
# generate data
x_train = data.x_train
y_train = data.y_train
x_val = data.x_val
y_val = data.y_val
# Plot data
plt.scatter(x_train.numpy(), y_train.numpy(), s=20, color = "purple", label='Train data')
plt.plot(x_val,y_val, 'b-', label='Valid data')
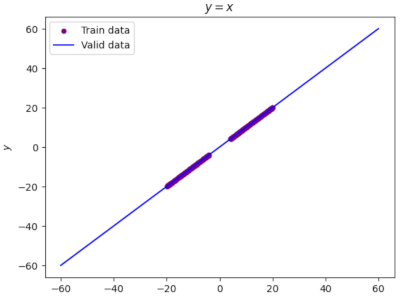
plt.title('$y = x$');
plt.legend(loc='upper left')
plt.xlabel('$x$')
plt.ylabel('$y$')
Сами графики:
code y=x
# Define function
line_func=torch.clone
line_data=Gen_data(line_func, -65,65)
plot_initdata(line_data)
график y=x
code y=sin(x)
matplotlib.rcParams['figure.figsize'] = (30.0, 5.0)
sin_data = Gen_data(torch.sin, -4,4)
plot_initdata(sin_data)
график y=sin(x)

code y=tahn(x)
matplotlib.rcParams['figure.figsize'] = (20.0, 5.0)
tanh_data = Gen_data(torch.tanh, -2,2)
plot_initdata(tanh_data)
график y=tahn(x)

code y=x**2
matplotlib.rcParams['figure.figsize'] = (20.0, 10.0)
# Define function
def parabola(x_input):
return torch.pow(x_input, 2)
parb_data = Gen_data(parabola,-20,400)
plot_initdata(parb_data)
график y=(x)**2
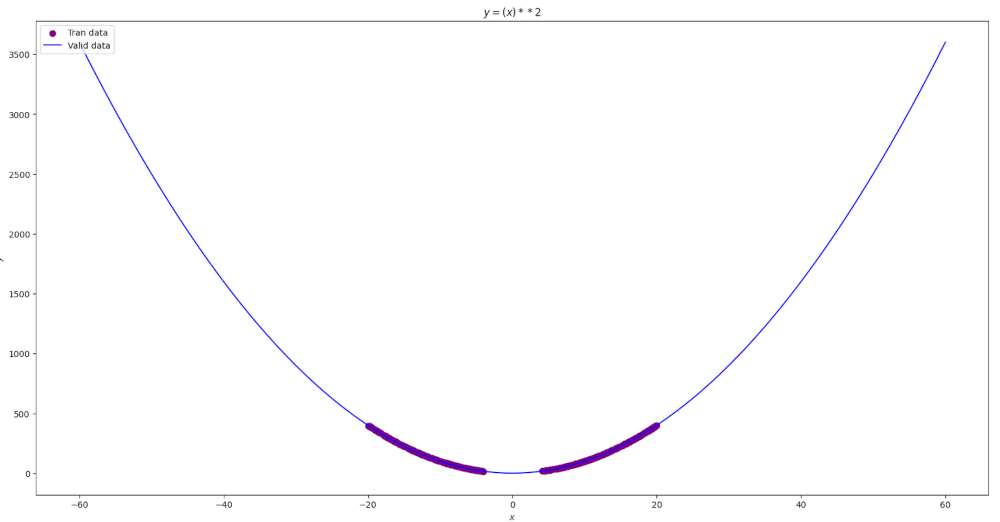
Создадим нейронную сеть
Создадим однослойную полносвязную нейронную сеть с 1 скрытым слоем из 512 нейронов и активационным слоем Relu
code pytorch Net
import torch.nn as nn
import torch
class Net(torch.nn.Module):
def __init__(self, n_hidden_neurons):
super().__init__()
# YOUR CODE HERE
self.fc1 = nn.Linear(1, n_hidden_neurons)
self.act_relu = nn.ReLU()
self.fc2 = nn.Linear(n_hidden_neurons, 1)
pass
def forward(self, x):
x = self.fc1(x)
x = self.act_relu(x)
x = self.fc2(x)
return x
def loss(pred, target):
squares = (pred - target)**2
return squares.mean()

Будем тренировать данную сеть на наших заготовленных данных:
Результат на функции y=x
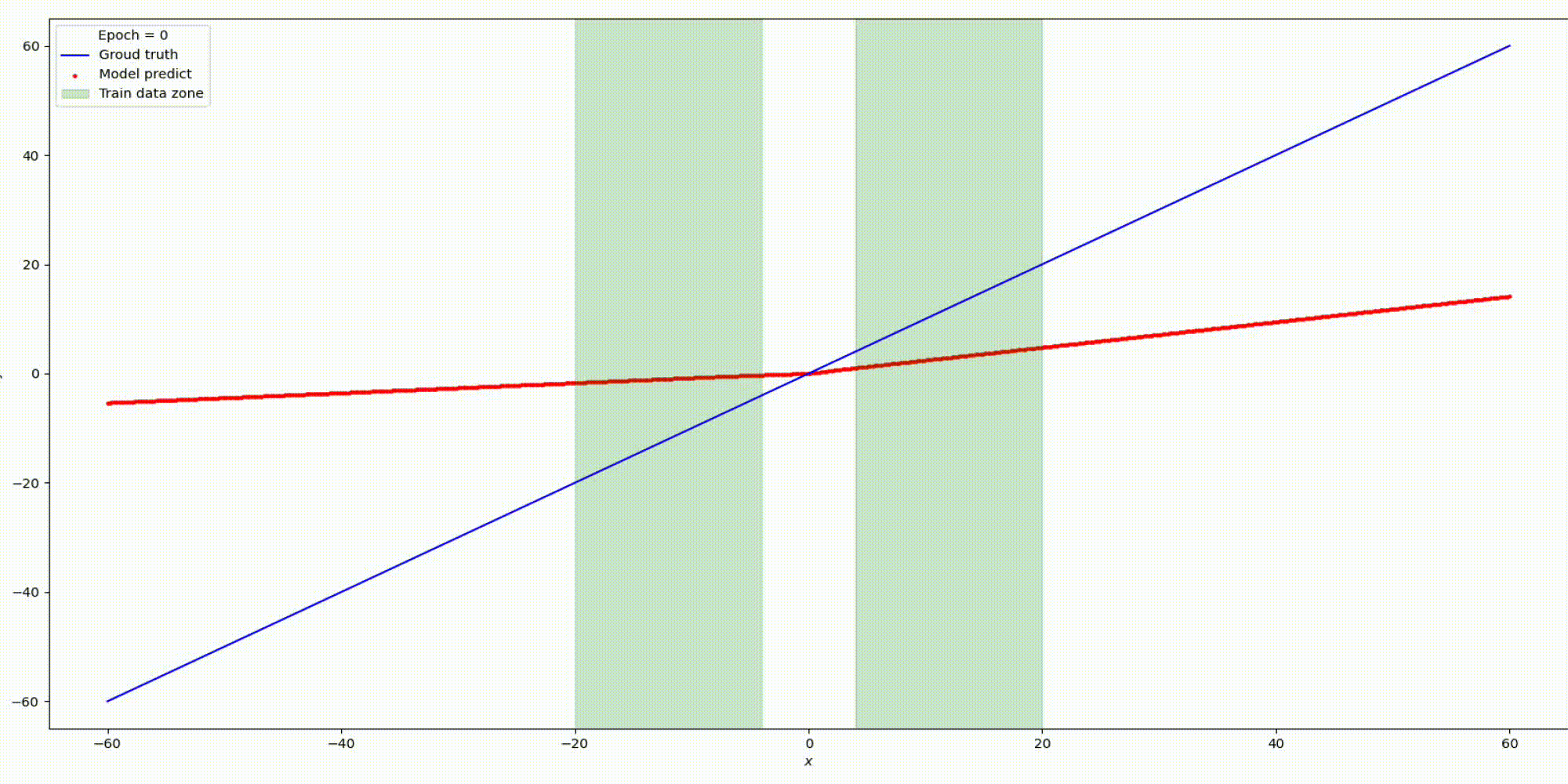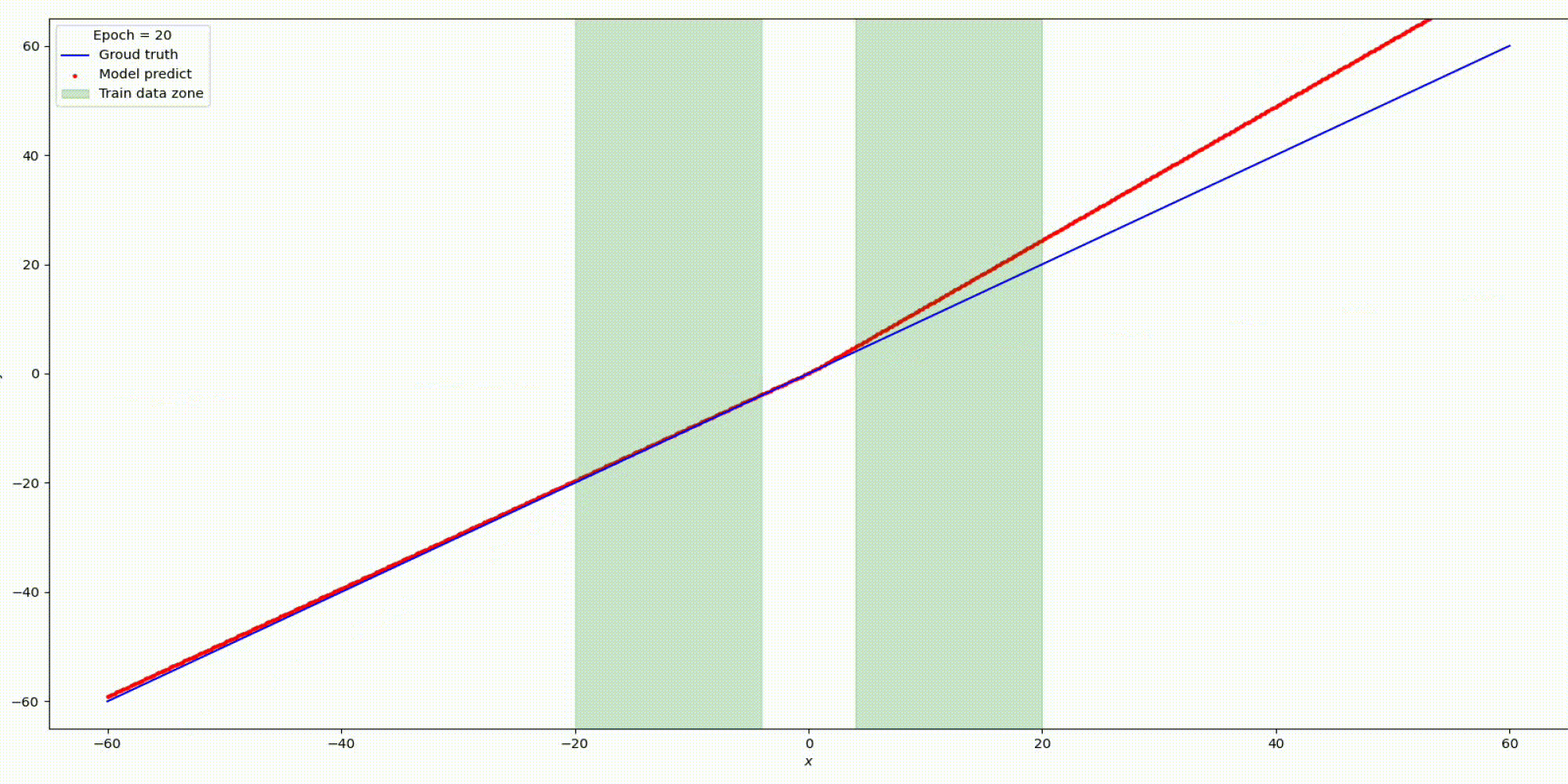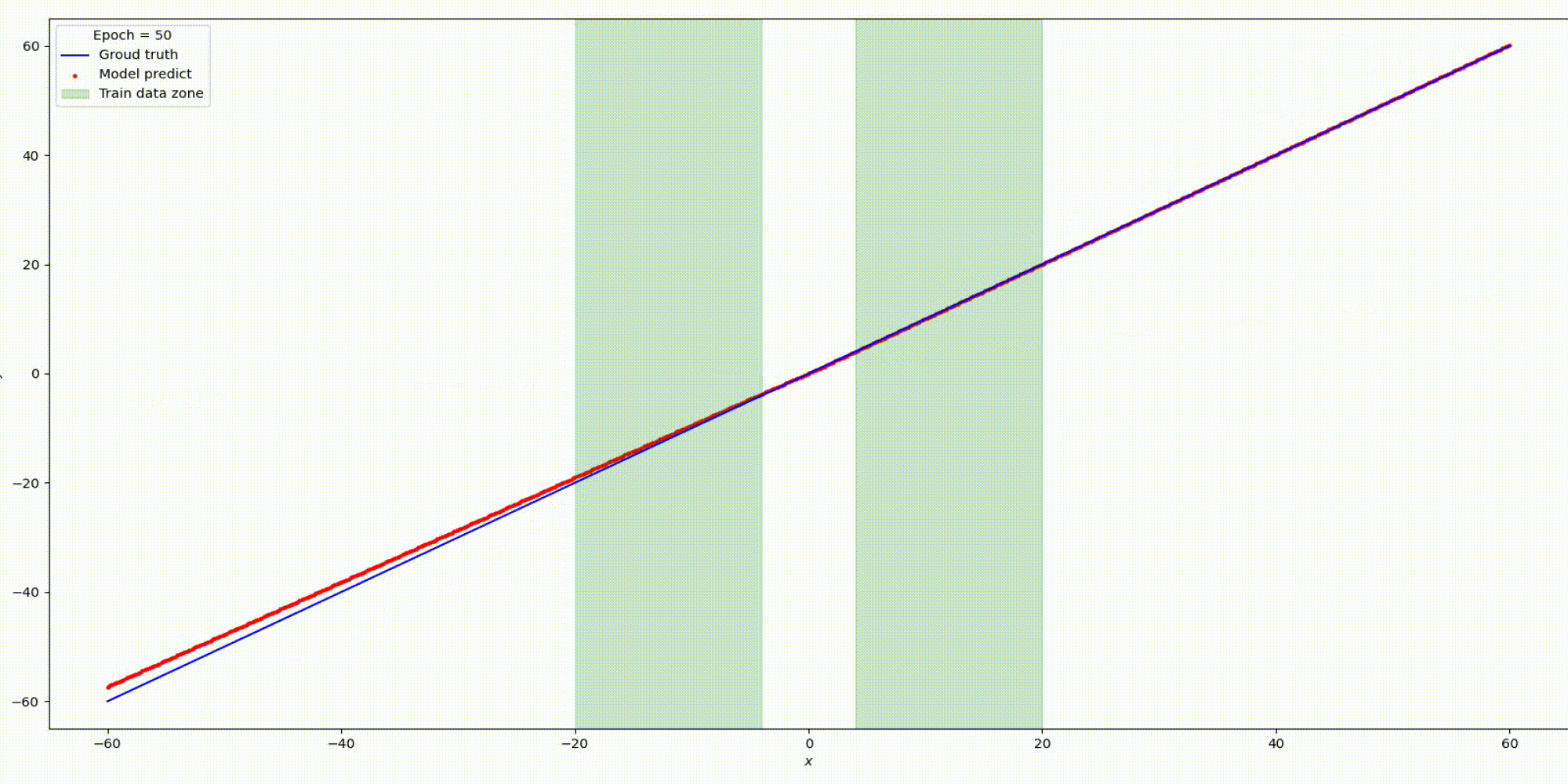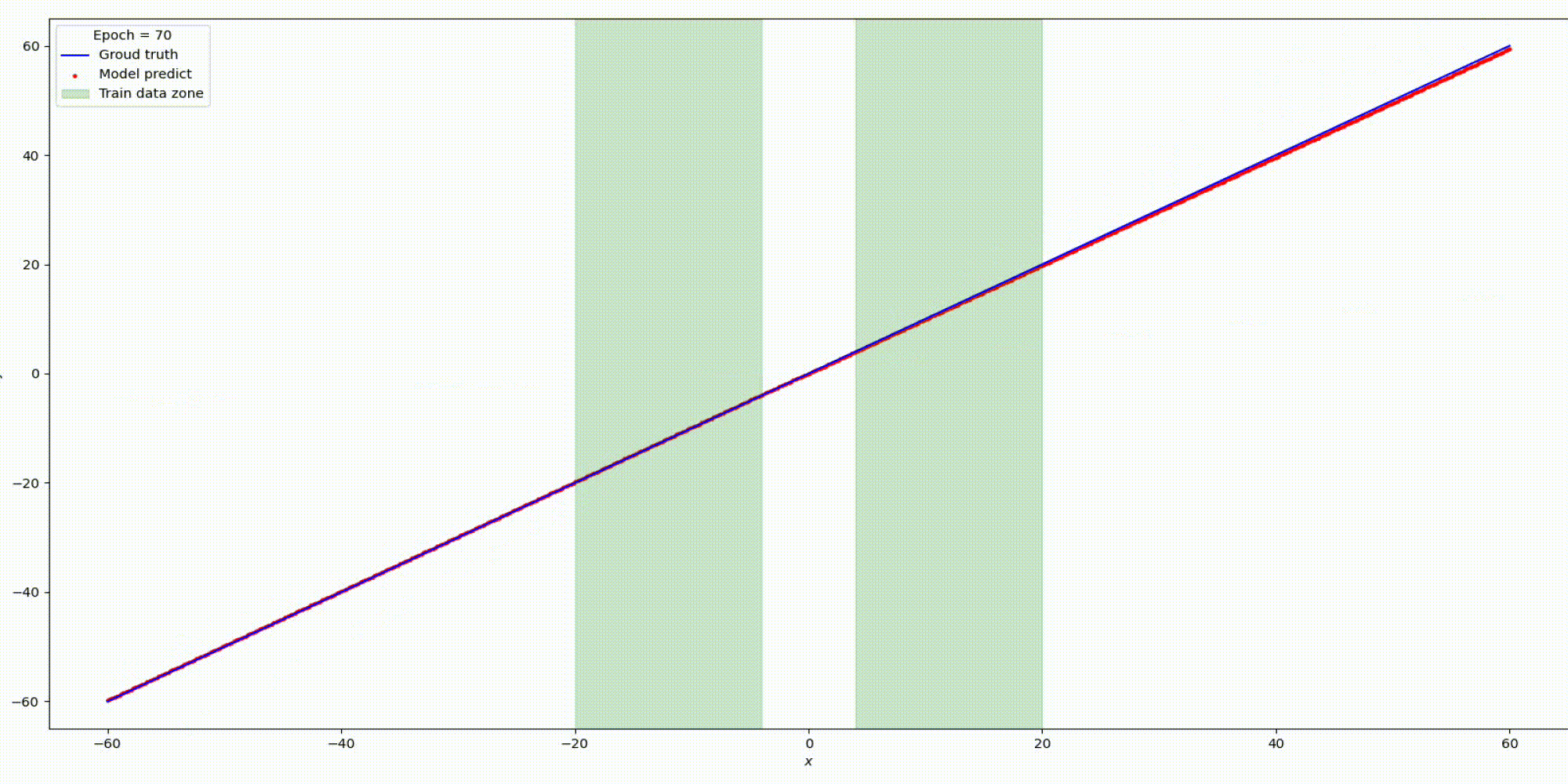

Результат на функции y=sin(x)


Результат на функции y=tanh(x)
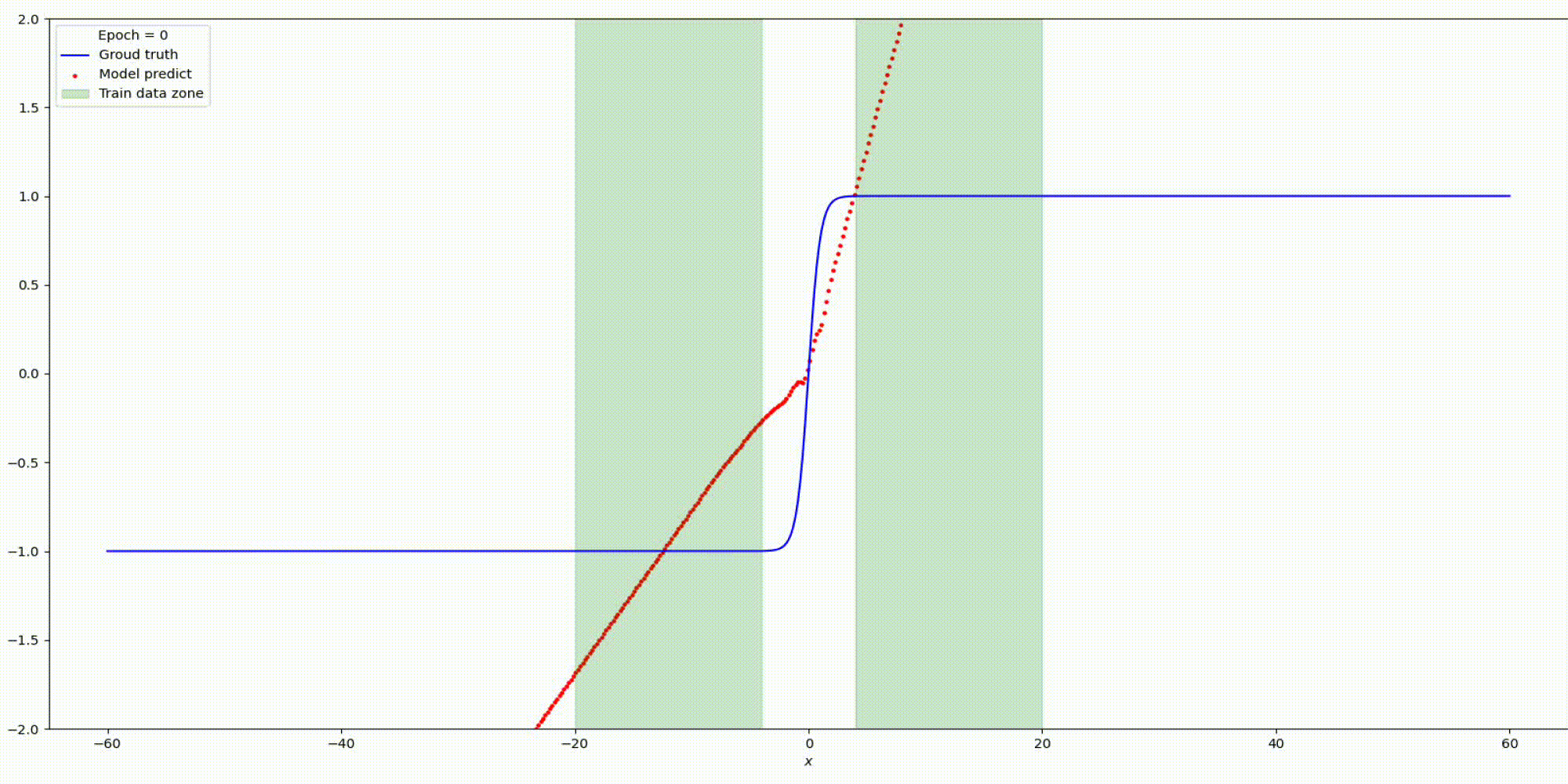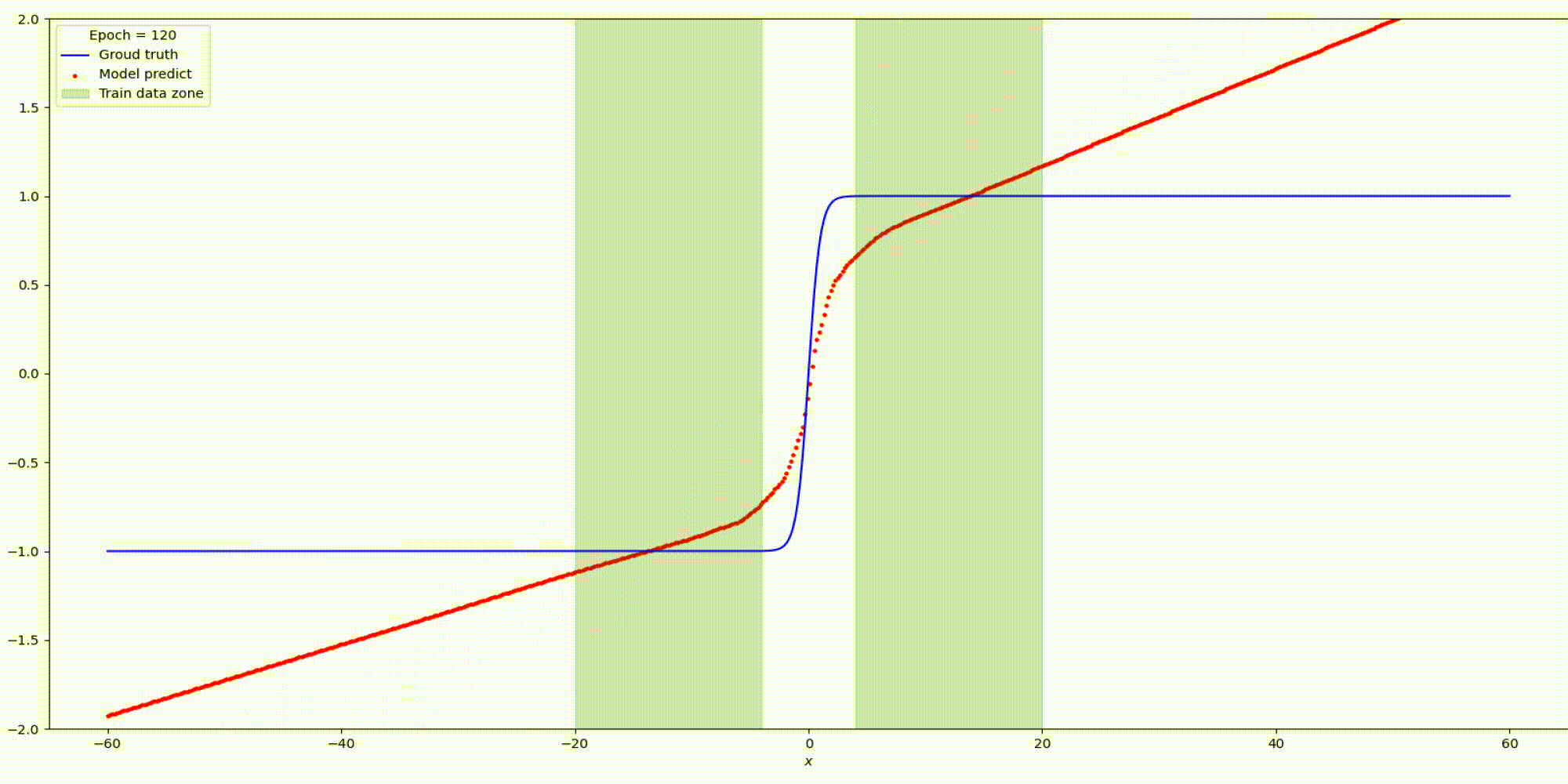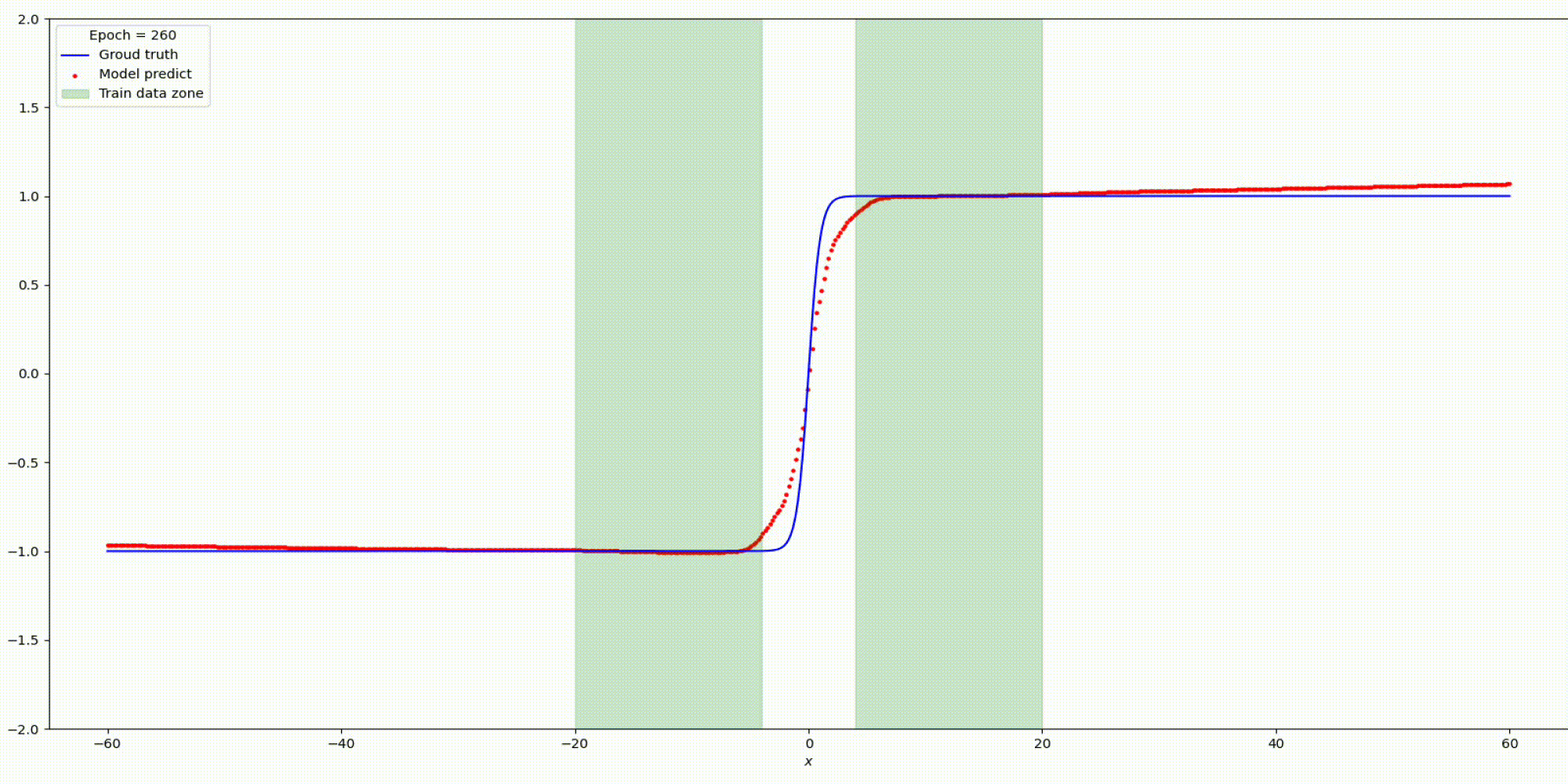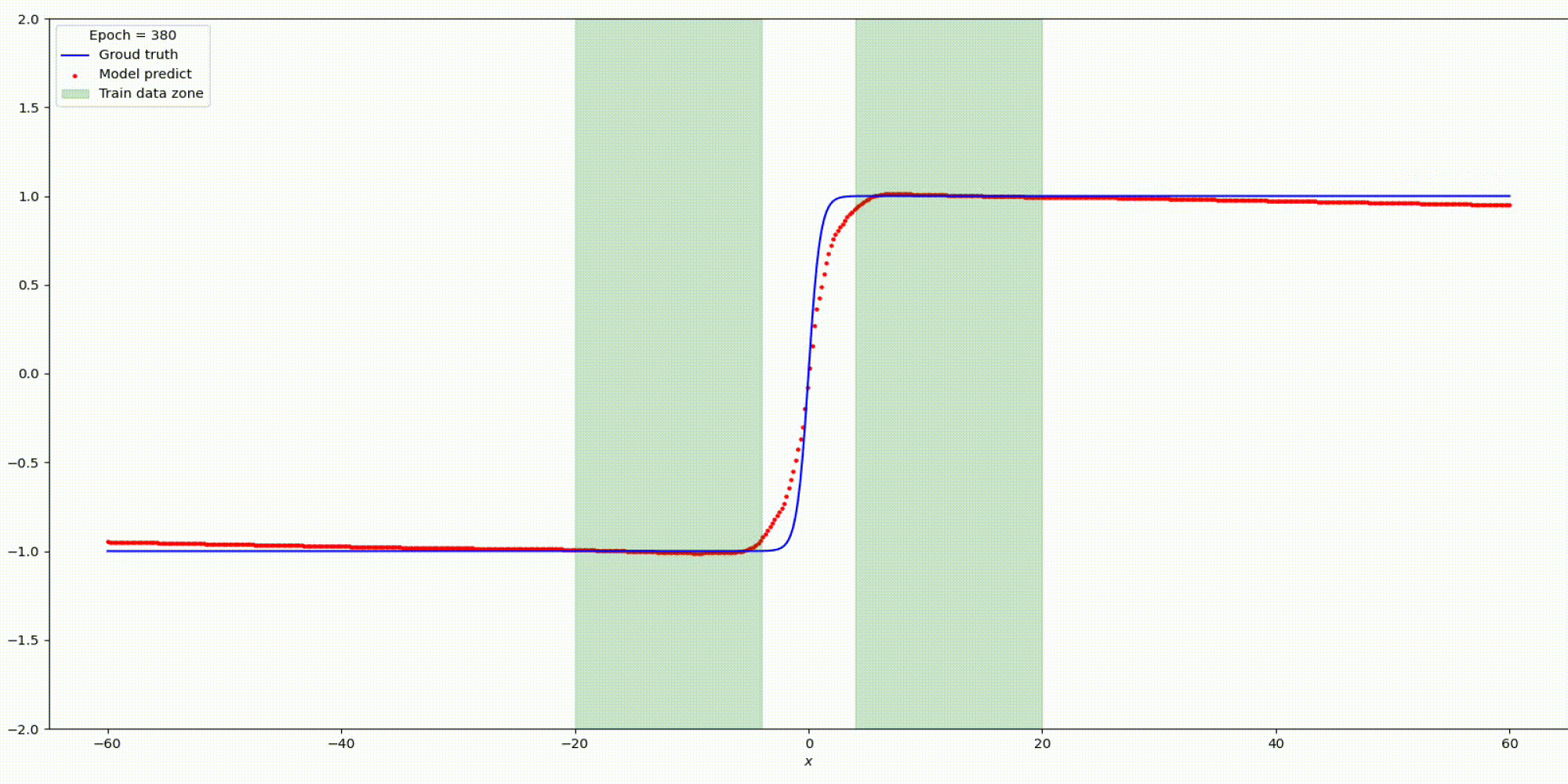

Результат на функции y=parab(x)

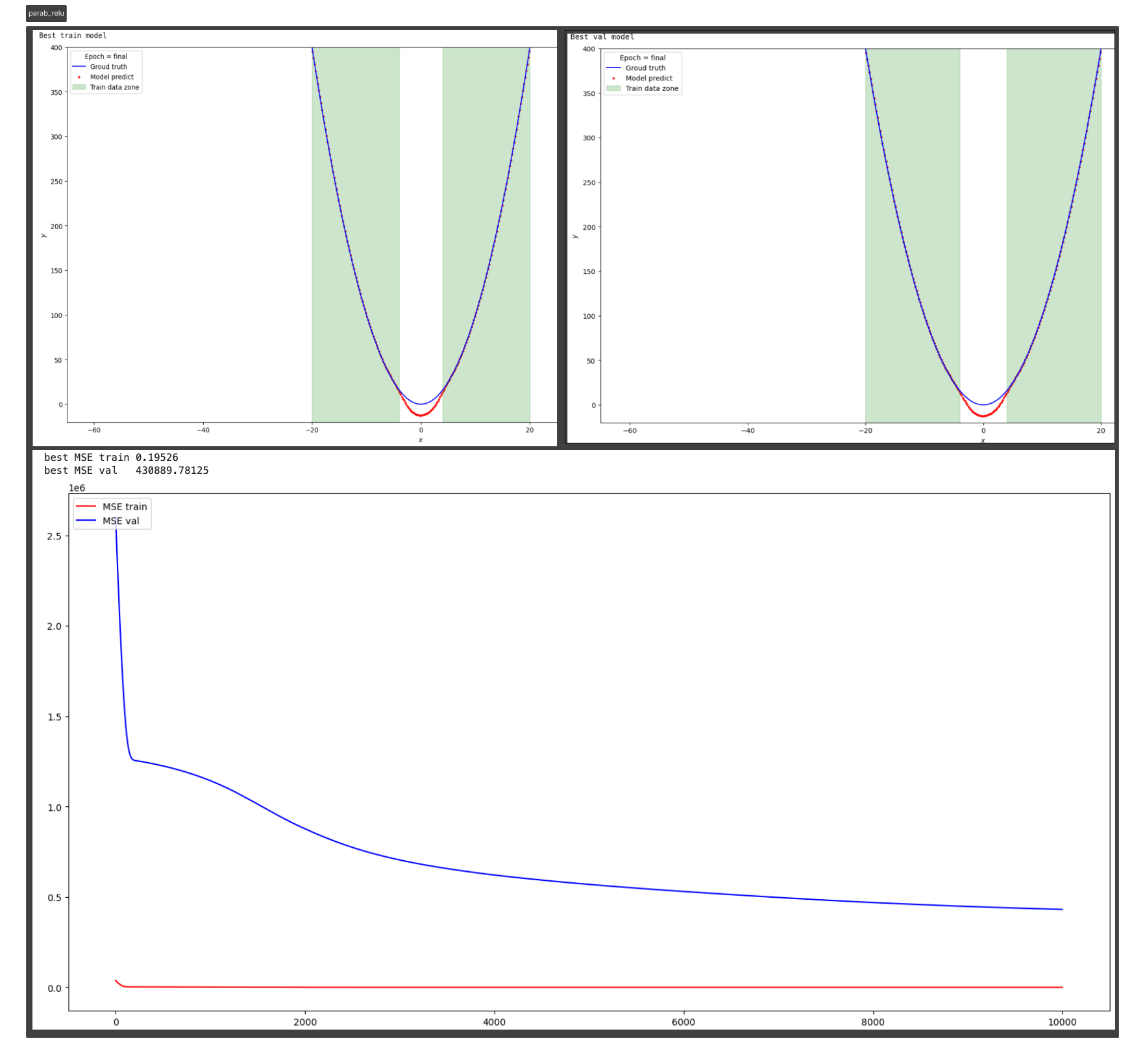
Существуют некоторые предыдущие методы, предлагающие использовать функции периодической активации (Fourier neural networks). В данном подходе предлагается использовать периодические функции, sin(x) и cos(x), или их линейные комбинации в качестве функций активации. Однако такие функции активации очень трудно оптимизировать из-за большого вырождения локальных минимумов и экспериментальные результаты показывают, что использование sin в качестве функции активации работает плохо, за исключением очень простых моделей и что оно не может конкурировать с функциями активации на основе ReLU в стандартных задача.
Для начала вспомним как выглядит функция активации Relu:

Теорема:
Рассматривая сети с прямой связью f(relu(x)) с произвольной но фиксированной глубиной и шириной d_1, .... d_h+1
где z есть вещественный скаляр, u - любой единичный вектор размерности d1 а Wu ∈ Rd1×dh - постоянная матрица, зависящая только от u.

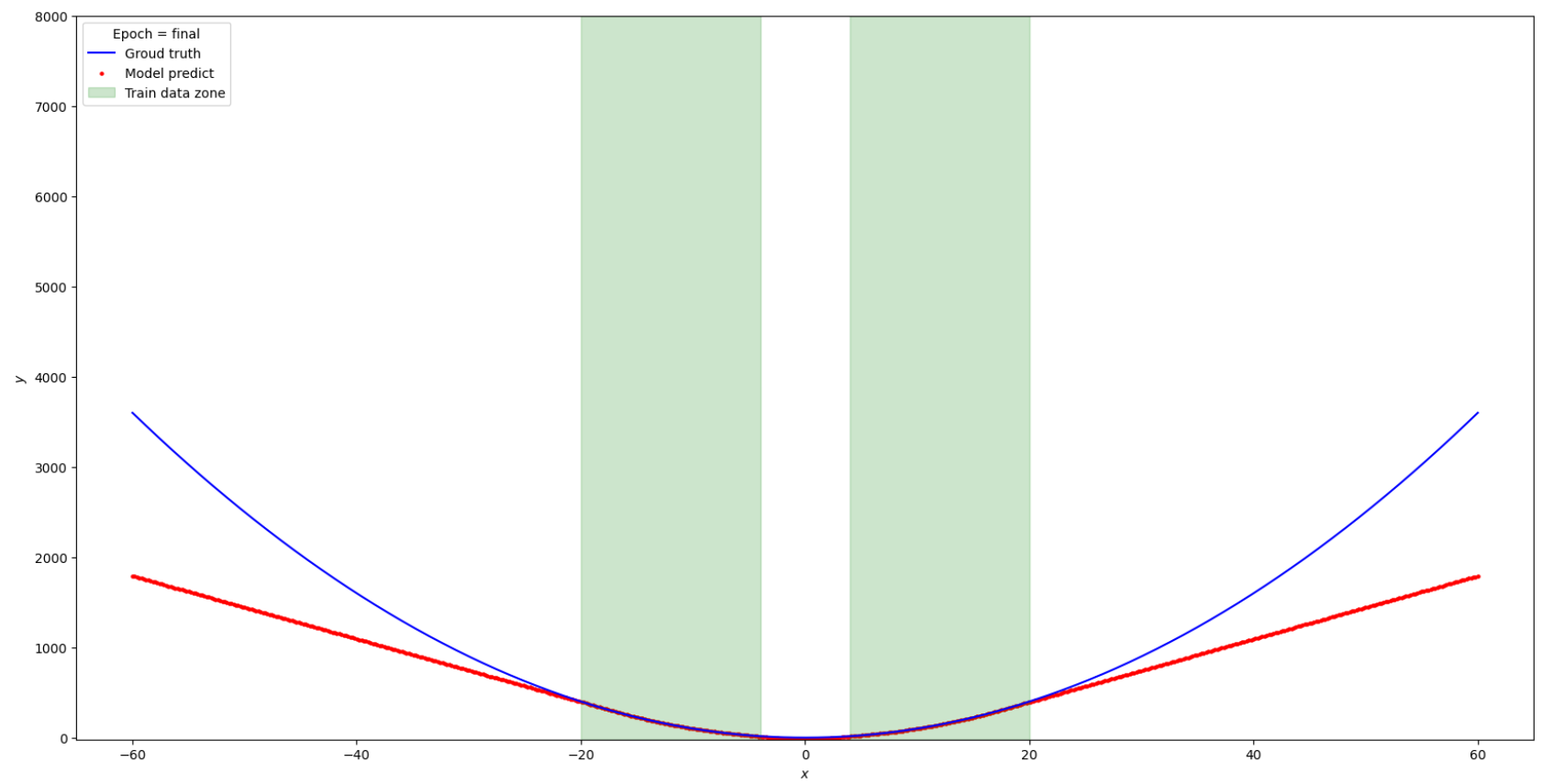
Приведенная выше теорема гласит, что любая полносвязная нейронная сеть с активацией ReLU сходится к линейному преобразованию W*u в асимптотическом пределе и это экстраполированное линейное преобразование зависит только от u. Смотрите иллюстрацию. (Не самый удачный перевод через Google Translate)
Также мы имеем понимание, что такая простая однослойная нейронная сеть Linear + Relu, при достаточном количестве нейронов, может апроксимировать с любой точностью, любую последовательность данных.
На основании предыдущих экспериментов с простыми функциями можно сделать вывод: выбор функций активации играет решающую роль интерполяционных и экстраполяционных способностях нейронных сетей и такие свойства интерполяции и экстраполяции, в свою очередь, влияют на обобщающие способности сети.
Мотивация выбора периодичной функции активации.
На ум сразу приходит взять в качестве активационной функции y=sin(x) или y=cos(x).

Однако проблема этих функций заключается не в их способности к обобщению, а в их оптимизации. На самом деле, sin не является монотонной функцией. Использование sin в качестве функции активации создает бесконечно много локальных минимумов в решениях (поскольку сдвиг "значения активации" на 2π дает та же функция), что затрудняет оптимизацию sin(x).
То есть нам нужна какая-то модифицированная sin(x), например, наклонная функция, с каким-то обучающимся параметром.

Реализацию данной функции в PyTorch позаимствовал в репозитории EdwardDixon.
Имплеминтируем в PyTorch????:
import torch
from torch import nn, sin, pow
from torch.nn import Parameter
from torch.distributions.exponential import Exponential
class Snake(nn.Module):
'''
Implementation of the serpentine-like sine-based periodic activation function:
.. math::
Snake_a := x + \frac{1}{a} sin^2(ax) = x - \frac{1}{2a}cos{2ax} + \frac{1}{2a}
This activation function is able to better extrapolate to previously unseen data,
especially in the case of learning periodic functions
Shape:
- Input: (N, *) where * means, any number of additional
dimensions
- Output: (N, *), same shape as the input
Parameters:
- a - trainable parameter
References:
- This activation function is from this paper by Liu Ziyin, Tilman Hartwig, Masahito Ueda:
https://arxiv.org/abs/2006.08195
Examples:
>>> a1 = snake(256)
>>> x = torch.randn(256)
>>> x = a1(x)
'''
def __init__(self, in_features, a=None, trainable=True):
'''
Initialization.
Args:
in_features: shape of the input
a: trainable parameter
trainable: sets `a` as a trainable parameter
`a` is initialized to 1 by default, higher values = higher-frequency,
5-50 is a good starting point if you already think your data is periodic,
consider starting lower e.g. 0.5 if you think not, but don't worry,
`a` will be trained along with the rest of your model
'''
super(Snake,self).__init__()
self.in_features = in_features if isinstance(in_features, list) else [in_features]
# Initialize `a`
if a is not None:
self.a = Parameter(torch.ones(self.in_features) * a) # create a tensor out of alpha
else:
m = Exponential(torch.tensor([0.1]))
self.a = Parameter((m.rsample(self.in_features)).squeeze()) # random init = mix of frequencies
self.a.requiresGrad = trainable # set the training of `a` to true
def forward(self, x):
'''
Forward pass of the function.
Applies the function to the input elementwise.
Snake ∶= x + 1/a* sin^2 (xa)
'''
return x + (1.0/self.a) * pow(sin(x * self.a), 2)
Сама нейронная сеть c функцией Snake:
import torch.nn as nn
class SnakeNet(torch.nn.Module):
def __init__(self, n_hidden_neurons,alpha):
super().__init__()
self.fc1 = nn.Linear(1, n_hidden_neurons)
self.act_snake = Snake(n_hidden_neurons, alpha)
self.fc2 = nn.Linear(n_hidden_neurons, 1)
pass
def forward(self, x):
x = self.fc1(x)
x = self.act_snake(x)
x = self.fc2(x)
return x
Parametrs
n_hidden_neurons=512, alpha=20, epochs=20000, lr= 0.001.
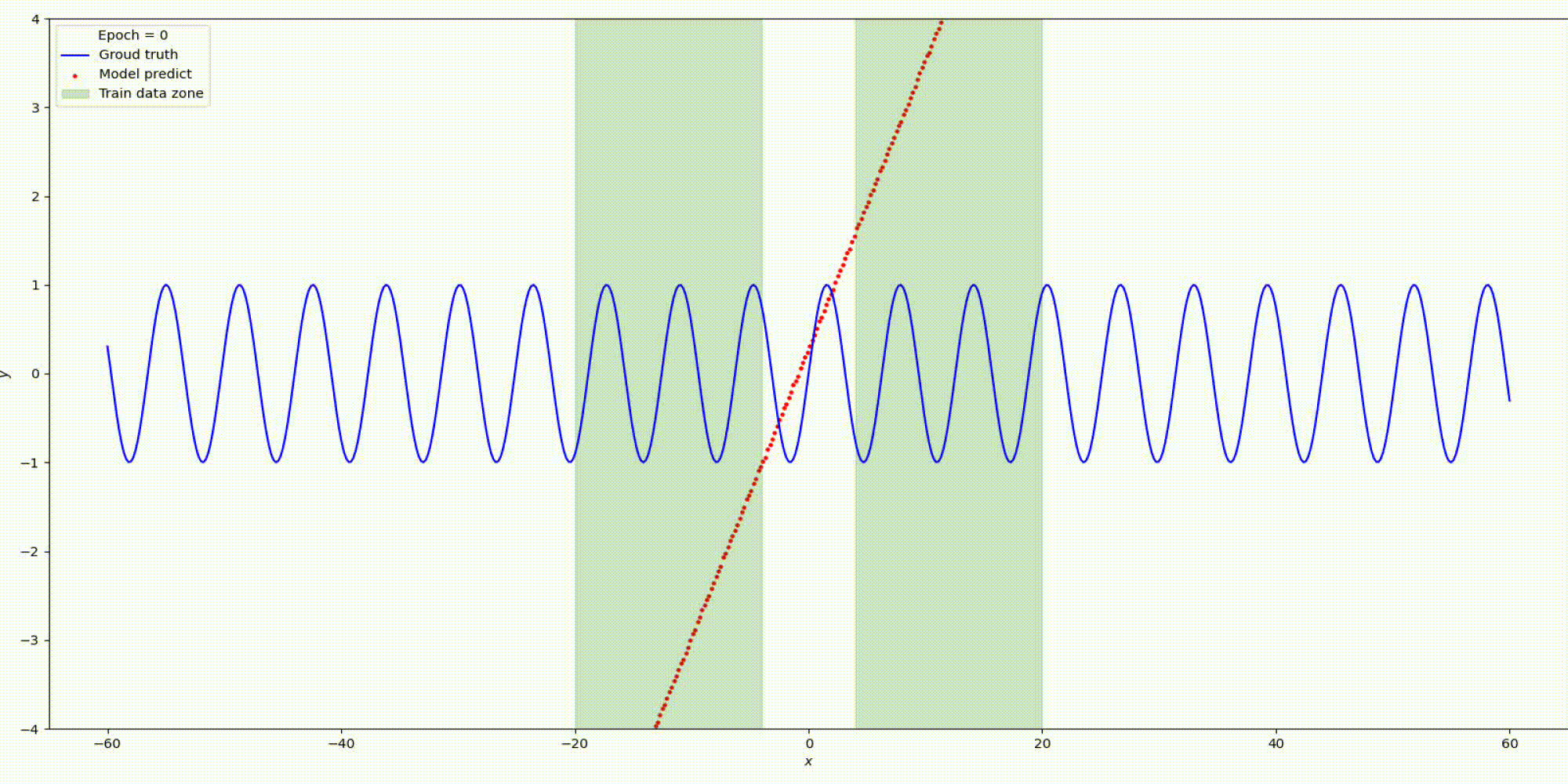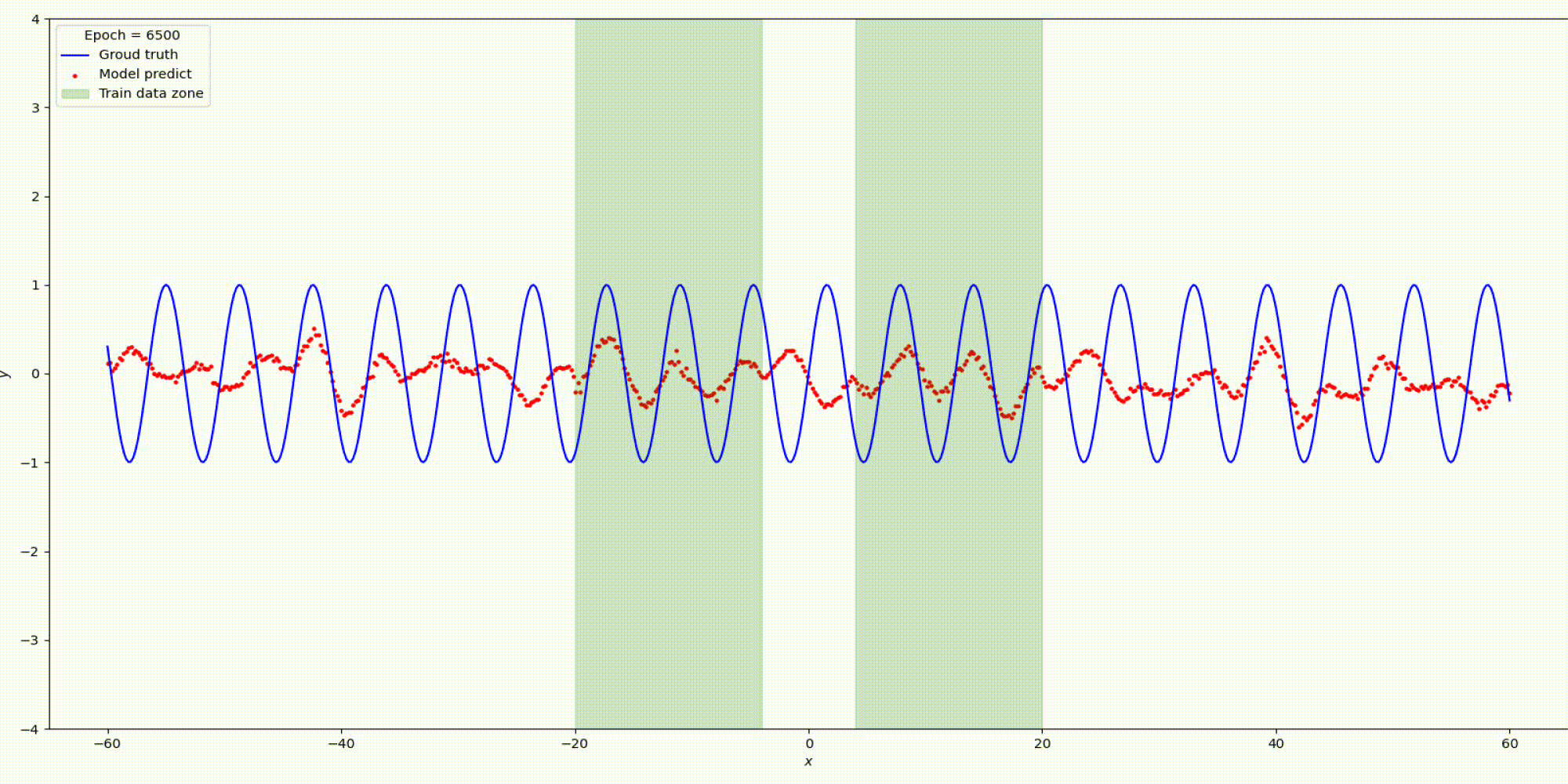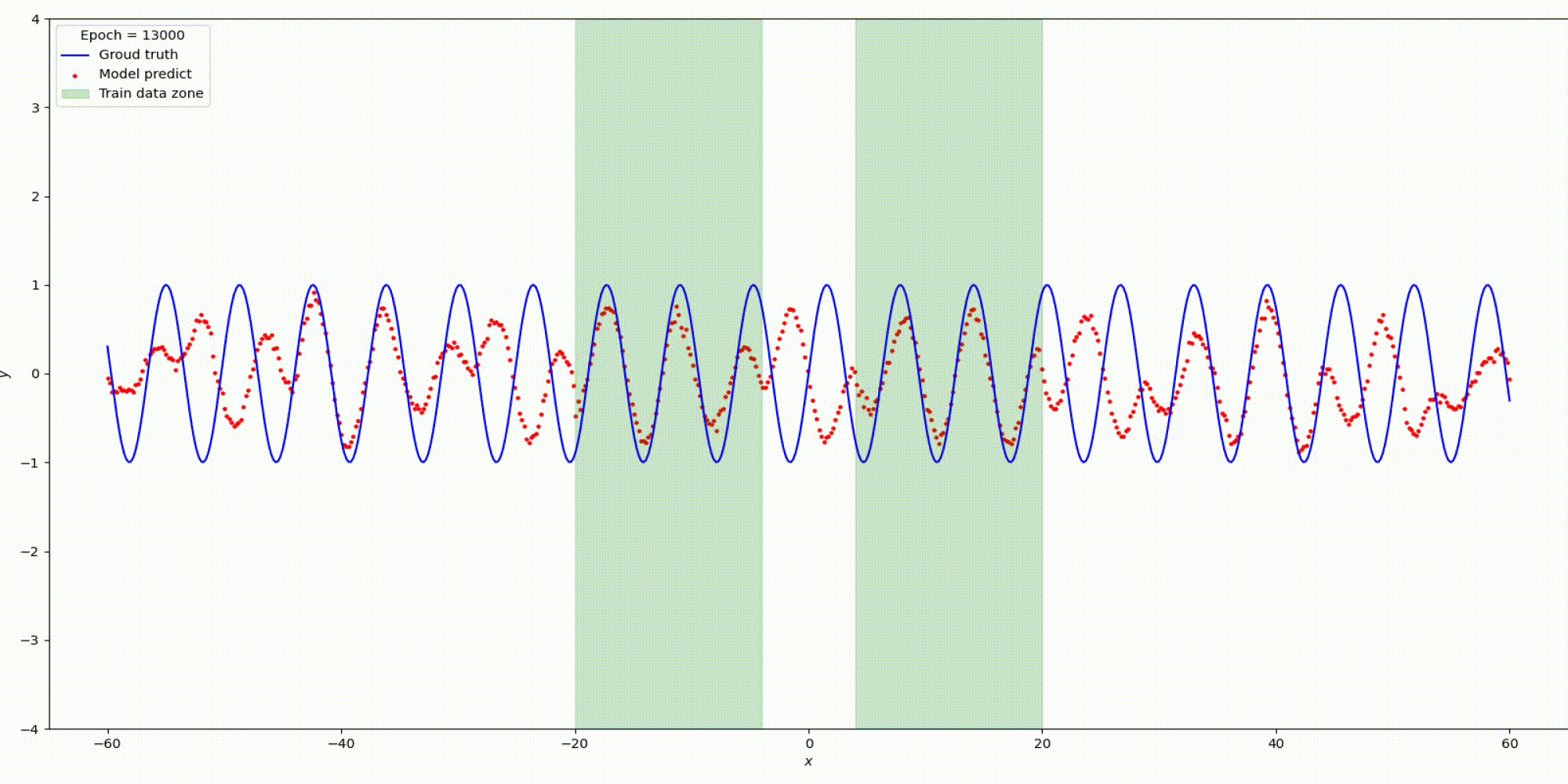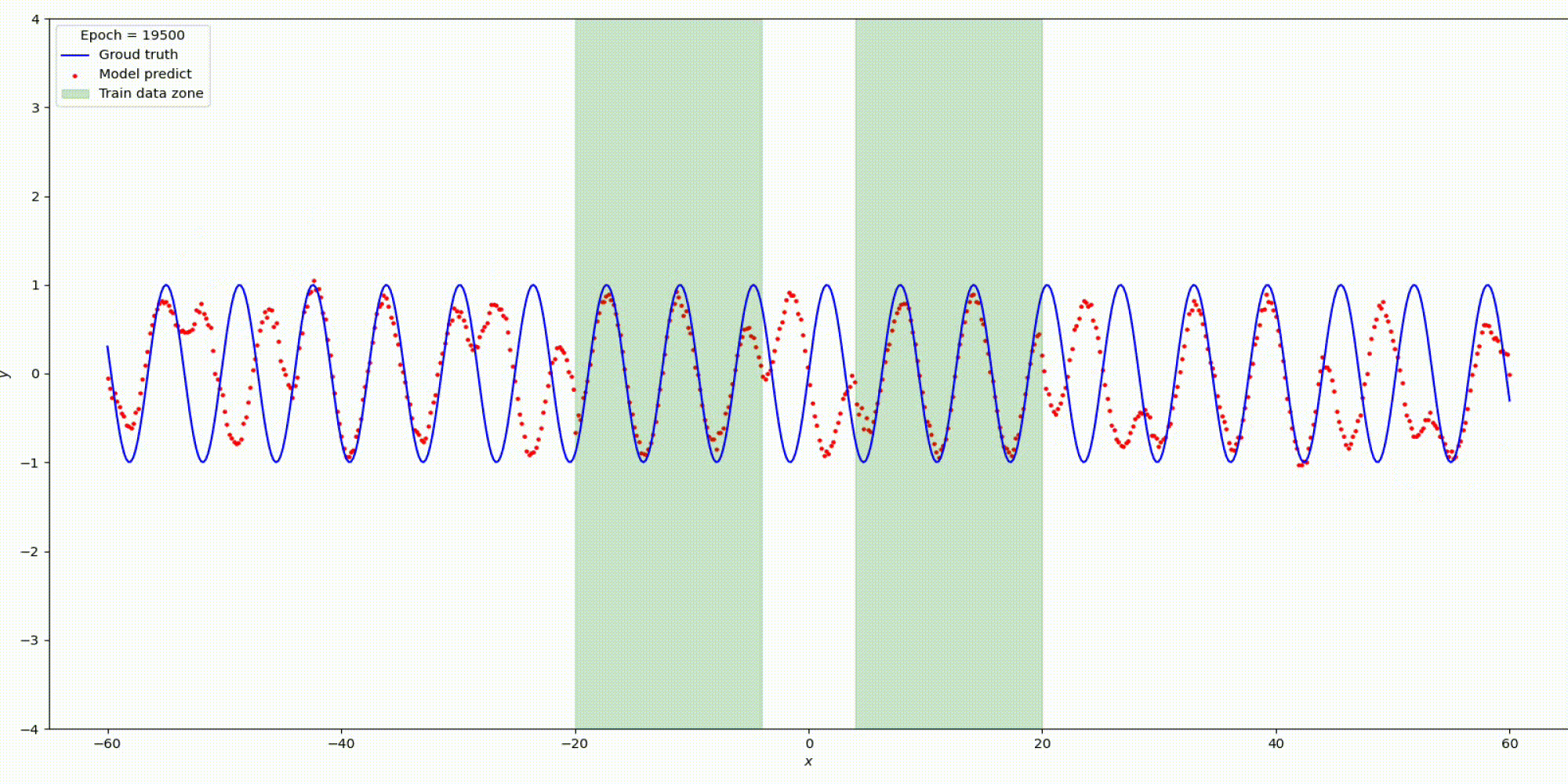

Изменим гипер-параметры
n_hidden_neurons=5, alpha=2, epochs=1500, lr= 0.0001.
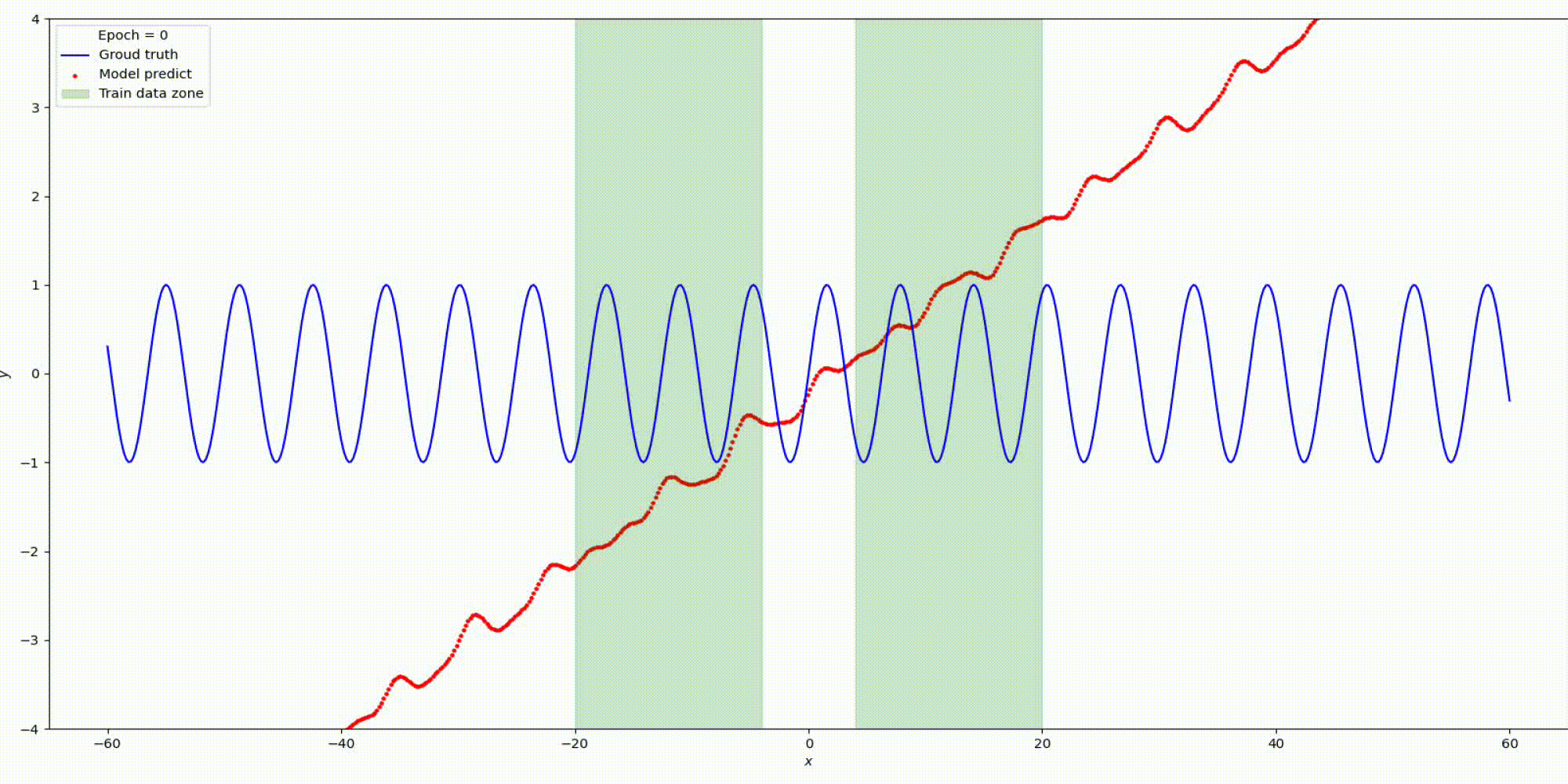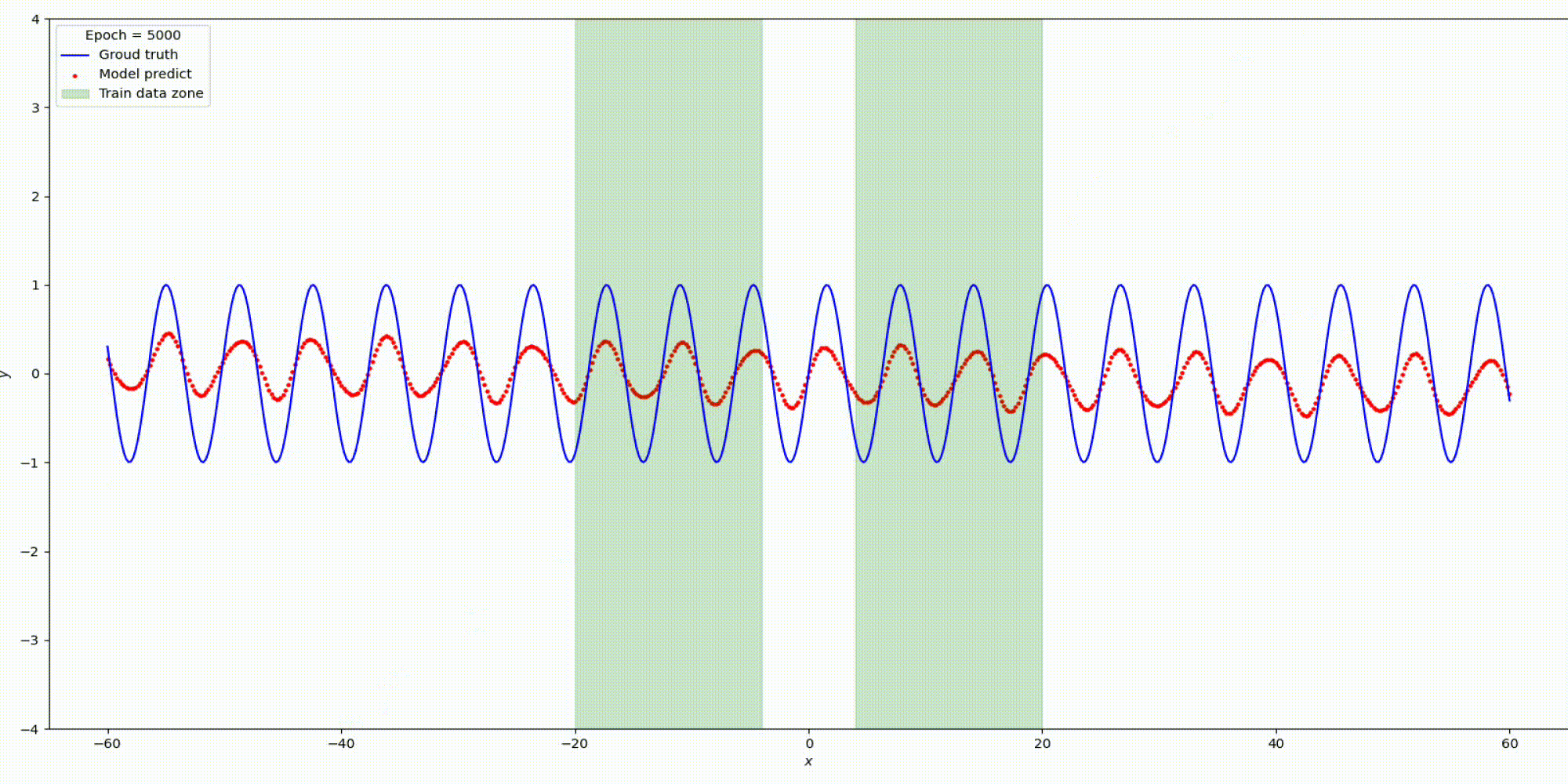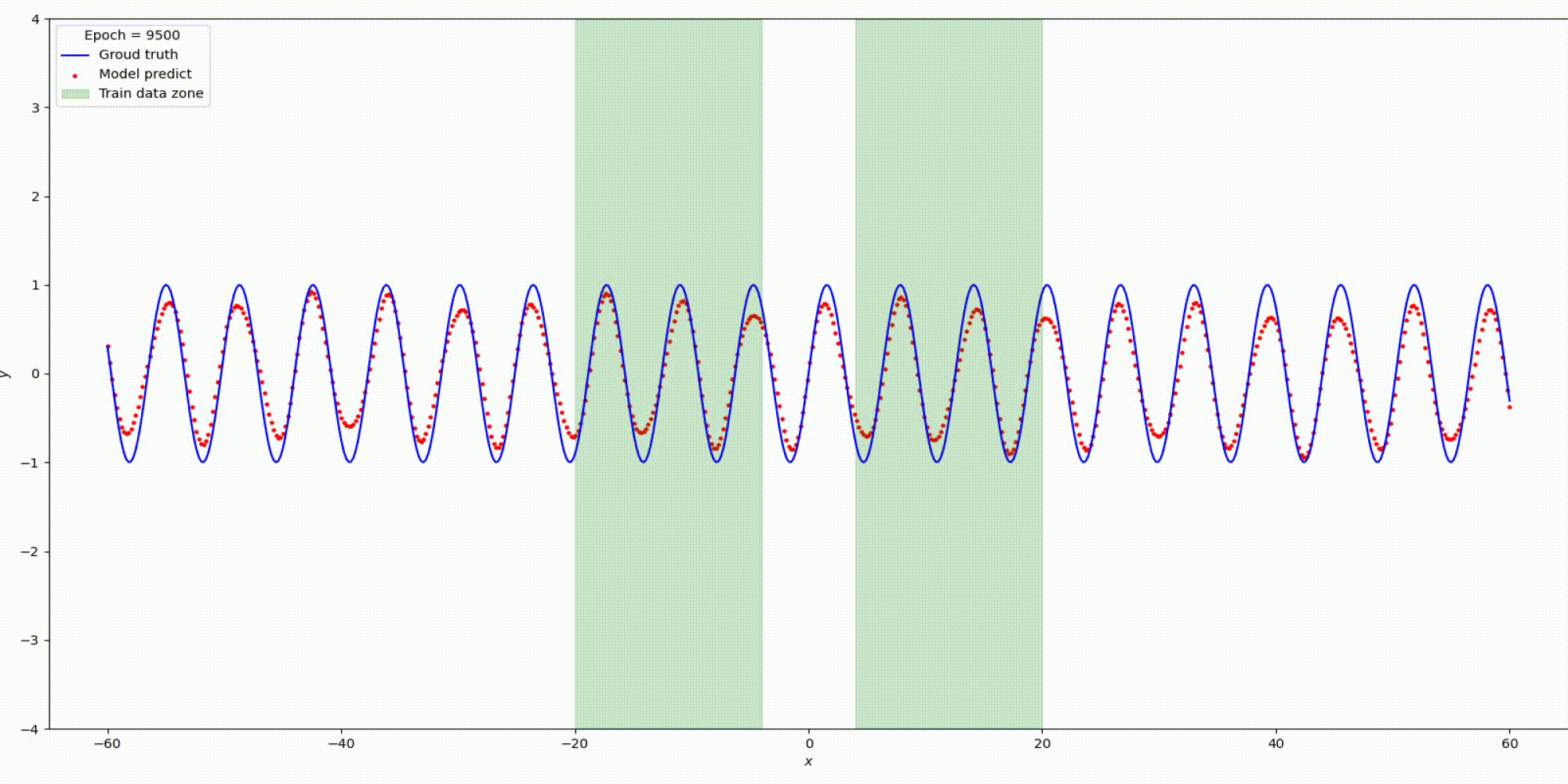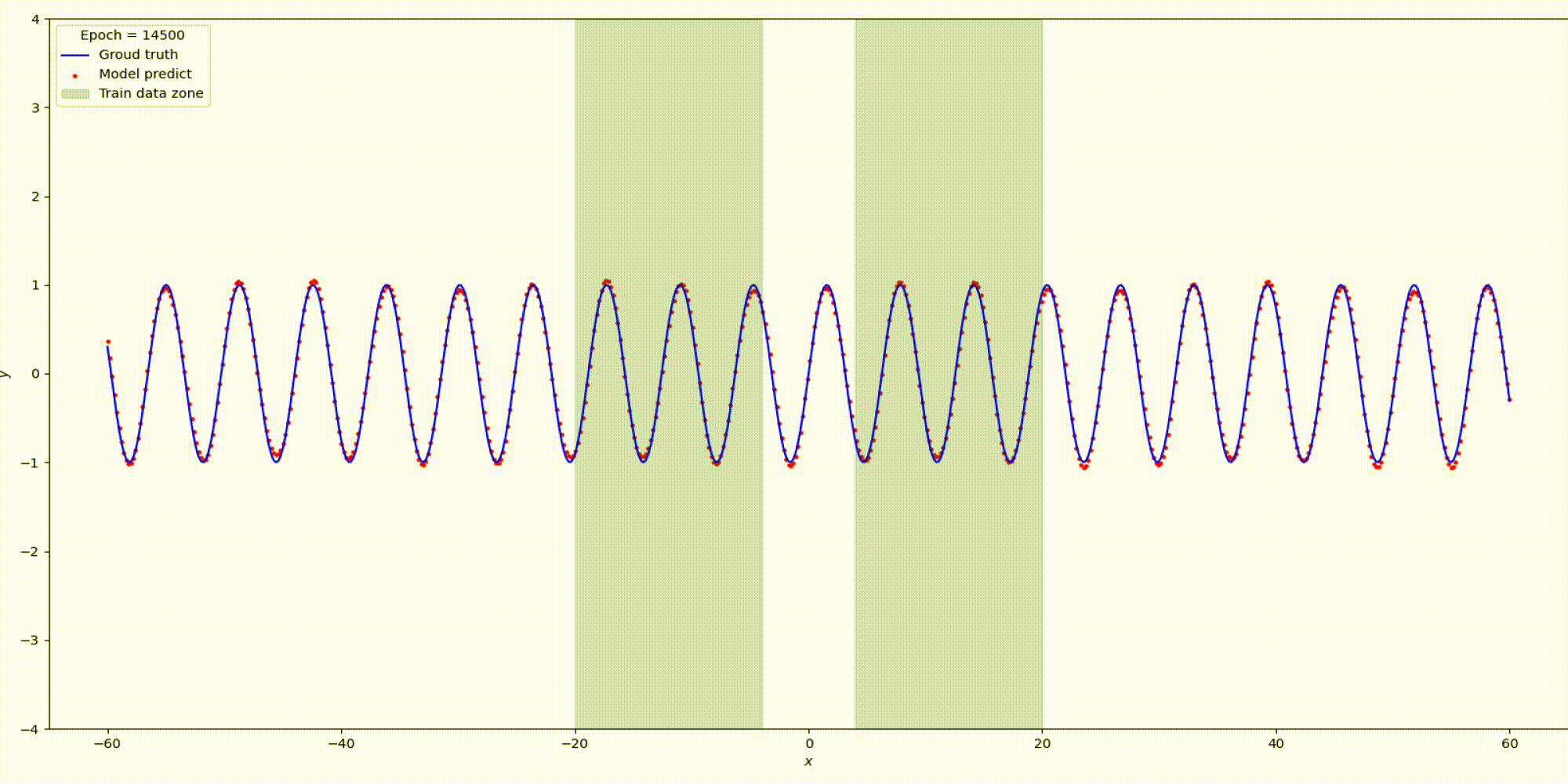
Вот что получилось
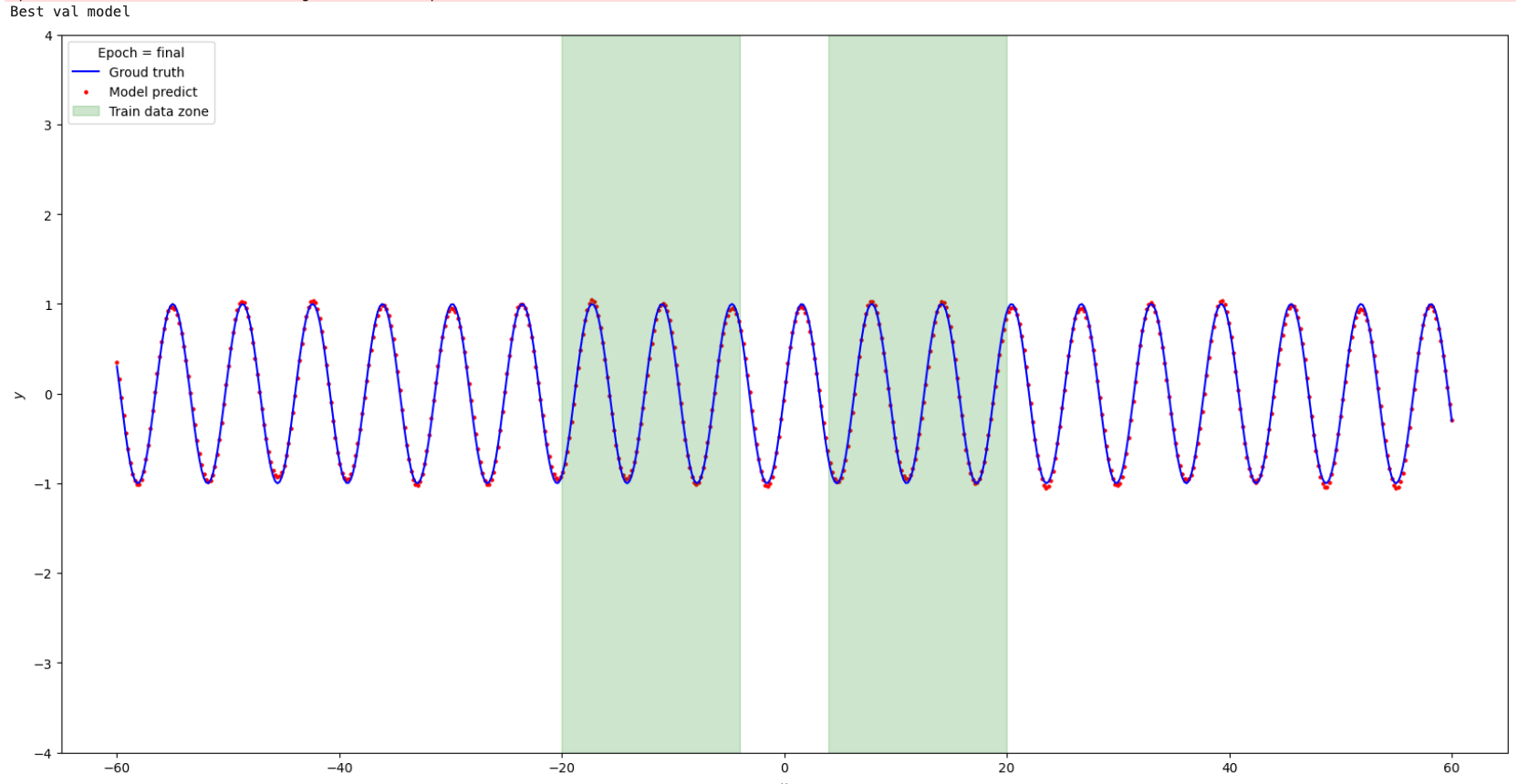
Попробуем применить ту же сеть с активацией "Snake" к параболе.

Видим, что происходит апроксимация только в районе распределения тренировочных данных, за границами обобщающие способности сети отсутствуют. Изменим конфигурацию добавив Relu + Linear. Архитектура сети: Linear -> Snake -> Linear -> ReLU -> Linear

Посмотрел, как ведет себя модель за пределами тренировочных данных, не все так хорошо. На этом я остановлюсь с простыми функциями
Сравним результаты Relu vs Snake на функции y=sin(x)
Relu neuron=500 |
Snake neuron=4, alpha=2 |
|
|---|---|---|
best MSE val |
0.49617 |
0.00119 |
Вывод из эксперементов с простыми функциями:
Данная архитектура сети, основанная на простых слоях Linear + Relu, способна находить только периодические зависимости в пределах существующего диапазона тренировочных данных. И при достаточном колличестве нейронов и глубине самой сети в теории может апроксимировать любую последовательность.
Но если в данных появляется периодическая компонента, то Linear + Relu ломается на этом и никак не может обобщать периодические зависимости в местах пространства, где данные отсутствуют - то есть экстраполировать, а в местах, где данные прерываются, Relu соединяет по прямой, тупо "интерполирует". Tahn или Sigmoid могут вносить некоторую гладкость но также не улавливают периодичность данных.
Такое же обобщение работает для функций активации Sigmoid() Tahn() Swish() и Leaky-ReLU() подобным образом как Relu.
В отличии от классических функций активации, функция Snake() может обобщать тренировочные данные и правильно экстраполировать, а значит, ее можно использовать в большем спектре задач.
Перейдем к реальным задачам:
Пытался воспроизвести и улучшить задачу, рассматриваемую в даном репозитории
Задача из категории time-series, необходимо предсказать максимальную температуру на основании данных метеостанции: давления, влажности, минимальной температуры и еще ряда параметров.

Я поигрался с разными конфигурациями сети и потюнил параметры.

На реальных данных получить каких-то выдающихся результатов не вышло : (.
Решил найти еще задачу с периодическими time series данными.
репозиторий
Формулировка проблемы:
Электроэнергетическим компаниям необходимо заранее тщательно спланировать распределение генерирующих единиц на своих электростанциях в соответствии с потребностями. Так, если спрос превышает выработку, это может привести к отключениям электроэнергии, с другой стороны, если выработка выше чем спрос, дополнительная электроэнергия будет потрачена впустую.
Таким образом, для коммунальных служб очень важно иметь прогноз потребления энергии, чтобы оптимизировать ресурсы. Прогноз на год, месяц или день вперед может помочь коммунальным службам планировать работу => фин.эффект.
Данные собранны за последние 4-10 лет:
target = количество потребления электроэнергии.
features = дата, праздник-выходной/ рабочий день, данные метеостанции - температура, влажность, дневное повышение температуры, понижение. Потребление AC - кондиционера.
У авторов этой задачи и данных есть свои неплохие решения задачи на градиентном бустинге, деревьях.
Мое решение с помощью сети:
Собрал обычную однослойную сеть без активации, по сути это линейная регрессия в имплементации торча. В качестве функции ошибки выбрал MSE-Loss.
class Net_Line_regres(torch.nn.Module):
def __init__(self, input_feature): #
super().__init__()
self.fc1 = nn.Linear(input_feature, 1)
def forward(self, x):
x = self.fc1(x)
return x
И однослойная сеть с функцией активации Snake
class Net_Snake(torch.nn.Module):
def __init__(self, input_feature, alpha):
super().__init__()
self.fc1 = nn.Linear(input_feature, 1)
self.act_snake = Snake(1, alpha)
def forward(self, x):
x = self.fc1(x)
x = self.act_snake(x)
return x
Как не бился с данными сетями, не тюнил, не переСтекивал разные слои с разными количеством нейронов, разными активациями Relu и не только, ничего дельного не получилась, даже визуально на лучших моделях достаточно большая ошибка.

Рузультаты сети Net_Line_regres: Loss = 229201.29 RMSE = 466.84 MAPE = 16.2%
Рузультаты сети Net_Snake:
Loss = 226652.28
RMSE = 463.19
MAPE = 15.4%
А теперь достаем старый добрый sk-learn, берем LinearRegression и пишем две строчки кода fit, predict.
Даже визуально видно, что модель обучилась достаточно хорошо.

Рузультаты sklearn LinearRegression:
RMSE = 254.93
MAPE = 8.38%
Мой вывод:
В своем исследовании я пытался понять основные причины, почему в общей практике не используют такие периодические функции активации:
Сложность самой функции, тк у нее бесконечное количество экстремумов.
Сложность оптимизации и вычислительная сложность, зачем так усложнять если есть Relu. Следующий интересный поинт, который лично открыл для себя. Ранее я думал, что нейронные сети, состоящие из классических слоев Linear + Activation, могут обобщать информацию и делать predict не только на том пространстве, где есть данные, но интерполируя или экстраполируя. Но как выяснил потом для себя, основная идея сетей это апроксимация, то есть приближения натягивания модели к существующим, тренировочным данным. Но я не совсем согласен с этим утверждением, тк по сути мы используем тренировочные данные, потом показываем сети валидационные, тестовые данные и хотим, чтоб она перенесла ту логику, на которой она обучилась, на те данные, которые она не видела, выходит так что тренировочные и тестовые данные должны быть ровно из того же распределения, не смещенные в пространстве. И как мы видим, данный патерн может уловить периодическая функция активации, но не Relu и не ей подобные. Поэтому я считаю, можно применять такие архитектуры для общих задач, в которых включена периодическая функция как компонента сети.
Часть 2. Перевод некоторых, интересных выжимок из статьи
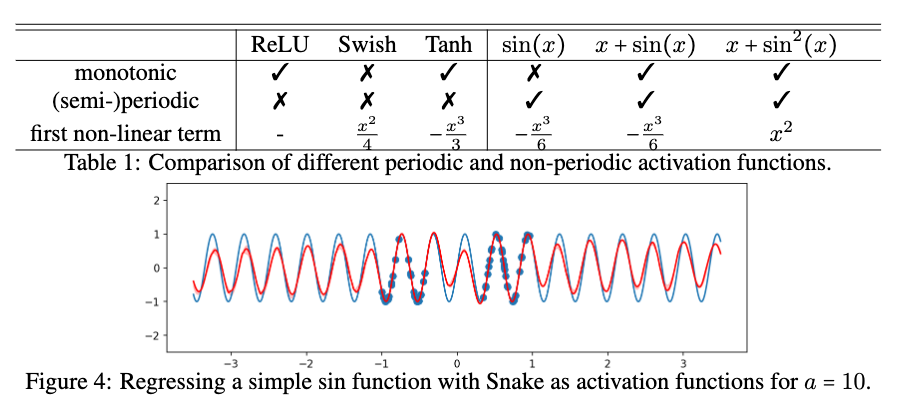
В этом разделе мы демонстрируем широкую применимость Snake. Мы начинаем со стандартной задачи классификации изображений, где показано, что Snake конкурирует с популярными функциями активации, показывая, что Snake можно использовать в качестве общей функции активации. Затем мы сосредотачиваемся на задачах, в которых, как мы ожидаем, Snake будет очень полезен, включая прогнозирование температуры и финансовых данных.
Классификация изображений:
Обучаем ResNet-18, примерно с 10 миллионами параметров, на стандартном данных CIFAR-10 - это задача классификации изображений размером 32 × 32 пикселя по 10 классам

Наша реализация воспроизводит стандартную производительность
ResNet18 на CIFAR-10, точность на тесте составляет около 92-93%. Этот эксперимент предназначен для проверки того, подходит ли Snake как универсальный инструмент для стандартных и крупномасштабных задач, с которыми приходится часто сталкиваться при машинном обучении.
Мы также сравним этот результат с другими стандартными или недавно предложенными функциями активации, включая Tanh, ReLU, Leaky−ReLU, Swish и sin.
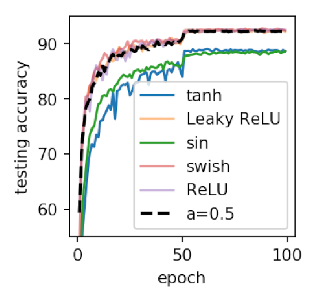
Мы видим, что функция активации sin демонстрирует те же результаты, что и tanh. В то время как Snake демонстрирует сравнительную производительность ReLU и
Leaky−RelU как в скорости обучения, так и в точности. Это указывает на то что в каких-то обобщенных задачах ReLU может быть замена на Snake
Мой комментарий: в статье не приводится, как конкретно они изменили архитектуру ResNet18, возможно они заменили Relu, а может быть сделали Relu + дополнительно еще что-то добавили, не понятно.
Прогнозирование температуры атмосферы и температуры тела человека.
Для иллюстрации мы сначала покажем два реальных применения нашего метода для прогнозирования температуры атмосферы острова и температуры человеческого тела. Это может быть очень важно для медицинского применения. Известно, что многие болезни и эпидемии имеют сильную корреляцию с температурой атмосферы, такие как атипичная пневмония и нынешний кризис COVID-19, который закончился 5 мая 2023 согласно декларации WHO. Следовательно, возможность точного моделирования температуры может быть важна для более эффективной борьбы.
Прогнозирование температуры атмосферы.
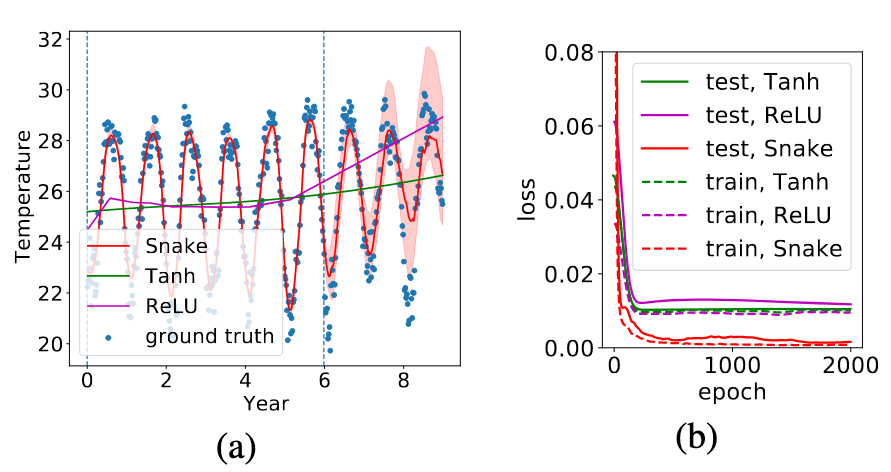
Начнем с тестирование нейронной сети с двумя скрытыми слоями (оба по 100 нейронов) для регрессии изменения температуры на Минамиторисиме, острове к югу от Токио (долгота: 153,98, широта: 24,28)3. Данные представляют собой среднюю недельную температуру после апреля 2008 года, и результаты показаны на рис. 6а. Мы видим, что модели, основанные на tanh и ReLU не оптимизируют эту задачу и не делают значимой экстраполяции, а модель на основе Snake успешно оптимизирует задачу и выполняет значимую экстраполяцию с правильными периодами. Мы видим, что сеть на базе активации Snake сводит Loss до 0 в то время как Relu, Tanh выходят на плато около 0.01 и дальнейшего уменьшения не происходит.
Прогнозирование температуры человека
Температура человеческого тела. Моделирование температуры человеческого тела также может быть важным, например, признак повышение температуры как один из наиболее важных симптомов, указывающих на инфекционное заболевание, включая COVID19. Описание эксперимента. Мы используем нейронную сеть прямого действия с 2 скрытыми слоями (оба содержат по 64 нейрона) для регрессии температуры человеческого тела. Данные были получены от анонимного участника в течение 10-дневного периода в апреле 2020 года, всего 25 измерений. Хотя этот эксперимент также является рудиментарным по своей природе, он отражает множество препятствий. В ходе эксперимента столкнулись с такими проблемами, как очень ограниченный (всего 25 измерений) набор данных. Также стоит отметить что, эксперимент проводился через нерегулярные промежутки времени.
Цель этой задачи - спрогнозировать температуру тела на каждый час. Здесь у нас нет тестового сета для решения этой задачи, поскольку весьма маловероятно, что модель правильно спрогнозирует решение этой задачи из-за больших колебаний температуры человеческого тела. На самом деле, у нас есть некоторые базовые знания о температуре тела.
Например, температура должна находиться в разумных пределах от 35,5 до 37,5 градусов Цельсия и по сути, именно в этом диапазоне находятся все точки тренировки. Как минимум, модель должна подчиняться этому правилу, и достаточно хорошо обученная модель также должна обнаруживать колебания в течении дня, когда мы спим и активничаем.
Однако tanh или ReLU не могут ограничить температуру до диапазона 35,5 и 37,5 градуса. Обе исходные линии экстраполируются до уровня выше 39 градусов через 20 дней после
выборки train-set. Напротив, обучение со Snake в качестве функции активации научило подчиняться некоторым априори известным правилам.

Прогнозирование фондового индекса Wilshire 5000
Постановка проблемы. Глобальная экономика - это еще одна область, где может происходить квазипериодическое поведение.
На микроскопическом уровне экономика колеблется сложным, непредсказуемым образом; на макроскопическом уровне глобальная экономика следует 8-10-летнему циклу, который переходит между периодами роста и рецессии. В этом разделе мы сравниваем различные модели для прогнозирования общей рыночной капитализации США, измеряемой с помощью индекса полной рыночной капитализации Wilshire 5000 (также провели этот же эксперимент с хорошо известным индикатором Buffet, который рассматривается как сильный индикатор для прогнозирования национальной экономической тенденции; мы также видим аналогичные результаты). Для обучения мы берем ежедневные данные из с 01-01-1995 по 31-01-2020, в общей сложности около 6300 пунктов, время окончания намеренно выбрано таким образом, чтобы оно наступило до того, как COVID19 начнет оказывать влияние на мировую экономику. Мы используем данные периода от 01-02-2020 до 31-05-2020 в качестве тестового сета. Примечательно, что тестовый набор отличается от обучающего несколькими значимыми факторами. Происходит рыночный спад, называемый черным четвергом (см. рис.); общая тенденция носит рецессивный характер (рыночная капитализация в среднем снижается). Интересно посмотреть, предсказуем ли медвежий тренд в этот период без влияния COVID19. Для методов, основанных на нейронных сетях, мы используем 4-слойную полносвязную сеть с 1 → 64 → 64 → 1 скрытыми нейронами, с указанной функцией активации, мы отмечаем, что ни одна функция активации, кроме Snake, не может быть оптимизирована до сведения функции loss практически в 0 при обучении.
Method |
MSE on Test Set |
|---|---|
ARIMA (2,1,1) |
0.0215±0.0075 |
ARIMA (2,2,1) |
0.0306±0.0185 |
ARIMA (2,2,1) |
0.0282±0.0167 |
ARIMA (2,1,2) |
0.0267±0.0154 |
ReLU DNN |
0.0113±0.0002 |
Swish DNN |
0.0161±0.0007 |
sin + cos DNN |
0.0661±0.0936 |
sin DNN |
0.0236±0.0020 |
Snake |
0.0089±0.0002 |

Результаты: Смотрите таблицу выше, мы видим, что предложенный метод значительно превосходит конкурентов в прогнозировании рыночной стоимости на период 2020-2021 годов. Мы фокусируемся на сравнении с ARIMA, традиционным и стандартным методом в экономике и прогнозировании цен на акции. Смотрите рисунок 8. Мы отмечаем, что ARIMA предсказывает растущую экономику, Snake предсказывает рецессивную экономику начиная с 2020-2021 годов. Фактически, для всех методов, приведенных в таблице 2, предлагаемый метод является единственным методом, который предсказывает спад во время тестирования и после его завершения период, мы предполагаем, что это связано с тем, что предлагаемый метод является единственным методом, который учит улавливать долгосрочные экономические циклы в тренде. Кроме того, интересно, что модель предсказывает рецессию, не предсказывая сильного обвала рынка. Это может свидетельствовать о том, что обвал рынка вызван влиянием COVID19, в то время как одновременно происходит фоновая рецессия, потенциально обусловленная глобальным деловым циклом. Исключительно в целях анализа мы также даем прогноз до 2023 года на рисунке 8. Вызывает тревогу тот факт, что наш метод предсказывает долгосрочную глобальную рецессию, начиная с мая 2021 года, в среднем на 1,5-летний период, который заканчивается только примерно в начале 2022 года. Это также говорит о том, что COVID19 может быть не единственной причиной нынешнего спада в экономике.
Вывод
В этой работе мы определили свойства "экстраполяции" как ключевой компонент для понимания оптимизации и обобщения нейронными сетями различных данных. Наше исследование экстраполяционных свойств нейронных сетей со стандартными функциями активации предполагает отсутствие возможности заучивания периодической функции: из-за несогласованного индуктивного смещения оптимизация затруднена, а обобщение за пределами диапазона наблюдаемых точек данных не удается. Мы думаем, что эти факторы говорят о том, что экстраполяционные свойства нейронных сетей должны заслуживать гораздо большего внимания, чем им уделяется в настоящее время.
Комментарии (5)

aaa_bbb
04.07.2023 08:50+4когда-то изучал МГУА. Для периодических функций там был специальный алгоритм - "Гармонический".
Периодическая модель представлялась в виде суммы моделей: гармонический тренд и остаток .
Полагаю, если мы уверены что моделируем периодический процесс (как энергопотребление), то можно смоделировать тренд другим алгоритмом, а с остатком уже баловаться различными нейронками.

S_A
04.07.2023 08:50+1Что-то не очень исправило. Примеры из статьи на тоненького.
Естественно сетки интерполируют, как и все остальные алгоритмы. И брать тощую сетку и делать глобальные выводы... Спорно. К тому же есть два момента
рекуррентные выучивают периодические паттерны, и трансформеры тоже. Кстати они Тьюринг-полные, хотя и на relu, и это важно по мне как. Они выучивают "программу дата генерации",
-
экстраполяция - это та же интерполяция, только в пространстве без дрейфа. Статья - попытка перейти в это пространство. Не специфицируя его явно. Этим она хороша.
От прочтения вашей статьи тем не менее удовольствие испытал, и обогатился идеями, спасибо

S_A
04.07.2023 08:50+1Чуть дополню себя. Теорема странноватая, а вывод и без нее понятный...
Понятно что один слой с relu даст линейное преобразование практически - из-за bias. То что нелинейность важна - так в этом и суть сеток. Все это про частный случай сеток - которые и появились для нелинейности.
Но сама идея x + sin(x)**2 отличная, есть где поиграться. Я как-нибудь попробую relu(x + alpha * sin(x / alpha)**2). Рассчитываю что докинет, причем в более мелкую сетку.

berng
04.07.2023 08:50+1Насчет "не могут" - неверно. Полносвязные предельно малой глубины возможно не могут. Но существует куча архитектур, от рекуррентных до сверточных, которые легко "могут". И существуют теоремки, которые доказывают, что узкие, но глубокие полносвязные сети тоже могут, в том числе и с сигмоидной и relu активациями. Иначе зачем-бы весь этот хайп вокруг нейронок.
А snake - да, интересная активация, пару лет как использую.


nikolz
Мое субъективное мнение: Подобную задачу экстраполяции решают жидкие нейронные сети .
---------------------------
Вопрос: А Вы не пробовали без нейронных сетей решить задачу экстраполяции путем фильтрации сигнала или методом главных компонент.
Ну или хотя бы брать первичные признаки в спектральной области.