Диффузионные модели в CV. Что за зверь? / forpes.ru

24.10.2023 08:44

Kit_Cat 0 3800 Источник

Всех приветствую! Генеративные модели сейчас находятся на хайпе и про них слышно из каждого угла. Многие знакомы с Dalle-2, Dalle-3, Midjourney, Stable AI и это лишь модели из домена по генерации изображений. Можно перечилить еще десяток моделей из другого домена, как звук, видео, текст. Я буду опираться конкретно на компьютерное зрение, так как понимаю в этом чуть больше, нежели в других доменах.

Несколько лет назад при слове генерация, в голове всплывали слова типа GAN, вариационные автоэнкодеры (могу говорить только за себя). Но сейчас они отошли на второй план и в основе многих генеративных моделей лежат, как уже очевидно следует, из названия статьи диффузионные модели. Попытаемся разобраться что это такое и как с этим работать.

Если объяснять в двух словах, то идея заключается в следующем: берем картинку, постепенно добавляем к ней шум в течении некоторого количества шагов, а после обучаем нейронку восстанавливать из зашумленной картинки исходную.

Ниже приведу картинку для наглядности.

Не обращаем внимание на математические обозначения, обо всем попорядку

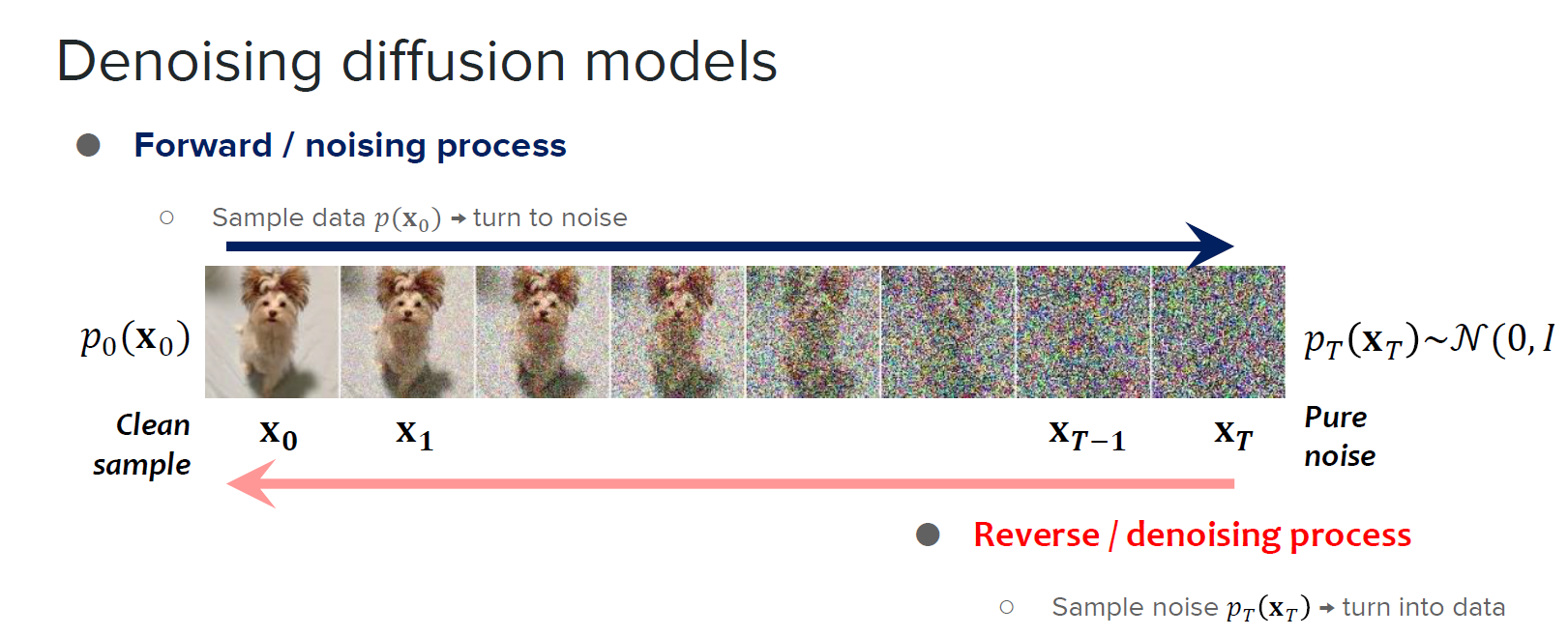
Попытки сгенерировать идею работы диффузионных моделей в CV с помощью Bing 3

Не понятные слова, но схема выглядит красиво. Жаль, что бесмысленно

База

Теперь копнем по глубже. Начнем с определения диффузионной модели:

Диффузионные вероятностные модели это класс генеративных моделей, идея которых взята из неравновесной термодинамики (non-equilibrium thermodynamics). В основе лежит цепь Маркова, которая медленно добавляет шум к данным, а затем обращает процесс диффузии в спять, чтобы получить исходные данные. Целью является выучить процесс диффузии для генерации вероятностного распределения данных, которые мы используем в задаче. Есть три основных этапа: forward process, reverse process.

Данные представляются в виде последовательности шагов, где каждый шаг представляет собой переход от одной точки данных к другой. На каждом шаге данные подвергаются некоторому уровню "размытия" или случайного шума, что соответствует процессу диффузии.

Диффузия - это фундаментальный процесс, который описывает распространение вещества или информации от области с более высокой концентрацией к области с более низкой концентрацией. Пример из физики, от теплопроводности материала зависит скорость тепловой диффузии (медь/сталь/алюминний быстро нагреваются). Но где же здесь место для "шума"/"размытия"? В терминах тепловой диффузии "размытие" данных не применимо, вместо этого мы имеем диффузионный процесс, который изменяет физические параметры, мы говорим о перемещении молекул или частиц, их скоростях и температурных изменениях. Еще одним примером диффузионного процесса является Броуновское движение.

Модели диффузии часто основаны на идее диффузии частиц, где частицы распространяются в пространстве и времени. Эти модели могут быть связаны с уравнением теплопроводности, если мы рассматриваем диффузию вещества или изменение концентрации. Они также могут быть связаны с уравнением Фоккера-Планка, которое описывает изменение вероятности местоположения частиц.

Эти уравнения можно использовать для анализа и моделирования распространения частиц в жидкости. Но кажется, мы начинаем слишком углубляться в физику, а нам это не нужно, вернемся к компьютерному зрению.

Компоненты диффузии

Повторюсь в моделях есть 2 основных процесса при обучении: forward и reverse. Давать определения я им не буду, очевидно, что они означают. Посмотрим на них с математической точки зрения.

Диффузионные модели относятся к классу статистических моделей, которые используются для прогнозирования плотности вероятности в определенный момент времени. Прогнозирование плотности вероятности в момент времени t зависит только от непосредственного предшественника в момент времени t-1.

Пусть у нас есть распределения данных q(x). Количество шагов в прямом процессе обозначим как T. Процесс изменения данных контролируется variance schedule (обозначают как бета). Своего рода это план как будет менятся данные. Параметр бета отвечает за то, как сильно мы будем зашумлять изображение. Чем больше шагов мы сделаем, тем более шумное будет изображение.

$\begin{aligned} q(\mathbf{x}_t \vert \mathbf{x}_{t-1}) &= \mathcal{N}(\mathbf{x}_t; \sqrt{1-\beta_t} \mathbf{x}_{t-1}, \beta_t)\mathbf{I} \end{aligned}$

В итоге можно прийти к этому.

$\begin{aligned} q(\mathbf{x}_t \vert \mathbf{x}_0) &= \mathcal{N}(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t)\mathbf{I}) \end{aligned}$

Откуда альфа? Во всех изученных статья приводилось замена переменной alpha = 1 - beta. После всех попыток узнать зачем, ответа найдено не было. Возможно, для упрощения или для выбора степени стохастичности или детерминированности. Кто знает, подскажите, пожалуйста, интересно. Вопрос: Как мы приходим к формуле выше? Мы знаем среднее и дисперсию, получаем:

$\begin{aligned} \mathbf{x}_t &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1} \end{aligned}$

=Если последовательно расписать процесс, то станет очевидно, кака в итоге мы пришли к формуле.

$\begin{aligned} \mathbf{x}_t &= \sqrt{\alpha_t}\mathbf{x}_{t-1} + \sqrt{1 - \alpha_t}\boldsymbol{\epsilon}_{t-1}=\\ &= \sqrt{\alpha_t \alpha_{t-1}} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t \alpha_{t-1}} \bar{\boldsymbol{\epsilon}}_{t-2} \\ &= \dots \\\end{aligned}=$

Весь этап зашумления можно представить так:

Параметр бета может меняться из шага в шаг или оставаться статичным. Параметр βτ может быть использован для контроля уровня стохастичности или интенсивности случайного шума в системе. Например, при более высоком значении βτ, случайный шум будет иметь большее влияние на систему, что может привести к большей вариабельности и случайности в движении системы. С другой стороны, при более низком значении βτ система будет более стабильна и менее подвержена случайным изменениям.

Параметр βτ

Параметр βτ может быть как числовым значением, так и функцией, в зависимости от контекста и спецификации модели.

Числовое значение: В некоторых случаях параметр βτ может быть задана как константа, которая не меняется в процессе моделирования. Например, можно установить βτ = 0.5 или βτ = 1.0.
Функция: В других случаях параметр βτ может быть функцией, которая изменяется со временем или по другим критериям. Например, можно определить βτ как сигмоидную функцию, где значение βτ постепенно изменяется от низких значений к высоким значениям в зависимости от времени или других переменных. Это позволяет моделировать изменение степени стохастичности или интенсивности случайного шума в системе в процессе времени.

Итак: бета представляет долю стоахастичности модели, а значение 1-бета долю детерминированности.

Когда βτ = 0, это означает, что в модели отсутствует стохастичность и весь процесс является полностью детерминированным.
Когда βτ = 1, это означает, что стохастичность играет полностью случайную роль в модели, и все состояния системы определяются случайными флуктуациями.
Если βτ находится между 0 и 1, то модель содержит и стохастическую, и детерминированную составляющую.

Динамика Лангевина

Динамика Ланжевена - это концепция из физики, разработанная для статистического моделирования молекулярных систем. В контексте вероятностного моделирования, динамика Ланжевена используется для генерации выборок из вероятностных распределений, основываясь на градиенте логарифма плотности вероятности. Она представляет собой стохастическую динамику, в которой частицы (или состояния системы) движутся под влиянием силы, направленной в сторону наиболее вероятных областей пространства состояний.

В применении к стохастическим моделям, таким как диффузионные модели, динамика Ланжевена используется для обновления состояний системы. Градиент плотности вероятности выступает в качестве "силы", которая определяет направление движения состояний.

Градиент плотности вероятности (gradient of the probability density) является векторным оператором, который указывает на направление и интенсивность наиболее быстрого изменения плотности вероятности в пространстве состояний. Если значение компоненты градиента положительное, это указывает на то, что плотность вероятности возрастает в этом направлении, а если значение отрицательное, то плотность вероятности убывает.
Итог: обновляем состояние ситемы в правильном направлении, так как движемся в сторону большей вероятности.

$\mathbf{x}_t = \mathbf{x}_{t-1} + \frac{\delta}{2} \nabla_\mathbf{x} \log p(\mathbf{x}_{t-1}) + \sqrt{\delta} \boldsymbol{\epsilon}_t$

где δ - шаг времени, определяющий интервал между обновлениями состояния.

Reverse process

Мы представляем, что у нас есть некоторое распределение р с параметрами среднее и отклонение, которое надо выучить. Это распределение будет выучивать нейронная сеть. (выучивать среднее и отклонение, как у вариационного энкодера)

Нам необходимо вспомнить формулу Байеса.

$\begin{aligned} p({x}_{0:t-1} \vert \mathbf{x}_t) &= \frac {p(x_t)} {p(x_{0:t})} = \frac {p(x_t)p(x_t \vert x_{0:t-1})}{p(x_{0:t-1})} \\ p_{\theta} (x_{0:T}) &= p(x_T) \prod^T_{t=1} p_{\theta} (x_{t-1} \vert x_t) \\ p_{\theta} (x_{t-1} \vert x_t) &= \mathcal{N}(x_{t-1} ; {\mu}_{\theta}(x_t, t), \sum{_\theta}(x_t, t)) \end{aligned}$

Используя формулу Байеса и для упрощения логарифмируем правую часть.

$\begin{aligned} p(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= p(\mathbf{x}_t \vert \mathbf{x}_{t-1}, \mathbf{x}_0) \frac{ p(\mathbf{x}_{t-1} \vert \mathbf{x}_0) }{ p(\mathbf{x}_t \vert \mathbf{x}_0) } \\ \end{aligned}$

Не буду приводить здесь большое количество формул, так как это только может напугать. В ходе разложения правой части в конечном итоге получим:

$\begin{aligned} q(\mathbf{x}_{t-1} \vert \mathbf{x}_t, \mathbf{x}_0) &= \exp\Big( -\frac{1}{2} \big({(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}})} \mathbf{x}_{t-1}^2 - {(\frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0)} \mathbf{x}_{t-1} + \\ {+C(\mathbf{x}_t, \mathbf{x}_0) \big) \Big)} \\ {\boldsymbol{\mu}}_t &= \frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} x_0 \\ {\beta}_t &=(\frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}}) \end{aligned}$

Известно, из функции плотности нормального распределения, что среднее равно 0, а дисперсия 1.

$\begin{aligned} std &= \frac {1}{\beta}=1; \\ mean &= \frac {\mu}{\beta}=0; \end{aligned}$

В ходе применения математических операций и упрощения, получим следующее приблизительные значения среднего и дисперсии. Почему приблизительные, потому что параметры альфа и бета обучаемы и в идеале наше среднее и дисперсия должна быть равно 0 и 1 или хотя бы стремится к нулю и единице.

$\begin{aligned} \tilde{\boldsymbol{\mu}}_t &= {\frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big)} \\ \tilde{\beta}_t &= {\frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \cdot \beta_t} \end{aligned}$

Нейронная сеть должна предсказывать именно это: среднее и дисперсию.

Как учим?

Итак, нам нужно выучить сетку восстанавливать картинку из шума. Нужен обратный процесс. Необходимо его выучить. Допустим, у нас есть некоторая вероятностная модель с ненаблюдаемыми переменными (латентными переменными, латентное пространство) z и наблюдаемыми переменными x. Наша цель - на основе наблюдаемых данных x научиться оценивать распределение латентных переменных z, чтобы можно было делать выводы о них.Однако в большинстве случаев точное вычисление этого распределения невозможно или слишком сложно. Вот где приходит вариационный вывод, и его идея заключается в том, чтобы приближенно оценить распределение латентных переменных z, используя другое, проще распределение q(z|φ), параметризованное некоторыми параметрами φ.

ELBO - это функция, которая помогает нам приближенно оптимизировать параметры φ так, чтобы получить наилучшую аппроксимацию для истинного распределения латентных переменных p(z|x). ELBO можно записать следующим образом:

где E[log p(x|z)] - математическое ожидание логарифма правдоподобия наблюдаемых данных x при условии латентных переменных z, и KL(q(z|φ) || p(z)) - расстояние Кульбака-Лейблера между приближенным распределением q(z|φ) и истинным апостериорным распределением p(z|x).

Минимизируя расстояние Кульбака-Лейблера, то есть приближая наше другое распределения к истиному, мы таким образом максимизируем ELBO.

$\begin{aligned} L_t &= \mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}} \Big[\frac{1}{2 \| \boldsymbol{\Sigma}_\theta(\mathbf{x}_t, t) \|^2_2} \| {\tilde{\boldsymbol{\mu}}_t(\mathbf{x}_t, \mathbf{x}_0)} - {\boldsymbol{\mu}_\theta(\mathbf{x}_t, t)} \|^2 \Big] \\ \end{aligned}$

Зачем делить на матрицу ковариции? Для нормализации. В данном контексте ковариация представляет структуру изменчивости данных и определяет, насколько переменные данных связаны друг с другом.

Формула для значение среднего полученных от модели данных у нас есть, формулу для среднего наблюдаемых данных мы знаем. Подставляем в формулу и после некоторых преобразований получаем:

$\begin{aligned} L_t &= \mathbb{E} \Big[\|\boldsymbol{\epsilon}_t - \boldsymbol{\epsilon}_\theta(\sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t, t)\|^2 \Big] \end{aligned}$

По факту сетка пытается выучить предсказывать шум. В итоге лосс получается такой:
Шум - шум, который предсказывает сетка.

Конец

Про диффузионные модели можно много чего сказать, но статья получилась довольно объемная и устрашающая своими математическими формулами. Поэтому разумно разделить ее на несколько частей.

Помимо голой теорий мне бы хотелось выделить в отдельную статью практический пример генеративной модели, а также разновидности моделей, применение, методы ускорения.

Благодарю за внимание!