03.01.2024 16:05
ABy 53 15000 Источник

В 1982 годy американские студенты, сдававшие SAT тест (аналог ЕГ) должны были ответить на простой вопрос. Звучал он следующим образом:

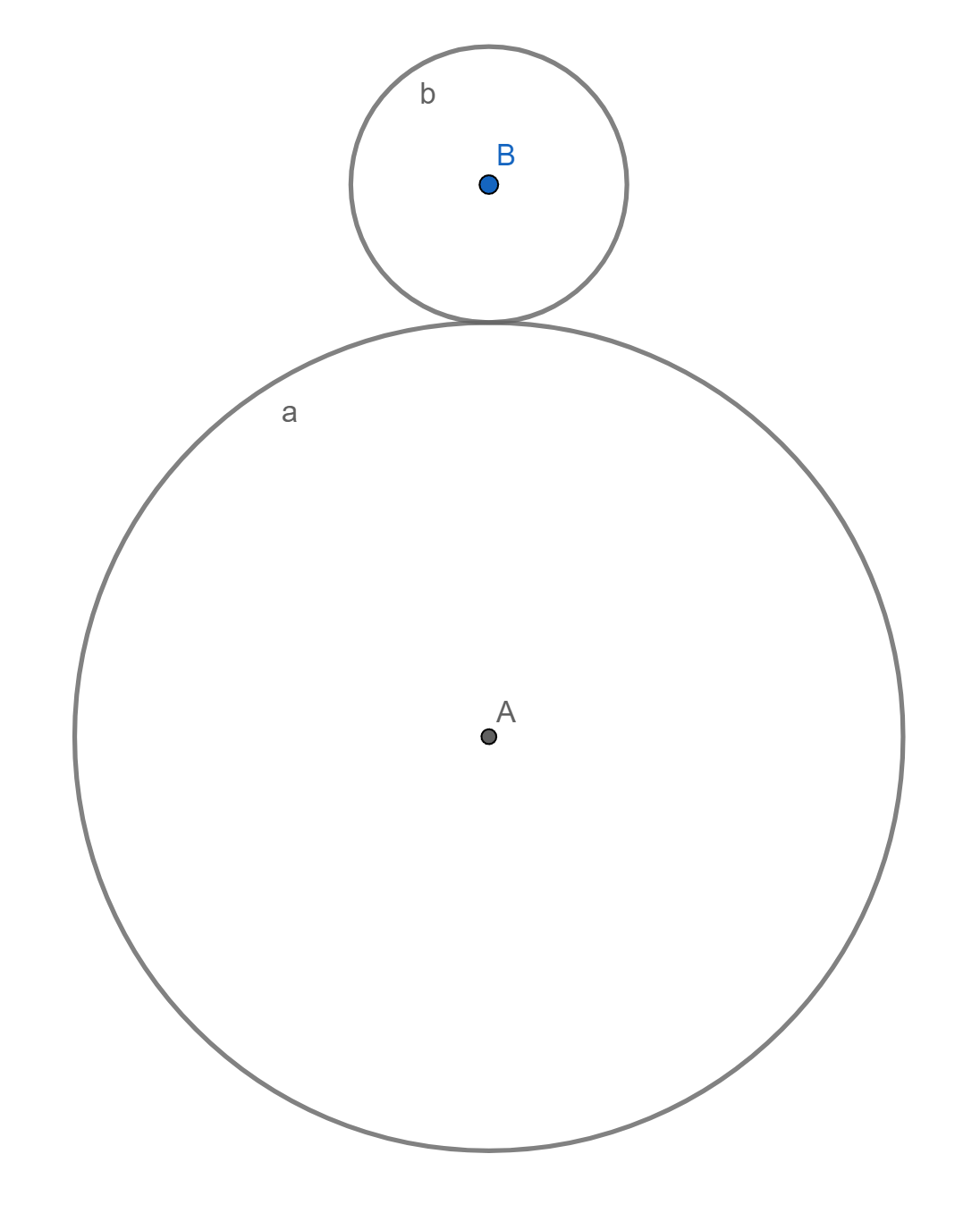
Радиус окружности a в три раза больше чем радиус окружности b. Начиная с позиции, показанной на изображении, окружность b катится вокруг окружности a. К моменту когда окружность b вернется в начальную позицию, как много оборотов она совершит?
Варианты ответов:
а) 3/2
b) 3
c) 6
d) 9/2
e) 9

Вы ведь уже догадались что вопрос с подвохом? Тогда внимательно следите за движением точки H' и считайте обороты!

Итак, если вы выбрали вариант "b) 3" то сейчас я вам докажу что вы ошиблись. А если вы решили схитрить и выбрали вариант "a) 3/2", "c) 6", "d) 9/2" или "e) 9" то вы все равно ошиблись!

Давайте проследим за траекторией центра окружности b - точкой B. Она представляет собой окружность с радиусом:

R_c=R_a+R_b=4R_b

В таком случает длина траектории точки B это:

L_c =2\pi R_c= 2\pi(4R_b)=4(2 \pi R_b)=4L_b

Получается что нужно 4 оборота окружности b чтобы точка B вернулась в свое первоначальное положение!

Так чему вы же больше верите: своим глазам или математическим расчетам?

Тогда попробуйте посчитать количество оборотов еще раз. На этот раз я добавил на рисунок оси, привязав их к центру окружности b, чтобы вам было проще.

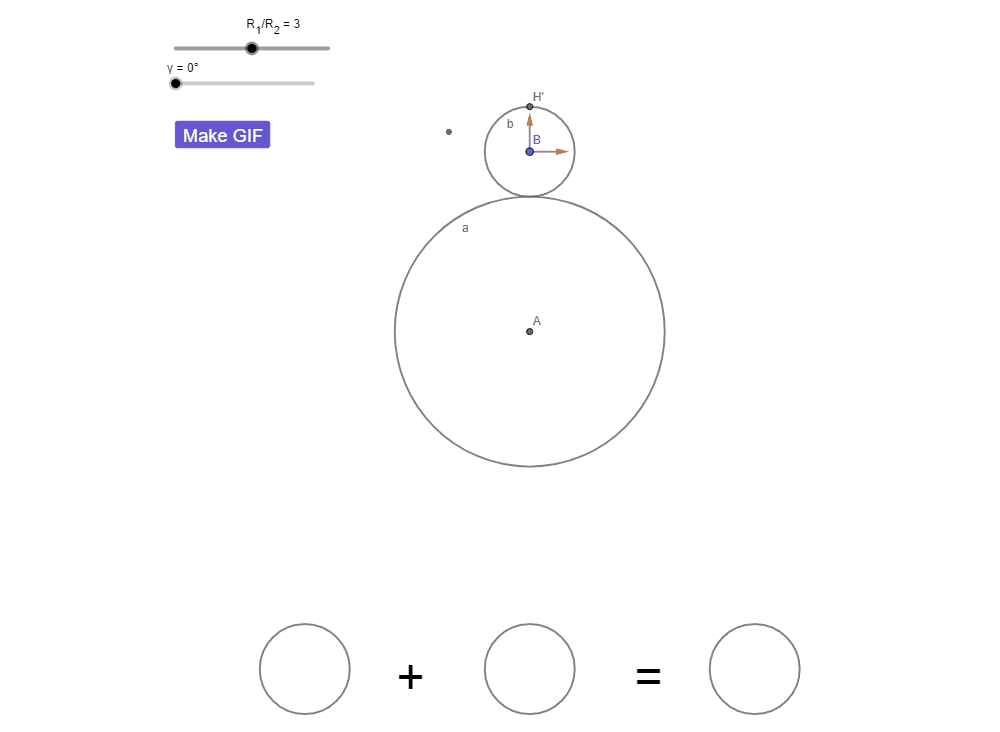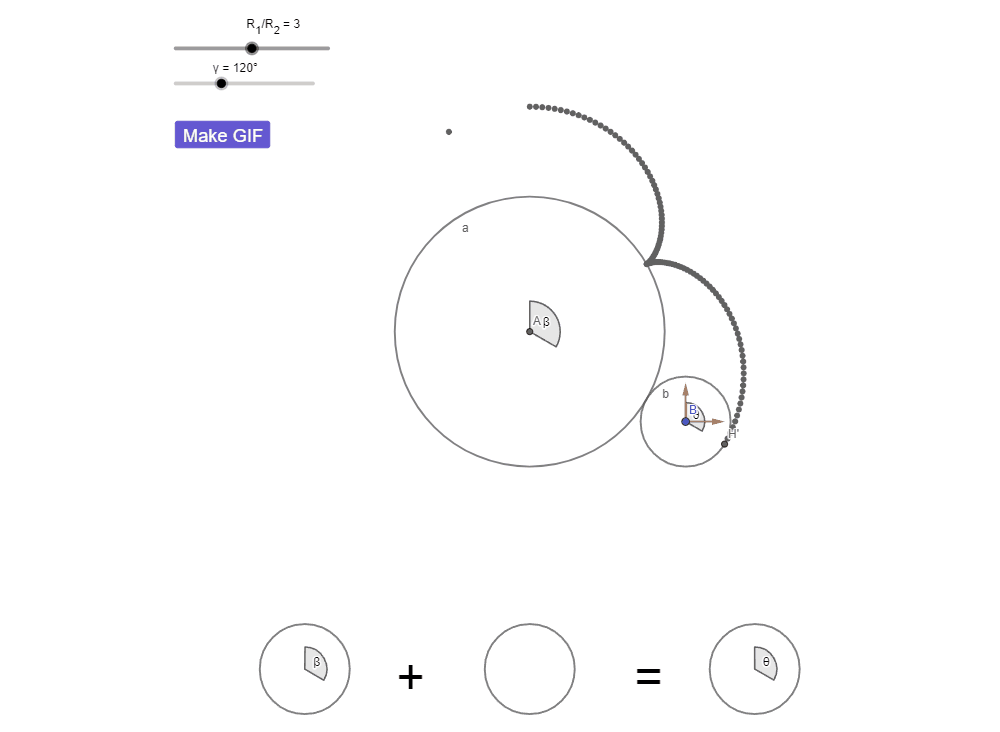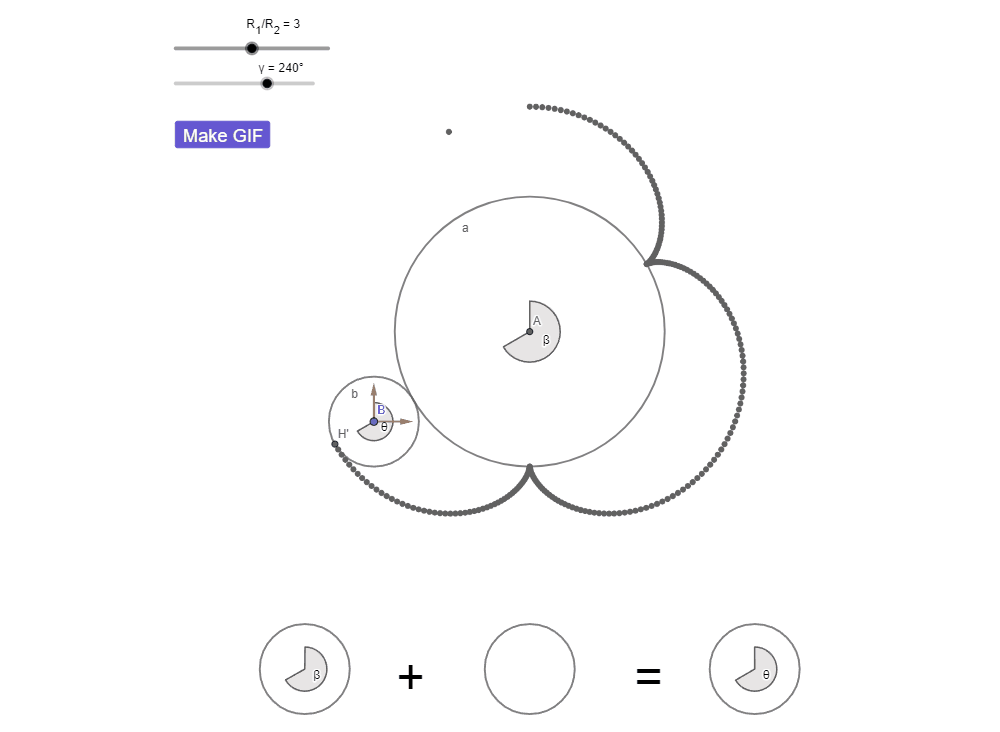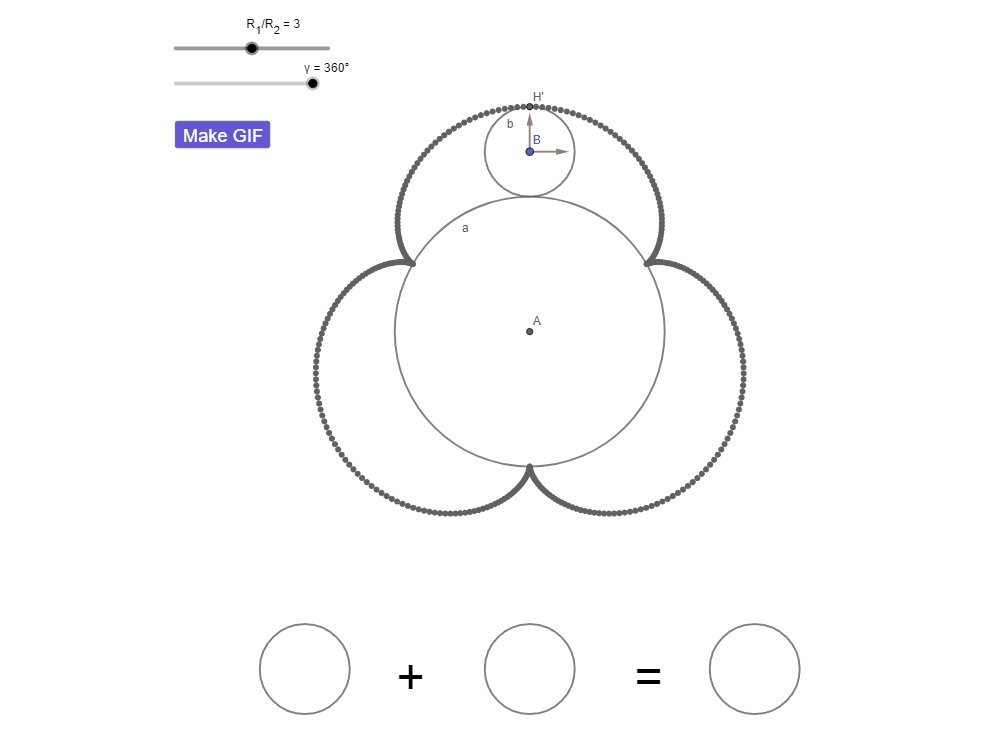
На рисунке β - угол поворота окружности с относительно точки А, ζ - угол поворота точки на окружности H' относительно центра окружности В, θ - сумма этих углов
На рисунке β - угол поворота окружности с относительно точки А, ζ - угол поворота точки на окружности H' относительно центра окружности В, θ - сумма этих углов

Думаю теперь вам не составило труда увидеть все 4 оборота.

Давайте проделаем тот же трюк, но со знакомыми нам предметами материального мира.

Положим на стол две одинаковые монеты так, чтобы они касались друг друга. Держа одну монету неподвижно, начнем вращать вокруг нее другую, избегая проскальзывания в точке соприкосновения монет - нам помогут насечки на ребрах. Заметим что к моменту когда монета достигнет противоположной стороны неподвижной монеты, она совершит один полный оборот. Продолжая вращать монету вернем ее в первоначальную позицию и отметим, что монета совершила еще один полный оборот. Парадоксальным образом монета прошла расстояние вдвое превышающее длину окружности второй монеты!

Проиллюстрируем вращение монеты с помощью геометрических построений.

Так в чем же секрет?!

Как и для любого хорошего фокуса, секрет в том, чтобы отвлечь внимание зрителя. Есть такой незамысловатый трюк, когда фокусник подбрасывает монету, делает вид что ловит ее правой рукой, но рука проходит немного выше и он ловит воздух, а монета падает в его левую руку. И пока зрители продолжают следить за правой рукой, думая что в ней монета, фокусник опускает монету в карман, затем раскрывает ладонь и показывает всем что монета исчезла.

Давайте возьмем две окружности с одинаковыми радиусами и пускай вместо того чтобы катиться, окружность b скользит по окружности a. Следите за точкой H.

Как видите, окружность совершает оборот, хоть и не вращается вокруг своего центра B.

Вернемся к задаче из теста и проделаем то же самое. Пускай окружность b просто скользит!

Надеюсь что теперь вы увидели "пропавший" оборот. Достаточно было внимательно наблюдать за тем, от чего вас отвлекли, чтобы разгадать секрет. Ведь этот дополнительный оборот - это оборот самой окружности b вокруг точки A!

Если вас заинтересовала статья и вы хотите узнать больше, советую посмотреть видео на канале Veritasium под названием The SAT Question Everyone Got Wrong. В нем намного подробнее рассказывается тема этой статьи.

Также можете взглянуть на статью в википедии Coin rotation paradox

Комментарии (53)


  1. vitslepukhin
    04.01.2024 13:01
    #0
    +3

    Спасибо за дружелюбный тон!! Дерзил, был не прав, однако ожидал более академичного ответа.
    Открыв учебник теормеха еще раз, можно сообразить немного побольше.
    Да, действительно b повернется вокруг B 4 раза.
    Применил тот же подход, разделяя поступательное движение и вращение. При внимательном рассмотрении вращательного движения окажется, что b совершает сложное вращение - относительно B и относительно A. И угол поворота окружности b можно описать формулой
    φ = 2π(1+\frac{R_{A}}{R_{B}})

    Рис. 1
    Рис. 1

    На рис. 1 показано качение круглого тела OB по окружности радиусом Ra из положения OB в положение O`B` за время t. За это время тело OB повернется вокруг A на угол ψ. И на угол ɛ вокруг B - его можно вычислить, зная, что OQ = O`Q, то есть .

    Общий поворот φ=ψ+ε=ψ+ψ\frac{R_{A}}{R_{B}}=ψ(1+\frac{R_{A}}{R_{B}})

    На рис. 1 показан масштаб задачи - Ra = 3, Rb = 1, ψ=π/4 - получаем φ=π.
    Для ψ=2π, получаем угол φ=4*2π - то есть 4 оборота.
    Для задачи с одинаковыми монетками - 2*2π.


  1. maximw
    04.01.2024 13:01
    #26335602
    +2

    К моменту когда окружность a вернется в начальную позицию, как много оборотов она совершит?

    Наверно, опечатка, имеется в виду откружность b?


    1. ABy Автор
      04.01.2024 13:01
      #26335616
      +2

      Да, опечатка. Спасибо! У меня уже "глаз запылился" чтобы самому такое отлавливать.


  1. maximw
    04.01.2024 13:01
    #26335690
    +6

    Мне кажется, фокус в том, что в статье есть бездоказательный переход в том месте, что длина траектории точки B кратна числу оборотов окружности b, примерно как хитрое извлечение корня в доказательстве, что 2 + 2 = 5. По-моему это неправильно. Ну и в конце путается процесс вращения и обращения (в терминах астрономии)


    1. ABy Автор
      04.01.2024 13:01
      #26335836
      +1

       есть бездоказательный переход в том месте, что длина траектории точки B кратна числу оборотов окружности b

      Да, есть такое:) Не хотелось на этом акцентироваться, поскольку мне это утверждение казалось довольно интуитивным. По ссылке это более подробно объясняется. Лучше чем у меня могло бы получиться.


    1. ABy Автор
      04.01.2024 13:01
      #26335992
      +2

      В принципе, мы можем проследить траекторию движения не центра окружности b, а точки H' лежащей на окружности. Пускай радиус окружности b равен r. В таком случае для вращения окружности b вокруг окружности a с равным радиусом, траектория точки будет представлять собой кардиоиду длиной 16r, а для движения по прямой циклоиду длиной 8r.


  1. nonickname227
    04.01.2024 13:01
    #26335964
    +5

    Очевидно, отношение длин плюс 1 оборот, т.к. траектория сама по себе является окружностью. Коварство в том, что среди предложенных ответов нет правильного, а ближайший - это 9/2, который совсем не правильный. Это что, на егэ бывают такие тесты?


    1. dyadyaSerezha
      04.01.2024 13:01
      #26337196
      +3

      Тоже не понял - коварства и отсутствия правильного ответа.


    1. MihaOo
      04.01.2024 13:01
      #26338572

      Если не ошибаюсь, то это пример из каких-то тестов в США, которые проводились в середине прошлого века или около того. С месяц назад попадал на видео на эту тему.


    1. Nakti
      04.01.2024 13:01
      #26338658

      Этому в видео уделили много времени, но тут опущено. Это был аналог ЕГЭ в США, и пришлось аннулировать этот вопрос (и пересчитать все баллы) после нескольких писем от проходивших. Автор вопроса решил, что правильным ответом было 3.


  1. santjagocorkez
    04.01.2024 13:01
    #26335994
    +28

    Нет никакого фокуса. Оборот — термин, подразумевающий точку отсчёта. Добавляя оборот вокруг центра большой окружности "фокусник" мошенничает, смешивая две системы координат. Поэтому ответ 3 будет корректным, а при отбраковке такого ответа на апелляции студенту достаточно указать, что точка отсчёта в задаче не указана, поэтому студент выбрал наиболее естественную для смысла задачи систему, имеющую центр малой окружности в качестве точки отсчёта. И в этой системе количество оборотов равно трём.

    Это как если бы в эйнштейновских системах за точку отсчёта выбрать точку "середина расстояния между точкой старта и текущим положением объекта" и таким образом доказать, что и объект, и точка старта равно ускоряются, а, следовательно, разницы скорости хода локального времени у них нет, как и не существует парадокса близнецов.


    1. ABy Автор
      04.01.2024 13:01
      #26336094
      -1

      Такой подход тоже имеет место быть.


      1. santjagocorkez
        04.01.2024 13:01
        #26337036
        +2

        По ссылке объясняют деталями терминологии, мол, есть несколько определений слова revolution (вращение). В задаче не сказано о сумме итераций по всем возможным определениям, следовательно, как я и говорил, студент вправе выбрать одно любое и предъявить ответ, соответствующий исключительно этому определению. Предложенные варианты, впрочем, недвусмысленно намекают на одно конкретное определение, которое подразумевали составители вопроса, и это то же самое, которое приходит на ум самым первым при прочтении.


  1. mikegordan
    04.01.2024 13:01
    #26336008
    +1

    не очень понял результат. я сейчас взял два круга от детской игры гольф, где один круг в 3 раза больше другого, на них нарисованы животные. Начал вращать руками как на картинке 1, у меня получилось ровно 3 оборота.


    1. ABy Автор
      04.01.2024 13:01
      #26336072
      +1

      Скорее всего вращали с проскальзыванием. Должно получиться как на видео.


      1. saboteur_kiev
        04.01.2024 13:01
        #26337676
        +6

        Весь "фокус" в неправильной или недостаточной формулировке. И все.


  1. Asaphalandor
    04.01.2024 13:01
    #26336580
    +6

    По определению - один полный оборот окружности соответствует углу в 360°. Вращение окружности B вокруг окружности A в определение оборота не попадает, таким образом правильный ответ 3.

    Возможно, в английском языке другие определения, и там этот фокус работает, в русском - нет.


  1. adeshere
    04.01.2024 13:01
    #26336584
    +1

    Кто читал «Вокру́г све́та за во́семьдесят дней», правильный ответ очевиден ;-)

    Но я не сразу сообразил, что "подвох" - именно в его отсутствии среди предложенных. Даже на какой-то момент усомнился: а не ошибся ли я?

    студенты, сдававшие SAT тест

    Так все-таки, откройте главный секрет: у студентов на тестировании тоже не было правильного ответа?


    1. ABy Автор
      04.01.2024 13:01
      #26336600
      +4

      Верно. Ошиблись составители теста. Трое студентов сообщили им об ошибке. В итоге всем прошедшим тест накинули баллы за этот вопрос как за правильный, не зависимо от их ответа.


      1. adeshere
        04.01.2024 13:01
        #26336630

        Трое студентов сообщили им об ошибке.... всем прошедшим тест накинули баллы за этот вопрос

        Несправедливо... Я бы этим троим дал дополнительный балл...


        1. ABy Автор
          04.01.2024 13:01
          #26336698
          +3

          Точно знаю что один из тех трех студентов набрал максимальный балл из из возможных.


          1. VPryadchenko
            04.01.2024 13:01
            #26336994

            И этими студентом был...


            1. Fell-x27
              04.01.2024 13:01
              #26337378
              +1

              ... Альберт Эйнштейн.


            1. alan008
              04.01.2024 13:01
              #26337528
              +1

              Александр Друзь


            1. kay_kay
              04.01.2024 13:01
              #26338856

              Сын председателя комиссии по сдаче SAT


  1. Vsevo10d
    04.01.2024 13:01
    #26336700
    +3

    Ну хоть Веритасиума самого процитировали, а не контентососов из Верт Дайдер.


    1. Nurked
      04.01.2024 13:01
      #26337160
      +2

      Я читаю и думаю "а что, так можно было?"

      Смотрел оригинал Веритассиума. Когда начал читать статью, подумал, наверняка перевод. Но нет, автор не указывает оригинал и не ставит перевод.

      Статья один-в-один повторяет видео. Но, что самое интересное, видео приложено.

      Я хотел пойти поругаться в комменты, что автор - тырит контент и нагоняет людей к себе в телеграмчик, но с удивлением НЕ обнаружил телеграм-канала.

      Это что вообще? Это мы так обленились, или это я чего то недопонял.


      1. smrl
        04.01.2024 13:01
        #26337578

        Люди, дорогие! Я тоже очень люблю Веритасиума, но свет клином на нем не сошелся. Тема боянистая, и в том же ютубе раньше (и куда глубже!) ну вот хотя бы тут было:
        https://youtu.be/oEN0o9ZGmOM?si=aU22enc9xZs51n8C&t=526


      1. ABy Автор
        04.01.2024 13:01
        #26337714

        Статья один-в-один повторяет видео.

        Стоп, а как же КДПВ?! Я же старался!


        1. Nurked
          04.01.2024 13:01
          #26338002

          Это вы честно признаётесь в плагиате?


          1. ABy Автор
            04.01.2024 13:01
            #26338038
            +1

            Ткните носом где именно вы видите плагиат. Мне даже интересно стало.


  1. DobrynyaPopovich
    04.01.2024 13:01
    #26336840
    +2

    Можно объяснить ответ так: 3 оборота получается за счёт того, что монета катится, прибавляем к этому один оборот за счёт того, что в добавок к качению монета как бы вращается за счёт движения по окружности


  1. Andy_U
    04.01.2024 13:01
    #26336996
    +3

    Вот оно, следствие исчезновения предмета "астрономия" из школьной программы. Ну ведь та же фигня с разницей длительности звездного и солнечного года в одни сутки :)


    1. ready4wisdom
      04.01.2024 13:01
      #26338474
      +3

      Нет, звездный (сидерический) и солнечный (тропический) не отличаются на сутки и то отличие, которое между ними есть обусловлено причинами не из темы данной заметки. Скорей всего имелось ввиду разница между числом суток в году и числом оборотов Земли вокруг оси, вот тут отличие в 1 как раз по теме данной заметки.


      1. Andy_U
        04.01.2024 13:01
        #26339002

        Да, согласен, вы правы.


  1. sena
    04.01.2024 13:01
    #26337040
    +2

    Задача с подвохом, формулировка нечёткая. Можно насчитать и 3 и 4 и 5
    оборотов, в зависимости от системы отсчёта и интерпретации, что такое
    'вращение'. Например если представить что мы живём на маленькой монете,
    как на планете, то мы увидим большую 3 раза. Если мы поместим
    наблюдателя в центр большой монеты и будем следить за маленькой,
    поворачиваясь за ней, то увидим одну точку 3 раза. Но при этом мы можем
    добавить ещё свой собственный оборот, то есть выйдет 4. Если система
    отсчёта связанна с наблюдателем неподвижным, то тогда 4 вокруг
    собственной оси, то есть 4 раза монета будет ориентирована одинаково
    относительно направления на север наблюдателя. Но есть ещё движение, оно
    тоже вращательное, вокруг большой монеты, тогда выходит 5.


  1. vitslepukhin
    04.01.2024 13:01
    #26337088
    +2

    Если взять учебник по теоретической механике, то можно прийти к таким соображениям:

    1. Окружность b катится по окружности a и, тем самым, совершает плоское движение (двигается не поступательно).

    2. При этом, движение b можно разложить на два движения - поступательное вместе с полюсом и вращательное вокруг полюса. Выберем полюсом B. Тогда b поступательно перемещается по траектории a (двигается поступательно по окружности - это не считается вращением и не совершается оборот) и вращается вокруг B.

    3. Особо стоит отметить, что направление и величина угла поворота не зависят от выбора полюса.

    4. Примем, что оборот - это вращение фигуры вокруг полюса на 2π рад. Следовательно нужно определить на какой угол повернулась окружность b вокруг B и поделить на 2π.

    5. Рассмотрим вращение b вокруг B. Так как b катится без проскальзывания по всей a один раз, то точки окружности b преодолели расстояние, равное длине окружности a. То есть повернулись вокруг B на угол 2π * Ra / Rb = 3*2π, а значит сделали 3 оборота.

    В статье и в видео указано, что длина окружности c Lc = 4*2π. Из чего делается вывод о том, что b повернется на 4 оборота. Но это не так, потому что B проходит расстояние Lc в поступательном движении и 0 при вращательном (если выбрать B за полюс, что удобно в этом случае). А вращение происходит на угол, такой, что точки окружности b, соприкасающиеся с окружностью a переместятся на расстояние La = 2π * Ra - следовательно вращение происходит на угол 2π * Ra / Rb.

    @ABy пожалуйста опровергните мой комментарий или свою статью.


    1. nonickname227
      04.01.2024 13:01
      #26337630

      Оборот - единица измерения угла. На какой угол повернется малая окружность?

      4\cdot 2\pi

      Сколько это оборотов? Это 4 оборота.

      Спасибо, пожалуйста


    1. ABy Автор
      04.01.2024 13:01
      #26337682

      Хороший комментарий. Спасибо что потратили время.

      Могу возразить что для меня не очевидно что "оборот" должен совершаться обязательно во вращательном движении. Из вики

      Оборот (цикл, круг, полный угол) — единица измерения угла, либо фазы колебаний.

      При измерении угла обычно используется название «оборот», а при измерении фазы — «цикл». Один оборот равен минимальному углу поворота, при котором положение (несимметричной) системы совпадает с первоначальным. Один цикл равен фазе, соответствующей времени в один период.

      Скажем у нас не две окружности, а два соприкасающихся квадрата. Один квадрат скользит по стороне другого. Когда он вернется в первоначальное положение, это будет считаться оборотом? Мы ведь можем провести из центра неподвижного квадрата прямую к центру движущегося и замерять угол поворота во время движения.

      Либо когда мяч отскакивает от пола. Когда он вернется в первоначальное положение - это можно назвать оборотом?

      Ну или в магазин за пивом сбегать и быстро "обернуться"


      1. nonickname227
        04.01.2024 13:01
        #26337748

        Зачем додумывать то, чего нет. Тело повернулось на угол 2пи в некоторой системе координат - оно совершило оборот. Ваш квадрат повернулся на 2пи? Если он скользил все время одной своей стороной, то повернулся, а значит совершил оборот. Мяч, если не крутился в воздухе, то оборот не совершил. А за пивом - скорее всего получится только пол оборота, потому что обычно для возвращения в исходную точку человеку нужно развернуться на 180 градусов )

        Если допридумывать разные условия, то получится что движущееся тело вообще вращаться не может. Это ж ужос какой-то и кошмар.


      1. ABy Автор
        04.01.2024 13:01
        #26338208

        Я тут ещё подумал, и скажем, в случае мяча, вектор его скорости будет совершать мгновенный оборот на 180° в момент соприкосновения с поверхностью и в верхней точке тракетории. По крайней мере возможна такая интерпретация.


        1. nonickname227
          04.01.2024 13:01
          #26338502

          Это неправильная интерпретация, потому что речь про вращение тела, а не вектора. Тело менять угол относительно пространства не будет.


      1. vitslepukhin
        04.01.2024 13:01
        #26338558
        +3

        Спасибо за дружелюбный тон!! Дерзил, был не прав, однако ожидал более академичного ответа.
        Открыв учебник теормеха еще раз, можно сообразить немного побольше.
        Да, действительно b повернется вокруг B 4 раза.
        Применил тот же подход, разделяя поступательное движение и вращение. При внимательном рассмотрении вращательного движения окажется, что b совершает сложное вращение - относительно B и относительно A. И угол поворота окружности b можно описать формулой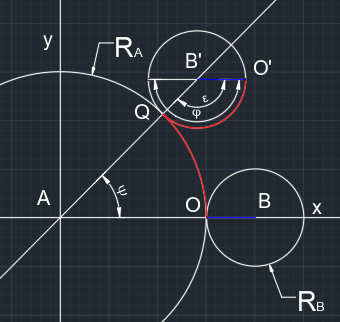
        φ = 2π(1+\frac{R_{A}}{R_{B}})

        Рис. 1
        Рис. 1

        На рис. 1 показано качение круглого тела OB по окружности радиусом Ra из положения OB в положение O`B` за время t. За это время тело OB повернется вокруг A на угол ψ. И на угол ɛ вокруг B - его можно вычислить, зная, что OQ = O`Q, то есть .

        Общий поворот φ=ψ+ε=ψ+ψ\frac{R_{A}}{R_{B}}=ψ(1+\frac{R_{A}}{R_{B}})

        На рис. 1 показан масштаб задачи - Ra = 3, Rb = 1, ψ=π/4 - получаем φ=π.
        Для ψ=2π, получаем угол φ=4*2π - то есть 4 оборота.
        Для задачи с одинаковыми монетками - 2*2π.


    1. ss-nopol
      04.01.2024 13:01
      #26338180
      +1

      двигается поступательно по окружности - это не считается вращением и не совершается оборот

      Это смотря как интерпретировать. Вокруг своей оси не совершает, но совершает оборот вокруг оси большой монеты. Земля ведь совершает оборот вокруг Солнца и плюс каждые сутки вокруг своей оси. Это два независимых вращения.

      Просто задача допускает интерпретации в силу нечёткой формулировки. И соответственно ответы от 3 до 5 включительно.


  1. riv9231
    04.01.2024 13:01
    #26337156
    +2

    Окружность - это математический объект, на котором нет ни вмятин, ни штрихов, по этому, он не может совершать обороты и в таких задачах должно отдельно оговариваться что и вокруг чего совершает обороты и в какой системе отсчета их счиатать. По моему, правильный ответ - один оборот. Но и 3 оборота тоже правильный ответ, кроме того если учитывать что малая окружность кроме "качения" ещё и совершает оборот вокруг большой окружности путем перемещения своего центра, то это можно трактаковать как 4 оборота. Все ответы верные в зависимости от того что описывает указанное построение из окружностей. Вот в этом и проблема ЕГЭ и подобных систем оценки "знаний".

    Составитель вопросов - "молодец", смог обмануть студентов, но что он узнал из их ответов?


  1. dmitry78
    04.01.2024 13:01
    #26337340

    по 2*π*r смотрим длины окружностей и кратны ли они целому числу - если да - у задачи есть решение, если нет - то шестерня провернется больше (меньше) чем на количество целых оборотов. Кстати, кожура больше апельсина.


  1. Tyusha
    04.01.2024 13:01
    #26337468
    +2

    Впору спросить уважаемую аудиторию: за какое время Земля совершает полный оборот вокруг своей оси? А потом удивляться правильному ответу 23:56.

    Затем можно было бы рассказать о разнице синодичечкого, сидерического и драконичечкого месяцев. А так заметка — детский сад какой-то.


  1. alexxz
    04.01.2024 13:01
    #26337530
    +1

    Все ж в задаче не указана ось вращения для подсчета. Вокруг оси малой окружности - 3 оборота. И это - самое очевидное предположение. Вокруг оси большой монеты - 1 оборот. Если вся система вращается вокруг чего-то, например, нарисована на грампластинке, то и еще могут быть обороты. Если катится достаточно долго, то стоит посчитать вращение всей системы вокруг оси вращения планеты и это тоже будет оборотами. Только все это - обороты вокруг разных осей вращения. И выбор оси вращения в центре малой окружности - нормальное допущение.


    1. ss-nopol
      04.01.2024 13:01
      #26338732

      Все ж в задаче не указана ось вращения для подсчета.

      Ни ось, ни система отсчёта.

      Вокруг оси малой окружности - 3 оборота.

      Это только в системе отсчёта (СО) направленной от центра малой монеты к большой. В неподвижной системе отсчёта - 4 оборота вокруг оси малой окружности, да плюс 1 вокруг вокруг оси большой монеты, то есть 5.


  1. SubbotinMaxim
    04.01.2024 13:01
    #26337688

    Можно ссылку на первоисточник задачи?

    Математика, математикой, но против логики не попрёшь.


    1. ABy Автор
      04.01.2024 13:01
      #26337692

      Есть в конце статьи.

      На организаторов теста ссылок у меня нет.


      1. LevPos
        04.01.2024 13:01
        #26340652

        В википедии есть ссылка на статью в The New York Times:

        ERROR FOUND IN S.A.T. QUESTION

        The disputed question shows a large circle, B, and to the left of it a small circle, A, touching B. ''In the figure above,'' the problem states, ''the radius of circle A is one-third the radius of circle B. Starting from position shown in figure, circle A rolls around circle B. At the end of how many revolutions of circle A will the center of circle A first reach its starting point?''


  1. Nail_S
    04.01.2024 13:01
    #26337842

    Я думаю тот тот же принцип что и в кругосветном путешествии. Смотря какую систему координат выберем получим различный результат.


  1. coxx
    04.01.2024 13:01
    #26340492
    -1

    Ничего не понял – слишком много уже комментариев.
    В оригинальном youtube-ролике речь идет про центр окружности A. Какого, простите, <специя>, автор перевода это слово упустил?