В этой статье мы разберемся, как в СУБД PostgreSQL реализован поиск страниц с необходимым свободным пространством для быстрой вставки записей в таблицу.

Для понимания статьи необходимо:

• Понимание основных механизмов работы PostgreSQL

• Базовое понимание языков Си и SQL

• Базовые навыки работы с терминалом на ОС Linux

Перед прочтением настоятельно рекомендую ознакомиться со статьей Егора Рогова: MVCC-2. Слои, файлы, страницы.

В этой статье мы разберемся:

• Что такое категории FSM страницы

• Как устроено дерево категорий на листовой FSM странице

• Как устроены нелистовые FSM страницы и дерево FSM страниц

• С чего начинается поиск свободного пространства в древовидной структуре FSM

• Как устроен алгоритм поиска нужной категории 

• Как устроен алгоритм обновления категорий

• Какие есть особенности работы FSM слоя для индексов

• При каких обстоятельствах FSM страницы блокируются 

• При каких обстоятельствах необходимо восстанавливать FSM страницы

• Когда FSM используется при вставке новых версий строк

Карта свободного пространства

Карта свободного пространства (free space map, FSM) - слой отношения, состоящий из FSM страниц, которые помогают быстро найти страницу из основного слоя для записи новой версии строки.  

FSM файлы, представляющие собой сегменты максимум по 1 гб, лежат вместе с файлами других слоев. Название FSM файла представляет собой oid таблицы и суффикс “_fsm”.

Чтобы обеспечить быстрый поиск свободного пространства, карта свободного пространства имеет древовидную структуру, состоящую минимум из трех уровней при стандартном размере страниц в 8 килобайт, и на каждый уровень для начала отводится по одной FSM странице. По мере необходимости дерево FSM страниц расширяется, неизменным остается только верхний уровень, соответствующий корневой странице FSM дерева. Каждая FSM страница также содержит внутри себя дерево, хранящее на своих узлах информацию о свободном пространстве страниц из основного слоя. 

Категории

Для начала рассмотрим самый нижний уровень иерархии карты свободного пространства - это категории.

Категория - это информация о свободном пространстве страницы из основного слоя конкретного отношения, на которую отведено по одному байту на каждую страницу. В один байт невозможно уместить точную информацию о количестве свободного пространства даже для страницы с минимальным возможным размером в 1 килобайт, поэтому категория описывает количество свободного пространства страниц из основного слоя в долях. Таким образом, в категорию можно уместить информацию о свободном пространстве с точностью до 1/256 страницы, а объем свободного пространства, который может иметь страница, разделен на 256 категорий. Наивысшая категория - 255, соответствует полностью свободной странице. Наименьшая категория - 0, соответствует несуществующей либо полностью заполненной странице.

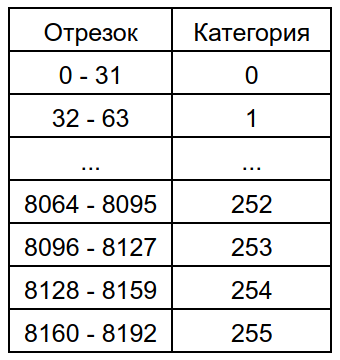
Каждая категория соответствует конкретному отрезку байтов. Наивысшая категория соответствует отрезку [MaxFSMRequestSize; BLCKSZ], следующая, 254-ая категория соответствует отрезку [254 * FSM_CAT_STEP; MaxFSMRequestSize - 1], 253 категория - [253 * FSM_CAT_STEP, 254 * FSM_CAT_STEP - 1] и так далее. Нулевая же категория соответствует отрезку [0, FSM_CAT_STEP - 1]. 

FSM_CAT_STEP - размер страницы, разделенный на количество категорий. 

#define FSM_CAT_STEP    (BLCKSZ / FSM_CATEGORIES)
#define FSM_CATEGORIES    256

По умолчанию BLCKSZ равен 8192 байтам, следовательно FSM_CAT_STEP будет равен 32. MaxFSMRequestSize равен максимальному размеру версии строки, которую можно уместить на странице, если закрыть глаза на TOAST. При стандартных конфигурационных параметрах MaxFSMRequestSize равен 8160 байтам.

#define MaxFSMRequestSize    MaxHeapTupleSize
#define MaxHeapTupleSize  (BLCKSZ - MAXALIGN(SizeOfPageHeaderData + sizeof(ItemIdData)))

MAXALIGN выравнивает количество байт до значения, кратного восьми.

Отрезки байтов, соответствующие категориям, будут выглядеть следующим образом.

Теперь рассмотрим на практике, как работают категории. Для этого воспользуемся расширением pageinspect, которое позволит нам заглянуть внутрь FSM страницы.

CREATE EXTENSION pageinspect;

Создаем таблицу test с одним integer столбцом.

CREATE TABLE test (a integer);

Перед вставкой разберемся с размером вставляемых строк. Каждая строка будет занимать 32 байта, а также 4 байта на указатель для версии строки, находящийся сразу после заголовка страницы. На заголовок версии строки отводится 24 байта (при 4х-байтном счетчике транзакций), после заголовка идет integer на 4 байта, итого выходит 28 байт. Также необходимо выровнять версию строки до значения, кратного восьми, итого выходит 32 байта, а с учетом указателя - 36 байтов. 

Вставим в таблицу одну запись и спровоцируем инициализацию карты свободного пространства для данной таблицы с помощью VACUUM.

INSERT INTO test VALUES (1);
VACUUM test;

Посмотрим категорию страницы, в которую была вставлена строка.

SELECT fsm_page_contents(get_raw_page('test1',  'fsm', 2));
 fsm_page_contents
-------------------
 0: 254       	+
 1: 254       	+
 3: 254       	+
 7: 254       	+
 15: 254      	+
 31: 254      	+
 63: 254      	+
 127: 254     	+
 255: 254     	+
 511: 254     	+
 1023: 254    	+
 2047: 254    	+
 4095: 254    	+
 fp_next_slot: 0  +

Пока не будем вдаваться в подробности. Все, что нас сейчас интересует, это предпоследняя строка, содержащая информацию о категории нашей единственной страницы из основного слоя, созданной при вставке.

Как мы видим, категория равна 254, иными словами, размер свободного пространства страницы входит в отрезок [8128; 8159].

SELECT (upper - lower) as free_space FROM page_header(get_raw_page('test1', 'main',0));
 free_space
------------
   	8132

Попробуем вставить еще одну строку.

INSERT INTO test1 VALUES (1);
VACUUM test1;
SELECT * FROM fsm_page_contents(get_raw_page('test1', 'fsm',2));
 fsm_page_contents
-------------------
 0: 252       	+
 1: 252       	+
 3: 252       	+
 7: 252       	+
 15: 252      	+
 31: 252      	+
 63: 252      	+
 127: 252     	+
 255: 252     	+
 511: 252     	+
 1023: 252    	+
 2047: 252    	+
 4095: 252    	+
 fp_next_slot: 0  +
SELECT (upper - lower) as free_space FROM page_header(get_raw_page('test1', 'main',0));
 free_space
------------
   	8096

8096 входит в отрезок [8096; 8127], соответствующий категории 253, а не 252, но как же так вышло? Дело в том, что функция, подсчитывающая категорию, использует количество свободного пространства на странице, из которого предварительно вычли размер указателя на новую версию строки, которую в любом случае нужно будет записать при следующей вставке. Таким образом, из значения 8096 нужно вычесть еще и размер указателя на следующую вставляемую версию строки равный 4 байтам. 8096 - 4 = 8092 уже входит в промежуток [8064; 8095], соответствующий 252-ой категории.

Структура FSM страницы

С категориями разобрались, теперь рассмотрим структуру листовой FSM страницы, включающую в себя дерево категорий. Листовые страницы находятся на нижнем уровне дерева FSM страниц. 

Структура данных FSM страницы (src/include/storage/fsm_internals.h)

typedef struct
{
    int   		 fp_next_slot;
    uint8   	 fp_nodes[FLEXIBLE_ARRAY_MEMBER];
} FSMPageData;

fp_next_slot

fp_next_slot - указатель на слот, с которого начинается поиск свободного места на FSM странице, чтобы каждый раз не начинать поиск с корневого узла. О нем поговорим чуть позже. 

fp_nodes   

fp_nodes содержит двоичное дерево категорий, хранящееся в массиве, где первые NonLeafNodesPerPage элементов соответствуют нелистовым узлам, а следом идут LeafNodesPerPage листовых узлов.

#define NonLeafNodesPerPage (BLCKSZ / 2 - 1)
#define LeafNodesPerPage (NodesPerPage - NonLeafNodesPerPage)
#define NodesPerPage (BLCKSZ - MAXALIGN(SizeOfPageHeaderData) - offsetof(FSMPageData, fp_nodes))

Таким образом, если заменить категории страниц на цифры, обозначающие позиции каждого узла в массиве, дерево будет выглядеть так:

В массиве узлы дерева будут расположены таким образом:

Нелистовые узлы дерева внутри FSM страницы устроены особым образом: они хранят максимальную из двух дочерних узлов категорию. Листовые узлы хранят категории, соответствующие страницам из основного слоя, но только на листовых FSM страницах.

Пример:

Таким образом, чтобы обнаружить, есть ли на fsm странице необходимая категория, достаточно посмотреть на корневой узел дерева.

Теперь, имея представление о структуре FSM страницы, мы можем понять вывод функции fsm_page_contents из расширеня pageinspect.

SELECT * FROM fsm_page_contents(get_raw_page('test1', 'fsm',2));
 fsm_page_contents
-------------------
 0: 252       	+
 1: 252       	+
 3: 252       	+
 7: 252       	+
 15: 252      	+
 31: 252      	+
 63: 252      	+
 127: 252     	+
 255: 252     	+
 511: 252     	+
 1023: 252    	+
 2047: 252    	+
 4095: 252    	+
 fp_next_slot: 0  +

Данная функция выводит информацию обо всех узлах на FSM странице, а именно пары, содержащие:

1. расположение узла в массиве

2. категорию 

Причем эта функция не выводит информацию об узлах с нулевой категорией. Также мы вывели информация именно о второй FSM странице, которая является листовой, в ней на листовых узлах находятся категории, соответствующие конкретным страницам из основного слоя. Нумерация страниц начинается с нуля, следовательно нулевая страница является корневой.

В данном случае дерево категорий выглядит следующим образом:

Если на одну версию строки будет отводиться по 36 байт, как в прошлом примере, то одна страничка сможет вместить 226 записей.

(8192 - 24)/ 36 = 226,(8) - округляем в меньшую сторону

Если мы вставим 226 записей, на странице не останется свободного пространства для вставки новой версии строки, так как останется всего 0.(8) * 36 = 32 байта свободного пространства. Не забываем, что FSM заранее учитывает еще и указатель на будущую вставляемую версию строки. Таким образом, категория будет соответствовать 28 байтам свободного пространства, то есть нулевой категории. Проверим, так ли это. Мы уже вставили в нашу таблицу 2 строки, вставим еще 224:

INSERT INTO test SELECT 1 FROM generate_series(1,224);
VACUUM test;

SELECT * FROM fsm_page_contents(get_raw_page('test', 'fsm',2));
 fsm_page_contents
-------------------
 fp_next_slot: 0  +

SELECT (upper - lower) as free_space FROM page_header(get_raw_page('test', 'main',0));
 free_space
------------
     	32

Количество свободного пространства, если не вычитать размер указателя, действительно равно 32 байтам. С учетом указателя количество свободного пространства равно 28 байтам, что соответствует нулевой категории, как и предполагалось.

Все узлы дерева после нашей вставки имеют нулевую категорию. Если мы вставим еще одну запись в таблицу, появится новая страничка в основном слое и соответствующая ненулевая категория на FSM странице.

INSERT INTO test VALUES (1);
VACUUM test;

SELECT * FROM fsm_page_contents(get_raw_page('test', 'fsm',2));
 fsm_page_contents
-------------------
 0: 254       	+
 1: 254       	+
 3: 254       	+
 7: 254       	+
 15: 254      	+
 31: 254      	+
 63: 254      	+
 127: 254     	+
 255: 254     	+
 511: 254     	+
 1023: 254    	+
 2047: 254    	+
 4096: 254    	+
 fp_next_slot: 0  +

Обновленное дерево:

неидеальность дерева категорий

По умолчанию размер одной FSM страницы равен 8192 байтам, а количество нелистовых узлов равно 8192/2 - 1 = 4095, следовательно количество листовых узлов должно быть равно 4096, но FSM странице нужно еще уместить fp_next_slot и заголовок страницы. Таким образом, на странице чисто физически не могут поместиться все 4096 листовых узла, поэтому двоичное дерево не идеально, и у него отсутствуют несколько крайних правых листовых узлов, а также есть несколько бесполезных нелистовых узлов.

Таким образом, схематично дерево выглядит таким образом:

где цифры обозначают позицию каждого узла в массиве. Расположение в массиве:

Устроим небольшой эксперимент, чтобы убедиться во всем этом.

Удалим старую тестовую таблицу и создадим новую.

DROP TABLE test;
CREATE TABLE test (a integer);

Для начала вычислим идентификатор крайнего узла в массиве на FSM странице, для этого из размера страницы вычтем размер fp_next_slot (4 байта), размер заголовка (24 байта) и еще 1 байт (так как индексация начинается с нуля). Таким образом, идентификатор крайнего узла в массиве равен 8192 - 4 - 24 - 1 = 8163, а всего листовых узлов 8192 - 4095 - 24 - 4  = 4069 штук.

Чтобы это проверить, вставим в нашу таблицу столько записей, чтобы дойти до 8163-го идентификатора узла. Для этого вставим 226 * 4068 + 1 записей, каждая из которых, как в прошлом примере, будет занимать по 36 байт. 

INSERT INTO test SELECT 1 FROM generate_series(1, 226 * 4068 + 1);
VACUUM test;

SELECT * FROM fsm_page_contents(get_raw_page('test', 'fsm', 2)) ;
 fsm_page_contents
-------------------
 0: 254       	+
 2: 254       	+
 6: 254       	+
 14: 254      	+
 30: 254      	+
 62: 254      	+
 126: 254     	+
 254: 254     	+
 509: 254     	+
 1019: 254    	+
 2040: 254    	+
 4081: 254    	+
 8163: 254    	+
 fp_next_slot: 0  +

Таким образом, мы дошли до последнего листового узла FSM страницы, а также записали одну версию строки на страницу из основного слоя, соответствующую последнему, 8163-ему, узлу. 

Проверим, правда ли данный узел последний. Для этого вставим еще 226 версий строк, чтобы перейти к следующему листовому узлу.

INSERT INTO test SELECT 1 FROM generate_series(1,226);
VACUUM test;

SELECT * FROM fsm_page_contents(get_raw_page('test', 'fsm',2)) ;
 fsm_page_contents
-------------------
 fp_next_slot: 0  +

Как и говорилось ранее, функция fsm_page_contents не выводит узлы с минимальной категорией, следовательно на второй FSM странице все категории равны нулю. 

Проверим, действительно ли создалась новая FSM страница. Выведем содержимое третьей FSM страницы. 

SELECT * FROM fsm_page_contents(get_raw_page('test', 'fsm',3)) ;
 fsm_page_contents
-------------------
 0: 254       	+
 1: 254       	+
 3: 254       	+
 7: 254       	+
 15: 254      	+
 31: 254      	+
 63: 254      	+
 127: 254     	+
 255: 254     	+
 511: 254     	+
 1023: 254    	+
 2047: 254    	+
 4095: 254    	+
 fp_next_slot: 0  +

Таким образом, дерево категорий действительно является неидеальным, у него отсутствует 4096 - 4069 = 27 правых листовых узлов.

Дерево FSM страниц

Мы уже рассмотрели категории и FSM страницы, теперь поднимемся еще на один уровень иерархии, который состоит из дерева FSM страниц. Нелистовые FSM страницы не сильно отличаются от листовых. Листовые узлы на страницах более высокого уровня соответствуют корневым узлам FSM страниц более низкого уровня, а не страницам из основного слоя. Корневой узел на каждой странице имеет то же значение, что и у соответствующего листового узла на родительской странице, если такова имеется. Схематично дерево FSM страниц выглядит так:

На иллюстрации листовые деревья имеют по два листовых узла на каждом дереве категорий. На самом же деле, как мы выяснили, листовых узлов 4069 штук.

Адрес FSM страницы представлен в структуре FSMAddress, хранящей уровень, на котором расположена страница FSM слоя, а также номер страницы на этом уровне.

typedef struct
{
    int   		 level;               / уровень FSM*/
    int   		 logpageno;   	 /* номер страницы внутри уровня*/
} FSMAddress;

Номера нижнего и корневого уровней FSM слоя соответственно.

#define FSM_BOTTOM_LEVEL 0
#define FSM_ROOT_LEVEL    (FSM_TREE_DEPTH - 1)	

#define FSM_TREE_DEPTH    ((SlotsPerFSMPage >= 1626) ? 3 : 4)

Например, если каждая страница FSM содержит информацию о 4 страницах, в FSM файлах страницы будут расположены в таком порядке:

Высота дерева FSM страниц

Дерево FSM слоя всегда имеет постоянную высоту. Чтобы охватить максимальный размер отношения в 2^32-1 страниц, хватит всего трех уровней, так как каждая FSM страница (при BLCKSZ = 8192) может хранить информацию о 4069 страницах. Таким образом, при двухуровневом FSM слое не поместится информация обо всех страницах отношения 4069^2 < 2^32, а при трехуровневом слое FSM места для категорий предостаточно, так как 4069^3 > 2^32. Поэтому FSM слой состоит минимум из трех страниц.

Также стоит отметить, что X = 1626 — это наименьшее значение, удовлетворяющее условию X^3 >= 2^32-1. В постгресе можно установить размер страниц, равный 1 или 2 килобайтам вместо 8, а это меньше чем 1626 * 2 байт. Для работы с малогабаритными страницами в FSM поддерживается и четырехуровневое дерево, чтобы поместилась информация о всех 2^32-1 страницах отношения.

Примечание: при конфигурации постгреса можно указать размер страниц:

./configure --with-blocksize=BLOCKSIZE

Доступные размеры: 1, 2, 4, 8, 16, 32 Кбайт

Устройство fp_next_slot

Древовидная структура карты свободного пространства позволяет реализовать алгоритм поиска нужной категории с логарифмической временной сложностью, но можно ускорить данный алгоритм, если начинать поиск не с корневого узла, а с какого-нибудь кэшированного узла, который был найден при последнем поиске. Именно для этого и нужен fp_next_slot, являющийся номером листового узла уровня на FSM странице, с которого начинается поиск новой страницы со свободным пространством. Рассмотрим на примере поведение этого вспомогательного указателя.

Создадим новую таблицу test. Заполним нулевую и первую страницы версиями строк, на вторую страницу запишем только одну версию строки, а также освободим место для двух строк на первой странице. Нумерация страниц основного слоя и категорий начинается с нуля.

DROP TABLE test;
CREATE TABLE test(a integer);
INSERT INTO test SELECT generate_series(1, 226 * 2 + 1);
DELETE FROM test WHERE a = 450;
DELETE FROM test WHERE a = 451;
VACUUM test;

Для удобства будем называть листовые узлы листовых FSM страниц слотами. Нумерация узлов начинается с корневого узла, поэтому первый листовой узел имеет номер 4095, что не очень удобно. Слоты же нумеруются начиная с листовых узлов.

Изначально указатель на следующий слот равен нулю. В нашем случае нулевой слот соответствует нулевой странице основного слоя.

SELECT * FROM fsm_page_contents(get_raw_page('test', 'fsm', 2));
 fsm_page_contents
-------------------
 0: 254       	+
.................
 4097: 254    	+
 fp_next_slot: 0  +

Вставим одну запись на первую страницу, в которой есть два вакантных места.

INSERT INTO test VALUES (1);

SELECT * FROM fsm_page_contents(get_raw_page('test', 'fsm', 2));
 fsm_page_contents
-------------------
 0: 254       	+
.................
 1023: 254    	+
 2047: 2      	+
 2048: 254    	+
 4096: 2      	+
 4097: 254    	+
 fp_next_slot: 2  +

Мы сделали вставку и для этого обратились к FSM. Во время поиска нужной категории указатель на следующий слот изменился, а информация о свободном пространстве первой страницы из основного слоя - нет. Таким образом, при изменении указателя на следующий слот страница блокируется не эксклюзивно. На данный момент указатель равен двум, что соответствует второй странице основного слоя. Можно подумать, что следующая вставка будет на вторую страницу, хоть и на первой еще осталось одно свободное место, но на самом деле при следующей вставке не будет искаться новая категория благодаря кэшу отношения, который сохранил последнюю найденную страницу. Указатель на следующий слот пригодится, когда при вставке новой записи не обнаружится необходимого свободного пространства в странице, номер которой находится в кэше.

INSERT INTO test VALUES (1); 

SELECT * FROM fsm_page_contents(get_raw_page('test', 'fsm', 2));
 fsm_page_contents
-------------------
 0: 254       	+
.................
 4097: 254    	+
 fp_next_slot: 2  +

При вставке еще одной строки указатель на следующий слот будет равен трем, так как первую страницу мы полностью заполнили, а на второй еще осталось много места, поэтому ее номер можно записать в кэш отношения, чтобы не обращаться лишний раз к карте свободного пространства. Как только место на второй странице закончится, указатель на следующий слот пригодится для поиска следующей страницы.

INSERT INTO test VALUES (1);

SELECT * FROM fsm_page_contents(get_raw_page('test', 'fsm', 2));
 fsm_page_contents
 -------------------
 0: 254       	+
.................
 4097: 254    	+
 fp_next_slot: 3  +

В нашем случае, если мы дальше будем вставлять версии строк, указатель на следующий слот не поменяется, так как карта свободного пространства вообще не будет использоваться. Версии строк будут просто последовательно записываться на новые страницы основного слоя. Карта свободного пространства будет считать, что свободного пространства не осталось.

INSERT INTO test SELECT generate_series(1, 452);

SELECT * FROM fsm_page_contents(get_raw_page('test', 'fsm', 2));
 fsm_page_contents
-------------------
 fp_next_slot: 3  +

После VACUUM указатель на следующий слот обнулится, чтобы можно было заново идти по листьям дерева с самого начала, так как VACUUM может удалить старые версии строк, вследствие чего появятся новые вакантные места и нам не придется создавать новые страницы для вставок новых версий строк.

VACUUM test;

SELECT * FROM fsm_page_contents(get_raw_page('test', 'fsm', 2));
 fsm_page_contents
-------------------
 0: 252       	+
 .................
 4099: 252    	+
 fp_next_slot: 0  +

С указателем на следующий слот на листовой FSM странице разобрались, но что происходит с указателем на нелистовой FSM странице?

Создадим новую таблицу и вставим столько версий строк, чтобы полностью использовать вторую FSM страницу и один слот на новой, третьей, странице.

DROP TABLE test;
CREATE TABLE test(a integer);
INSERT INTO test SELECT generate_series(1,226*4069 + 1);
DELETE FROM test WHERE a = 1;
VACUUM test;

Выведем содержимое первой FSM страницы. 

SELECT * FROM fsm_page_contents(get_raw_page('test', 'fsm', 1));

 fsm_page_contents
-------------------
 0: 254       	+
 .................
 2047: 254    	+
 4095: 1      	+
 4096: 254    	+
 fp_next_slot: 0  +

Если мы вставим еще одну строку, то полностью заполним вторую FSM страницу, а при последующей вставке нам уже нужно будет искать новую категорию.

INSERT INTO test VALUES (1);

SELECT * FROM fsm_page_contents(get_raw_page('test', 'fsm', 1));
 fsm_page_contents
-------------------
 0: 254       	+
.................
 2047: 254    	+
 4095: 1      	+
 4096: 254    	+
 fp_next_slot: 0  +

Мы использовали все слоты второй FSM страницы, следовательно, если мы сделаем еще одну вставку, указатель на следующий слот должен измениться. Можно сделать предположение, что указатель будет равен слоту, с которого начнется следующий поиск нужной категории, то есть будет равен двум, так как нулевая FSM страница будет заполнена, а первую FSM страницу мы будем использовать в данный момент. Проверим это:

INSERT INTO test VALUES (1);

SELECT * FROM fsm_page_contents(get_raw_page('test', 'fsm', 1));
 fsm_page_contents
-------------------
 0: 254       	+
 .................
 4096: 254    	+
 fp_next_slot: 1  +

Указатель на следующий слот теперь равен единице. Наше предположение оказалось неверным по одной простой причине: номера FSM страниц не кэшируются в отличие от номеров страниц основного слоя, в которых недавно была вставлена строка. Таким образом, fp_next_slot на нелистовых FSM страницах указывает на текущий слот, с которого и начнется поиск нужной категории.

Основные операции над FSM страницами

Для работы с картой свободного пространства на уровне конкретных FSM страниц используются две функции: поиск слота с необходимой категорией на странице (fsm_search_avail) и установка нового значения слота (fsm_set_avail).

fsm_search_avail

Поиск нужного слота одновременно использует и возможности древовидной структуры данных, и fp_next_slot, позволяющий искать слот не с корневого узла. 

Возьмем пример, где у дерева 8 листовых узлов, указатель на следующий слот (fp_next_slot) равен трем, а слот с необходимой категорией является пятым.

Поиск начнется с таргетированного узла, соответствующего указателю на следующий слот. Если последний поврежден, поиск начнется с нулевого слота. Красным пометим таргетированный узел.

Далее таргетированный узел поднимается на верхние узлы, являющиеся родителями для него и правого соседа, до тех пор, пока таргетированный узел не дойдет до узла с необходимой категорией, либо пока не обнаружит отсутствие правого соседа, что эквивалентно отсутствию нужной категории на дереве. Таргетированный узел может быть правым только в самом начале поиска, в данном случае необходимо просто подняться на родительский узел. Чем выше находится таргетированный узел, тем больше у него становится треугольник поиска, определяющий область видимости узлов. В треугольник поиска будут рекурсивно входить все дочерние узлы таргетированного узла. В нашем случае он дойдет до корневого узла, следовательно треугольник поиска будет размером с дерево категорий. Данный случай самый неблагоприятный, так как с большим успехом можно было просто начать поиск с корневого узла, но данный алгоритм рассчитан на то, что в большинстве случаев не нужно будет подниматься до корневого узла. Желтым цветом помечен треугольник поиска.

При подъеме наверх дерево поиска расширяется в два раза за шаг. На нижней иллюстрации было сделано два шага.

Как и говорилось ранее, при нахождении узла с нужной категории таргетированный узел перестанет подниматься.

Далее, после нахождения нужной категории, необходимо спуститься по дереву до подходящего листового узла

При спуске треугольник поиска сужается в два раза за каждый шаг. Сделаем еще два шага.

Таким образом данный алгоритм нашел узел с необходимой категорией.

И на листовых, и на нелистовых FSM страницах используется схожий механизм. 

fsm_set_avail

Данная функция обновляет категорию узла и перестраивает верхние узлы, чтобы восстановить нормальное состояние дерева.

Для примера снова возьмем дерево с 8 листовыми узлами и обновим категорию у второго слота с 2 на 4.

Для начала обновим категорию непосредственно у изменяемого слота. Обновленные узлы пометим красным.

Затем необходимо скорректировать изменения до верхних узлов, пересчитывая значение родительских узлов как максимальное из двух его дочерних элементов до тех пор, пока мы не дойдем до родительского узла, значение которого будет больше или равно новому значению нашего слота.

Подпрограммы более высокого уровня, использующие страницы FSM, получают к ним доступ через функции fsm_set_avail() и fsm_search_avail(), что позволяет рассматривать страницу FSM как черный ящик с определенным количеством слотов для хранения информации о свободном пространстве.

Работа с индексами

Работа с индексными страницами практически не отличается от работы с обычными страницами, но вместо отслеживания количества свободного места, отслеживается только то, использованы или свободны индексные страницы.

Например, данная функция помечает индексную страницу как полностью свободную:

void 
RecordFreeIndexPage(Relation rel, BlockNumber freeBlock)
{
    RecordPageWithFreeSpace(rel, freeBlock, BLCKSZ - 1);
}

Таким образом, свободной индексной странице соответствует слот на FSM странице с максимальной категорией. 

Если необходимо пометить индексную страницу как использованную, устанавливается 0 байт свободного пространства, что соответствует минимальной категории.

void
RecordUsedIndexPage(Relation rel, BlockNumber usedBlock)
{
    RecordPageWithFreeSpace(rel, usedBlock, 0)
}

БЛОКИРОВКИ

Карта свободного пространства является разделяемым ресурсом, следовательно она подвергается состоянию гонки, поэтому необходимо использовать механизм синхронизации. Хоть карта свободного пространства и является вспомогательным инструментом, при редактировании дерева категорий FSM страница блокируется эксклюзивно. Каждая FSM страница атомарна и является минимальной единицей данных, которую можно заблокировать, поэтому за один раз может блокироваться только одна страница -  блокировка родительской страницы освобождается перед блокировкой дочерней. Кроме дерева категорий на FSM странице есть еще и указатель на следующий слот, искажение которого не столь критично, поэтому при изменении fp_next_slot используется совместная блокировка.

Мы сможем убедиться в наличии эксклюзивной блокировки, если первый бэкенд решит изменить FSM страницу, которую уже изменяет другой бэкенд. Так как изменение дерева категорий происходит практически мгновенно, мы используем gdb отладчик, чтобы отловить момент эксклюзивной блокировки. 

Подробнее про отладку постгреса можно прочитать в статье Толмачева Павла.

Для начала запустим первый бэкенд, создадим таблицу и заполним под завязку одну страницу.

# Терминал №1
o4ina/home$ psql
postgres=# DROP test;
postgres=# CREATE TABLE test (a integer);
postgres=# INSERT INTO test SELECT generate_series(1, 226);
postgres=# VACUUM test;

Также нам необходим pid первого бэкенда, чтобы подключить к нему отладчик.

# Терминал №1
postgres=# SELECT pg_backend_pid();
 pg_backend_pid
----------------
      	25561

Далее запустим gdb в другом терминале, создадим точку останова в функции fsm_set_and_search, которая и должна заблокировать FSM страницу, и подключимся к бэкенду.

# Терминал №2
o4ina/home$ cd postgreSQL/bin
o4ina/home/postgreSQL/bin$ sudo gdb postgres
(gdb) b fsm_set_and_search
(gdb) attach 25561

Вставим одну строку в таблицу. Для нее не будет места на нашей единственной странице, поэтому необходимо обновить информацию об этой странице в FSM и получить новую для вставки.

# Терминал №1
postgres=# INSERT INTO test VALUES (1);

Далее выполним часть кода вплоть до эксклюзивной блокировки включительно.

# Терминал №2
(gdb) c
Continuing.
Breakpoint 1, fsm_set_and_search (rel=0x7d694d6ca058, addr=..., slot=0, newValue=0 '\000', minValue=1 '\001') at freespace.c:635
635   	 int   		 newslot = -1;
(gdb) n
637   	 buf = fsm_readbuf(rel, addr, true);
(gdb) n
638   	 LockBuffer(buf, BUFFER_LOCK_EXCLUSIVE);
(gdb) n

Теперь наша листовая FSM страница заблокирована.

Запустим в другом терминале второй бэкенд и попробуем вставить строку в таблицу.

# Терминал №3
o4ina/home$ psql
postgres=# INSERT INTO test VALUES (1);

Таким образом, второй бэкенд встал в очередь из-за эксклюзивной блокировки.

Как только первый бэкенд разблокирует FSM страницу, сразу в двух бэкендах пройдут операции вставки

# Терминал №2
(gdb) c

# Терминал №1
INSERT 0 1

# Терминал №3
INSERT 0 1

Эта эксклюзивная блокировка не критична, так как накладывается она только при обновлении FSM страницы. FSM страница обновляется при выполнении команды INSERT только в том случае, когда на странице из основного слоя закончилось место. Лишний раз не обновлять FSM нам позволяет кэширование номеров обычных страниц, в которые в последний раз были вставлены версии строк.

Указатель на следующий слот обновляется при поиске во время совместной блокировки, но, так как он является не более чем подсказкой для алгоритма поиска нужного слота, его повреждение не критично.

Восстановление

Восстановление данных после сбоя является важной частью СУБД, но так ли важна информация в FSM, чтобы записывать ее изменение в WAL? FSM играет второстепенную роль, и ее повреждение максимум приведет к менее эффективному поиску страниц со свободным пространством или чуть большему разбуханию таблицы, а при появлении искаженной информации на FSM страницах ее с легкостью можно восстановить.

Как мы знаем, если буферная страница была изменена, она помечается как “грязная”. Существует несколько видов таких меток:

1. MarkBufferDirty - информацию об изменении страницы необходимо в обязательном порядке записать в WAL.

2. MarkBufferDirtyHint - информацию об изменении страницы не нужно записывать в WAL.

При изменении FSM страницы ставится именно метка MarkBufferDirtyHint, следовательно информация об изменении FSM не попадает в WAL.

Страница нижнего уровня нуждается в перестройке при обнаружении определенных дефектов:

1. Если корневой узел FSM страницы меньше нового значения листового узла после пересчитывания нелистовых узлов при обновлении листового узла, то данная страница повреждена, так как категория корневого узла не может быть меньше листового узла на fms странице. 

2. Если для нелистового узла установлено слишком большое значение, данная страница также повреждена. Эта ошибка обнаруживается и исправляется при поиске слота с нужной категорией.

В обоих случаях обнаруженные дефектные узлы должны немедленно перестроиться.

Механизм получения буфера страницы со свободным пространством

Разберем на простых примерах, при каких обстоятельствах используется карта свободного пространства. Для этого рассмотрим механизм чтения буфера с необходимой страницей для записи новой версии строки. Данный функционал содержится в модуле hio.c, а рассматривать мы будем поведение только одной функции - RelationGetBufferForTuple(), так как именно она наиболее тесно связана с FSM.

Алгоритм работы функции RelationGetBufferForTuple

Сначала проверяется, есть ли в кэше номер прошлой таргетированной страницы (страницы, с которой работает алгоритм в данный момент), в которую мы последний раз вставляли версию строки. Для этого используются два кэша: 

1. Кэш отношения 

2. Список кэшированных номеров страниц под названием bistate (Bulk Insert State). В нем находятся номера лишних страниц, полученных при массовой вставке (в данной статье мы не будем рассматривать множественные вставки и, соответственно, работу данного кэша) 

Если бэкенду не удалось найти номер страницы в кэше отношения, необходимо найти номер страницы со свободным пространством с помощью карты свободного пространства (функция GetPageWithFreeSpace).

Если в FSM не нашлось страницы с необходимым свободным пространством, в номер таргетированной страницы записывается значение InvalidBlockNumber. При таких обстоятельствах необходимо еще проверить последнюю страницу в отношении на наличие свободного пространства. Это позволит избежать синдрома “одна версия строки на страницу”, когда у отношения еще пока нет FSM слоя, в кэше пусто, а в отношении уже есть страницы. В данной статье мы не будем рассматривать данный случай.

Далее начинается цикл, в который можно зайти только при удачном получении таргетированной страницы. Иными словами, номер таргетированной страницы не должен быть равен InvalidBlockNumber.

Каждая итерация цикла включает в себя:

1. чтение буфера таргетированной страницы и установку эксклюзивной блокировки буфера. 

2. Вычисление количества свободного пространства на прочитанной странице, даже если мы получили таргетированную страницу благодаря FSM. Данная проверка защищает от того, что на странице уже может и не быть необходимого свободного пространства, если какой-то бэкенд заполнил все вакантные места на странице во временном промежутке между получением номера таргетированной таблицы через FSM и эксклюзивной блокировкой таблицы. Также эта проверка необходима, если была прочитана последняя страница основного слоя (дабы избежать синдром “одна версия строки на страницу”), и при этом на ней все же не оказалось необходимого свободного пространства. 

3. Если таргетированная страница на самом деле имеет необходимое свободное пространство, записываем ее номер в кэш отношения и возвращаем буфер с этой страницей в вышестоящую функцию.

4. Если необходимого свободного пространства все же не оказалось, мы должны обновить информацию о ней в FSM и попытаться найти номер новой таргетированной страницы. 

5. Если номер новой таргетированной страницы не удалось найти, выходим из цикла, в ином случае начинаем новую итерацию.

Если мы вышли из цикла, это означает, что нам не удалось найти страницу со свободным пространством и необходимо создать новую. Также необходимо эту новую страницу записать в кэш отношения.

Упрощенная блок-схема данного алгоритма:

 

Теперь мы имеем представление об алгоритме получения буфера со страницей с необходимым свободным пространством. Рассмотрим пару примеров работы данного алгоритма.

Для начала, создадим таблицу и вставим туда записей ровно на две страницы, а затем освободим на первой странице место под одну запись, на второй - под две записи. Также не забываем про VACUUM, чтобы проинициализировать FSM.

CREATE TABLE test (a integer);
INSERT INTO test SELECT generate_series(1, 452);
DELETE FROM test WHERE a = 1;
DELETE FROM test WHERE a = 228;
DELETE FROM test WHERE a = 229;
VACUUM test;

Вставим одну строку в таблицу 

INSERT INTO test VALUES (1);

В начале бэкенд обратится к кэшу, чтобы получить номер возможно будущей таргетированной страницы, но попытка использования кеша не увенчается успехом, так как после VACUUM кэшированный номер страницы чистится. Следовательно, бэкенду необходимо найти в FSM номер страницы со свободным пространством.

Так как у нас в FSM есть информация о странице с необходимым свободным пространством - получаем номер страницы, заходим в цикл, читаем и эксклюзивно блокируем буфер таргетированной страницы, далее проверяем ее на наличие свободного пространства. Так как в нашей тестовой базе данных нет никаких других бэкендов, выполняющих вставки записей, на таргетированной странице все еще есть свободное место. Следовательно, бэкенду осталось только записать в кэш отношения номер таргетированной страницы и вернуть буфер страницы в вышестоящую функцию

Таким образом, мы вставили версию строки в единственное свободное место на первой страничке. Теперь попробуем сделать еще одну вставку в таблицу и посмотрим, как поведет себя алгоритм при наличии номера кэшированной страницы, не имеющей необходимого свободного пространства.

INSERT INTO test VALUES (1);

Сначала бэкенд пробует получить номер кэшированной страницы, в которую в последний раз была записана версия строки. На этот раз в кэше лежит номер предыдущей таргетированной страницы.

Страница из кэша не будет подходить, так как в ней нет необходимого свободного пространства, но узнает об этом алгоритм только после входа в цикл, чтения и блокировки буфера страницы. Раз уж таргетированная страница не подходит, необходимо записать информацию о ней в FSM и найти новую подходящую страницу, если такова имеется. В нашем случае осталась еще одна страница, в которую поместятся две версии строки, следовательно начнется новая итерация цикла, которая и вернет буфер с новой таргетированной страницей в вышестоящую функцию. 

Попробуем вставить еще одну строку в таблицу.

INSERT INTO test VALUES (1);

Данный случай является самым благоприятным, при котором бэкенду даже не нужно будет обращаться к FSM, так как в кэше у нас уже есть номер подходящей страницы. 

Теперь строки заняли все вакантные места на странице, и при вставке записи придется создавать новую страницу.

INSERT INTO test VALUES (1);

Бэкенд берет номер кэшированной страницы и уже в цикле обнаруживает, что на ней нет необходимого свободного пространства. Следовательно, необходимо записать в FSM обновленную информацию о таргетированной странице и получить номер страницы с необходимым свободным пространством, но, так как в отношении не осталось свободных страниц, нужно выйти из цикла и создать новую.

Таким образом, благодаря кэшированию номеров страниц, в постгресе минимизируется количество обращений к FSM. В ситуациях, когда в FSM не осталось информации о свободном пространстве, бэкенд может последовательно записывать версии строк, обращаясь к FSM только при заполнении страницы основного слоя под завязку, чтобы обновить информацию о ней в FSM.

Выводы

Мы познакомились с внутренним устройством карты свободного пространства, рассмотрев функционал и примеры работы данного слоя, сильно не углубляясь в детали, насколько это было возможно. Также мы убедились, насколько быстро с помощью FSM можно найти нужную страницу, затрачивая по минимуму ресурсов на поддержание нормального состояния древовидной структуры FSM.