Возможно, эта тема не станет открытием для опытных статистиков. Однако я уверен, что менее опытные статистики и R-программисты смогут открыть для себя новые аспекты логистической регрессии, поскольку найти подробности о причинах несовпадения результатов между статистическими пакетами мне удалось только в документации SAS.
Уже больше четырёх лет я занимаюсь биостатистикой, и всё это время я использую в своей работе язык R. RStudio делает его невероятно простым, удобным и в то же время мощным инструментом анализа. Вместе с тем, в течение уже почти года я работаю в контрактно-исследовательской организации (CRO). Бизнес диктует свои стандарты работы, и расчёты для подавляющего большинства серьёзных клинических исследований выполняются на платформе SAS.
SAS как язык неплох и даже в чём-то хорош, хоть и построен на основе ряда странных концепций из далёкого 1976 года, описание которых могло бы стать поводом для отдельной большой статьи. Наличие этих концепций в SAS сегодня вполне объяснимо: ведя свою историю с работы на основе перфокарт, в настоящее время компания вынуждена поддерживать обратную совместимость с предыдущими версиями своих продуктов, поскольку в клинических исследованиях огромное значение имеет концепция воспроизводимости результатов (reproducible research). Это делает невозможным внесение радикальных изменений в синтаксис языка, как это произошло между версиями Python 2.7.x и 3.x. Что действительно грустно — это текущее состояние IDE для SAS, ни одна из которых (в комплекте поставки их три) даже вполовину не так хороша, как RStudio.
Бытует мнение, что переход из SAS в R значительно проще, но моя история сложилась наоборот. Мой способ познавать особенности SAS заключается в сопоставлении полученных в нём результатов с R. Особенно актуальной такая практика стала после случая, когда в ходе двойного программирования оба SAS-программиста неправильно поняли мануал на SAS Help и допустили одну и ту же ошибку в реализации метода. Кроме того, поскольку даже в FDA используют R, очень важно, чтобы потенциальный валидатор смог получить идентичные нашим результаты расчётов.
В одном из исследований нам понадобилось выполнить построение моделей на основе логистической регрессии, чтобы проанализировать возможную взаимосвязь между рядом исходных характеристик пациентов с гепатитом C и успешностью лечения.
Задача довольно тривиальная (но если Вам она не знакома, предлагаю примеры для SAS и для R с хорошим описанием интерпретации). Вопросы возникли, когда результаты обычной univariate logistic regression в нескольких случаях не совпали между двумя пакетами. Чаще всего, конечно, результаты совпадают. Иногда дело лишь в округлении (например, 0.1737 и 0.1738 для p-value). Но в отдельных случаях разница в значениях ?-коэффициентов и вероятностей (p-value) налицо.
Рассмотрим пример с категориальным предиктором «Способ заражения», в котором базовым уровнем фактора выбрано значение «Переливание крови».
Как видно из примера, несмотря на то, что оценки отношений шансов совпадают, значения ?-коэффициентов в моделях различны. При этом значения exp(b) в SAS не совпадают с оценками odds ratio (OR). Что наиболее критично именно для нас — соответствующие ?-коэффициентам значения вероятностей (p-value) совершенно не совпадают с результатами R.
В поисках причины и способа решения возникшего вопроса я неожиданно для себя обнаружил, что сообщества пользователей R и SAS пересекаются очень слабо, и в итоге помочь мне смог только всемогущий Google. Большое спасибо Анне-Марии де Марс, которая при аналогичном сопоставлении результатов SAS с SPSS связалась с представителем SAS и изложила решение в своём блоге, что позволило мне раскрутить цепочку.
Причина различий заключается в способе кодирования уровней фактора, которые используются статистическими пакетами по умолчанию. R и SPSS при построении модели используют подход с кодированием базового уровня (reference cell parameterization, также можно встретить варианты reference coding или dummy coding) и проводят расчёт OR на основе экспоненцирования значений ?-коэффициентов, в то время как SAS применяет другой подход — кодирование эффекта (effect parameterization или effect coding), при котором используется более сложный алгоритм. Подробные примеры построения моделей для этих схем кодирования представлены здесь.
Теперь оценки OR в SAS полностью совпали с экспонентами соответствующих ?-коэффициентов, а значения p-value полностью идентичны результатам R.
Судя по этому материалу, SAS предлагает весьма широкий набор возможных вариантов кодирования уровней фактора при построении моделей. Найти что-то подобное в документации к R мне, к сожалению, не удалось. Буду признателен, если хабражители смогут подсказать такие материалы в комментариях.
Введение
Уже больше четырёх лет я занимаюсь биостатистикой, и всё это время я использую в своей работе язык R. RStudio делает его невероятно простым, удобным и в то же время мощным инструментом анализа. Вместе с тем, в течение уже почти года я работаю в контрактно-исследовательской организации (CRO). Бизнес диктует свои стандарты работы, и расчёты для подавляющего большинства серьёзных клинических исследований выполняются на платформе SAS.
SAS как язык неплох и даже в чём-то хорош, хоть и построен на основе ряда странных концепций из далёкого 1976 года, описание которых могло бы стать поводом для отдельной большой статьи. Наличие этих концепций в SAS сегодня вполне объяснимо: ведя свою историю с работы на основе перфокарт, в настоящее время компания вынуждена поддерживать обратную совместимость с предыдущими версиями своих продуктов, поскольку в клинических исследованиях огромное значение имеет концепция воспроизводимости результатов (reproducible research). Это делает невозможным внесение радикальных изменений в синтаксис языка, как это произошло между версиями Python 2.7.x и 3.x. Что действительно грустно — это текущее состояние IDE для SAS, ни одна из которых (в комплекте поставки их три) даже вполовину не так хороша, как RStudio.
Бытует мнение, что переход из SAS в R значительно проще, но моя история сложилась наоборот. Мой способ познавать особенности SAS заключается в сопоставлении полученных в нём результатов с R. Особенно актуальной такая практика стала после случая, когда в ходе двойного программирования оба SAS-программиста неправильно поняли мануал на SAS Help и допустили одну и ту же ошибку в реализации метода. Кроме того, поскольку даже в FDA используют R, очень важно, чтобы потенциальный валидатор смог получить идентичные нашим результаты расчётов.
Суть вопроса
В одном из исследований нам понадобилось выполнить построение моделей на основе логистической регрессии, чтобы проанализировать возможную взаимосвязь между рядом исходных характеристик пациентов с гепатитом C и успешностью лечения.
Задача довольно тривиальная (но если Вам она не знакома, предлагаю примеры для SAS и для R с хорошим описанием интерпретации). Вопросы возникли, когда результаты обычной univariate logistic regression в нескольких случаях не совпали между двумя пакетами. Чаще всего, конечно, результаты совпадают. Иногда дело лишь в округлении (например, 0.1737 и 0.1738 для p-value). Но в отдельных случаях разница в значениях ?-коэффициентов и вероятностей (p-value) налицо.
Рассмотрим пример с категориальным предиктором «Способ заражения», в котором базовым уровнем фактора выбрано значение «Переливание крови».
Код и результаты R (отклик представлен значениями 0 и 1):

library(haven)
library(car)
setwd("C:/test")
adis <- read_sas("adis.sas7bdat")
adis <- recode(adis, "''= NA")
adis$MODEHCV = factor(adis$MODEHCV,
levels = c("Blood transfusions",
"Dental procedures", "Other"),
ordered = FALSE)
mylogit <- glm(SVR12FL ~ MODEHCV,
data = adis,
family = binomial(link = 'logit'))

Код и результаты SAS (отклик представлен значениями N и Y):
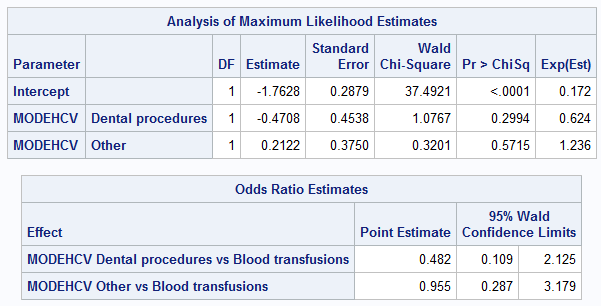
%let dir=C:\test;
LIBNAME source "&dir\DataIN" access=readonly;
DATA adis;
set source.adis;
RUN;
PROC LOGISTIC data = adis;
class MODEHCV (reference = 'Blood transfusions');
model SVR12FL (event = 'Y') = MODEHCV / expb;
RUN;

Как видно из примера, несмотря на то, что оценки отношений шансов совпадают, значения ?-коэффициентов в моделях различны. При этом значения exp(b) в SAS не совпадают с оценками odds ratio (OR). Что наиболее критично именно для нас — соответствующие ?-коэффициентам значения вероятностей (p-value) совершенно не совпадают с результатами R.
Решение
В поисках причины и способа решения возникшего вопроса я неожиданно для себя обнаружил, что сообщества пользователей R и SAS пересекаются очень слабо, и в итоге помочь мне смог только всемогущий Google. Большое спасибо Анне-Марии де Марс, которая при аналогичном сопоставлении результатов SAS с SPSS связалась с представителем SAS и изложила решение в своём блоге, что позволило мне раскрутить цепочку.
Причина различий заключается в способе кодирования уровней фактора, которые используются статистическими пакетами по умолчанию. R и SPSS при построении модели используют подход с кодированием базового уровня (reference cell parameterization, также можно встретить варианты reference coding или dummy coding) и проводят расчёт OR на основе экспоненцирования значений ?-коэффициентов, в то время как SAS применяет другой подход — кодирование эффекта (effect parameterization или effect coding), при котором используется более сложный алгоритм. Подробные примеры построения моделей для этих схем кодирования представлены здесь.
Изменим в SAS схему по умолчанию на reference parameterization
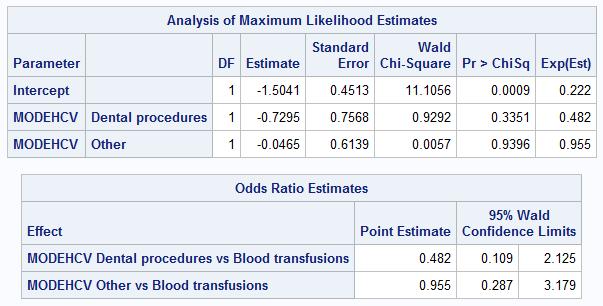
PROC LOGISTIC data = adis;
class MODEHCV (reference = 'Blood transfusions') / param = ref;
model SVR12FL (event = 'Y') = MODEHCV / expb;
RUN;

Теперь оценки OR в SAS полностью совпали с экспонентами соответствующих ?-коэффициентов, а значения p-value полностью идентичны результатам R.
P. S.
Судя по этому материалу, SAS предлагает весьма широкий набор возможных вариантов кодирования уровней фактора при построении моделей. Найти что-то подобное в документации к R мне, к сожалению, не удалось. Буду признателен, если хабражители смогут подсказать такие материалы в комментариях.


Cekory
Может быть, Вам поможет
?contr.SASиoptions(contrasts = c("contr.SAS", "contr.poly"))?