Недавно завершился курс Scalable Machine Learning по Apache Spark, рассказывающий о применении библиотеки MLlib для машинного обучения. Курс состоял из видеолекций и практических заданий. Лабораторные работы необходимо было выполнять на PySpark, а поскольку по работе мне чаще приходится сталкиваться со scala, я решил перерешать основные лабы на этом языке, а заодно и лучше усвоить материал. Больших отличий конечно же нет, в основном, это то, что PySpark активно использует NumPy, а в версии со scala используется Breeze.
Первые два практических занятия охватывали изучение основных операций линейной алгебры в NumPy и знакомство с apache spark соответственно. Собственно машинное обучение началось с третьей лабораторной работы, она и разобрана ниже.
Данная лабораторная работа нацелена на изучение метода линейной регрессии (одного из методов обучения с учителем). Мы будем использовать часть данные от Million Song Dataset. Наша цель заключается в нахождении лучшей модели, предсказывающей год песни по набору аудио характеристик при помощи метода линейной регрессии.
Данная лабораторная работа включает следующие этапы:
1. Чтение, парсинг и обработка данных
2. Создание и оценка базовой модели
3. Реализация базового алгоритма линейной регрессии, обучение и оценка модели
4. Нахождение модели с помощью MLlib, настройка гиперпараметров
5. Добавление зависимостей между характеристиками
Сырые данные в настоящее время хранятся в текстовом файле и представляют собой строки такого вида:
Каждая строка начинается с метки (год выпуска песни), а затем следуют аудио-характеристики записи, разделённые запятой.
Первое, с чего мы начнём: представим данные в виде RDD:
Посмотрим, сколько записей у нас есть:
Что бы лучше понять предоставленные нам данные, давайте визуализируем их, построив тепловую карту хотя бы для части наблюдений. Т.к. характеристики находятся в диапазоне от 0 до 1, то пусть чем ближе значение к единице тем темнее будет оттенок серого, и наоборот.
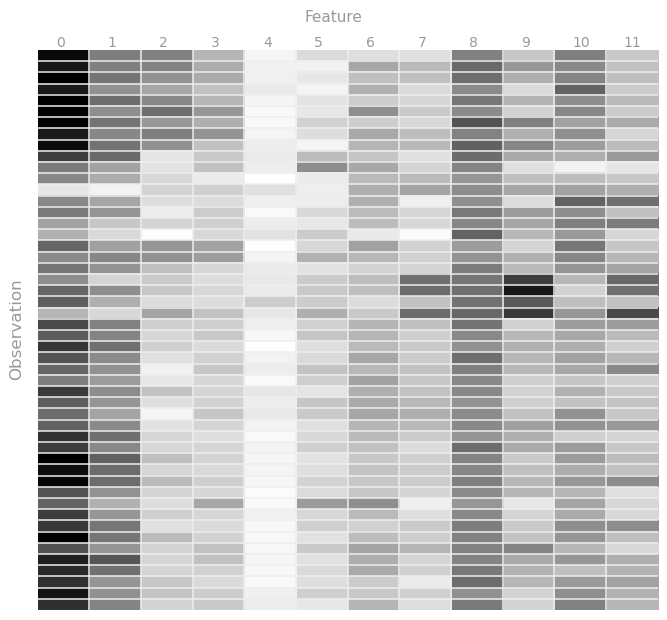
В MLlib обучающая выборка (точнее её элементы) должна храниться в специальном объекте LabeledPoint, который состоит из метки (label) и набора характеристик (features), принадлежащих данной метке. В нашем случае меткой будет год, а характеристиками- аудио- данные записи.
Напишем функцию, которая на вход будет получать одну строку из нашего набора данных и возвращать готовый labeledPoint.
Переведём наши данные в рабочий вариант:
Теперь давайте изучим метки и найдём диапазон годов, в который укладываются наши данные; чтобы это сделать, нужно найти максимальный и минимальный год.
Как мы видим, метки расположены между 1922 и 2011 г.г. В задачах обучения часто является естественным смещение значений так, чтобы они начинались с нуля. Давайте создадим новый RDD, который будет содержать объекты с метками смещёнными на 1922.0.
Мы почти закончили подготовку данных, и всё, что нам осталось- разбить данные на 3 подмножества:
Для этих целей в spark есть метод randomSplit:
Давайте попробуем придумать простую модель, с которой мы могли бы сравнивать точность моделей, полученных в дальнейшем. В самом простом случае модель может выдавать в качестве предсказания среднюю величину года, независимо от входящих данных. Давайте посчитаем эту величину:
Чтобы оценить, насколько хорошо работает наша модель, давайте используем в качестве оценки квадратный корень из среднеквадратической ошибки (RMSE)
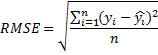 .
.
В нашем случае yi — это метка-год, а yi с крышечкой — это год, предсказанный моделью. Сначала реализуем функцию, вычисляющую квадрат разности label и prediction и функцию, которая будет вычислять RMSE:
Теперь мы можем рассчитать RMSE наших данных на основе предсказаний базовой модели. Для этого подготовим новые RDD содержащие кортежи с наблюдаемыми и прогнозными годами.
Обратите внимание, что каждый полученный RMSE может быть истолкован как средняя ошибка прогнозирования для данного набора (в терминах количества лет)
Теперь, когда у нас есть базовая модель и её оценка, мы можем проверить, сможет ли метод линейной регрессии предложить нам результат лучше предыдущего.
Напомним формулу шага градиентного спуска для линейной регрессии:
wi+1 = wi — ?i * ?(wiT * xj — yj) * xj.
Где i это номер итерации а j идентификатор наблюдения.
Для начала реализуем функцию, которая вычисляет слагаемое для данного обновления (wT * x — y) * x:
Идём дальше: нам необходимо реализовать функцию, которая будет принимать рассчитанные веса модели и наблюдаемые значения, а отдавать — кортеж (наблюдаемое значение, предсказанное значение).
Настало самое время реализовать метод Градиентного спуска:
Ну вот всё готово! Теперь осталось обучить нашу модель линейной регрессии на всей обучающей выборке и оценить её точность на проверочной выборке:
На каждой итерации мы считали RMSE для обучающей выборки и теперь мы можем отследить, как вёл себя алгоритм: для этого построим два графика. Первый- это логарифм ошибки от номера итерации для всех 50 итераций, а второй-собственно значения ошибки для последних 44 итерации.

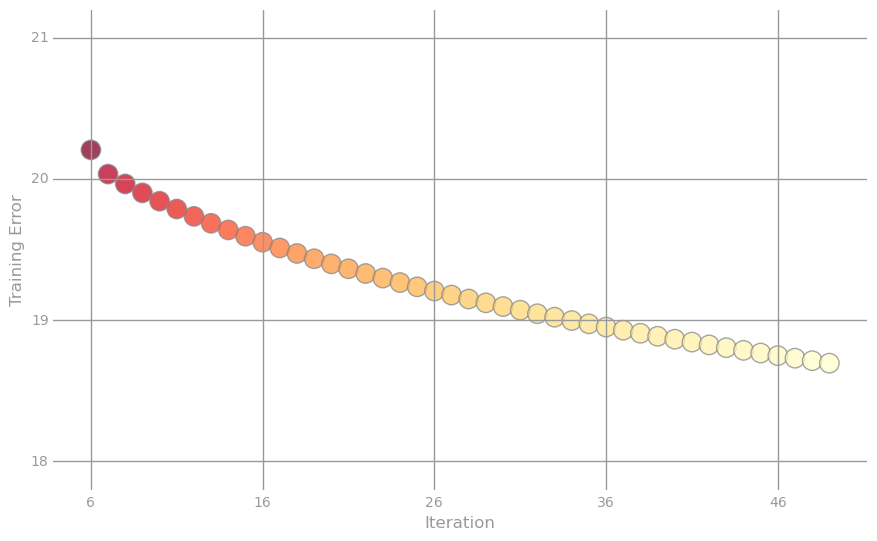
Улучшения мы явно добились: теперь наши предсказания ошибаются в среднем не на 21 год, а всего лишь на 18. Надо отметить, что если количество итераций увеличить до 500, то ошибка будет составлять 16,403.
Ну что же, теперь это выглядит гораздо лучше. Однако давайте посмотрим, можем ли мы улучшить ситуацию, используя свободный член (константа, intercept) и регуляризацию. Для этого мы воспользуемся уже готовым классом LinearRegressionWithSGD, который по существу реализует тот же алгоритм, что и реализовали мы, но более эффективно, с различным дополнительным функционалом, таким, к примеру, как стохастический градиентный спуск, возможность добавление свободного члена, а также L1 и L2 регуляризация.
Для начала, реализуем функцию, которая поможет настроить модель:
Мы использовали RidgeRegressionWithSGD, потому что это обёртка с уже заданным типом регуляризации L2, точно также мы могли бы использовать и LinearRegressionWithSGD, но тогда пришлось бы дописать ещё одну строчку
Запускаем алгоритм:
Результат сравним с нашей реализацией (а если вспомнить, что при равном числе итераций мы получили 16.4, то результат не ахти какой), но, вероятно, мы сможем улучшить результат, пробуя разные значения регуляризации. Давайте посмотрим, что получится, если параметр регуляризации взять 1e-10, 1e-5 и 1.
Осталось проверить, как ведёт себя модель, если изменить значение шага (alpha) и количества итераций. Параметр регуляризации возьмём тот, который дал наилучшее значение, шаг пусть будет 1e-5, 10, а количество итераций 500 и 5.
Итак, мы можем сделать вывод, что при маленьком шаге алгоритм очень медленно приближается к минимуму, а при большом вообще расходится, притом очень быстро.
До сих пор мы использовали только те характеристики, которые нам были предоставлены. Например, если бы у нас было только 2 характеристики x1 и x2, то модель представляла бы собой:
w0 + w1x1 + w2x2.
Однако ничто не мешает нам создать дополнительные характеристики: возвращаясь к нашему примеру, мы могли бы придумать модель и посложнее:
w0 + w1x1 + w2x2 + w3x1x2 + w4x2x1 + w5x12 + w6x22
Давайте так и поступим; для этого нам необходимо реализовать функцию, которая бы попарно перемножала значения характеристик и возвращала бы новый набор, объединённый с исходным.
Теперь давайте создадим новую модель, для этого нам нужно применить функцию описанную выше к нашим наборам данных:
Ну а далее мы должны повторить поиск гиперпараметров для новой модели, т. к. найденные ранее настройки могут не дать наилучший результат. Но мы повторять здесь этого не будем а сразу подставим оптимальные.
Ну и напоследок оценим нашу новую модель на тестовых данных. Обратите внимание что мы не использовали тестовые данные для выбора лучшей модели. Поэтому наша оценка даёт несмещённую оценку того как полученная модель будет работать на новых данных. Теперь мы можем увидеть насколько новая модель лучше базовой.
Ну вот собственно и всё, финальная оценка конечно не выглядит особенно хорошо, но определённо лучше чем та с которой мы стартовали.
Первые два практических занятия охватывали изучение основных операций линейной алгебры в NumPy и знакомство с apache spark соответственно. Собственно машинное обучение началось с третьей лабораторной работы, она и разобрана ниже.
Данная лабораторная работа нацелена на изучение метода линейной регрессии (одного из методов обучения с учителем). Мы будем использовать часть данные от Million Song Dataset. Наша цель заключается в нахождении лучшей модели, предсказывающей год песни по набору аудио характеристик при помощи метода линейной регрессии.
Данная лабораторная работа включает следующие этапы:
1. Чтение, парсинг и обработка данных
2. Создание и оценка базовой модели
3. Реализация базового алгоритма линейной регрессии, обучение и оценка модели
4. Нахождение модели с помощью MLlib, настройка гиперпараметров
5. Добавление зависимостей между характеристиками
1. Чтение, парсинг и обработка данных
Сырые данные в настоящее время хранятся в текстовом файле и представляют собой строки такого вида:
2001.0,0.884123733793,0.610454259079,0.600498416968,0.474669212493,0.247232680947,0.357306088914,0.344136412234,0.339641227335,0.600858840135,0.425704689024,0.60491501652,0.419193351817
Каждая строка начинается с метки (год выпуска песни), а затем следуют аудио-характеристики записи, разделённые запятой.
Первое, с чего мы начнём: представим данные в виде RDD:
val sc = new SparkContext("local[*]", "week3")
val rawData: RDD[String] = sc.textFile("millionsong.txt")
Посмотрим, сколько записей у нас есть:
val numPoints = rawData.count()
println(numPoints)
> 6724
Что бы лучше понять предоставленные нам данные, давайте визуализируем их, построив тепловую карту хотя бы для части наблюдений. Т.к. характеристики находятся в диапазоне от 0 до 1, то пусть чем ближе значение к единице тем темнее будет оттенок серого, и наоборот.

В MLlib обучающая выборка (точнее её элементы) должна храниться в специальном объекте LabeledPoint, который состоит из метки (label) и набора характеристик (features), принадлежащих данной метке. В нашем случае меткой будет год, а характеристиками- аудио- данные записи.
Напишем функцию, которая на вход будет получать одну строку из нашего набора данных и возвращать готовый labeledPoint.
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.mllib.linalg.Vectors
def parsePoint(line: String) = {
val sp = line.split(',')
LabeledPoint(sp.head.toDouble, Vectors.dense(sp.tail.map(_.toDouble)))
}
Переведём наши данные в рабочий вариант:
val parsedDataInit: RDD[LabeledPoint] = rawData.map(parsePoint)
Теперь давайте изучим метки и найдём диапазон годов, в который укладываются наши данные; чтобы это сделать, нужно найти максимальный и минимальный год.
val onlyLabels = parsedDataInit.map(_.label)
val minYear = onlyLabels.min()
val maxYear = onlyLabels.max()
println(s"max: $maxYear, min: $minYear")
> max: 2011.0, min: 1922.0
Как мы видим, метки расположены между 1922 и 2011 г.г. В задачах обучения часто является естественным смещение значений так, чтобы они начинались с нуля. Давайте создадим новый RDD, который будет содержать объекты с метками смещёнными на 1922.0.
val parsedData = parsedDataInit.map(x => LabeledPoint(x.label - minYear, x.features))
Мы почти закончили подготовку данных, и всё, что нам осталось- разбить данные на 3 подмножества:
- обучающая выборка — именно на ней мы и будем обучать нашу модель
- проверочная выборка — на этих данных мы будем проверять насколько успешно обученная модель предсказывает результат
- тестовая выборка — этот набор будет имитировать новые данные и поможет нам правдиво оценить лучшую модель
Для этих целей в spark есть метод randomSplit:
val weights = Array(0.8, 0.1, 0.1)
val seed = 42
val splitData: Array[RDD[LabeledPoint]] = parsedData.randomSplit(weights, seed).map(_.cache())
val parsedTrainData = splitData(0)
val parsedValData = splitData(1)
val parsedTestData = splitData(2)
val nTrain = parsedTrainData.count()
val nVal = parsedValData.count()
val nTest = parsedTestData.count()
println(nTrain, nVal, nTest, nTrain + nVal + nTest)
println(parsedData.count())
>(5402,622,700,6724)
> 6724
2. Создание и оценка базовой модели
Давайте попробуем придумать простую модель, с которой мы могли бы сравнивать точность моделей, полученных в дальнейшем. В самом простом случае модель может выдавать в качестве предсказания среднюю величину года, независимо от входящих данных. Давайте посчитаем эту величину:
val averageTrainYear = parsedTrainData.map(_.label).mean()
println(averageTrainYear)
> 53.68659755646054
Чтобы оценить, насколько хорошо работает наша модель, давайте используем в качестве оценки квадратный корень из среднеквадратической ошибки (RMSE)
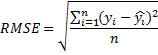 .
.В нашем случае yi — это метка-год, а yi с крышечкой — это год, предсказанный моделью. Сначала реализуем функцию, вычисляющую квадрат разности label и prediction и функцию, которая будет вычислять RMSE:
def squaredError(label: Double, prediction: Double) = math.pow(label - prediction, 2)
def calcRMSE(labelsAndPreds: RDD[(Double, Double)]) =
math.sqrt(labelsAndPreds.map(x => squaredError(x._1, x._2)).sum() / labelsAndPreds.count())
Теперь мы можем рассчитать RMSE наших данных на основе предсказаний базовой модели. Для этого подготовим новые RDD содержащие кортежи с наблюдаемыми и прогнозными годами.
val labelsAndPredsTrain = parsedTrainData.map(x => x.label -> averageTrainYear)
val rmseTrainBase = calcRMSE(labelsAndPredsTrain)
val labelsAndPredsVal = parsedValData.map(x => x.label -> averageTrainYear)
val rmseValBase = calcRMSE(labelsAndPredsVal)
val labelsAndPredsTest = parsedTestData.map(x => x.label -> averageTrainYear)
val rmseTestBase = calcRMSE(labelsAndPredsTest)
> Base model:
Baseline Train RMSE = 21,496
Baseline Validation RMSE = 21,100
Baseline Test RMSE = 21,100
Обратите внимание, что каждый полученный RMSE может быть истолкован как средняя ошибка прогнозирования для данного набора (в терминах количества лет)
3. Реализация базового алгоритма линейной регрессии, обучение и оценка модели
Теперь, когда у нас есть базовая модель и её оценка, мы можем проверить, сможет ли метод линейной регрессии предложить нам результат лучше предыдущего.
Напомним формулу шага градиентного спуска для линейной регрессии:
wi+1 = wi — ?i * ?(wiT * xj — yj) * xj.
Где i это номер итерации а j идентификатор наблюдения.
Для начала реализуем функцию, которая вычисляет слагаемое для данного обновления (wT * x — y) * x:
import breeze.linalg.{ DenseVector => BreezeDenseVector }
def gradientSummand(weights: BreezeDenseVector[Double], lp: LabeledPoint): BreezeDenseVector[Double] = {
val x = BreezeDenseVector(lp.features.toArray)
val y = lp.label
val wx: Double = weights.t * x
(wx - y) * x
}
Идём дальше: нам необходимо реализовать функцию, которая будет принимать рассчитанные веса модели и наблюдаемые значения, а отдавать — кортеж (наблюдаемое значение, предсказанное значение).
def getLabeledPrediction(weights: BreezeDenseVector[Double], observation: LabeledPoint): (Double, Double) = {
val x = BreezeDenseVector(observation.features.toArray)
val y = observation.label
val prediction: Double = weights.t * x
(y, prediction)
}
Настало самое время реализовать метод Градиентного спуска:
def linregGradientDescent(trainData: RDD[LabeledPoint], numIters: Int) = {
// Размер обучающей выборки
val n = trainData.count()
// Кол-во характеристик
val d = trainData.first().features.size
// Создаём начальный вектор весов (состоит из d нулей)
val w = BreezeDenseVector.zeros[Double](d)
val alpha = 1.0
val errorTrain = BreezeDenseVector.zeros[Double](numIters)
for (i <- 0 until numIters) {
val labelsAndPredsTrain = trainData.map(x => getLabeledPrediction(w, x))
errorTrain(i) = calcRMSE(labelsAndPredsTrain)
val gradient: BreezeDenseVector[Double] = trainData.map(x => gradientSummand(w, x)).reduce((dv1, dv2) => dv1 + dv2)
val alpha_i = alpha / ( n * math.sqrt(i+1) )
w -= alpha_i * gradient
}
(w, errorTrain)
}
Ну вот всё готово! Теперь осталось обучить нашу модель линейной регрессии на всей обучающей выборке и оценить её точность на проверочной выборке:
val numIters = 50
val (weightsCustom, errorTrainCustom) = linregGradientDescent(parsedTrainData, numIters = numIters)
val labelsAndPreds = parsedValData.map(lp => getLabeledPrediction(weightsCustom, lp))
val rmseValLRCustom = calcRMSE(labelsAndPreds)
> Custom Linear regression algorithm
Weights = DenseVector(22.429559050840954, 20.57848949803509, -0.38069311013701224, 8.286892767462648, 5.725188813272974, -4.547779089973534, 15.494323154076804, 3.7888305696294986, 10.205862111138764, 5.877745123091225, 11.13061973187094, 3.6849419014146703)
Baseline = 21,100
CustomLR = 18,341
На каждой итерации мы считали RMSE для обучающей выборки и теперь мы можем отследить, как вёл себя алгоритм: для этого построим два графика. Первый- это логарифм ошибки от номера итерации для всех 50 итераций, а второй-собственно значения ошибки для последних 44 итерации.


Улучшения мы явно добились: теперь наши предсказания ошибаются в среднем не на 21 год, а всего лишь на 18. Надо отметить, что если количество итераций увеличить до 500, то ошибка будет составлять 16,403.
4. Нахождение модели с помощью MLlib, настройка гиперпараметров
Ну что же, теперь это выглядит гораздо лучше. Однако давайте посмотрим, можем ли мы улучшить ситуацию, используя свободный член (константа, intercept) и регуляризацию. Для этого мы воспользуемся уже готовым классом LinearRegressionWithSGD, который по существу реализует тот же алгоритм, что и реализовали мы, но более эффективно, с различным дополнительным функционалом, таким, к примеру, как стохастический градиентный спуск, возможность добавление свободного члена, а также L1 и L2 регуляризация.
Для начала, реализуем функцию, которая поможет настроить модель:
import org.apache.spark.mllib.regression.RidgeRegressionWithSGD
def tuneModel(numIterations: Int = 500, stepSize: Double = 1.0, regParam: Double = 1e-1) = {
val model = new RidgeRegressionWithSGD()
model.optimizer
.setStepSize(stepSize)
.setNumIterations(numIterations)
.setRegParam(regParam)
model.setIntercept(true)
}
Мы использовали RidgeRegressionWithSGD, потому что это обёртка с уже заданным типом регуляризации L2, точно также мы могли бы использовать и LinearRegressionWithSGD, но тогда пришлось бы дописать ещё одну строчку
model.optimizer.setUpdater(new SquaredL2Updater)Запускаем алгоритм:
val ridgeModel = tuneModel(numIterations = 500, stepSize = 1.0, regParam = 1e-1).run(parsedTrainData)
val weightsRidge = ridgeModel.weights
val interceptRidge = ridgeModel.intercept
val rmseValRidge = calcError(ridgeModel, parsedValData)
> RidgeRegressionWithSGD
weights = [16.49707401343799,15.090143596016913,-0.33882414671890876,6.21399054657087,3.9399959912276765,-3.326873353072514,11.219894673155363,2.605614334247694,7.368594539065305,4.352602095699236,7.936294197372791,2.597979499976716]
intercept = 13.40151357030002
> RidgeRegressionWithSGD validation RMSE
Baseline = 21,100
CustomLR = 18,341
RidgeLR = 18,924
Результат сравним с нашей реализацией (а если вспомнить, что при равном числе итераций мы получили 16.4, то результат не ахти какой), но, вероятно, мы сможем улучшить результат, пробуя разные значения регуляризации. Давайте посмотрим, что получится, если параметр регуляризации взять 1e-10, 1e-5 и 1.
var bestRMSE = rmseValRidge
var bestRegParam = 1.0
var bestModel = ridgeModel
for (regParam <- Array(1e-10, 1e-5, 1)) {
val model = tuneModel(regParam = regParam).run(parsedTrainData)
val rmseVal = calcError(model, parsedValData)
println(f"regParam = $regParam%.0e, RMSE = $rmseVal%.3f")
if (rmseVal < bestRMSE) {
bestRMSE = rmseVal
bestRegParam = regParam
bestModel = model
}
}
> regParam = 1e-10, RMSE = 16,292
regParam = 1e-05, RMSE = 16,292
regParam = 1e+00, RMSE = 23,179
> Best model
weights = [29.417184432817606,31.186800575308965,-17.37215928935944,8.288971260120093,5.111705048981693,-22.61199371516979,25.231243109503467,-4.989933439427709,6.709806469376133,-0.08589332350175394,9.958713420381914,-6.252319073419468]
intercept = 16.170147238736043
regParam = 1.0E-10
> Grid validation RMSE
Baseline = 21,100
LR0 = 18,341
LR1 = 18,924
LRGrid = 16,292
Осталось проверить, как ведёт себя модель, если изменить значение шага (alpha) и количества итераций. Параметр регуляризации возьмём тот, который дал наилучшее значение, шаг пусть будет 1e-5, 10, а количество итераций 500 и 5.
for (alpha <- Array(1e-5, 10)) {
for (numIter <- Array(5, 500)) {
val model = tuneModel(numIterations = numIter, stepSize = alpha, regParam = bestRegParam).run(parsedTrainData)
val rmseVal = calcError(model, parsedValData)
println(f"alpha = $alpha%.0e, numIters = $numIter, RMSE = $rmseVal%.3f")
}
}
> alpha = 1e-05, numIters = 5, RMSE = 56,912
alpha = 1e-05, numIters = 500, RMSE = 56,835
alpha = 1e+01, numIters = 5, RMSE = 351471078,741
alpha = 1e+01, numIters = 500, RMSE = 3696615731186115000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000,000
Итак, мы можем сделать вывод, что при маленьком шаге алгоритм очень медленно приближается к минимуму, а при большом вообще расходится, притом очень быстро.
5. Добавление зависимостей между характеристиками
До сих пор мы использовали только те характеристики, которые нам были предоставлены. Например, если бы у нас было только 2 характеристики x1 и x2, то модель представляла бы собой:
w0 + w1x1 + w2x2.
Однако ничто не мешает нам создать дополнительные характеристики: возвращаясь к нашему примеру, мы могли бы придумать модель и посложнее:
w0 + w1x1 + w2x2 + w3x1x2 + w4x2x1 + w5x12 + w6x22
Давайте так и поступим; для этого нам необходимо реализовать функцию, которая бы попарно перемножала значения характеристик и возвращала бы новый набор, объединённый с исходным.
def twoWayInteractions(lp: LabeledPoint) = {
val features: List[Double] = lp.features.toArray.toList
val two = (for (x <- features; y <- features) yield (x,y)).map(x => x._1 * x._2)
val inter = two ::: features
LabeledPoint(lp.label, Vectors.dense(inter.toArray))
}
Теперь давайте создадим новую модель, для этого нам нужно применить функцию описанную выше к нашим наборам данных:
val trainDataInteract = parsedTrainData.map(twoWayInteractions)
val valDataInteract = parsedValData.map(twoWayInteractions)
val testDataInteract = parsedTestData.map(twoWayInteractions)
Ну а далее мы должны повторить поиск гиперпараметров для новой модели, т. к. найденные ранее настройки могут не дать наилучший результат. Но мы повторять здесь этого не будем а сразу подставим оптимальные.
val modelInteract = tuneModel(regParam = bestRegParam).run(trainDataInteract)
val rmseValLRInteract = calcError(modelInteract, valDataInteract)
> Interact validation RMSE
Baseline = 21,100
LR0 = 18,341
LR1 = 18,924
LRGrid = 16,292
LRInteract = 15,225
Ну и напоследок оценим нашу новую модель на тестовых данных. Обратите внимание что мы не использовали тестовые данные для выбора лучшей модели. Поэтому наша оценка даёт несмещённую оценку того как полученная модель будет работать на новых данных. Теперь мы можем увидеть насколько новая модель лучше базовой.
> Test validation RMSE
Baseline = 21,100
LRInteract = 15,905
Ну вот собственно и всё, финальная оценка конечно не выглядит особенно хорошо, но определённо лучше чем та с которой мы стартовали.
Комментарии (6)

Tutufa
05.08.2015 13:12+6Вообще говоря там ясно просили решения домашек на гитхаб и в блоги не выкладывать.

alexeygrigorev
05.08.2015 15:07+2В новом Mahout такие вычисления делать намного проще. Вот даже статья есть — про тот же самый набор данных www.itshared.org/2015/04/apache-mahout-samsara-quick-start.html

ajvol
05.08.2015 19:47похоже, этот же подход можно использовать для определения песен, опередивших своё время

Optik
06.08.2015 07:22Лабы в курсе были ванильные, там думать даже не надо было. Заполнить в редких местах пробелы и только. Вы же её тупо перепечатали на другом ЯП (тем более в случае спарка интерфейсы скалы и питона почти полностью совпадают). Судя по листингам, тупо var val проставлено у переменных и местами скобочки.
Кабздец. Уже на второй день изучения скалы никто так не напишет. Переделка питоновского кода.for (alpha <- Array(1e-5, 10)) { for (numIter <- Array(5, 500)) { val model = tuneModel(numIterations = numIter, stepSize = alpha, regParam = bestRegParam).run(parsedTrainData) val rmseVal = calcError(model, parsedValData) println(f"alpha = $alpha%.0e, numIters = $numIter, RMSE = $rmseVal%.3f") } }
С учетом нарушения просьбы не распространять лабы, вы получаетесь бесчестный копипастер.


Dreamastiy
Ждем реализацию на Scala лабы с PCA и визуализацией активности мозга рыбы.
P.S. Honor Code, кстати, статьей не нарушается?
Cthulhu
Нарушается.