27.02.2020 12:16
ilvokhin 10 2800 Источник


Я хочу рассказать о том, что такое граф знаний и об одном из способов его построения из нескольких тематических источников.

Большое количество запросов в поиске содержат единственную сущность — объект, про который спрашивает пользователь. Это могут быть запросы про каких-то людей, фильмы, сериалы, музыкальные или географические объекты. Когда пользователь задает такой запрос, в выдаче ему можно показать дополнительную информационную карточку в надежде, что информация в карточке будет интересна пользователю. Карточки украшают выдачу и повышают ее наглядность. С помощью информационных карточек мы даём человеку понять, что он пользуется интеллектуальным сервисом, потому что поисковая система поняла, что он имел в виду, о каком именно объекте спрашивал. Более того, эту интеллектуальность можно расширить, отвечая на запрос пользователя прямо на странице выдачи. Например, в ответ на «что посмотреть в Праге» мы можем сразу показать достопримечательности этого города.

Бывают случаи, когда пользователь хочет узнать что-то о каком-то объекте, но совершенно ничего о нём не знает, кроме факта его существования. Или пользователь хочет продолжить исследования по какой-то теме. Специально для этого случая в карточке показывается то, чем известен этот объект, а также возможные варианты для продолжения исследования в блоке «cмотрите также».

Граф знаний


В основе всех этих семантических технологий лежит граф знаний — это граф, узлами которого являются объекты реального мира, а переходами — типизированные отношения между объектами (например, отношение для места рождения отличается от отношения даты рождения). Пример маленького графа знаний показан на рис. 1.


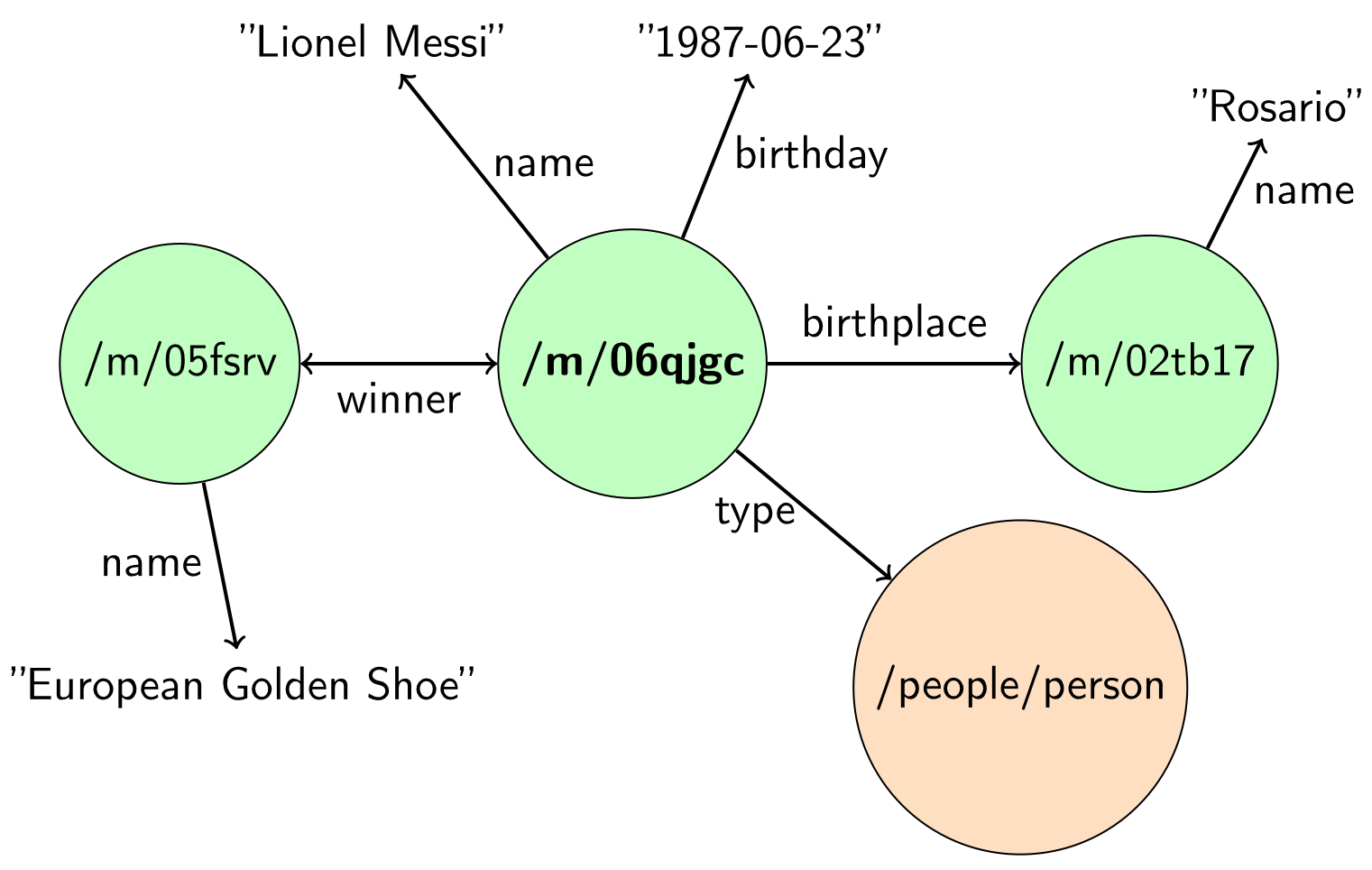
Рис. 1. Пример графа знаний

Существуют открытые графы знаний, которые можно скачать и использовать. Примеры и некоторая статистика по самым известным открытым графам знаний представлена в табл. 1.

Таблица. 1. Статистика по открытым графам знаний

Граф знаний Количество записей Количество объектов Частота обновления
Freebase Более 3 миллиардов 49 миллионов Не обновляется
Викиданные 748 миллионов 18 миллионов Раз в неделю (инкрементально — раз в сутки)
DBpedia 411 миллиона 4 миллиона Последнее обновление в августе 2019

Проблема открытых графов заключается в том, что не все сферы знаний освещены достаточно глубоко. Например, российские сериалы. Они не очень популярны во всем мире, но нам особенно дороги, потому что пользователи спрашивают про них. Это значит, что мы должны найти какую-то информацию об этих сериалах и принести её на SERP (Search Engine Result Page). Вторая проблема — это довольно редкие обновления. А ведь когда случается какое-то событие, мы хотим как можно скорее принести эту информацию и показать её на страницах с результатами поиска.

Существует как минимум три возможных решения этих проблем.

Первое: ничего не делать, смириться, закрыть на это глаза и продолжать жить. Второе: аккуратно вручную добавлять информацию в открытые графы знаний, а потом пользоваться данными оттуда. И третий вариант: автоматически слить с графом знания из какого-то тематического источника. Для тех же фильмов и сериалов таких источников довольно много: КиноПоиск, IMDb, Кино Mail.ru. Причем в графах знаний, как правило, у объектов присутствуют ссылки на популярные тематические ресурсы.

Мы начали реализовывать третий подход. Прежде, чем приступать к решению этой задачи, нужно подготовиться. Дело в том, что данные в источниках представлены в разных форматах. Например, в Викиданных — это JSON, в КиноПоиске — HTML. Их нужно сконвертировать в одинаковый формат. Мы конвертируем в N-Triples, потому что его удобно обрабатывать параллельно, а в данном случае это действительно важно, так как мы работаем с большими данными. Разжатый JSON-дамп Викиданных занимает около 720 Гб, а HTML-страницы КиноПоиска 230 Гб, поэтому почти все задачи решаются на кластере с помощью парадигмы MapReduce.

Склейка дублей


Одной из самых сложных задач при слиянии графов знаний является склейка дублей. Например, у нас есть графы и два каких-то объекта в них, которые являются одним объектом реального мира. Мы хотим в нашем результирующем графе склеить их вместе так, чтобы это был один объект в графе знаний. Решение, которое мы придумали с самого начала, довольно простое. Давайте мы возьмем и склеим все объекты, у которых одинаковые имена. Так мы узнали, что существует, как минимум, два известных человека с именем Брэд Питт, чуть менее сорока фильмов и сериалов под названием «Мост», и примерно столько же Иванов Ивановых про которых есть статья на Википедии.

Очевидно, что такой простой подход не работает, требуется что-то посложнее. И тогда мы придумали решение из трёх частей. Первая часть — это генератор кандидатов для связывания. Вторая — классификатор, который пытается ответить на вопрос, нужно ли склеивать между собой пару объектов. И третья — это дополнительный шаг склейки: мы доклеиваем то, что не получилось по каким-то причинам склеить на предыдущем шаге.

Генератор нужен для того, чтобы сократить количество кандидатов для связывания (пытаться связать каждый объект с каждым слишком дорого). Поэтому мы ограничиваемся лишь небольшим множеством кандидатов и после запускаем классификатор только для этого небольшого множества. Основная идея заключается в том, что имена объектов, которые могут быть связаны, должны каким-то образом быть похожи. Мы решили начать с полного совпадения подстрок, но с возможностью перестановки слов. Это значит, что если у двух объектов порядок слов в имени не совпадает (например, имя и фамилия человека перепутаны местами), они всё равно будут сопоставлены. Мы используем как русские имена, так и оригинальные иностранные. Также мы используем прозвища, псевдонимы и синонимы объектов, которые мы собрали из перенаправлений Википедии.

Прежде чем обучать модель, неплохо бы откуда-то получить данные. Нам повезло, всё необходимое уже было в открытых графах знаний. Например, в Викиданных чуть менее 200 тыс. объектов, ссылок на фильмы и сериалы КиноПоиска, и чуть менее 100 тыс. ссылок на персон КиноПоиска. На этих данных мы и будем обучаться.

В основе всех признаков лежит идея, что один и тот же объект в двух графах должен иметь схожий контекст. Похожая идея используются при решении задачи Entity Linking. Причем под контекстом в графе подразумеваются не соседние объекты к данному объекту, а их строковые описания. Более формально контекстом объекта в графе будут считаться все смежные ему строки, а также имена инцидентных ему объектов и типы. На рис. 2 строки, которые принадлежат контексту этого объекта, выделены жирным.


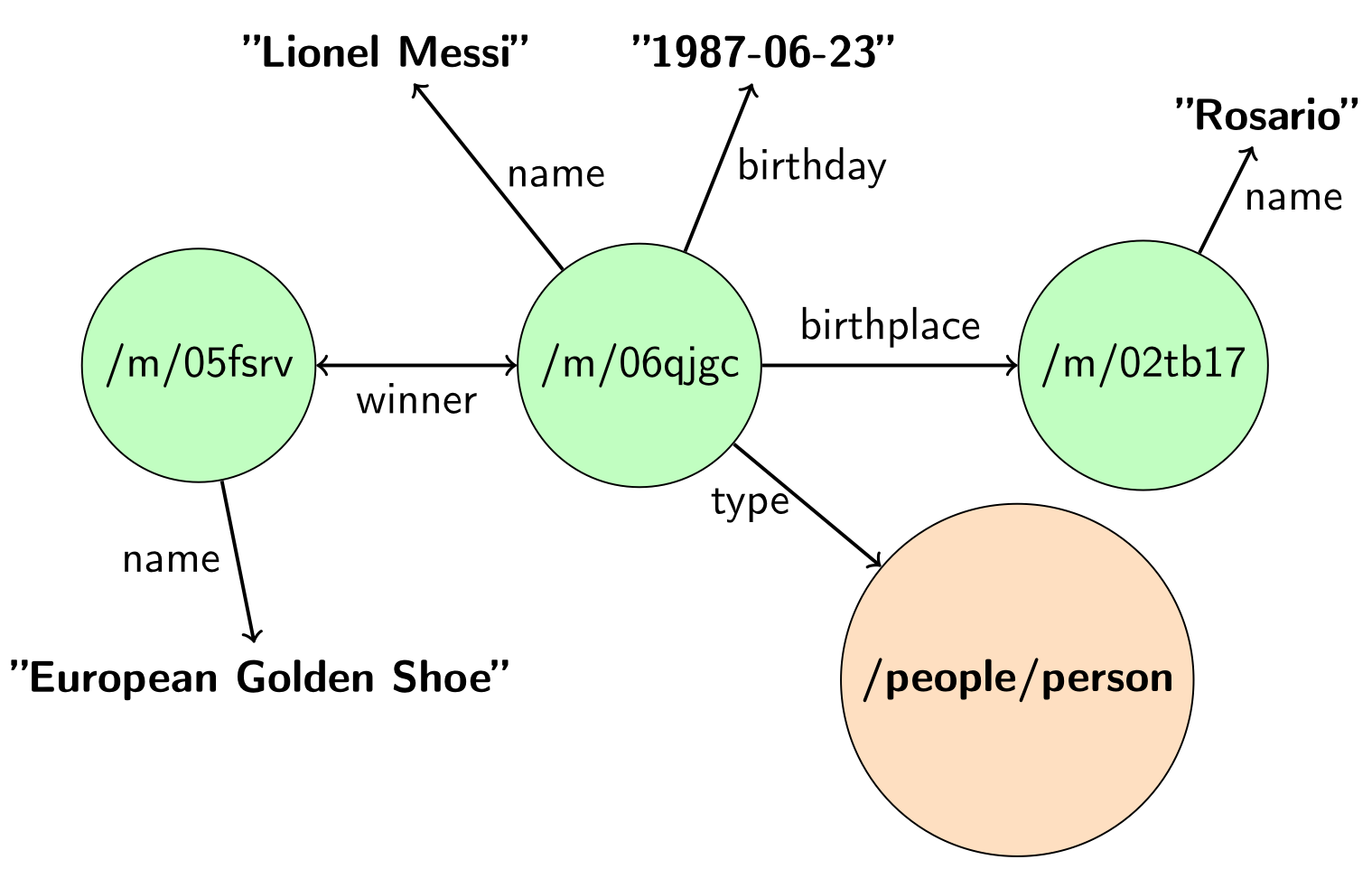
Рис. 2. Контекст объекта

Работать со строками можно несколькими способами. Во-первых, считать совпадение строк, сопоставляя их целиком, то есть учитывая только полное совпадение. Во-вторых, можем пользоваться строкой как мешком слов, разбить строку на слова и пожертвовать порядком. Мы используем оба подхода.

Строки можно либо использовать сразу все вместе, либо группировать по видам отношений, которыми они связаны с объектом. Считаются также абсолютные и относительные совпадения по группам.

Возьмём два объекта: Лионель Месси (Lionel Messi) и Лайонел Ричи (Lionel Richie), табл. 2.

Таблица. 2. Некоторые отношения для объектов «Лионель Месси» и «Лайонел Ричи».

Имя отношения Лионель Месси Лайонел Ричи
name «Lionel Messi» «Lionel Richie»
birthday «June 24, 1987» «June 20, 1949»
football_club «FC Barcelona» —

Имена не совпадают целиком, поэтому полное совпадение в имени будет равно нулю. Но количество совпадений слов в имени равно 1, потому что оригинальное имя «Lionel» совпадает у обоих объектов. Коэффициент Жаккара (отношение размера пересечения к размеру объединения) для имени будет равен 0.2:

$J(Messi, Richie) = \frac{\left |«Lionel» \right |}{\left |«Лионель», «Месси», «Lionel», «Messi», «Richie» \right |}$


Мы не сразу поняли, что если у какого-то объекта не хватает нужного отношения, то не имеет смысла торопиться и записывать в этот признак нуль, лучше записать Missing value. Ведь когда мы добавляем к большому графу какой-то тематический граф, в нём часто отсутствуют какие-то отношения, и нужно иметь возможность различать случаи, когда в двух отношениях ничего не совпало, и когда у какого-то из объектов просто не хватает нужного отношения. Следуя этой логике количество совпавших слов для отношения «football_club» будет равно Missing value. Количество полных совпадений строк по всем отношениям равно нулю, а количество совпавших слов — два («Lionel» и «June»).

Рейтинг лучших признаков, используемых моделью показан на рис. 3.


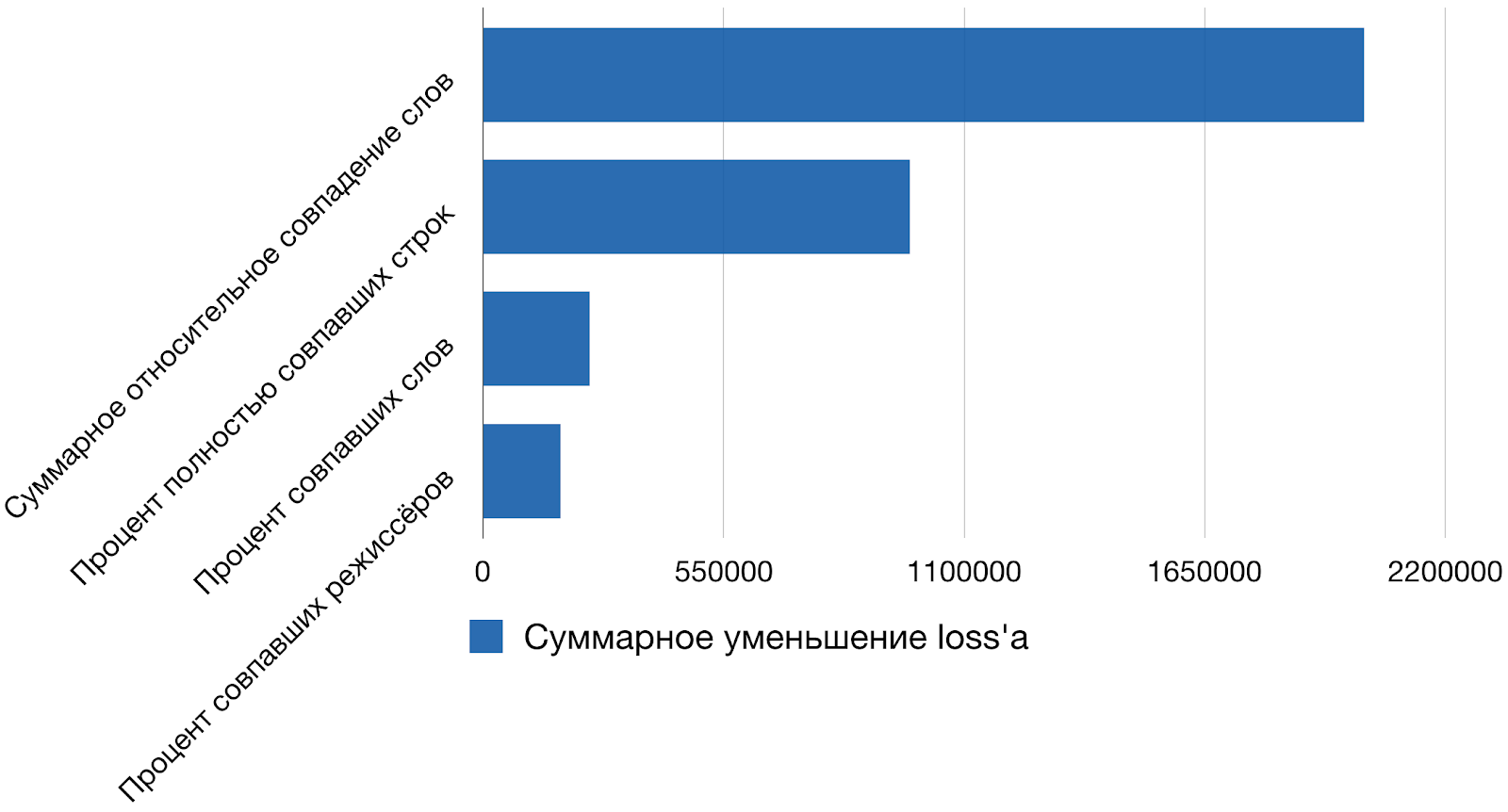
Рис. 3. Самые важные из используемых признаков

Лучшим признаком у нашей модели считается суммарное относительное совпадение слов. За этим сложным названием скрывается сумма коэффициентов Жаккара по всем отношениям. Интересно, что если вообще выбросить всё машинное обучение из этой задачи и оставить более-менее адекватную отсечку по значению этого признака, то качество модели по $F_{1}$-мере упадет всего на 20 %. Если взять признаки, которые описаны выше, обучить на них XGBoost из коробки, 250 деревьев высотой 4, то мы получим довольно неплохие метрики.

Таблица. 3. Метрики качества модель на тестовых данных.

Имя метрики Значение
Точность (precision) 0.961531
Полнота (recall) 0.963220
$F_{1}$ 0.962375
AUC 0.999589

Но есть проблема: на этих метриках не видно некоторых объектов, которые мы не склеиваем. Это так называемые «большие объекты» у которых много отношений. Города, страны, род занятий — это те объекты, которые связаны с большим количеством других объектов. На рис. 4 показано, как это может выглядеть на SERP. Кажется, что все довольно безобидно:


Рис. 4. Проблема «больших» объектов

У нас в карточке есть дубли. Казалось бы, ничего страшного, но на самом деле проблема намного глубже, страдает согласованность данных. Так происходит потому, что в наших обучающих данных совсем нет подобных объектов. Здесь нужно применить другой подход, использовать большое количество отношений этих объектов себе во благо. На рис. 5 показана схема такого подхода. Пусть есть два объекта X и Y, которые связал классификатор. Эти объекты принадлежат разным графам и каждый объект связан с какими-то другими объектами в своем графе. Объект X связан с объектами A, B, C с помощью отношений $r_{1}$, $r_{2}$, $r_{3}$, а объект Y с объектами D, E и F c помощью отношений $r_{1}$, $r_{2}$ и $r_{4}$. Но теперь нам известно, что объекты X и Y на самом деле являются одним объектом реального мира.


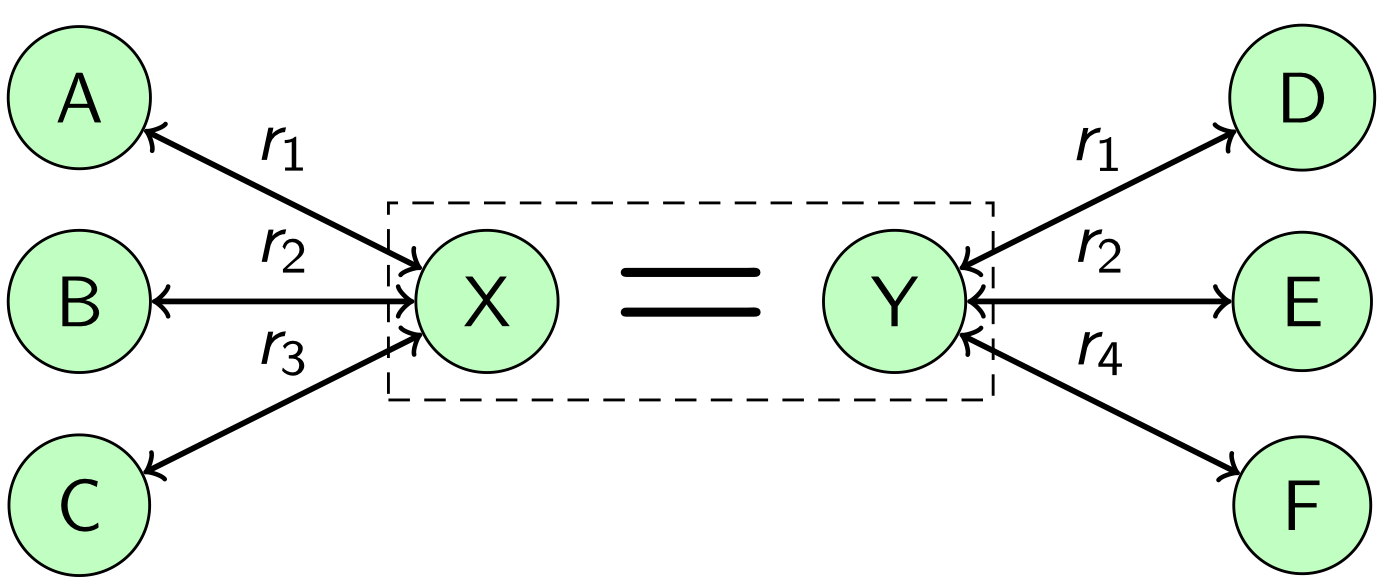
Рис. 5. Дополнительная склейка

Давайте выдвинем две гипотезы:

  • $H_{1}: P(D | A) = p = P(D | ¬A)$ — объект $D$ никак не связан и встречается независимо от объекта $A$.
  • $H_{2}: P(D | A) = p_{1}\neq p_{2} = P(D | ¬A)$ — какая-то зависимость между $D$ и $A$ всё-таки есть.

Тогда мы сможем применить Likelihood-ratio тест и принять одну из двух гипотез. Таким образом у нас получится склеить большие объекты.

Итоговое решение получилось довольно универсальным, поэтому похожим образом можно склеивать дубли и для других тематических источников, постоянно увеличивая охват и глубину тем в графе знаний.

Заключение


В статье рассмотрено одно из возможных решений задачи склейки одинаковых объектов разных графов знаний. Когда граф знаний уже построен, мы можем показать информационные карточки на странице с поисковыми результатами, использовать знания из графа для ответа на вопросы-фактоиды или придумать еще какое-то интересное применение, чтобы порадовать пользователей.

Надеюсь, что было интересно почитать немного о том, как это все работает изнутри. Если остались какие-то непонятные моменты, пожалуйста, задавайте вопросы, попробую на них ответить.