Всем привет.

Есть такая задача – проверить, являются ли два графа изоморфными друг другу. Т.е., говоря по-простому, узнать, являются ли оба эти графа «одним и тем же» графом, но с разной нумерацией вершин и, в случае задания графов графически, с разным их пространственным расположением. Решение этой задачи не является таким уж очевидным, как может кому-то показаться на первый взгляд: даже для небольших графов взгляд на их графическое представление не всегда даст однозначный ответ. См., например, рисунок в той же Вики: ru.wikipedia.org/wiki/Изоморфизм_графов#Пример.

Ну как, очевидно?

А есть и более сложная задача: поиск в некотором «большом» графе всех подграфов, изоморфных некоторому другому графу «поменьше». Это еще более «темный лес». То есть, конечно, не совсем темный, но задача, согласитесь, не самая простая.

Итак, что же мы имеем?

1. Зачем вообще все это надо

И хотя задача про изоморфные (под)графы, как мы уже упомянули, сложная, она довольно нужная и полезная. А зачем? А затем, например, чтобы искать в базе данных химические соединения, подобные некоторой заданной молекуле по ее структурной формуле. Ведь ее можно представить себе в виде графа, не так ли? Этим занимается хемоинформатика – есть такая наука. А ведь есть еще задачи сопоставления с образцом, различные биоинформатические задачи, да много всего интересного.

2. Как решают эту задачу?

Классический подход к решению данной задачи был заложен Дж. Ульманом в 1976 году [3], впоследствии он существенно доработал свой алгоритм [4]. Также данный подход получил дальнейшее развитие в работах многих других авторов, например, Корделлы и соавторов [2] (алгоритм VF2), Бонници и соавторов [1] (алгоритм RI), и др.

Если кратко, то суть этого подхода заключается в «умном переборе» возможных соответствий вершин графа-образца B и графа A, в котором идет его поиск. «Умным» этот перебор делает ввод различных условий и ограничений, которые позволяют как можно раньше отсечь неподходящие варианты. Также для этих целей может проводиться различная предварительная обработка исходных данных.

Не будем здесь заниматься пересказом данных работ, а предложим читателю познакомиться с ними самостоятельно. Однако «показ лучше наказа», и, нужно отметить, что в Сети есть и неплохие графические примеры и объяснения этих алгоритмов. См., например, следующие:
coderoad.ru/17480142/Есть-ли-простой-пример-для-объяснения-алгоритма-Ульмана – очень хорошее и понятное объяснение с примером,
issue.life/questions/8176298 – шаги алгоритма VF2 с примером.

Однако возникает вопрос – возможны ли также еще какие-либо иные пути и подходы для решения этой задачи, пусть и для каких-то частных случаев? И вот с одним из возможных ответов на этот вопрос и хотелось бы Вас познакомить.

2. Изоморфизм графов и NB-пути

Давайте сразу договоримся: под NB-путями (и не из англомании, а просто потому, что так – короче) мы будем называть maximal non-branching paths, т.е. максимально протяженные неразветвляющиеся пути некоторого графа.

Итак, если у нас если два графа изоморфны друг другу, то для любого представления первого графа в виде последовательности максимально протяженных неразветвляющихся путей (т.е. этих наших NB-путей) всегда существует соответствующее ему такое же представление второго графа, и при этом:

• для ориентированных графов соответствующие друг другу пути будут сонаправлены,
• степени соответствующих друг другу вершин для неориентированных графов (а для ориентированных – количества входящих и исходящих ребер соответственно) будут равны,
• при «совмещении» таких представлений в результате мы будем иметь соответствие вершин первого и второго графов.

Пример. Граф A = {1->2, 1->6, 4->5, 5->1, 3->3}. Граф B = {3->4, 3->5, 1->2, 2->3, 6->6}
PathsA (maximal non-branching paths of A): 1->2, 1->6, 4->5->1, 3->3
PathsB (maximal non-branching paths of B): 3->4, 3->5, 1->2->3, 6->6
Соответствие вершин: 1(A):3(B), 2(A):4(B), 6(A):5(B), 4(A):1(B), 5(A):2(B), 3(A):6(B).

Таким образом, задачу проверки изоморфизма двух графов можно решить нахождением таких соответствующих друг другу путей и, затем, проверкой равенства друг другу матриц смежности, построенных исходя их сохранения порядка вершин в полученных последовательностях путей (при этом каждая вершина добавляется в порядок следования единожды, при ее первом «упоминании»). В нашем примере для построения матриц смежности будут использоваться следующие порядки вершин:

A: 1, 2, 6, 4, 5, 3
B: 3, 4, 5, 1, 2, 6

Матрица смежности для A для заданного порядка вершин:



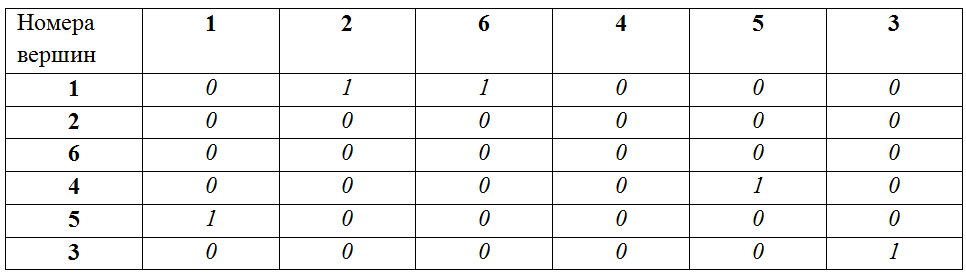
Матрица смежности для B для заданного порядка вершин:



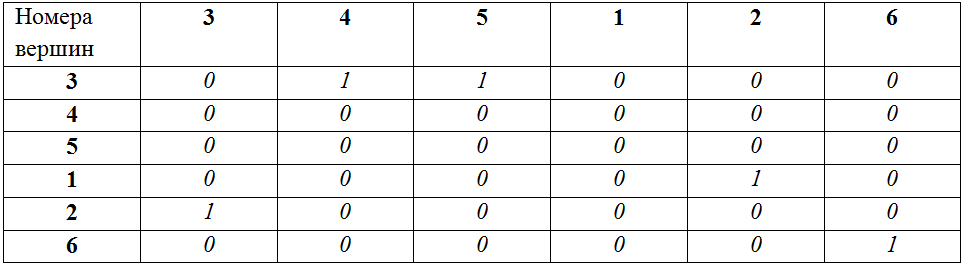
Матрицы равны, следовательно, графы A и B – изоморфны.

При этом данный подход (1) применим как для ориентированных, так и неориентированных графов, (2) применим для графов, содержащих более одной компоненты связности/ сильной связности, (3) применим для графов, содержащих кратные (множественные) ребра и петли, однако (4) не учитывает вершины, для которых отсутствуют инцидентные им ребра.

3. Ну хорошо, проверили изоморфизм графов. А что же с поиском подграфов?

А тут, честно признаюсь, все значительно сложнее. Тут у нас будет следующее ограничение: исходя из самой сути метода можно находить не любые, но лишь «вписанные» подграфы. А «вписанным» подграфом графа A мы будем называть такой его подграф, который может быть «приклеен» к другим частям графа A только за счет ребер, инцидентных лишь граничным вершинам его (подграфа) неразветвляющихся путей максимальной длины (при этом граф A может содержать и иные компоненты связности). Не волнуйтесь, ниже будет пример, и все будет понятней.

Кроме того, при решении данной задачи, помимо поиска соответствий NB-путей графов A и B по длине (как это было в рассмотренном выше примере с проверкой изоморфизма), также необходимо отдельно искать и следующие возможные соответствия между ними:

• Соответствия NB-путей – простых цепей из графа B NB-путям – простым цепям/ простым из циклам графа A. При этом изначально такие пути в графе A могут быть длиннее – в этом случае берутся их отрезки, равные по длине искомому пути из B.
• Соответствия NB-«концевых» путей графа B каким-либо NB-путям графа A (при этом пути из графа A также могут быть длиннее – в этом случае берутся их отрезки, равные по длине искомому пути из графа B).

Разберемся на примере:



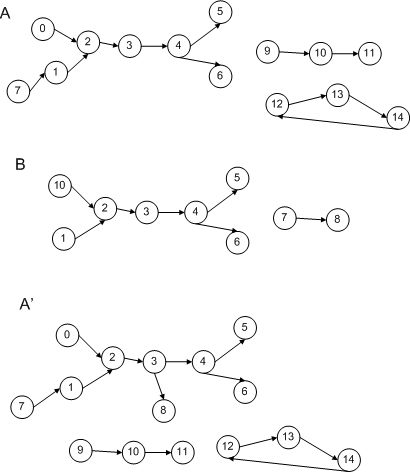
При поиске «вписанного» изоморфного подграфа графа B в графе A (см. рис. выше) будут обнаружены следующие соответствия:

• внутренний путь 2->3->4 графа B: внутренний путь 2->3->4 графа A,
• концевые пути 1->2 и 10->2 графа B: концевой путь 0->2 графа A и фрагмент концевого пути 7->1->2 графа A, а именно 1->2,
• простая цепь 7->8 графа B: отрезки простой цепи 9->10->11 графа A, а именно 9->10 и 10->11, а также отрезки простого цикла 12->13->14->12 графа A, а именно 12->13, 13->14, и 14->12.

Таким образом, в качестве «изоморфных графу B «вписанных» подграфов графа A могут быть найдены следующие 5 вариантов:

A1 = {0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 9->10}
A2 = {0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 10->11}
A3 = {0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 12->13}
A4 = {0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 13->14}
A5 = {0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 14->12}

Однако, если мы добавим к графу A дополнительное ребро 3->8, у нас получится граф A’ (ниже на том же рисунке). И в A’ уже будет не найти «вписанных» подграфов, изоморфных графу B. Действительно: ребро 3->8 «разбивает» путь 2->3->4 графа A на два и, значит, путей-кандидатов для внутреннего пути 2->3->4 графа B обнаружено не будет.

4. Теперь сам алгоритм

Теперь мы можем перейти к более детальному рассмотрению алгоритма поиска «вписанных» в граф А подграфов, изоморфных некоторому графу B.

Итак, алгоритм будет состоять из 4-х этапов:

• Препроцессинг,
• Сопоставление,
• Прореживание,
• Заключение.

Этап I. Препроцессинг

На данном этапе мы находим все NB-пути по каждому из графов, а также оцениваем факторы, ограничивающие пространство выбора при переборе. Т.е. мы делаем следующее:

1. Находим все NB-пути в графе A и заносим их в динамический массив (в С++ – в вектор) PathsA
2. Находим все NB-пути в графе B и заносим их в динамический массив (вектор) PathsB
3. Вычисляем и запоминаем кратность всех ребер графов A и B. Дальнейшие действия по этапам II-IV проводятся исходя из допущения, что кратности всех ребер равны 1. Однако на финальной стадии производится сравнение кратности ребер подграфа графа A-кандидата на изоморорфизм с графом B и кратности ребер самого графа B: все ребра подходящего графа-кандидата должны иметь кратность не меньшую, чем сопоставляемое им ребро графа B.
4. Подсчитываем степени всех вершин графов A и B (для ориентированных графов степени по входящим и исходящим ребрам учитываются отдельно).
5. Вычисляем матрицы кратчайших путей между каждой парой вершин в A и в B: назовем их DA и DB соответственно.
6. Формируем матрицу смежности – назовем ее B00 – для графа B таким же образом, как мы это делали выше, когда проверяли изоморфизм двух графов.

Итак, у нас есть NB-пути по обоим графам и параметры-ограничители из п.п. 3-5.

Этап II. Сопоставление

На данном этапе мы будем подбирать NB-пути-кандидаты (далее – просто «пути-кандидаты») из графа A для каждого из NB-путей графа B. Отметка о каждом пути-кандидате из PathsA для каждого i-го пути PathsB[i] будет записываться в двумерный динамический массив (в C++ – в вектор векторов) NPaths – соответственно в i-й вектор (i-ю строку) – в виде упорядоченного триплета чисел: номер соответствующего пути в PathsA – номер стартовой позиции в нем – длина пути.

Например, PathsB[2] = {1, 0, 3, 3, 1, 3} означает, что пути PathsB[2] сопоставлено 2 пути-кандидата из A: из PathsA[1] – 3 первых элемента пути начиная с нулевого (начального), и из PathsA[3] – также 3 элемента начиная с первого (следующего за начальным).

При этом поиск (подбор) путей-кандидатов мы будем производить по 4-м направлениям:

1. Поиск путей-кандидатов для всех внутренних NB-путей графа B из PathsB, т.е. тех, обе граничных вершины которых соединены в графе B как минимум с 2-мя другими вершинами (независимо от направления такой связи) и при этом такой путь не является простым циклом (ориентированным – для ориентированных графов).
2. Поиск путей-кандидатов для концевых NB-путей из PathsB.
3. Поиск путей-кандидатов для NB-путей – простых циклов из PathsB.
4. Поиск путей-кандидатов для NB-путей – простых цепей из PathsB.

При отборе путей-кандидатов для каждого i-го пути из PathsB сравниваются (вот тут-то нам и начинают пригождаться некоторые из вычисленных ранее параметров-ограничителей):

• его длина и длина пути-кандидата (должны быть равны для случаев 1 и 3, а для случаев 2 и 4 путь-кандидат из PathsA также может быть длиннее),
• степени его граничных вершин и соответствующих им вершин пути-кандидата (у вершин из пути-кандидата данные значения должны быть не менее чем у пути из PathsB).

Если по результатам этапа II для какого-либо из путей в PathsB не найдено ни одного пути-кандидата из PathsA, то считается, что A не содержит «вписанных» подграфов, изоморфных графу B.

Предварительное прореживание

Теперь давайте попробуем «ужать» граф A. Оставим в нем лишь те ребра, которые вошли в найденные нами пути-кандидаты. Если при этом граф A потерял хоть бы одно ребро по сравнению с его изначальным состоянием – возвращаемся на этап I “Препроцессинг”: степени вершин графа A и, соответственно, перечень путей-кандидатов может быть уменьшен и, соответственно, может быть сокращено пространство поиска.

Этап III. Прореживание перечня путей-кандидатов

Целью настоящего этапа является дальнейшее максимально возможное исключение неподходящих путей кандидатов. Для этого осуществим следующие действия.

1. Исключение заведомо неподходящих путей-кандидатов исходя из минимальных расстояний между вершинами в графе B. Исключению подлежит тот путь-кандидат по каждому PathsB[i], для которого хотя бы по одному PathsB[j] не нашлось ни одного такого пути-кандидата, чтобы кратчайшие расстояния между их граничными вершинами в графе A было меньше или равно кратчайшему расстоянию между соответствующими им граничными вершинами путей PathsB[i] и PathsB[j] из графа B.
2. Исключение для всех циклов из PathsB сопоставленных им нециклических путей-кандидатов и наоборот.
3. Аналогичное п. 1 исключение путей-кандидатов, но не по критерию кратчайшего расстояния между граничными вершинами, а их (граничных вершин) взаимному равенству либо неравенству.

Например, если:

• начальный элемент пути PathsB[i] не равен начальному элементу пути PathsB[j], и
• конечный элемент пути PathsB[i] не равен конечному элементу пути PathsB[j], и
• начальный элемент пути PathsB[i] равен конечному элементу пути PathsB[j], и
• начальный элемент пути PathsB[j] не равен конечному элементу пути PathsB[i],

то исключению подлежит тот путь-кандидат по пути PathsB[i], для которого хотя бы по одному PathsB[j] не нашлось ни одного пути-кандидата, удовлетворяющего приведенному выше условию относительно равенства/ неравенства соответственно их (путей-кандидатов) начальных и конечных вершин.

Т.е., грубо говоря, мы выкидываем те пути-кандидаты, которые заведомо не войдут в искомые подграфы – исходя из расстояния до всех прочих путей-кандидатов (страшно далеки эти пути от всех прочих), исходя из их цикличности/ нецикличности, а также исходя из должного равенства/ неравенства их граничных вершин с граничными вершинами других путей-кандидатов.

Если по результатам этапа III хотя бы 1 путь-кандидат был удален из PathsA, то – опять же – обновляется граф А – в нем остаются только те ребра, которые вошли в оставшиеся пути-кандидаты. И, опять же, если при этом граф A «похудел» хотя бы на одно ребро – снова возвращаемся на этап I “Препроцессинг”: степени вершин графа A и, соответственно, перечень путей-кандидатов может быть уменьшен и, соответственно, может быть сокращено пространство поиска.

Этап IV. Заключение

Каждое возможное сочетания всех оставшихся путей-кандидатов задает подграф графа A. Для каждого такого подграфа строится матрица смежности с учетом порядка следования путей кандидатов таким же образом, как была построена матрица смежности B00 для графа B, а затем эти матрицы смежности сравниваются между собой.

Если они равны, то сравниваются кратности ребер (см. п. 3 Этапа I Препроцессинг). Если все эти условия выполнены – найденный подграф считается изоморфным графу B и добавляется в множество найденных результатов.

При проведении этапа IV “Заключение” возможно применение различных дополнительных проверок, ускоряющих выявление и отбрасывание неподходящего подграфа.

5. Как все запутано… Рассмотрим пример работы алгоритма

Не знаю как Вам, а мне без примера было бы непонятно. Давайте рассмотрим все на примере.

На рис. ниже приведены графы A = {1->2, 2->5, 5->15, 16->15, 5->5, 5->5, 5->4, 5->6, 7->6, 6->8, 6->6, 6->9, 9->10, 9->11, 12->0, 0->12, 4->13, 13->14, 14->4} и B = {1->1, 4->5, 5->1, 1->3, 3->3, 3->2, 2->7, 2->8, 9->10, 10->9, 1->6, 6->11, 11->12, 12->6}. Нашей задачей является нахождение в графе A всех «вписанных» подграфов, изоморфных графу B. Результат также отражен на рисунке: найденные вершины и ребра графа A выделены толстой линией, а номера соответствующих вершин графа B указаны в скобках (если вариантов несколько – они указываются через дробь).



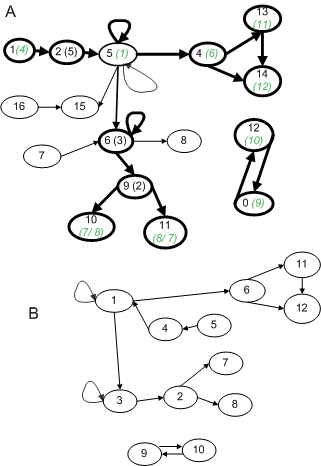
При решении задачи поиска в графе A «вписанных» подграфов, изоморфных графу B, имеем следующие результаты работы алгоритма.

Этап I: Выполнены все действия и расчеты по п.п. 1-5 данного этапа, ниже приводятся полученные PathsA и PathsB.

PathsA:

1->2->5
4->13->14 4
5->4
5->5
5->6
5->15
6->6
6->8
6->9
7->6
9->10
9->11
16->15
0->12->0

PathsB:

1->1
1->3
1->6
2->7
2->8
3->2
3->3
4->5->1
6->11->12->6
9->10->9

Этапы II-III. Сопоставление показало, что для каждого пути из PathsA находится как минимум один путь-кандидат из PathsB, а по результатам предварительного прореживания PathsA был сокращен. На этапе основного прореживания (III) дальнейшего сокращения PathsA не произошло. В результате PathsA и PathsB приняли вид:

PathsA:

1->2->5
4->13->14->4
5->4
5->5
5->6
6->6
6->9
9->10
9->11
0->12->0

PathsB:

1->1
1->3
1->6
2->7
2->8
3->2
3->3
4->5->1
6->11->12->6
9->10->9

Итоговое сопоставление NPaths имеет вид:
NPaths:

i=0: 3 0 2
i=1: 4 0 2
i=2: 2 0 2
i=3: 7 0 2 8 0 2
i=4: 7 0 2 8 0 2
i=5: 6 0 2
i=6: 5 0 2
i=7: 0 0 3
i=8: 1 0 4
i=9: 9 0 3

Здесь самое время вспомнить, что каждый упорядоченный триплет чисел в NPaths[i] задает соответствующий PathsB[i] путь-кандидат из A в формате: номер соответствующего пути из PathsA – стартовая позиция отрезка из данного пути – длина отрезка. Таким образом, нетрудно убедиться, что пути PathsB[0] = {1->1} (i=0: 3 0 2) соответствует единственный путь из A, а именно: отрезок из пути PathsA[3], начинающийся с его самого начала и имеющий длину 2.

Этап IV. В результате в графе A был найден единственный подграф A1, изоморфный графу B. A1 = {0->12, 1->2, 2->5, 4->13, 5->4, 5->5, 5->6, 6->6, 6->9, 9->10, 9->11, 12->0, 13->14, 14->4}.

5. Что же дальше?

А, дальше, в принципе, и все. Хотя не совсем: автор должен признаться, что алгоритм может еще дорабатываться и дорабатываться. Что тут нужно добавить?

1. При введении дополнительных признаков вершин графов A и B (например, при задании графами химических соединений каждой вершине может быть сопоставлен числовой код, соответствующий одному и только одному атому (изотопу)) процесс поиска может быть ускорен за счет большей точности сопоставлений по Этапу II: дополнительным условием отбора путей-кандидатов будет соответствие меток вершин.
2. Скорость работы представленного алгоритма очень сильно зависит от структур исходных графов и их взаимного соответствия. Алгоритм будет работать тем быстрее, чем более «уникальную», «нестандартную» и несимметричную структуру имеет граф-образец B.
3. Исходя из этого, одним из возможных путей использования представленного алгоритма может являться, в том числе, «скриннинговый» поиск решения по любому из направлений:
   (1) поиск именно «вписанных» подграфов, изоморфных данному,
   (2) проверка изоморфности двух различных графов.
   «Скрининг» здесь подразумевает «предварительный экспресс-поиск решения», для чего необходимо задать некоторое предельное время его работы, по истечении которого при отсутствии результата можно считать, что данная задача подлежит решению другим алгоритмом.
4. Возможно, для кого-то представленный алгоритм может оказаться полезным как при решении различных практических задач, так и при разработке новых алгоритмов решения задачи об изоморфном подграфе.

Литература

Общее по проблематике:
1. Bonnici, V., Giugno, R., Pulvirenti, A. et al. A subgraph isomorphism algorithm and its application to biochemical data. BMC Bioinformatics 14, S13 (2013). doi.org/10.1186/1471-2105-14-S7-S13.
2. Cordella L, Foggia P, Sansone C, Vento M: A (Sub)Graph Isomorphism Algorithm for Matching Large Graphs. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2004, 26 (10): 1367-1372. 10.1109/TPAMI.2004.75.
3. Ullmann Julian R.: An algorithm for Subgraph Isomorphism. Journal of the Association for Computing Machinery. 1976, 23: 31-42. 10.1145/321921.321925.
4. Ullmann Julian R.: Bit-vector algorithms for binary constraint satisfaction and subgraph isomorphism. J Exp Algorithmics. 2011, 15 (1.6): 1.1-1.6. 1.64

Написанный более официальным языком препринт автора про это самый «алгоритм на основе анализа NB-Paths», содержащий также инфу о предпринятой попытке его реализации на C++:
5. Черноухов С.А. 2020. Preprints.RU. Проверка изоморфности двух графов и поиск изоморфных «вписанных» подграфов: подход, основанный на анализе максимально протяженных неразветвляющихся путей / Maximal non-branching paths approach to solve (sub)graph isomorphism problem. DOI: dx.doi.org/10.24108/preprints-3111977

Полезные интернет-источники по теме:
6. coderoad.ru/17480142/Есть-ли-простой-пример-для-объяснения-алгоритма-Ульмана
7. issue.life/questions/8176298.