Если вы когда-нибудь прослушивали музыку через наушники и через колонки, то наверняка обращали внимание, что звучит она по-разному. В наушниках часто возникает ощущение, что источник звука находится где-то внутри головы. Бывают и другие негативные эффекты: некоторые старые записи сделаны так, что, например, гитара полностью смикширована в левый канал, а ударные - в правый. На колонках это звучит нормально - как будто гитарист стоит примерно там где один из громкоговорителей, но в наушниках - это весьма неприятно, потому что неестественно: в природе не бывает такого, чтобы звук слышало только одно ухо.

Скажу больше: подавляющее большинство коммерческих аудиозаписей рассчитаны именно на прослушивание через колонки. То есть звукорежиссёр при подготовке записи делает всё, чтобы она правильно (в соответствии с задумками автора) звучала в студийных мониторах, а как оно будет в наушниках - с большой вероятностью даже не проверит.

Казалось бы, если нравится - всегда можно слушать через колонки. Но увы, бывают ограничения: хочется послушать музыку в офисе, в транспорте, да или просто поздно вечером, когда дети/родители/соседи уже давно спят. Кроме того, стоимость качественных акустических систем в разы превышает стоимость качественных наушников. А есть ещё может понадобиться отдельный усилитель, акустическая обработка комнаты и т. д. Иногда колонки просто негде разместить в квартире... С наушниками всё проще.

Что делать?

Одну минуточку! Но ведь когда мы слушаем музыку через колонки (или вообще сидим в концертном зале), каждого уха достигает совершенно определённый акустический сигнал. Значит если записать этот сигнал с помощью маленького микрофона, расположенного внутри каждой ушной раковины, и потом воспроизвести через хорошие наушники, то мы получим то же самое ощущение присутствия в зале. Разве что за исключением низкочастотных сигналов, ощущаемых грудной клеткой. Впрочем, это слишком сложная процедура, хотя такие записи (их называют бинауральными) иногда делают, и даже продают.

А что если воспроизвести через колонки какой-то тестовый сигнал, записать его этими самыми крошечными микрофонами в ушах, определить, как сигнал преобразовался, и потом аналогичным образом преобразовывать любимую музыку перед проигрыванием через наушники?

HRTF и HRIR

Представьте себе, что у вас есть только одна колонка, и она стоит, допустим, справа от вашего монитора. Подадим на неё короткий импульс. Излучаемый акустический сигнал обозначим как x(t). Тогда Вашего правого уха соответствующая акустическая волна достигнет чуть раньше, чем левого. Кроме того, от левого уха колонку будет заслонять ваша голова, в результате туда попадёт чуть более "глухой" и более тихий звук. На самом деле, до правого уха этот звук тоже не дойдёт неизменным: помимо прямого сигнала, будет ещё сигнал, отражённый от виска, от ушной раковины и т. д. Об отражениях от монитора, стола, стен, потолка, пола и мебели говорить пока не будем, представим себе, что их нет. Обозначим сигнал, принятый левым ухом, как X_L(t), а правым ухом - X_R(t). Эти сигналы можно представить как исходный сигнал, преобразованный двумя разными функциями: X_L(t)=F_L(x(t)) и X_R(t)=F_R(x(t)).

Подобные преобразования, вносимые в акустический сигнал можно описывать по-разному - можно нарисовать амплитудно-частотную и фазо-частотную характеристики, можно расписать передаточную функцию в виде многочленов, а можно задать импульсную характеристику и описать это преобразование как операцию свёртки (обозначим её символом *), тогда:

X_L(t) = h_L(t) * x(t) и X_R(t) = h_R(t) * x(t),

где h_L(t) и h_R(t) - импульсная характеристика фильтров соответственно для левого и правого уха.

Но как узнать вид этих передаточных функции или импульсных характеристик? К счастью, это уже было сделано (и не один раз). Например, в 2003-м году в институте IRCAM (Франция) были обследованы несколько десятков человек. Каждого из них сажали на стул в специальной акустической безэховой камере, устанавливали в уши крошечные микрофоны, а дальше воспроизводили тестовые сигналы с помощью небольшого, но сравнительно качественного студийного монитора, закреплённого на специальном сервоприводе так, чтобы можно было перемещать его в двух плоскостях, сохраняя неизменным расстояние до слушателя. Таким образом звук приходил к голове испытуемого под разными углами. Записанные сигналы обрабатывались, производилась коррекция для исключения неидеальности характеристик микрофонов и акустической системы. В результате для каждого человека было получено почти по две сотни импульсных характеристик. Их называют Head-Related Impulse Response - импульсная характеристика относительно головы. В литературе чаще встречается термин HRTF, это почти то же самое.

Казалось бы, задача решена. Ищем в базе данных IRCAM импульсную характеристику, снятую на уровне глаз с азимута, скажем, 30 градусов, всю прослушиваемую музыку пропускаем через соответствующий FIR-фильтр и подаём на хорошие наушники с плоской АЧХ. К сожалению, всё несколько сложнее…

Реальные наушники

В мире есть пара десятков крупных брендов, предлагающих качественные головные телефоны - Sennheizer, AKG, Beyerdynamic, Sony и т. д. Многие из них занимаются этим бизнесом не один десяток лет и придерживаются определённых традиций. Одна из них - фонограмма должна звучать в наушниках аналогично колонкам: никакие частоты не должны "выпячиваться" или "проваливаться" по сравнению с прослушиванием аналогичной фонограммы на качественных акустических системах с плоской АЧХ. Проблема в том, что для этого приходится делать наушники с кривой АЧХ. Например, часто в качестве оптимальной АЧХ наушников принимают одну из семейства кривых "Harman Target Curves". Таким образом, фактически, производители наушников уже давно и достаточно успешно рещают задачу имитации "прямой" импульсной характеристики, то есть звук из правой колонки воспринимается также, как звук из правого наушника. "Обратный" звук - такой, который попадает из правой колонки в левое ухо, в обычных наушниках отсутствует. Именно его нам и нужно сформировать, обладая знанием об HRTF.

На самом деле, помимо имитации "прямой" HRTF осуществляется ещё и некая стандартная эквализация, но об этом поговорим как-нибудь в другой раз.

Немного рассуждений

Если вы прониклись концепцией, но зеваете при виде формул - можете пропустить этот раздел.

Итак, у нас есть комплект импульсных характеристик: h_R(t) и h_L(t). Мы предполагаем, что "прямая" HRTF (то есть h_R(t) в нашем примере) имитируется за счёт конструкции головных телефонов, иначе говоря, наушники производят преобразование вида F_R(), то есть делают свёртку сигнала с h_R(t). Теперь нам нужно придумать фильтр, который сделает так, чтобы в левое ухо попал сигнал X_L(t) - как если бы мы слушали колонки. Обозначим импульсную характеристику этого фильтр как h_corr(t). Должно выполняться равенство: h_corr(t)*h_R(t)*x(t)=h_L(t)*x(t). Здесь появляется свёртка с h_R(t), так как левый наушник имеет точно такую же конструкцию как правый и преобразует сигнал точно также. Сократим лишнее (со свёрткой так можно): h_corr(t)*h_R(t)=h_L(t).

У меня в институте не было курса по цифровой обработке сигналов, но о преобразовании Фурье нам, конечно, рассказывали в рамках курса мат. анализа. Поэтому я помню, что преобразование Фурье - это фактически переход из временной области в частотную, а свёртка во временной области эквивалентна умножению в частотной области. Обозначим преобразование Фурье как fft(). Тогда:
fft(h_corr(t)) ? fft(h_R(t)) = fft(h_L(t))
(символом ? обозначаем поэлементное умножение).
Тут здорово то, что в частотной области не возбраняется не только поэлементное умножение, но и деление:
fft(h_corr(t)) = fft(h_L(t)) / fft(h_R(t)).

Дальше остаётся перейти снова во временную область (выполнить обратное преобразование Фурье), и мы получаем импульсную характеристику необходимого нам фильтра!

Если углубиться в теорию, то выяснится, что такой фокус - перейти в частотную область, поделить и перейти обратно во временную область - не всегда возможен. Забегая вперёд скажу: в данном случае возможен.

Для полноты картины нужно отметить, что в итоге нужно к сигналу, подаваемому в левый наушник прибавить сигнал правого канала, пропущенный через найденный нами фильтр, а к сигналу, подаваемому в правый наушник прибавить сигнал левого канала, также пропущенный через этот фильтр.

Я считаю, что нахождение фильтра, определяющего именно разность между сигналами для каждого из ушей концептуально более правильно, чем раздельное преобразование сигналов для правого и левого уха. Ведь мозг ничего не знает об истинном характере звука в пространстве. Он воспринимает только сигналы от обоих ушей, и по разнице между этими сигналами пытается определить направление на источник звука.

Второй важный момент: для локализации звука (то есть определения направления) не имеет особого значения АЧХ самих наушников (как и их "target curve") - она сократилась в наших уравнениях. Однако, необходимо, чтобы левый и правый наушники были максимально похожи. Поэтому, никто не мешает до или после данного фильтра использовать обычную эквализацию, чтобы получить именно такой спектр звука, какой нам хочется. Заодно можно компенсировать недостатки АЧХ наушников и/или недостатки записи.

О существующих решениях

Я не претендую на полный обзор, но кое-что перечислить всё-таки нужно. Во-первых есть много плагинов для разных программных аудио-плееров и редакторов, осуществляющих так называемый cross-feed. Подавляющее большинство из них - просто подмешивают звук противоположного канала. Иногда слегка его фильтруют и/или добавляют задержку. К сожалению. я не нашёл ни одного плагина такого типа, позволяющего сформировать звуковую картину, аналогичную прослушиванию на хороших колонках, когда можно с закрытыми глазами показать, где "находится" каждый из исполнителей. Возможно, причина в том, что у меня не самая типичная голова - значительно шире среднестатистической (замучился выбирать велосипедный шлем для катания зимой).

Единственный готовый инструмент из тех, что я пробовал, обеспечивший хорошую локализацию в пространстве - Dolby Headphones. Существует плагин-обёртка для известного в узких кругах аудиоплеера foobar2000, позволяющая обрабатывать звук соответствующей библиотекой от Dolby. Но у неё есть два недостатка. Во-первых, она искажает АЧХ. Есть подозрение, что она рассчитана именно на наушники с ровной АЧХ (как в рассуждениях выше). Это можно выправлять эквалайзером, но как-то неаккуратненько. Второй недостаток - сомнительная легальность. Наверное, можно купить программный пакет, в который входит эта библиотека от Dolby, но не знаю, насколько будет правомерно использовать её отдельно. Также есть очевидные сложности с использованием на ОС, отличных от Windows. Можно, конечно, снять импульсные характеристики, и использовать их, но это уже reverse-engineering, что тоже не всегда легально.

Разбираемся в нюансах и кодим

Если хочется наконец попробовать, и лень читать все эти буквы - в конце есть ссылка на GitHub, но лучше всё-таки прочитать, т. к. комментариев в коде немного, а readme.md я пока не написал.

Традиционно подобные фильтры часто делают в Matlab. Я никогда раньше с ним не работал, но решил повозиться с открытым аналогом - GNU Octave. Итак, за дело.

Для начала посмотрим, как выглядят импульсы от IRCAM. Виртуальные колонки у меня будут стоять под углом +-30 градусов - это классическая расстановка, когда колонки и слушатель образуют равносторонний треугольник. Вначале был соблазн взять единственный стерео-файл, в котором записаны сигналы для правого и левого уха, но оказалось, что импульсы правого и левого каналов могут ощутимо различаться (вероятно, вследствие асимметрии головы у большинства людей), поэтому стоит брать один и тот же канал, например, левый и файлы, снятые под разными углами. Я после ряда проб и ошибок выбрал файлы IRC_1006_R_R0195_T030_P000.wav и IRC_1006_R_R0195_T330_P000.wav, но, повторюсь, у меня не самая типичная голова, поэтому Вам с большой вероятностью лучше подойдёт какая-нибудь другая пара импульсов.

Здесь 1006 - идентификатор испытуемого, 0195 - расстояние от громкоговорителя до головы в сантиметрах, 030/330 - азимут (0 - колонка ровно перед слушателем, 90 слева, 180 - сзади, 270 - справа), 000 - нулевой угол над горизонтом. Также на сайте IRCAM доступны xml-файлы с описанием испытуемых - рост, расстояние между ушами, длина волос, размер ушных раковин и т. п. Посмотрим как выглядят эти импульсы.

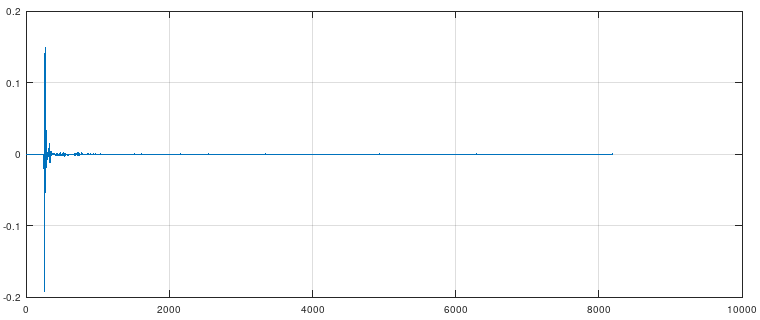
Длина импульсов составляет 8192 сэмпла, при частоте дискретизации 44.1кГц. Получается 186мс, что соответствует длине волны 63м. Очевидно, что длина сильно избыточна, поскольку при такой длине волны (на 2 с лишним порядка больше размера головы!) никакого стереоэффекта нет, и оба уха слышат идентичный сигнал. Поэтому при загрузке файлов их можно сразу обрезать до 1024..4096 семплов. Например так:

channel_idx = 1; % Channel index, used from input files: 1 - left, 2 - right
max_impulse_len = 4096;
[impulse, fs] = audioread(fname);
len = min(rows(impulse), max_impulse_len);

Данные ненужного канала тоже выкинем.

impulse = impulse(1 : len, channel_idx);

Далее проведём наши вычисления на основе быстрого преобразования Фурье:

fft_div = fft(impulse_opposite) ./ fft(impulse_direct);
impulse_tf = real(ifft(fft_div));

По-умному это называется deconvolution или system identification (т. к. позволяет определить свойства системы на основе входного и выходного сигналов). Посмотрим, что получается:

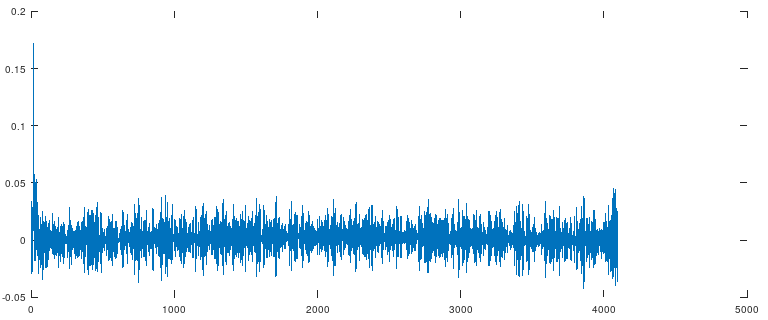
Что-то получилось :) Скажу больше, оно в целом даже работает как ожидалось. Однако, отношение сигнал-шум в этом импульсе не радует глаз. Перфекционист внутри меня негодует... Можно провести свёртку, и проверить, что h_corr(t) * h_R(t) = h_L(t).
Посмотрим, как будет выглядеть "сигнал ошибки":

plot(conv(impulsedirect, impulsetf)(1:4096) - impulseopposite);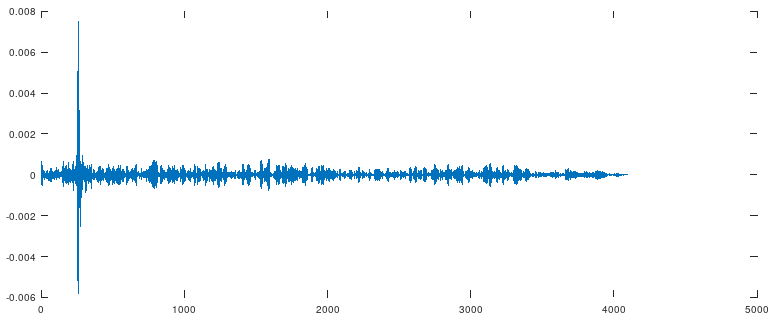

Не скажу, что идеально, ошибка порядка нескольких процентов. Видимо не всё так просто...

Пришлось засесть за Гугл и найти учебники по цифровой обработке сигналов. Оказывается, проблема известна уже чуть ли не пол века: деконволюция через преобразование Фурье даёт большие ошибки. К счастью, более подходящие методы тоже давно известны. Один из классических - метод наименьших квадратов (МНК) с использованием матрицы Тёплица и её инверсией методом Дурбина-Левинсона. Было найдено несколько готовых реализаций для Matlab, из которых получилось сделать то, что хотелось (подробности здесь приводить не буду, если интересно - можно посмотреть на гитхабе).

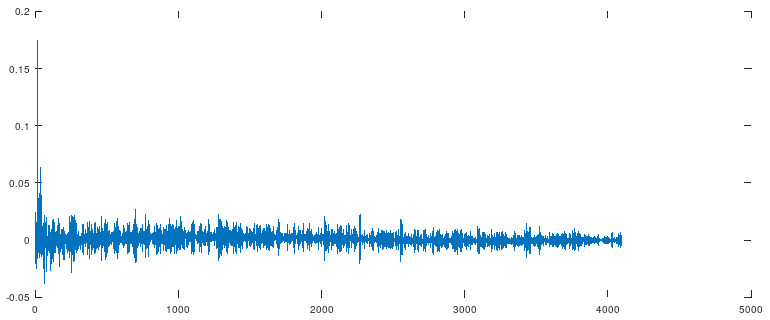
Сам импульс, полученный с помощью МНК:

И "сигнал ошибки":

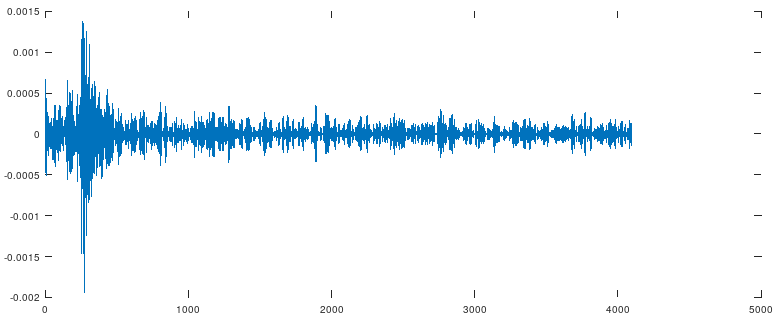
Теперь получше, ошибка около одного процента.

Попробуем увеличить масштаб картинки с полученным импульсом:

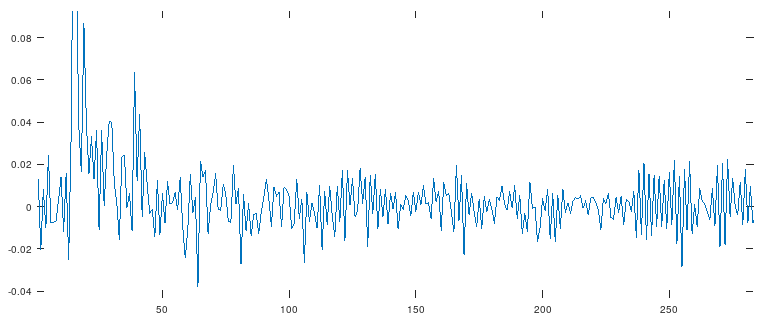
Мне кажется, в этом импульсе многовато высокочастотных составляющих. Что ж, попробуем обрезать всё, что выше 20кГц (за пределами диапазона слышимых частот) с помощью ФНЧ:

lpf = remez(2 * round(fs / 600), [0 20000 / (fs / 2) 21000 / (fs / 2) 1], [1 1 0 0]); % For Matlab environment change "remez" to "firpm". 
filteredImpulse=conv(impulse_tf, lpf, 'same');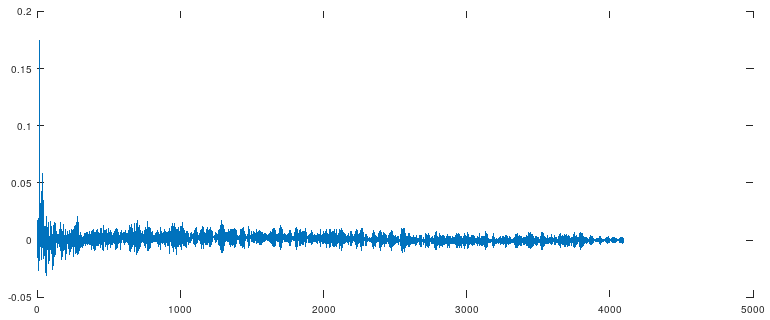

Выглядит ещё лучше.
Я слабо верю, что можно услышать разницу с использованием ФНЧ и без. На ресурсоёмкость это тоже не должно влиять. В общем, решение спорное, но я захотел сделать так.

Так, мы совсем забыли о длине… Мы же говорили, что 8192 сэмпла - это безумно большой запас, а сами сделали всего лишь вдвое меньше. Причём значительная часть энергии в импульсном отклике этого фильтра - банальный шум! Думаю, здесь стоит применить так называемую оконную функцию, например, функцию Блэкмана.

Честно говоря, я не стал выяснять, какая оконная функция здесь подходит лучше всего, но функция Блэкмана используется, например, в программе DRC, выполняющей похожую задачу, и я решил поступить также. Надеюсь, автор DRC посвятил этому вопросу больше времени :)
Не уверен, будет ли слышно разницу, но перфекционизм...

Сначала определим, где будет центр оконной функции. Для этого возьмём медиану группового времени задержки, которое даёт наш фильтр:

avgDelay = round(median(grpdelay(impulse_tf)));

Теперь сформируем собственно оконную функцию и поэлементно умножим на неё наш импульс.

wnd = window(@blackman, 2 * (size(impulse_tf)(1) - avgDelay));
% Cut the window in size
wnd = flipud(wnd(1:size(impulse_tf)));
% Apply window
impulse_tf = impulse_tf .* wnd;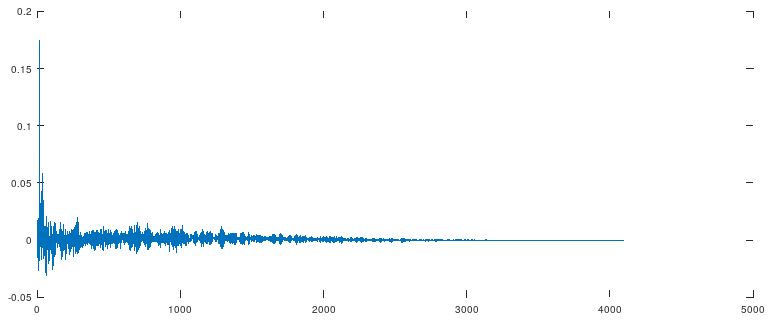

Неплохо. Часть лишнего удалось убрать. Думаю, если уменьшить длину импульса ещё в 2..4 раза, то будет совсем красиво. Но тут надо оценивать на слух - я отчётливо слышал разницу в зависимости от длины импульса. Впрочем, это могли быть артефакты фильтрации на лету при прослушивании.

Дальше имеет смысл визуально сравнить полученный импульс после свёртки с исходным (примерно это мы делали при попытке использовать FFT). Я вывел на один график сами импульсы, и их же в частотной области, то есть после преобразования Фурье - отдельно модуль (то есть по сути АЧХ), действительную часть и мнимую часть:

Выглядит годно. Заметные отличия (и то если увеличить :)) - в области самых верхних частот, где мы собственно применили ФНЧ. То есть, похоже, что всё правильно.

Осталось сохранить полученный импульс в два стерео-файла, отличающихся только переменой правого и левого каналов.

impulse_tf_stereo_L(:, 2) = impulse_tf;
impulse_tf_stereo_L(1, 1) = 1;
impulse_tf_stereo_R(:, 1) = impulse_tf;
impulse_tf_stereo_R(1, 2) = 1;
audiowrite(strcat(directory, fname_direct, '_TF_stereo_L.wav'), impulse_tf_stereo_L, fs);
audiowrite(strcat(directory, fname_direct, '_TF_stereo_R.wav'), impulse_tf_stereo_R, fs);

Теперь осталось проверить, что собственно получилось. Для этого я использовал уже упоминавшийся аудиоплеер foobar2000 с плагином "Stereo Convolver". Настроен он у меня следующим образом:

Также рекомендую заняться эквализацией - значительных изменений тонального баланса от этого фильтра быть не должно, но тем не менее… Да и вообще, эквализация под свои вкусы никогда не помешает.

Если результат в плане пространственного разрешения фонограмм не понравился - можно попробовать выбрать другой импульс из базы IRCAM и попробовать снова. Либо закрыть эту страницу и заняться чем-нибудь более интересным.

Заключение

В общем, результаты этого хоббийного исследования меня удовлетворяют. Лучшего пространственного разрешения в наушниках я пока не слышал. Ну и заодно слегка подтянул знания в области цифровой обработки сигналов.

Есть и кое-какие мысли по дальнейшему развитию подхода.

Весь использованный код для GNU Octave выложен на GitHub.

Да, пара иллюстраций позаимствована с Википедии. Вроде бы лицензия это допускает.

Ссылки

• http://recherche.ircam.fr/equipes/salles/listen/ - база данных измеренных HRIR реальных людей. Измерения проведены институтом IRCAM (Франция) в 2003г. На страничке LINKS есть ссылки на другие измерения HRTF.

• https://ocw.mit.edu/courses/mechanical-engineering/2-161-signal-processing-continuous-and-discrete-fall-2008/lecture-notes/ - курс лекций MIT по цифровой обработке сигналов,

• https://www.musicdsp.org/en/latest/ - база знаний по синтезу и обработке музыкальных сигналов,

• https://en.wikipedia.org/wiki/Head-related_transfer_function - статья в Википедии о передаточных функциях человеческой головы.

• https://www.headphones.com/pages/measurements-and-frequency-response - об амплитудно-частотных характеристиках наушников.

• http://drc-fir.sourceforge.net/ - набор утилит для создания КИХ-фильтров, корректирующих искажения, вносимые акустикой комнаты.

• https://hydrogenaud.io/index.php?topic=90662.0 - плагин Stereo Convolver для foobar2000.