
Начну с банальности — никто не будет спорить с утверждением, что каждая научная проблема нуждается во всестороннем рассмотрении. Иногда очень помогает буквальное использование этого подхода — хорошо бы уметь построить модель исследуемого процесса и просто взглянуть на неё с разных сторон. Далее я попробую показать, как это работает в применении к исследованию динамических систем и связанных с ними объектов
Динамические системы и фазовые траектории
В предыдущей статье я попытался рассказать о своём приложении для исследования динамических систем, которые можно описать с помощью систем Обыкновенных Дифференциальных Уравнений (ОДУ). Это приложение ориентировано, прежде всего, на графический способ представления результатов и их визуальный анализ.
Динамическая система — это система, которая изменяется (эволюционирует) с течением времени, причем её состояние в определенный момент однозначно определяется начальным состоянием. Часто динамическую систему можно описать с помощью набора переменных, зависящих от времени. Для конкретной динамической системы обычно задаются начальные значения переменных, описывающих её, а также законы, по которым эти переменные изменяются. Часто такой закон имеет вид системы ОДУ, которая связывает скорость изменения переменных с их величинами.
,
где — переменные системы, — параметры, — производная по времени.
Для анализа поведения динамической системы можно использовать графики зависимостей переменных от времени. Например, динамическая система простого маятника, колеблющегося в одной плоскости, является двумерной (имеет размерность два), то есть описывается двумя переменными — отклонением маятника от вертикали и его скоростью. Отклонение и скорость — периодические функции от времени, и их графики имеют соответствующий вид.
Одним из важных видов представления динамической системы является ее фазовая траектория — кривая в пространстве всех возможных состояний, описывающая эволюцию системы, начиная от начального её положения. Для системы с двумя переменными это двумерная кривая, для периодических колебаний простого маятника эта кривая замкнутая, поскольку время от времени система возвращается в своё первоначальное состояние. Для системы с тремя переменными её фазовая траектория — это уже кривая в трехмерном пространстве (нужно заметить, что именно начиная с размерности три динамические системы, представляемые с помощью систем ОДУ, демонстрируют различные интересные типы поведения, в частности, хаотическое). Для изображения кривой в трехмерном пространстве естественно использовать проволочную модель.
Много ли проволоки расходуется на создание проволочной модели?
Проволочная (или каркасная) модель — это просто изображение трехмерного объекта, состоящее только из рёбер, то есть объектов одномерных. На экране компьютера проволочная модель состоит из отрезков прямых и кривых, формирующих как бы объемное изображение. Поскольку экран плоский и на нём мы видим лишь проекцию изображения на плоскость, объемность проволочной модели не всегда очевидна, поэтому необходимо применять различные способы передачи глубины изображения. Например, можно использовать перспективную проекцию (при которой более далекие от наблюдателя рёбра имеют относительно меньший размер, чем более близкие), или отобразить дальние рёбра при помощи специальных оттенков или цветов (скажем, более тусклых). Самый же простой способ придать проволочной модели объемность — это подвергнуть её интерактивному вращению, то есть дать пользователю возможность рассматривать модель как бы с разных сторон. Для просмотра трехмерных фазовых траекторий в приложении, предназначенном для исследования динамических систем, мне понадобилось написать просмотрщик (viewer — вьюер) проволочных моделей.

Идею такого вьюера я позаимствовал из одной очень древней программы 90-ых годов, она называлась 3DViewer, её автор — Oscar Garcia (garciao@mof.govt.nz, 1 Clyde St, Rotorua, New Zealand). Эта программа позволяла просматривать проволочные модели, заданные в виде текстовых файлов очень простой структуры: в начале файла в отдельных строках указываются точки всех вершин, формирующих рёбра (в виде трех вещественных координат), а затем задаются собственно рёбра (с помощью номеров вершин и кодов цветов, которыми рисуется соответствующее ребро). Мой вьюер работает значительно медленнее, чем оригинальный 3DViewer, тем не менее, он позволяет вращать модель, а также приближать и отдалять её. Для просмотра фазовой траектории нужно просто решить соответствующую систему ОДУ и сгенерировать текстовый файл для вьюера (кривая аппроксимируется с помощью множества отрезков прямых, они и являются рёбрами модели).
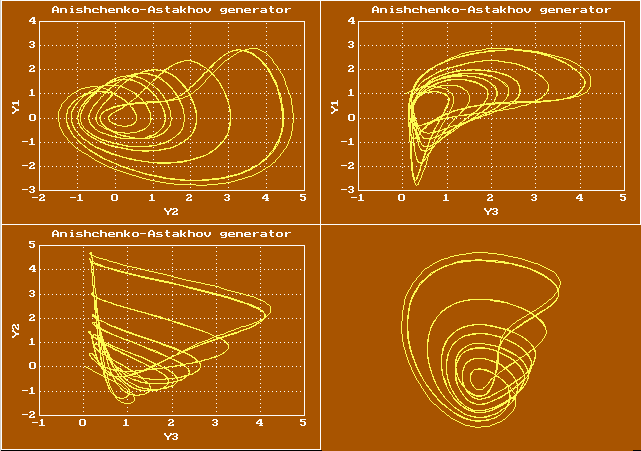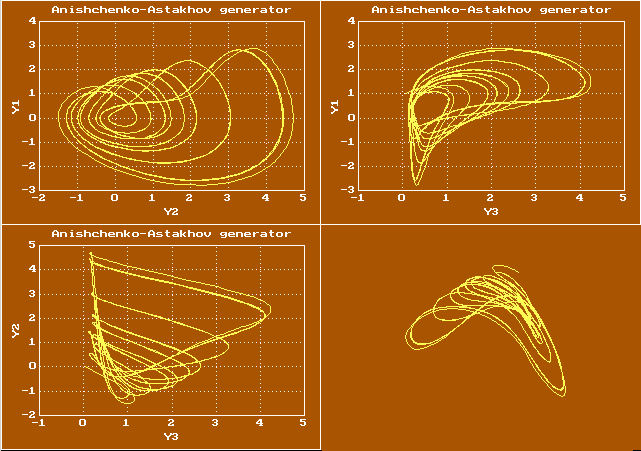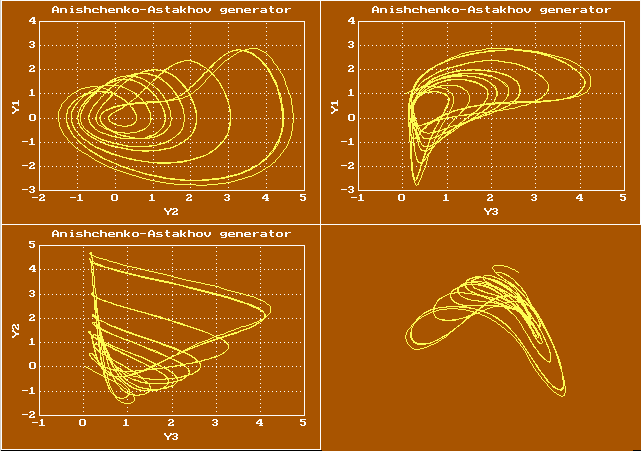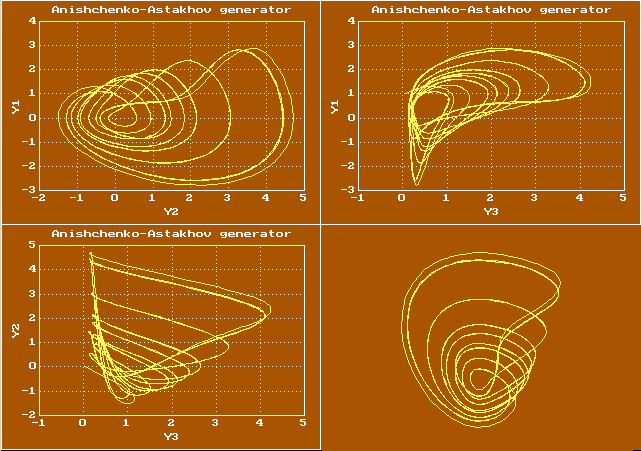
Для систем более чем третьего порядка фазовая траектория — это уже кривая в пространстве размерности больше, чем три, но её проекцию в трехмерное пространство все равно удобно рассматривать с помощью вьюера. Вот пример изображения фазовой траектории для системы Дадрас-Момени в виде её проекций на три координатных плоскости, а также вращаемой проволочной модели
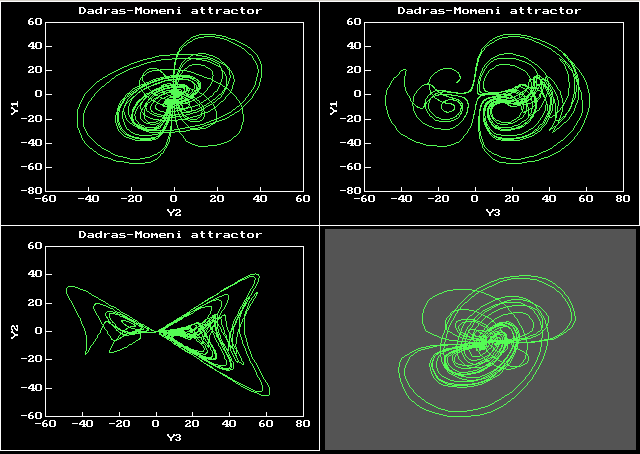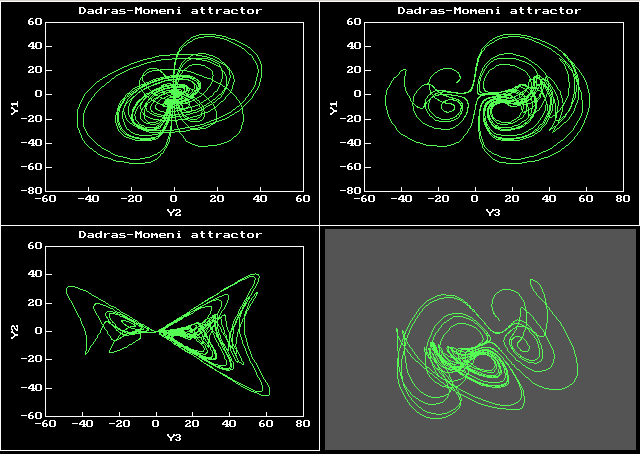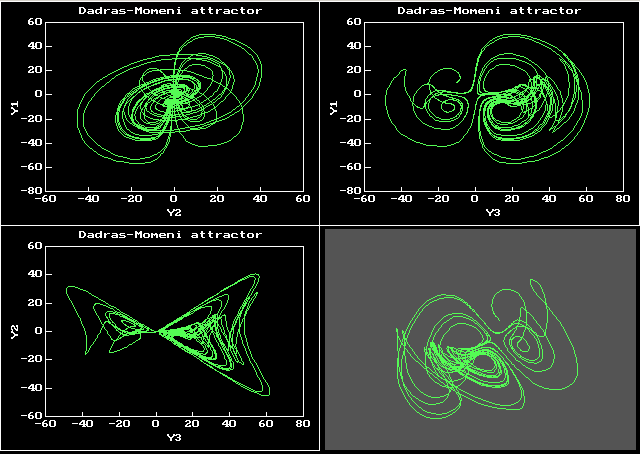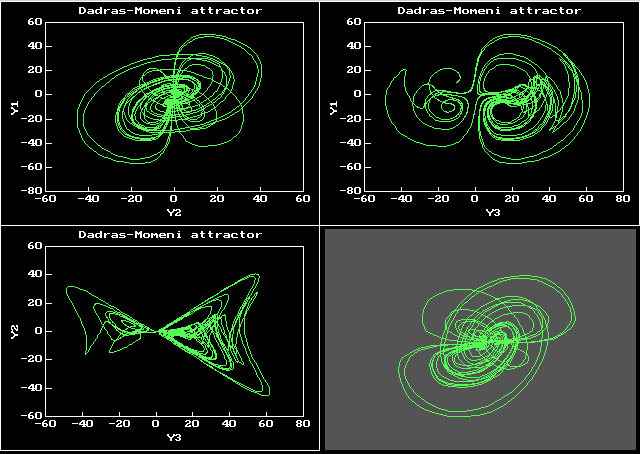
Ещё один пример проволочной модели для динамической системы
Проволочные модели для представления параметрических пространственных кривых
Помимо фазовых траекторий, с помощью вьюера проволочных моделей можно просматривать и любые трехмерные кривые, заданные в параметрическом виде
Заданная параметрическая кривая может быть фазовой траекторией какой-то динамической системы, но может ею и не быть (очевидно, что, чтобы представлять собой фазовую траекторию динамической системы, описываемой системой ОДУ, параметрическая кривая должна быть достаточно гладкой, а также не иметь самопересечений, иначе эволюция системы не определялась бы однозначно её начальным положением). Вот пример трехмерной параметрической кривой, просматриваемой с помощью упомянутого вьюера (это — коническая спираль)

Проволочные модели для представления поверхностей
Читая на Хабре статью «Двумерные тестовые функции для оптимизации», я обнаружил в ней ссылку на статью в Википедии о тестовых функциях для оптимизации. Рассматривая красивые изображения поверхностей, приведенные в ней, я подумал, что мог бы, в качестве побочной возможности, включить в свое приложение для исследования динамических систем возможность построения и просмотра проволочных моделей для параметрических поверхностей, представленных в виде
Параметрические поверхности тоже связаны с динамическими системами — если исследовать с систему, зависящую от какого-то параметра, фазовые траектории для разных значений параметра образуют некую поверхность. Проволочная модель для параметрической поверхности может быть изображена как совокупность пространственных кривых, которые строятся в виде сетки: сначала фиксируется и строится кривая с помощью изменения , так нужно поступить для всех , изменяя их с определенным шагом. Затем, наоборот, для каждого фиксированного строится кривая при помощи изменения , и опять это делается для каждого , изменяющегося с определённым шагом. Такая поверхность имеет вид популярной в советские времена «авоськи», натянутой на прозрачную оболочку. Конечно, у такого способа представления есть определенные недостатки. Прежде всего, он не предусматривает удаления невидимых линий, которое делает поверхность по настоящему реалистичной. Нельзя также раскрасить поверхность в различные цвета или нанести на неё определенную текстуру. Тем не менее, с помощью вращения проволочной модели поверхности на экране можно представить себе, как она выглядит.
Сказано — сделано, и я быстро набросал в своей системе опцию построения проволочной модели для заданной поверхности. Для построения нужно заполнить такую форму

В форме следует указать диапазон изменения для и , количество шагов сетки для каждого из параметров и , формулы для координат точек поверхности , , и еще несколько параметров. Заданные в форме описания поверхностей можно сохранить в текстовом файле и считывать их оттуда по мере надобности. Так выглядит проволочная модель поверхности Маккормика

Еще один пример - функция Голдстайна-Прайса
Выше приведены примеры поверхностей, которые являются достаточно гладкими, не содержащими крутых пиков и глубоких впадин. Вот пример менее гладкой поверхности, задаваемой функцией Исома
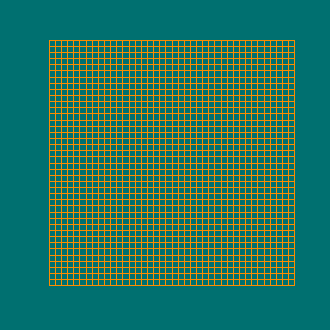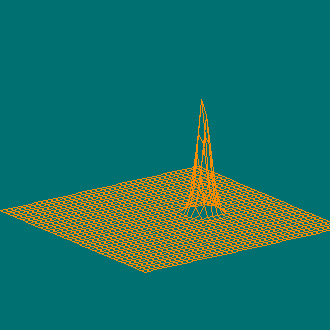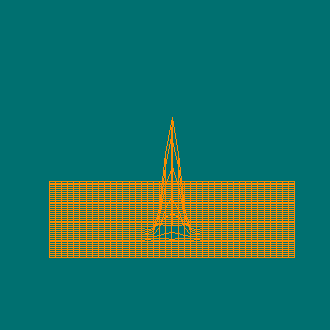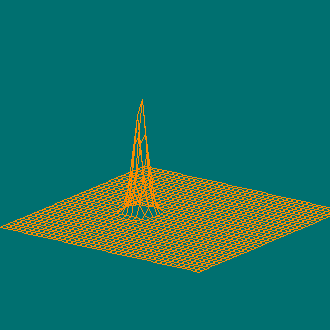
Другие примеры проволочных моделей для не слишком гладких поверхностей
Табличная функция Холдера с множеством локальных минимумов и четырьмя глобальными минимумами
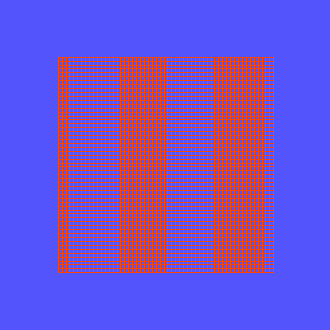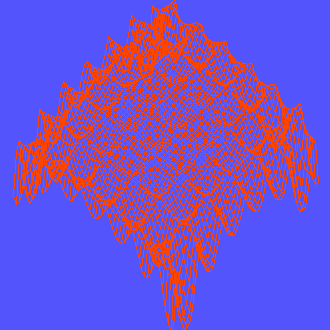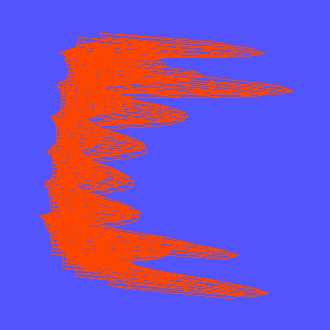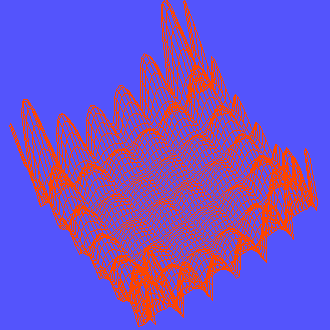
Функция Букина N 6 с множеством локальных минимумов, лежащих на гребне

Функция Розенброка, ограниченная диском. Особенность этой функции в том, что её область определения — это не прямоугольник, а круг.
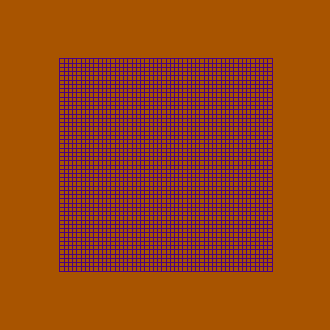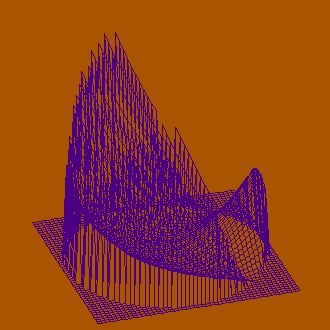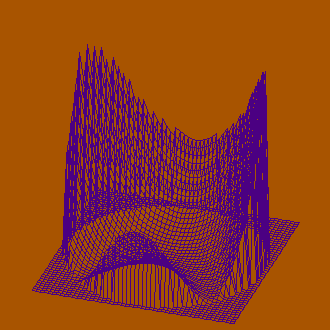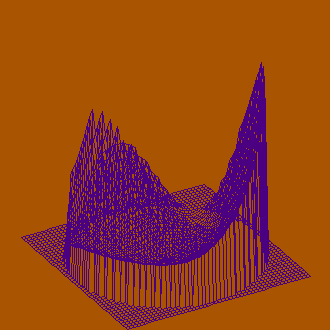
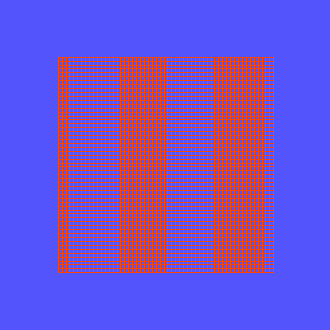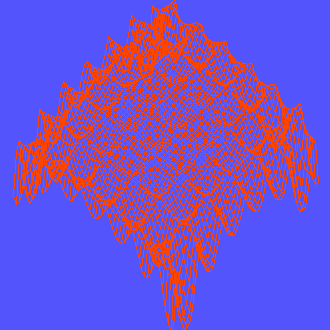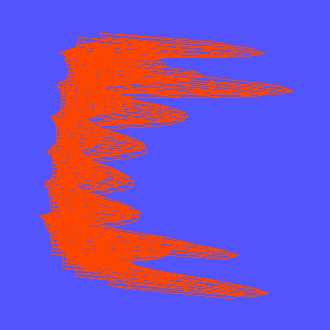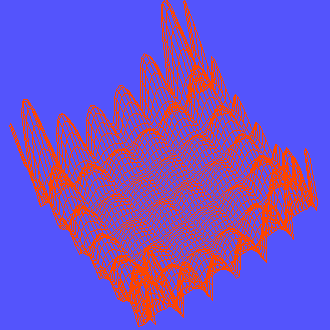
Функция Букина N 6 с множеством локальных минимумов, лежащих на гребне

Функция Розенброка, ограниченная диском. Особенность этой функции в том, что её область определения — это не прямоугольник, а круг.
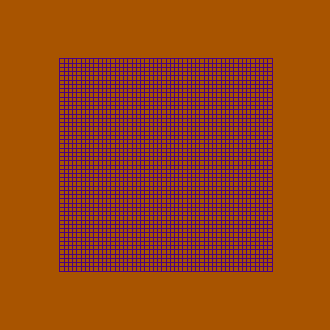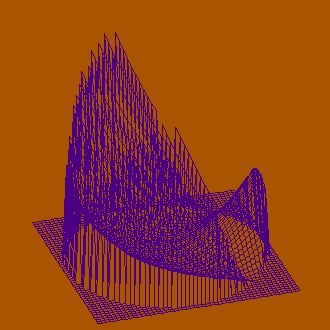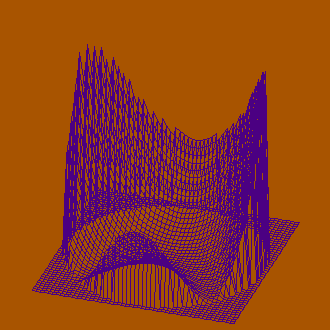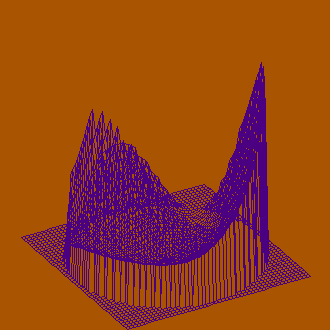
Рассмотренные примеры позволяют сделать вывод, что для анализа поверхностей проволочные модели применимы лишь ограничено, поскольку для не слишком гладких поверхностей их изображение является не очень легким для восприятия. Для приложения, с помощью которого созданы примеры это, возможно, является следствием упрощенного подхода к формированию изображения (область определения покрывается сеткой с постоянным шагом). Можно было бы применять уменьшенный шаг для областей с резкими перепадами рельефа, можно было бы также использовать сглаживание кривых, формирующих поверхность.
Тем не менее, проволочные модели трехмерных объектов (кривых и поверхностей) являются очень простыми для формирования, не требуют больших вычислительных ресурсов для своего отображения и в сочетании с возможностью быстрого просмотра с разных точек зрения могут дать достаточное представление об объектах моделирования.
Для чего предназначена проволочная конструкция, изображенная на фото в начале статьи?
Это — кротоловка. Мне показалось, что она выглядит замысловатее, чем некоторые не очень простые фазовые траектории, например, для модели Гаврилова-Шильникова («катастрофа голубого неба»).


Ссылки
- Сайт приложения для исследования динамических систем
- Virtual Library of Simulation Experiments: Test Functions and Datasets
- Wink — приложение для создания презентаций и Flash-роликов
- GifMaker — средство для создания GIF-анимаций онлайн



trir
triroakenshield.github.io/the_nurbs_book_ru/chapter4/aframe/img4_8b.html