25.06.2021 12:05
belch84 3 2800 Источник
Шланг для полива и его модель

К написанию этой публикации меня побудила следующая статья на Хабре: «Математика провисающих проводов и цепей в играх», хоть я и совершенно не занимаюсь играми.

Статья заинтересовала меня потому, что давала повод для применения моего собственного приложения для визуализации графических объектов. Первоначальное предназначение этого приложения — исследование динамических систем, которые можно представить в виде системы дифференциальных уравнений. Одним из компонентов этого приложения является вьюер (просмотрщик) трехмерных проволочных моделей. Вьюер нужен для просмотра и анализа трехмерных траекторий динамической системы, но его можно использовать и для просмотра вообще любых проволочных моделей. Недавно я добавил в свое приложение возможность генерации проволочных моделей для заданных параметрически поверхностей. Статья о цепных линиях натолкнула меня на мысль: можно ли для данной трехмерной кривой сгенерировать (и исследовать с помощью вьюера) поверхность в виде трубки, окружающей данную кривую? Такая поверхность может представлять собою модель кабеля, шланга или реального провода ненулевой толщины. Сначала это показалось мне несложной задачей, но выяснилось, что даже для такой относительно простой кривой, как цепная линия, создать трубку не так-то просто.

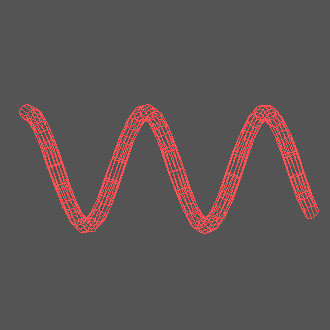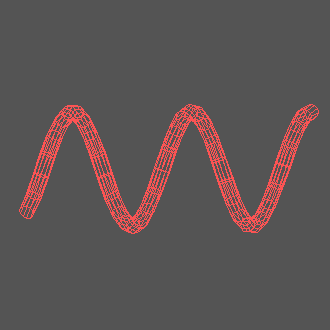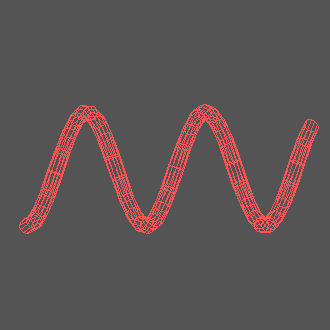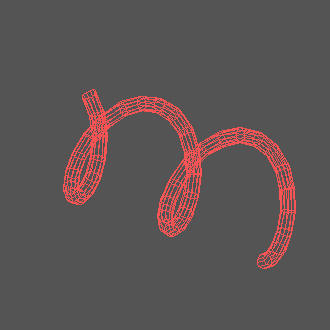
Приложение для анализа динамических систем позволяет легко строить трехмерные параметрические кривые и рассматривать их с разных сторон. Вот пример нескольких цепных линий, отличающихся значением параметра

Различные цепные линии


Хорошо бы придать этим цепным линиям объем!

Простые трубчатые поверхности


Существует очень небольшое количество кривых, для которых можно сразу выписать параметрическое уравнение поверхности-трубки. Прежде всего это цилиндр

$\begin{cases} x(u,v)=a cos(u), \ \ u \in [0,2\pi] \\y(u,v)=a sin(u), \ \ v \in [0,10] \\z(u,v)=v, \ \ \ \ \ \ \ \ \ \ \ \ \ a=0.5 \end{cases}$


Цилиндрическая поверхность


Несложно также написать уравнение поверхности-трубки для окружности, это будет тор, получаемый как поверхность вращения окружности — сечения трубки вокруг не пересекающей его оси ($R$ — расстояние от центра образующей окружности до оси вращения, $r$ — радиус образующей окружности)

$\begin{cases} x(\phi, \psi)=(R+r cos(\psi))cos(\phi) & \\ y(\phi, \psi)=(R+r cos(\psi))sin(\phi), \ \ \ \phi\in[0,2\pi], \psi\in[-\pi,\pi] & \\ z(\phi, \psi)=rsin(\psi) \end{cases}$



Тор


Для трубки вокруг винтовой линии

$\begin{cases} x(t)=R cos(t) \\ y(t)=R sin(t) \\ z(t)=h t \end{cases}$


(где $R$ — радиус, $h$ — шаг витков) уже пришлось заглянуть в Гугл, догадаться, как устроено параметрическое уравнение такой поверхности было бы нелегко ($a$ — радиус трубки)

$\begin{cases} x(t,u)=h\cdot t+\frac{R\cdot a\cdot sin(u)}{\sqrt{R^2+h^2}} \\ y(t,u)=R\cdot cos(t)-a\cdot cos(t)\cdot cos(u)+\frac{h\cdot a \cdot sin(t)\cdot sin(u)}{\sqrt{R^2+h^2}} \\ z(t,u)=R\cdot sin(t)-a\cdot sin(t)\cdot cos(u) - \frac{h\cdot a\cdot cos(t)\cdot sin(u)}{\sqrt{R^2+h^2}} \end{cases} $



Трубка для винтовой линии


Попытка написать уравнение для трубки вокруг цепной линии по аналогии с винтовой линией, закончилась для меня неудачно, ибо я запутался в получающихся при этом производных и обратных функциях.

Общая схема построения трубки


Тем не менее, применяя общий подход, описанный в книге: Alfred Gray, «Modern Differential Geometry of Curves and Surfaces with Mathematica», у меня получилось реализовать (и запрограммировать) алгоритм построения трубки для произвольной кривой. Скажу сразу, я не претендовал на создание реалистичных трубок с текстурами, тенями и прочим, пришлось ограничиться простыми проволочными моделями.

Проволочную (каркасную) модель трубчатой поверхности можно представлять себе как совокупность образующих, т.е. кривых, находящихся на одном и том же заданном расстоянии от исходной кривой, а также сечений, расположенных перпендикулярно образующим кривым. Для круглой трубки сечения — это окружности, но можно рассматривать также треугольную, квадратную трубки или трубку, имеющую в сечении любой другой правильный многоугольник (на самом деле, сечения-окружности также можно приблизить правильными многоугольниками, имеющими достаточное количество сторон). В целом модель трубки представляет собой пространственный многогранник, при достаточном количестве образующих кривых и сечений выглядящий как настоящая трубка из проволоки. Проворачивая трубку, приближая и удаляя отдельные её части с помощью вьюера проволочных моделей, можно легко проанализировать её устройство.

Построение трубок требует некоторых знаний из дифференциальной геометрии. Для генерации трубки удобно использовать базис Френе. Это подвижная тройка взаимно ортогональных единичных векторов, в каждой точке кривой состоящая из вектора касательной $\vec{T}(t)$, вектора главной нормали $\vec{N}(t)$, который перпендикулярен касательному и лежит в соприкасающейся плоскости кривой, и, наконец, вектора бинормали $\vec{B}(t)$, который определяется как векторное произведение векторов касательной и главной нормали.

Базис Френе для пространственной кривой


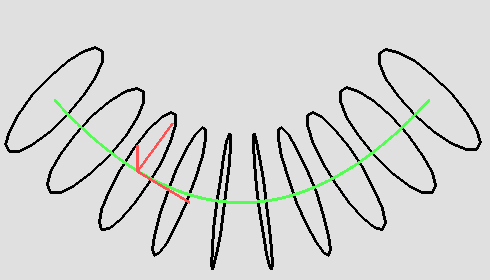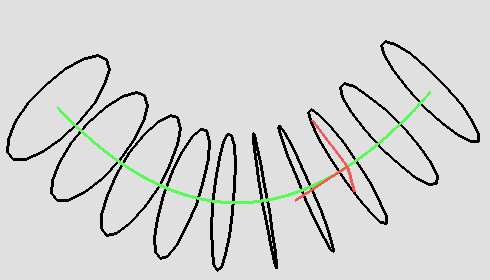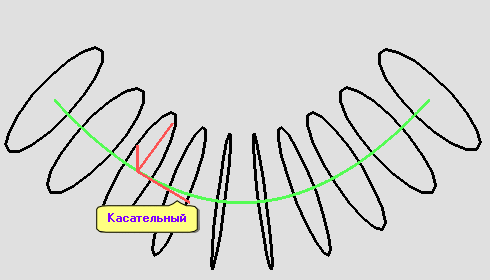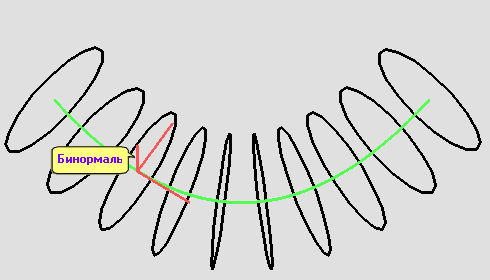
Если кривая задана параметрически, то есть в виде зависимости $r=\vec{r}(t)$, где $\vec{r}(t) $ — вектор-функция, определяющая координаты каждой точки кривой как $(x(t),y(t),z(t)), t$ — параметр, то формулы для векторов касательной и главной нормали можно выписать, определив первую и вторую производные функции $\vec{r}(t)$. Особенно просто формулы для касательной и главной нормали выглядят в случае, когда используется естественная параметризация кривой, т.е. параметром является длина кривой от начала до текущей точки $s(t)$. В этом случае

$\vec{T}(s)=\vec{r'}(s) \\ \vec{N}(s)=\frac{\vec{r''}(s)}{\|r''(s)\|} \\ \vec{B}(s)=\vec{N}(s)\times\vec{T}(s)$


где $'$ — производная функции по естественному параметру $s$, $\|\cdot\|$ — норма (длина) вектора, $\times$ — векторное произведение.

Если компоненты базиса Френе для данной кривой известны, можно сразу записать параметрическое уравнение трубчатой поверхности в векторной форме:

$Tube(s,u)=\vec{r}(s)+R\cdot (-cos(u)\cdot \vec{N}(s)+sin(u)\cdot \vec{B}(s)),$


где $\vec{r}(s)$ — исходная кривая, $\vec{N}(s)$ — главная нормаль, $\vec{B}(s)$ — бинормаль, $R$ — радиус трубки, $u \in [0,2\pi]$

(понятно, что при фиксированном $u$ это уравнение будет определять образующую кривую трубки, а при фиксированном $s$ — окружность сечения трубки, лежащую в плоскости, определяемой главной нормалью и бинормалью кривой, эта плоскость перпендикулярна исходной кривой).

Алгоритм построения трубки


В приложении для исследования динамических систем имеется возможность построения
параметрических кривых, заданных аналитически, но мне хотелось уметь строить трубки не только для них, но и для любых траекторий динамических систем, для которых не всегда (а точнее, очень редко) можно выписать аналитическую зависимость траектории от параметра. Поэтому я сформулировал для себя задачу следующим образом: построить трубку для любой дискретной кривой, состоящей из упорядоченного набора точек (фактически это будет ломанная в пространстве). Для этой ломанной, тем не менее, нужно уметь определять первую и вторую производную. Это удобно делать при помощи интерполяционных кубических сплайнов.
Сплайн — это кусочно-полиномиальная функция, которая строится на основании дискретной кривой. В узловых точках сплайн совпадает с дискретной кривой, а в промежутках представляет собой полином третьей степени. Для разных интервалов полиномы различны, но их коэффициенты подбираются так, чтобы сам сплайн, а также его первая и вторая производные были непрерывны на заданном интервале изменения параметра (то есть полиномы на соседних отрезках как бы «сшиваются»).

План построения трубки теперь выглядит так:

  • построим естественную параметризацию кривой. Для этого разобьем интервал изменения исходного параметра на равные промежутки, построим сплайны для каждой из координат исходной дискретной кривой. Для вычисления длины кривой воспользуемся равенством для длины участка параметрической кривой, лежащего между значениями параметра $t_0$ и $t_1$:

    $S(t_0,t_1)=\int_{t_0}^{t_1} \sqrt {(x'^2+y'^2+z'^2)} \text{d}t,$

    соответствующие производные найдем дифференцированием сплайнов, а интегралы определим численно, пользуясь квадратурной формулой Гаусса с пятью узлами
  • перестроим сплайны для отдельных координат с учетом естественного параметра
  • сформируем массив единичных касательных векторов, для этого нужно просто найти производные от сплайнов для отдельных координат по естественному параметру
  • сформируем массив единичных векторов главной нормали, это будут вторые производные от сплайнов для отдельных координат, кроме того, их нужно будет отнормировать, поделив на длины векторов
  • сформируем массив векторов бинормали, вычислив векторное произведение соответствующих касательных векторов и векторов главной нормали (здесь нормировка уже не нужна, результирующие векторы автоматически будут иметь единичную длину)
  • наконец, пользуясь вышеперечисленными компонентами базиса Френе, сгенерируем образующие кривые и сечения


Параметры для построения трубки


Для построения трубки в приложении для анализа динамических систем нужно задать (кроме собственно кривой, по которой строится трубка) небольшое число параметров, определяющих трубку. Параметры задаются в следующей форме:

Форма для параметров трубки


Фактически в этой форме нужно указать количество точек в образующих кривых (то же, что количество сечений), количество образующих кривых, количество точек в сечении, радиус трубки, а также цвета для образующих кривых и сечений.

Примеры трубок для параметрических кривых


Кривая Вивиани, образуется при пересечение кругового цилиндра со сферой с центром на поверхности цилиндра и радиусом, равным диаметру цилиндра

Трубка для кривой Вивиани


Линия шва на теннисном мяче — гладкая кривая на поверхности сферы, имеющая четыре точки перегиба

Трубка для линии шва на теннисном мячике


Примеры трубок для фазовых траекторий динамических систем


Переходы Джозефсона (теория сверхпроводимости) — динамическая система для описания явления протекания сверхпроводящего тока через тонкий слой диэлектрика, разделяющий два сверхпроводника

Трубка для переходов Джозефсона


Взаимодействие фотон-экситон в оптическом полупроводнике

Трубка для системы взаимодействия фотон-экситон


Другие трубки для фазовых траекторий динамических систем
Упрощенное уравнение Курамото-Цузуки для процессов, происходящих в нелинейных диссипативных средах диффузионного типа

Трубка для упрощенного уравнения Курамото-Цузуки


Одна из систем Спротта-искусственно сконструированных моделей нелинейной динамики (случай F)

Трубка для системы Спротта (F)



Поучительные ошибки, встретившиеся при отладке и исправленные

Поучительные ошибки


Когда генерация трубок только-только заработала (я использовал для отладки трубку для винтовой линии), первые варианты сгенерированной поверхности вместо аккуратного среза на краях трубки имели какой-то «клюв»

Клюв


Оказалось, что я использовал неподходящие сплайны. Для однозначного определения сплайна нужно задавать для него краевые условия. Наиболее часто встречаются условия вида $y''(x_0)=0, y''(x_N)=0$, которые соответствуют тому, что сплайн на концах интервала определения становится просто прямой. Для трубок же этот вариант неприменим, для них нужно использовать другие условия, задающие положения касательной на концах, т.е. значения производной $y'(x_0)=y_0, y'(x_N)=y_N$. Когда я воспользовался сплайнами нужного типа — «клювы» исчезли.

Другая проблема возникла с трубками для динамических систем. Я тренировался на «дверной ручке» — решении краевой задачи для системы

$\begin{cases} y_1' = y_2 \\ y_2' = 1.5 y_1^2, \ \ \ \ y_1(0)=4, \ \ y_1(1)=1 \end{cases}$


Здесь трубка содержала близко к концам участки с «осиной талией»

Дверная ручка с осиной талией


В этом случае выяснилось, что кривая, являющаяся решением системы, имеет на соответствующих интервалах точки перегиба, в которых вторая производная, т.е. главная нормаль меняет свой знак (оставаясь при этом главной нормалью). Пришлось такие точки отслеживать и разворачивать в них главную нормаль. После этого «дверные ручки» стали нормальными, пригодными для установки на любую дверь.


Заключение


Я не уверен, что описанная схема содержит что-либо новое в визуализации трубок, и не знаю, какие методы для их построения используются в настоящих «взрослых» графических системах — возможно, подобные, а возможно — в корне отличающиеся. Тем не менее, мне было интересно разобраться в проблеме и создать работающую систему для построения трубок, шлангов, кабелей и проводов.

А получилось ли сформировать трубки для цепных линий, упомянутых в начале публикации?
Конечно, для цепных линий трубки генерировать очень легко и приятно

Трубки для различных цепных линий


Ссылки



Фотография шланга для полива в начале статьи сделана в «Concordia Celes Hotel», Окурджалар, Аланья, Турция, в июне 2021 года.