Древняя история

Давным-давно, очень много лет назад в букинистическом магазине я купил книгу П.Грогоно «Программирование на языке Паскаль». У меня математическое образование, а для обучения программированию (которое не было основным предметом) у нас использовался язык ALGOL-68, поэтому Паскаль, будучи алголоподобным языком, был для меня относительно простым и понятным. Практически использовать эту книжку мне довелось на одном из первых мест работы, когда понадобилось создать систему аппроксимации одномерных кривых по Методу Наименьших Квадратов (МНК). Среди прочих нужна была возможность представления аппроксимирующих кривых в виде линейной комбинации произвольных базисных функций. Одним из примеров в книге Грогоно была программа, реализующая простой калькулятор, на вход которого подавалась строка, содержавшая выражение из чисел, знаков операций и скобок, а на выходе было числовое значение этого выражения:

На основе этой программы я написал интерпретатор выражений (формул), который позволял использовать в выражении простые переменные, типа X или Y, а также элементарные функции вроде SIN(X). Задав значения переменных и имея синтаксически правильную формулу в виде строки, можно было вычислить числовое значение этой формулы. Сама система позволяла задать набор базисных функций типа или , построить по нему МНК-аппроксимацию, а затем вывести результаты (точки исходной кривой и аппроксимацию) в виде графиков. Все это было написано на Паскале для компьютеров ДВК.

Следующим событием была покупка книги   «Решение обыкновенных дифференциальных уравнений: нежесткие задачи», авторы: Хайрер Э., Нёрсетт С., Ваннер Г., посвященной численным методам решения систем Обыкновенных Дифференциальных Уравнений (ОДУ). Среди прочего в книге приводились программы на языке FORTRAN, реализующие различные методы интегрирования систем ОДУ. Итак, к тому моменту у меня был работающий интерпретатор формул, готовые отлаженные программы для интегрирования ОДУ и некоторые навыки программирования графики. После беглого прочтения книги мне пришла в голову мысль: а нельзя ли все это объединить и написать программу, которая позволит быстро задать уравнения системы и начальные условия, а потом получить наглядное решение в виде графиков? Такие системы тогда уже существовали (мне был известен PHASER), но было интересно попробовать, как это получится у меня. Интерпретатор формул для решения такой задачи не годился, поскольку при численном интегрировании системы ОДУ требуется очень много вычислений правой части, а интерпретатор для каждого вычисления должен проделать небыстрый синтаксический разбор («парсинг») выражения. Пришлось превратить интерпретатор в компилятор формул, он преобразовывал формулу во внутреннее представление, которое затем могло использоваться множество раз при вычислениях. Для построения графиков, а также любых зависимостей от решения (вроде фазовой траектории) использовались интерполирующие сплайны. Все это писалось уже на Турбо Паскале для PC AT 286 (программу для интегрирования систем ОДУ из книги Хайрера и других я перевел на Паскаль  с FORTRANA’a) и не сразу, но заработало.

Изменения, дополнения, усовершенствования

Занимаясь на своей основной работе совсем другими задачами, я время от времени возвращался к этой программе, и она дожила до нынешних дней, превратившись в Windows-приложение для исследования динамических систем с непрерывным временем, которые можно описать системой ОДУ. Когда-то я назвал его DEREK, в этом имени мне чудилось нечто от как бы производной (derivative) и от уравнения (equation). Среди прочего пришлось усовершенствовать компилятор формул, добавив к нему возможность аналитического дифференцирования выражений (для вычисления якобиана системы, он используется при численном интегрировании жестких систем, а также для вычисления показателей Ляпунова). Еще удалось добавить возможность просмотра трехмерных фазовых траекторий при помощи их вращения, приближения и удаления. Понадобилось также включить реализацию отдельного численного метода для решения жестких систем ОДУ (взята из книги Хайрера и соавторов о жестких системах).

Особое внимание я старался уделять обработке ошибок, чтобы при различных случаях переполнения и деления на 0, которые вполне могут встретиться при попытках решения совершенно произвольных систем, программа не прекращала выполнения и не выдавала непонятных сообщений (вроде «Runtime error 203 at address 04BF»), чтобы сообщения были краткими, но понятными, и чтобы после ошибки можно было бы продолжать работу с программой.

Динамические системы повсюду

С помощью динамических систем можно построить модели самых разнообразных явлений, происходящих в природе и в человеческом обществе. Если для какого-либо процесса можно указать зависимость между скоростью изменения характеризующих его величин и самими этими величинами - значит, можно записать систему обыкновенных дифференциальных уравнений, решение (интегрирование) которой позволит понять и предсказать развитие этого процесса.

где независимая переменная, - зависимые переменные, - параметры (константы) системы, - производная от

Лишь для очень небольшой доли реально существующих динамических систем можно решить описывающие их дифференциальные уравнения аналитически, то есть в виде явных формул. В большинстве же случаев приходится прибегать к численным методам решения. DEREK предназначен как раз для того, чтобы сделать это процесс простым и увлекательным.

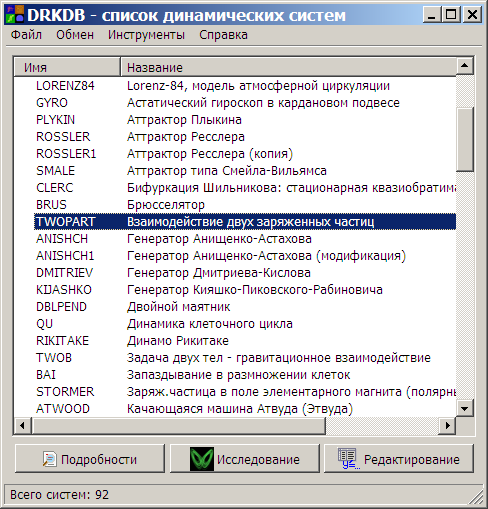
Одновременно с усовершенствованием программы я собирал, так сказать, коллекцию интересных динамических систем. К настоящему моменту DEREK содержит большое количество (думаю, что большее, чем какая бы то ни было аналогичная программа) примеров реальных динамических систем из механики, физики, химии, биологии и прочих областей человеческого знания (есть и модель для эпидемии COVID-19). Многие примеры снабжены ссылками на ресурсы в Интернет, которые включают в себя подробные описания систем, историю их исследования и прочее.
Большинство из систем, включенных в базу данных DEREK'а, являются нелинейными, значительное их количество демонстрирует хаотическое поведение, многие при определенных условиях обладают странными аттракторами. Аттрактор - это притягивающее множество динамической системы, к которому система приближается с течением времени. Аттракторы могут быть простыми (например, если система постепенно приходит в состояние покоя, её аттрактор - это просто точка пространства всех возможных состояний системы), а могут быть устроены весьма сложно и странно. Изображения некоторых аттракторов могут по-настоящему завораживать.

Современное состояние

Что же система умеет сейчас? DEREK позволяет:

• задать описание системы в виде совокупности дифференциальных уравнений (не более 25-ти), начальных условий, а также параметров, входящих в уравнения (не более 30-ти)

• найти ошибки в описании системы, точно указав место и суть ошибки

• автоматически выбрать параметры численного метода для решения системы. Количество параметров для управления численным решением системы невелико, а их смысл весьма прозрачен, так что запутаться в них сложно

• построить наглядные графики решений и любых зависящих от решения величин.  DEREK может сам масштабировать поле для графиков для наилучшего их  отображения, но допускает и задание поля вручную

• исследовать трехмерное изображение фазовой траектории. DEREK умеет вращать трехмерную фазовую траекторию, а также приближать и удалять её.

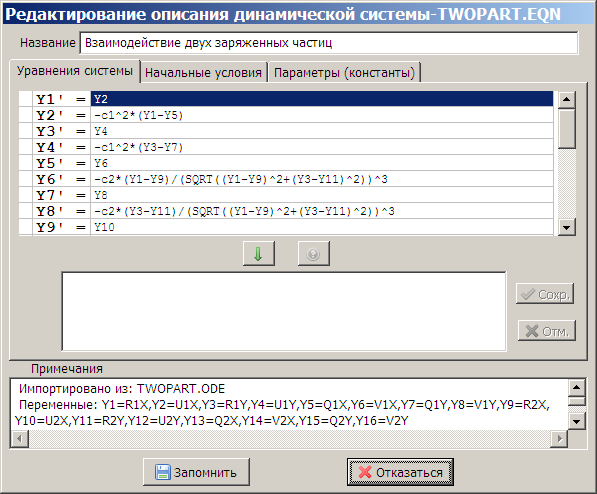
 DEREK также включает в себя некоторые специальные методы для анализа динамических систем:

• построение «семейства» решений, зависящих от одного или двух параметров или от набора различных начальных условий. Для каждого значения параметра строится график, по которому можно следить за изменением поведения системы. С помощью внешних программных средств (вроде WINK или GIFMAKER) это можно использовать для создания анимированных изображений эволюции динамических систем

• построение «сечений Пуанкаре» - множества точек пересечения траектории  системы с заданной плоскостью. Сечения Пуанкаре позволяют лучше понять  характер движения 

• вычисление «показателей Ляпунова» - наборов чисел, характеризующих  поведение динамической системы при бесконечной эволюции и  не зависящих от начальных  условий. DEREK умеет также строить график зависимости показателей Ляпунова от параметра системы. Для нелинейных систем не менее чем третьего порядка наличие положительного показателя Ляпунова при условии отрицательности суммы всех показателей означает, что система ведёт себя хаотически

Есть у DEREK’а и в каком-то смысле побочные возможности, которые, тем не менее, полезны при работе с динамическими системами:

• построение графиков кривых, заданных параметрически, двумерных и трехмерных

• построение  графиков двумерных точечных кривых, заданных набором точек

• реконструкция систем ОДУ - построение системы дифференциальных уравнений, решением которой является одна или нескольких заданных зависимостей каких-либо величин от времени («временной ряд»)

• решение краевых задач (только для систем второго порядка)

  Необычная черта DEREK'а - его способность обращаться с набором известных ему динамических систем как с базой данных - позволяет осуществлять поиск систем по заданной совокупности сложных критериев. При этом можно получать ответы на запросы, подобные следующим: «выбрать системы не менее чем третьего порядка и притом неавтономные» или «выбрать системы, которые модифицировались после 1 марта 2015 г., правые части которых - полиномы не более чем второго порядка от переменных системы» или даже: «выбрать системы, описываемые уравнением Штурма-Лиувилля».

Кому это может быть нужно?

Систем такого типа существует немало (PHASER, Dynamics Solver Хуана Агиррегабириа, XPP Барда Эрментраута). По сравнению с ними DEREK по-настоящему прост и нагляден. Если представить себе исследователей, которые не являются физиками, математиками или программистами, но которым нужно решать системы ОДУ (например, сейчас это могут быть химики или биологи), не особенно вдаваясь в подробности численных методов - DEREK может пригодиться. MATLAB решит подобную задачу хорошо и качественно, возможностей у него намного больше, но с помощью DEREK'а результат будет получен быстрее и будет более наглядным. Скорее всего, это не инструмент для ученых, но вот для студентов и даже школьников его использование может иметь смысл. Теория хаоса, странные аттракторы, теория колебаний, применение динамических систем в биологии, химии или метеорологии - DEREK подойдет для практических занятий по таким учебным курсам.

DEREK - некоммерческий проект, большинство его функций работает в демонстрационной версии. 

  Его недостатки - прежде всего достаточно архаичная и достаточно медленная графика, особенно это заметно при просмотре трехмерных фазовых траекторий. Также - жестко зафиксированные имена переменных: независимая переменная - это всегда X, зависимые переменные - всегда Y1, Y2 … Y25, константы (параметры) системы - всегда C1, C2 … и т.д.

Последняя версия DEREK’а написана на Free Pascal и Lazarus. Для построения обычных и анимированных изображений динамических систем помимо DEREK'а я использую также XnView, Wink, GifMaker.

Примеры

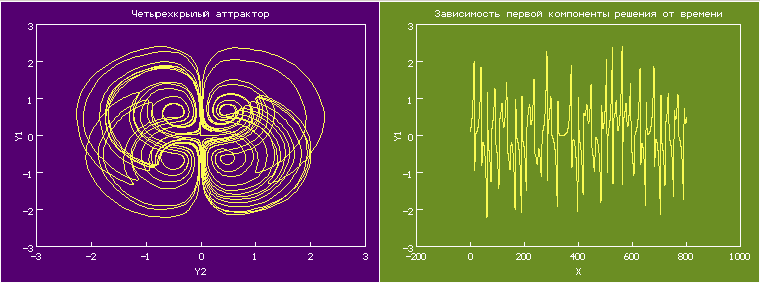
Четырехкрылый аттрактор исследуется в статье: Zenghui Wang, Yanxia Sun, Barend Jacobus van Wyk, Guoyuan Qi, Michael Antonie van Wyk, A 3-D four-wing attractor and its analysis

При данном значении параметра система демонстрирует квазипериодическое поведение (на это указывают точки сечения Пуанкаре, располагающиеся на двух замкнутых кривых)

Это значение параметра системы соответствует хаотическому поведению (точки сечения Пуанкаре заполняют некоторую область на плоскости)

Другие анимированные изображения

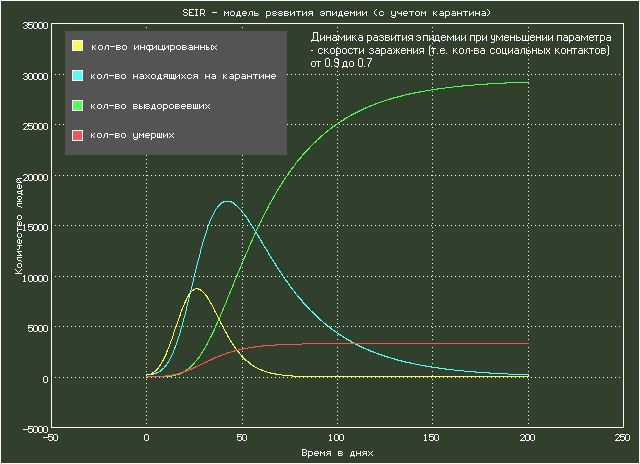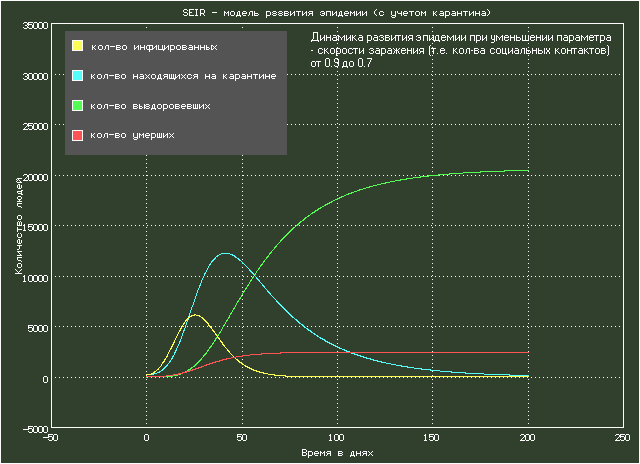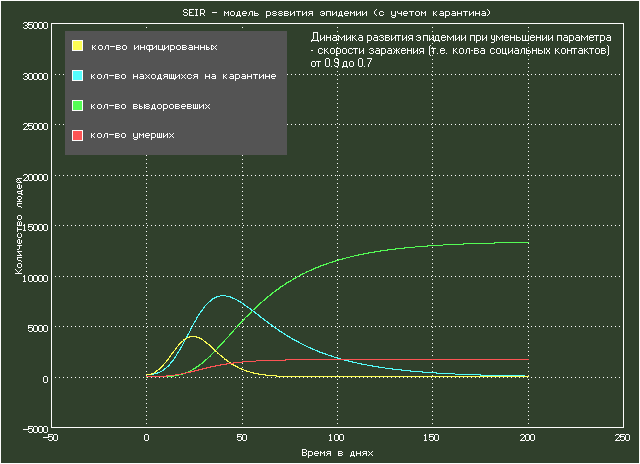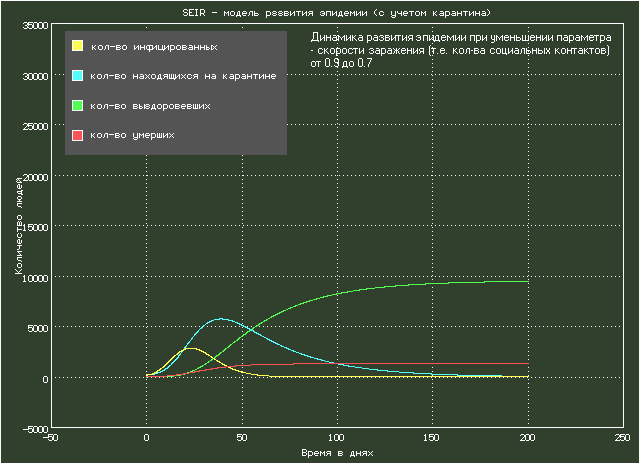
Описание модели взято из статьи: Etienne Cheynet, Generalized SEIR Epidemic Model (fitting and computation). В статье анализируется эпидемия коронавируса COVID-19 в различных регионах планеты. На рисунке показана анимация с параметрами, примерно соответствующими Италии. Модель представляет собой систему из шести дифференциальных уравнений.

Модель атмосферной циркуляции для тропического циклона, описана в статье:
Safieddine Bouali, Jos Leys Tropical Cyclone Genesis: A Dynamician's Point of View

Траектория подвергнута вращению, чтобы ?можно было её рассмотреть получше

На анимации представлены траектории двух динамических систем, положения равновесия которых образуют пространственные кривые, лежащие в одной плоскости (парабола в одном случае и окружность в другом). Системы описаны в статьях:
Jiri Petrzela and Tomas Gotthans, New Chaotic Dynamical System with a Conic-Shaped Equilibrium Located on the Plane Structure
Jiri Petrzela, Tomas Gotthans, Milan Guzan, Current-Mode Network Structures Dedicated for Simulation of Dynamical Systems with Plane Continuum of Equilibrium

Участие в конкурсах Wikimedia

Изображения, созданные с помощью DEREK'а, принимали участие ( и не просто принимали участие, а иногда и побеждали) в конкурсах научной фотографии, проводимых фондом Wikimedia в Украине (в разделе «Нефотографические изображения»). Вот изображение, победившее в 2015 году.

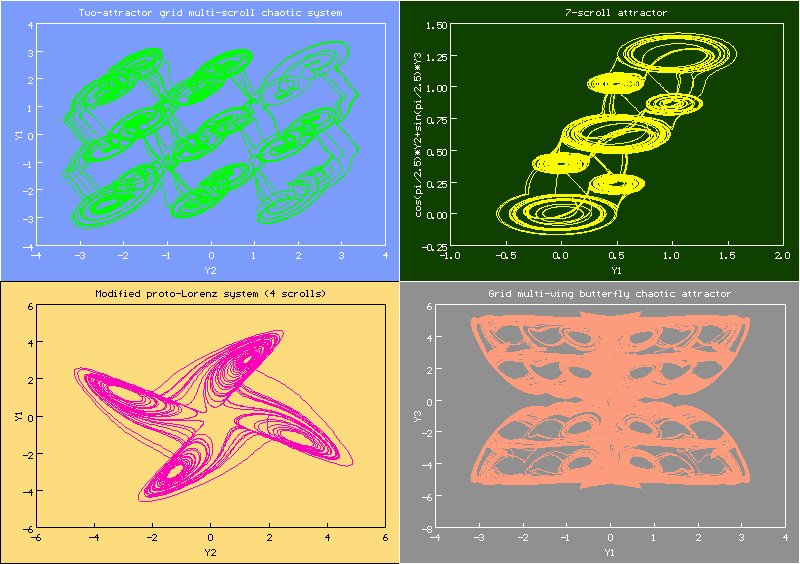
https://commons.wikimedia.org/wiki/File:Multiscroll_attractors_of_dynamical_systems.png

Другие изображения, созданные с помощью DEREK'а, принимавшие участие в конкурсах Wikimedia

Ссылки

• Курс лекций С.П.Кузнецова «Динамический хаос»

• PHASER - универсальный симулятор для изучения динамических систем

• Dynamics Solver - мощный инструмент изучения нелинейных динамических систем (автор-Хуан Агиррегабириа)

• XPP - средство для исследования динамических систем (автор-Бард Эрментраут)

• XnView - программа для просмотра и обработки изображений

• Wink - приложение для создания презентаций и Flash-роликов

• GifMaker - средство для создания GIF-анимаций онлайн

• Сайт приложения DEREK