Однажды, выполнив в Гугле запрос "Three body problem" ("Задача трёх тел"), я был просто поражен - первая страница результатов состояла только из ссылок на роман китайского писателя-фантаста Лю Цысиня с соответствующим названием, а также на телесериал, снятый по этому роману, т.е. ссылок на собственно задачу трёх тел не было вообще! Мне это показалось удивительным и несправедливым, поскольку сама по себе задача трёх тел тоже может выглядеть увлекательной в популярном изложении. В этой публикации я постарался привести некоторые доказательства этого утверждения.
Постановка задачи и её разновидности
Итак, задача трёх тел состоит в определении траекторий движения трех массивных тел, которые притягиваются в соответствии с Законом всемирного тяготения с силой, прямо пропорциональной массам тел и обратно пропорциональной квадрату расстояния между ними (эта сила центральная, т.е. действует в направлении центров массы тел). Для решения конкретной задачи начальные положения и скорости трех тел должны быть предварительно заданы. На самом деле аналогичные задачи могут возникать и для других видов взаимодействия, например, для заряженных частиц, притягивающихся или отталкивающихся по закону Кулона, но при гравитационном взаимодействии существует только притяжение (хотя я здесь иногда с благоговейным изумлением читаю статьи про устройство Вселенной и темную материю, поэтому готов поверить, что, возможно, и отталкивание тоже может происходить). В любом случае, наблюдение за гравитационным взаимодействием проще, чем исследование заряженных частиц.
В трехмерном пространстве движение трёх тел описывается тремя координатами и тремя скоростями на каждое тело, запись уравнений движения для Закона всемирного тяготения приводит к системе 18-ти дифференциальных уравнений, связывающих координаты, скорости и ускорения тел. Этот случай образует полную задачу трёх тел. Существуют также важные частные случаи. В начальный момент три тела определяют плоскость в трехмерном пространстве, если начальные скорости таковы, что не содержат составляющих, направленных перпендикулярно этой плоскости, то и далее тела будут перемещаться в пределах первоначальной плоскости. Этот случай называется плоской задачей трех тел (Planar 3 Body Problem, P3BP), для его описания достаточно 12-ти дифференциальных уравнений. Наконец, если масса одного из тел намного меньше масс двух других, а движение происходит в одной плоскости, говорят о плоской ограниченной задаче трех тел (Planar Restricted 3 Body Problem, PR3BP), она описывается всего четырьмя дифференциальными уравнениями для двух координат и двух компонент скорости меньшего тела. Существует еще один частный, но очень важный вариант ограниченной задачи - круговая ограниченная задача (Circular Restricted 3 Body Problem, CR3BP), в которой рассматривается система, где наименьшее тело с пренебрежимо малой массой испытывает гравитационное воздействие двух других тел, меньшее из которых вращается вокруг большего по круговой орбите, при этом траектория наименьшего тела (космического корабля) НЕ ЛЕЖИТ в той же плоскости, в которой происходит вращение меньшего тела вокруг большего. В этом случае для описания движения космического корабля потребуется 6 дифференциальных уравнений - по одному для каждой из трех координат тела и по одному для для каждой из трех компонент скорости тела.
Общая система уравнений для задачи трех тел в векторной форме выглядит так:
где - радиус-вектора трёх точек (центров массы тел),
- массы трёх тел,
- гравитационная постоянная.
Избавимся сразу от лишних деталей. Будем считать массой произведение истинной массы на гравитационную постоянную, также, поскольку решение уравнений зависит не собственно от масс, а от их отношений, разделим все массы на наибольшую (или наименьшую), в результате массы будут относительно небольшими числами. Я приведу здесь уравнения для разных видов задачи трёх тел в текстовом виде. Далее в некоторых случаях будут указываться начальные условия, это позволит каждому скопировать и внести уравнения и начальные условия в свою любимую программу для решения дифференциальных уравнений и воспроизвести картинки из этой публикации.
Полная задача трёх тел
(X1,Y1,Z1), (X2,Y2,Z2), (X3,Y3,Z3) - трехмерные координаты трёх тел
m1,m2,m3 - массы тел
X1' = VX1
Y1' = VY1
Z1' = VZ1
X2' = VX2
Y2' = VY2
Z2' = VZ2
X3' = VX3
Y3' = VY3
Z3' = VZ3
VX1' = -m2*(X1-X2)/((X1-X2)^2+(Y1-Y2)^2+(Z1-Z2)^2)^1.5-m3*(X1-X3)/((X1-X3)^2+(Y1-Y3)^2+(Z1-Z3)^2)^1.5
VY1' = -m2*(Y1-Y2)/((X1-X2)^2+(Y1-Y2)^2+(Z1-Z2)^2)^1.5-m3*(Y1-Y3)/((X1-X3)^2+(Y1-Y3)^2+(Z1-Z3)^2)^1.5
VZ1' = -m2*(Z1-Z2)/((X1-X2)^2+(Y1-Y2)^2+(Z1-Z2)^2)^1.5-m3*(Z1-Z3)/((X1-X3)^2+(Y1-Y3)^2+(Z1-Z3)^2)^1.5
VX2' = -m3*(X2-X3)/((X2-X3)^2+(Y2-Y3)^2+(Z2-Z3)^2)^1.5-m1*(X2-X1)/((X1-X2)^2+(Y1-Y2)^2+(Z1-Z2)^2)^1.5
VY2' = -m3*(Y2-Y3)/((X2-X3)^2+(Y2-Y3)^2+(Z2-Z3)^2)^1.5-m1*(Y2-Y1)/((X1-X2)^2+(Y1-Y2)^2+(Z1-Z2)^2)^1.5
VZ2' = -m3*(Z2-Z3)/((X2-X3)^2+(Y2-Y3)^2+(Z2-Z3)^2)^1.5-m1*(Z2-Z1)/((X1-X2)^2+(Y1-Y2)^2+(Z1-Z2)^2)^1.5
VX3' = -m1*(X3-X1)/((X1-X3)^2+(Y1-Y3)^2+(Z1-Z3)^2)^1.5-m2*(X3-X2)/((X3-X2)^2+(Y3-Y2)^2+(Z3-Z2)^2)^1.5
VY3' = -m1*(Y3-Y1)/((X1-X3)^2+(Y1-Y3)^2+(Z1-Z3)^2)^1.5-m2*(Y3-Y2)/((X3-X2)^2+(Y3-Y2)^2+(Z3-Z2)^2)^1.5
VZ3' = -m1*(Z3-Z1)/((X1-X3)^2+(Y1-Y3)^2+(Z1-Z3)^2)^1.5-m2*(Z3-Z2)/((X3-X2)^2+(Y3-Y2)^2+(Z3-Z2)^2)^1.5
Плоская задача трёх тел
(X1,Y1), (X2,Y2), (X3,Y3) - плоские координаты трёх тел
m1,m2,m3 - массы тел
X1' = VX1
X2' = VX2
X3' = VX3
Y1' = VY1
Y2' = VY2
Y3' = VY3
VX1' = m2*(X2-X1)/((X1-X2)^2+(Y1-Y2)^2)^1.5+m3*(X3-X1)/((X1-X3)^2+(Y1-Y3)^2)^1.5
VX2' = m3*(X3-X2)/((X2-X3)^2+(Y2-Y3)^2)^1.5+m1*(X1-X2)/((X2-X1)^2+(Y2-Y1)^2)^1.5
VX3' = m1*(X1-X3)/((X3-X1)^2+(Y3-Y1)^2)^1.5+m2*(X2-X3)/((X3-X2)^2+(Y3-Y2)^2)^1.5
VY1' = m2*(Y2-Y1)/((X1-X2)^2+(Y1-Y2)^2)^1.5+m3*(Y3-Y1)/((X1-X3)^2+(Y1-Y3)^2)^1.5
VY2' = m3*(Y3-Y2)/((X2-X3)^2+(Y2-Y3)^2)^1.5+m1*(Y1-Y2)/((X2-X1)^2+(Y2-Y1)^2)^1.5
VY3' = m1*(Y1-Y3)/((X3-X1)^2+(Y3-Y1)^2)^1.5+m3*(Y2-Y3)/((X3-X2)^2+(Y3-Y2)^2)^1.5
Ограниченная задача трёх тел
(X,Y) - координаты тела с пренебрежимо малой массой (космического корабля)
m1,m2 - массы тел
X' = VX
Y' = VY
VX' = X+2*Y4-m1*(X+m2)/((X+m2)^2+Y^2)^1.5-m2*(X-m1)/((X-m1)^2+Y^2)^1.5
VY' = Y-2*Y3-m1*Y/((X+m2)^2+Y^2)^1.5-m2*Y/((X-m1)^2+Y^2)^1.5
Круговая ограниченная задача трёх тел
(X,Y,Z) - координаты тела с пренебрежимо малой массой (космического корабля)
mu - отношение массы меньшего тела (которое вращается вокруг большего) к сумме масс меньшего и большего
X' = VX
Y' = VY
z' = VZ
VX' = 2*VY+X-(1-mu) * (X+mu)/((X+mu)^2+Y^2+Z^2)^1.5-mu * (X-1+mu)/((X-1+mu)^2+Y^2+Z^2)^1.5
VY' = -2*VX+Y-(1-mu) * Y/((X+mu)^2+Y^2+Z^2)^1.5-mu * Y/((X-1+mu)^2+Y^2+Z^2)^1.5
VZ' = -(1-mu) * Z/((X+mu)^2+Y^2+Z^2)^1.5-mu * Z/((X-1+mu)^2+Y^2+Z^2)^1.5
Первые попытки решения задачи трех тел, случаи Эйлера и Лагранжа
Исторически первыми решениями задачи трех тел были решения Эйлера и Лагранжа, найденные соответственно в 1767 и 1772 годах. В обоих случаях для решения использовались специально подобранные начальные условия. В случае Лагранжа тела изначально располагаются в вершинах равностороннего треугольника, скорости тоже необходимо подобрать согласованными. Специальная замена переменных позволяет свести задачу трех тел к трем задачам двух тел (то есть тела взаимодействуют попарно), причем решения двух из этих задач можно выразить через решение третьей задачи). Траекториями движения являются эллипсы, для случая равных масс они одинаковы и повернуты друг относительно друга на 120 градусов, в общем случае эллипсы имеют разные размеры и расположение. Во время движения тела постоянно образуют равносторонний треугольник, размеры и положение которого постоянно меняются. Не берусь выписать решения в аналитическом виде, но их можно найти численно

Анимированное движение тел для соотношения масс 1:2:3

В случае Эйлера тела изначально располагаются на одной прямой (тоже не где попало, координаты и скорости должны быть согласованы), траекториями движения тоже служат эллипсы, а расположение на одной прямой во время движения сохраняется, но сама прямая изменяет своё положение.
Решения Эйлера и Лагранжа до сих пор остаются единственными известными точными решениями задачи трех тел. Они имеют не очень большое практическое значение, поскольку требуют очень точного задания начальных условий, которое трудно реализовать физически (точнее будет сказать, что решения неустойчивы, устойчивость они приобретают только в случае, когда масса одного из тел значительно меньше масс двух других).
Плоская задача трех тел, периодические траектории
В конце XIX века Анри Пуанкаре доказал существование бесконечного числа периодических решений ограниченной (плоской) задачи трех тел, а также указал методы продолжения этих решений на общую задачу трёх тел. С появлением и совершенствованием компьютеров исследователи стали обнаруживать все возрастающее количество плоских периодических траекторий для задачи трех тел, некоторые из этих траекторий выглядят довольно красиво. В этом разделе рассматриваются только случаи тел равной массы (она принимается равной 1).
Семейство Брука-Эно-Хаджидиметриу (1975)

Анимированное изображение движения тел, орбита Брука, случай R 4
Здесь изображено два периода

Начальные условия для орбиты Брука, случай R 4
T0 = 0, T1 = 5.4
X1(T0) = 0.8733047091
X2(T0) = -0.6254030288
X3(T0) = -0.2479016803
Y1(T0) = 0
Y2(T0) = 0
Y3(T0) = 0
VX1(T0) = 0
VX2(T0) = 0
VX3(T0) = 0
VY1(T0) = 1.010776444
VY2(T0) = -1.683353346
VY3(T0) = 0.6725769022
Семейство Шувакова-Дмитрашиновича (2013)

Анимированное изображение движения тел, орбита Шувакова-Дмитрашиновича (Dragonfly)

Начальные условия для орбиты Шувакова-Дмитрашиновича (Dragonfly)
T0 = 0, T1 = 22
X1(T0) = -1
X2(T0) = 1
X3(T0) = 0
Y1(T0) = 0
Y2(T0) = 0
Y3(T0) = 0
VX1(T0) = 0.08058
VX2(T0) = 0.08058
VX3(T0) = -0.16116
VY1(T0) = 0.58884
VY2(T0) = 0.58884
VY3(T0) = -1.17768
Орбиты Шувакова-Дмитрашиновича имеют довольно поэтические названия - Butterfly (Бабочка), Moth (Мотылёк), Dragonfly (Стрекоза), Goggles (Защитные очки), Yin-Yang (Инь-Ян), есть еще Bumblebee (Шмель) и Yarn (Пряжа)
Семейство Шина (Sheen 2016)

Анимированное изображение движения тел, орбита Шина (Овал, кошачья мордочка, космический корабль)
Здесь изображено два периода

Начальные условия для орбиты Шина (Овал, кошачья мордочка, космический корабль)
T0 = 0, T1 = 5.1
X1(T0) = 0.5363870734
X2(T0) = -0.2520991265
X3(T0) = -0.2757066017
Y1(T0) = 0.05408860501
Y2(T0) = 0.6945273277
Y3(T0) = -0.3359335893
VX1(T0) = -0.5693795856
VX2(T0) = 0.07964461525
VX3(T0) = 0.4897349703
VY1(T0) = 1.255291103
VY2(T0) = -0.4586259973
VY3(T0) = -0.7966651052
Начальные условия для орбит из этого раздела взяты из Галереи орбит для плоской задачи трёх тел. Это прекрасный сайт, но анимации движения на нем даны в представлении на сфере, это полезно для понимания топологической структуры орбит, но иногда делает движение совершенно непонятным
Ограниченная задача трех тел, полеты к Луне
Ограниченная задача трех тел имеет более явное практическое значение, поскольку с её помощью можно описать движение космического корабля в космическом пространстве, в поле гравитационного воздействия небесных тел (в таких системах как Земля-Луна или Солнце-Земля). Первые попытки достижения космических тел с Земли вызвали необходимость решения задачи о траекториях, по которым должен перемещаться космический корабль, чтобы достигнуть Луны. Затруднительно перечислить имена всех исследователей, внесших свой вклад в построение орбит для реальных полетов к другим небесным телам, но среди первых следует упомянуть американца Ричарда Аренсторфа и советского ученого Всеволода Егорова. Основополагающая работа Егорова "О некоторых задачах динамики полета к Луне", вышедшая в 1957, содержала теоретическое решение вопроса о минимальных скоростях, необходимых для полета к Луне, решение задач о попадании в Луну и облёте Луны, также была рассмотрена задача о разгоне ракеты с помощью лунной гравитации (теперь это называется гравитационным маневром).
Среди прочего Егоров указал траектории, которые можно использовать для исследования Луны без постоянно работающего двигателя ракеты, только за счет гравитационного взаимодействии с Землей и Луной. Не вдаваясь в тонкости классификации траекторий полета к Луне, можно выделить два основных класса траекторий - периодические и непериодические. Периодические траектории, в свою очередь, бывают долётными и облётными. Долётные траектории позволяют приблизится к Луне на относительно небольшое расстояние, взглянуть на неё, так сказать, одним глазком и вернуться в сферу действия притяжения Земли. Облётные траектории позволяют, облетев Луну, увидеть её обратную сторону, которая, как известно, с Земли не видна.
По-английски долётные траектории называются cislunar, а облётные - circumlunar. В этом разделе будут рассматриваться только траектории, лежащие в одной плоскости (coplanar по-английски), т.е. те, которые можно обозначить как coplanar cislunar и coplanar circumlunar.
Эта цитата из книги: Виктор Себехей, "Теория орбит" объясняет, почему важно исследовать периодические орбиты:
Пуанкаре в первом томе своих Мethodes Nouvelles рассматривает периодические орбиты как единственный путь в исследовании задачи трех тел и подчеркивает их важную роль. Если дано частное решение ограниченной задачи, то всегда можно найти периодическое решение (с периодом, который может быть очень большим) такое, что разница между двумя этими решениями будет сколь угодно малой для любого заданного отрезка времени. Весьма интересна интерпретация Шварцшильда по поводу высказывания Пуанкаре, данная им на языке фазового пространства. В произвольно близкой окрестности любой точки в фазовом пространстве имеется точка, представляющая периодическую орбиту. Иначе говоря, небольшие изменения любых начальных условий приводят к периодической орбите, в общем случае с весьма большим периодом. Как в своей первоначальной форме, так и в модифицированной предложение Пуанкаре сводится к использованию периодических орбит в качестве исходных орбит.
Пользуясь только численным решением системы дифференциальных уравнений для ограниченной задачи трех тел, а также некоторыми рецептами, указанными в работах Егорова и других исследователей, можно самостоятельно построить некоторые периодические траектории, подходящие для исследования Луны. Эти рецепты таковы - нужно начинать с наиболее близкой к Луне точки траектории (она же наиболее удаленная от Земли), задавая её координаты, а также скорость ракеты в этой точке, для нахождения траекторий, симметричных относительно прямой, соединяющих центры Земли и Луны, достаточно задавать (и понемногу изменять) ту компоненту скорости ракеты, которая перпендикулярна этой прямой (можно считать, что это вертикальная компонента). Естественно, что начальная точка траектории должна лежать на вышеупомянутой прямой. Наконец, еще один рецепт - периодические траектории будут тем более устойчивыми (т.е. меньше зависеть от начальных данных), чем дальше от Луны будет находиться начальная точка (хотя этот рецепт противоречит требованию удобства наблюдения за лунной поверхностью).
Между прочим, судьба Всеволода Егорова, кажется, была загадочной и таинственной - как утверждает Википедия, он "6 сентября 2001 года пропал без вести в городе Сочи, где имел собственное жильё", это вполне в духе событий романа "Задача трех тел".
Описание траекторий в системе Земля-Луна формально относится к круговой
ограниченной задаче трех тел, поскольку орбита, по которой Луна вращается вокруг
Земли, довольно близка к окружности, но фактически в этом случае достаточно обычной ограниченной задачи (если рассматривать движение космического корабля в той же плоскости, в которой Луна вращается вокруг Земли). Оказывается, что для описания движения в поле тяготения Земли и Луны удобно использовать разные системы координат. Наиболее просто движение выглядит в системе координат, которая вращается вместе с Луной, т.е. в которой Луна неподвижна относительно Земли (такая система называется синодической). Это всегда можно сделать, поскольку сила гравитационного взаимодействия зависит не от конкретного положения тел, а только от расстояния между ними. Более сложной, но и более реалистичной выглядит сидерическая система координат, в которой движение рассматривается относительно неподвижных звезд. В этой системе Луна вращается вокруг Земли по (примерно) окружности с периодом, равным сидерическому месяцу (приблизительно 27 суток 8 часов), в течение которого Луна совершает полный оборот вокруг Земли. В дальнейшем здесь в основном будет рассматриваться движение в синодической системе, кроме нескольких специальных случаев, для которых явно будет отмечено использование сидерической системы. Переход от синодических координат (в которых Луна неподвижна) к сидерическим (в которых Луна вращается вокруг Земли по круговой орбите) осуществляется по формулам:
Далее при построении периодических траекторий в системе Земля-Луна будут использоваться следующие соглашения: среднее расстояние от Земли до Луны (приблизительно 384000 км) будет принято за 1, произведение универсальной гравитационной постоянной G на массу Земли также считается равным 1, поэтому то же произведение для Луны приблизительно равно 1/81.45 (примерно 0.01227747). Вообще, не очень понимаю, как определяют массу космических тел, предполагаю, что как раз через наблюдение за их движением и взаимодействием, т.е. с помощью обратного применения Закона всемирного тяготения. Земля находится в точке (0,0), а Луна - в точке (1,0).
Следующие несколько траекторий для системы Земля-Луна мне удалось построить самостоятельно. Разумеется, все они были давно известны, но в работах по этой тематике не всегда приводятся начальные условия для траекторий, да и просто интересно было самому отыскать их с помощью, по сути, игрушечной программы для графического исследования дифференциальных уравнений.

Названия для этих орбит ("бутылка", "сердце", "полторы восьмерки", "амфора") я тоже придумал сам, они не являются общепринятыми, я просто буду использовать их здесь для удобства
Анимация, изображающая процесс поиска периодической траектории для случая 'бутылки'

Начальные условия для случая 'бутылки'
T0 = 0, T1 = 70
X(T0) = 1.0045
Y(T0) = 0
VX(T0) = 0
VY(T0) = -1.18311976
Системные параметры (массы):
m1 = 0.987722529
m2 = 0.012277471
Другие интересные траектории, возникающие в системе Земля-Луна
Орбита Аренсторфа
Ричард Аренсторф открыл эту орбиту в 1963 году. Формой она немного напоминает "брецель" - своеобразный крендель родом из Германии. Здесь представлены два варианта этой орбиты - долётный (cislunar) и облётный (circumlunar). Начальные данные для долётного варианта взяты из книги: Хайрер Э., Нерсетт С., Ваннер Г. "Решение обыкновенных дифференциальных уравнений", а начальные данные для облётного варианта я подобрал сам

Анимированное изображение движения по долётной и облётной орбитам Аренсторфа

Начальные условия для орбит Аренсторфа
T0 = 0, T1 = 34.130434 (два периода)
долётная облётная
X(T0) = 0.994 1.006
Y(T0) = 0 0
VX(T0) = 0 0
VY(T0) =-2.001585106 -1.181158683
Системные параметры (массы тел):
m1 = 0.987722529
m2 = 0.012277471
Орбита Дэвидсона
Открыта в 1964 году. Эта орбита очень красивая, но очень же и неустойчивая, как пишет о таких орбитах Виктор Себехей в "Теории орбит",
неустойчивы почти во всех смыслах, действительно, их чувствительность к изменениям значения массового параметра (отношения массы Луны к массе Земли) такова, что в некоторых случаях переход от спутника Земли к спутнику Луны, и наоборот, может не произойти, если значение изменится на доли процента

Анимированное изображение движения по орбите Дэвидсона
Здесь изображено два периода

Начальные условия для орбиты Дэвидсона
T0 = 0, T1 = 50
X(T0) = 1.15
Y(T0) = 0
VX(T0) = 0
VY(T0) = 0.0086882909
Системные параметры (массы):
m1 = 0.987722529
m2 = 1-m1
Интересно, что в "Теории орбит" приведены начальные условия для этой орбиты, но с ними построить её у меня не получилось, кое-что пришлось тоже подбирать самостоятельно (а именно - минимальное расстояние от Луны)
Траектория свободного возвращения, моделирование полета Аполлона-13
Траектория свободного возвращения для системы Земля-Луна - это траектория, которая позволяет космическому кораблю, запущенному к Луне, возвратиться на Землю без использования двигателей, только за счет гравитационного взаимодействия с Землей и Луной (под возвращением следует понимать либо посадку на Землю, либо перемещение в точку, расположенную достаточно близко от земной поверхности, из которой уже можно осуществить посадку с небольшими затратами энергии). По-английски такие траектории называются "free-return orbit" или "rescue orbit" (т.е. "орбита спасения"). Для перемещения по такой орбите космический корабль должен оказаться в определенной точке пространства, имея определенную скорость (точнее, определенные величину и направление скорости), далее перемещение к Земле может происходить с выключенным двигателем, т.е. без затрат энергии. Исследование таких траекторий началось еще до первых космических полетов, они рассматривались как средство для подстраховки при полете к Луне на случай какой-либо аварии, после которой использование двигателя космического аппарата будет невозможным или очень ограниченным. Как и прочие орбиты, траектории свободного возвращения бывают долётными (чтобы подлететь к Луне со стороны Земли поближе, а затем вернуться), а также облётными (предусматривающими облёт Луны). Такие орбиты могут иметь разную форму, наиболее известной является "восьмерка", две петли которой окружают Землю и Луну соответственно (для облётных траекторий) или одна из петель окружает Землю, а другая проходит близко от Луны (для долётных траекторий).
Первым космическим кораблем, осуществившим облёт Луны по траектории свободного возвращения, была советская автоматическая космическая станция "Луна-3", в октябре 1959 года передавшая на Землю первые фото обратной стороны Луны.Такие траектории также активно использовались в американской космической программе "Apollo", хотя обычно полеты происходили по комбинированной схеме - полет начинался с достижения какой-либо орбиты вокруг Земли, потом осуществлялся маневр (он назывался Trans-Lunar Injection - TLI), который позволял переместиться на орбиту свободного возвращения для полета к Луне, затем во время полета по этой орбите тестировались все системы корабля, если все было нормально - осуществлялся еще один маневр для перехода на орбиту, более удобную для исследования Луны (орбита свободного возвращения сильно ограничивает места, в которых космический аппарат может прилуниться).
Первыми людьми, увидевшими воочию обратную сторону Луны, был экипаж корабля"Apollo-8", но фактически его орбита тоже была комбинированной. Несмотря на это, реальная орбита "Apollo-8" не очень отличалась от орбиты свободного возвращения в виде "восьмерки", что и было увековечено в памятном медальоне, выпущенном по случаю предстоящего полета (интересно, что автором дизайна медальона был пилот командного модуля "Apollo-8" Джим Ловелл).

Единственным же кораблем программы "Apollo", который облетел Луну по орбите свободного возвращения, был "Apollo-13", и это стало следствием нештатной ситуации, возникшей на борту.
Американский пилотируемый космический корабль "Apollo-13" стартовал 11 апреля 1970 года с космодрома на мысе Кеннеди во Флориде. Экипаж состоял из того самого Джима Ловелла (теперь он был командиром корабля), а также Джона Свайгерта и Фрэда Хейза. Целью полёта была высадка человека на поверхность Луны и проведение научных исследований. Первые двое суток полёта проходили без каких-либо происшествий, но через 55 часов 54 минуты 53 секунды после старта произошел взрыв кислородного баллона и выход из строя двух из трех батарей топливных элементов, которые обеспечивали электропитание в отсеке экипажа командного модуля (он назывался "Odyssey"). Именно тогда Свайгерт произнёс, а Ловелл продублировал фразу "Хьюстон, у нас проблема". От высадки на Луну пришлось отказаться, а экипаж вынужден был бороться за сохранение своих жизней, обеспечивая возвращение на Землю и испытывая при этом большие неудобства от холода и недостатка кислорода. Командный модуль был поврежден взрывом, поэтому для обеспечения маневров пришлось использовать лунный модуль ("Aquarius"), ресурсы которого были крайне ограничены. Тем не менее экипажу удалось благополучно возвратиться на Землю. Драматические события этого полёта показаны в фильме "Apollo-13" с Томом Хэнксом в роли Ловелла.
Я попробовал построить модель траектории, по которой происходил полёт "Apollo-13". Скажу сразу, это очень грубая модель траектории свободного возвращения, кроме того, известно, что космический корабль не все время придерживался этой траектории (после инцидента произошло 4 её корректировки). Тем не менее основные параметры траектории примерно таковы, как указано в статье английской Википедии - минимальное расстояние до Луны, достигнутое в самой дальней точке траектории равно 254 км, использовалось также известное полное время полета, составлявшее без малого 6 суток.
Если в строке поиска Гугла указать "Arenstorf orbit" и осуществить поиск изображений, в большей части результатов будет изображена та самая орбита Аренсторфа в виде "брецеля", которая уже была рассмотрена здесь (или другая её разновидность, с тремя завитками вместо четырех). Однако также в статьях об Аренсторфе говорится о том, что он разработал "орбиту спасения", которая была использована для благополучного возвращения экипажа "Apollo-13" на Землю. Орбита-брецель явно не могла быть для этого использована, поскольку она проходит на довольно значительном расстоянии от Земли. Не могу утверждать наверняка, но для построения орбиты свободного возвращения могла быть использована другая орбита, первооткрывателем которой действительно был Аренсторф. Эта орбита периодическая, но траекторией свободного возвращения является не вся орбита целиком, а её часть (точнее, одна часть в начале периода вместе с одной частью в конце периода). Скромно упомяну, что эту траекторию я тоже сначала нашел сам, с помощью перебора вертикальной составляющей скорости вблизи Луны, а уже потом обнаружил её изображения в статьях соответствующей тематики. Она напоминает цветок с четырьмя лепестками.

Анимированное изображение движения по четырёхлепестковой орбите Аренсторфа

Начальные условия для четырёхлепестковой орбиты Аренсторфа
T0 = 0, T1 = 20
X(T0) = 1.00524
Y(T0) = 0
VX(T0) = 0
VY(T0) = -1.504550898
Системные параметры (относительные массы Земли и Луны):
m1 = 0.987722529
m2 = 0.012277471
Рассматривая анимацию для этой орбиты, нетрудно заметить, что её часть в конце периода вместе с другой частью в начале следующего периода как раз и образуют орбиту в виде "восьмерки" вокруг Земли и Луны.

Так она выглядит в синодической системе координат (которая перемещается вместе
с Луной, т.е. в которой Луна неподвижна).

Анимированное изображение движения по траектории свободного возвращения в синодической системе координат

А такой вид у орбиты в сидерической системе координат

Анимированное изображение движения по траектории свободного возвращения в сидерической системе координат

Видно, что она вполне похожа на изображение орбиты на экране в Центре Управления Полетом на кадре из фильма "Apollo-13"

Начальные условия для орбиты свободного возвращения
T0 = 11.5482, T1 = 13.1985
X(T0) = -0.00793071912
Y(T0) = -0.01670249383
VX(T0) = 10.42031766
VY(T0) = -1.952404189
Системные параметры (относительные массы Земли и Луны):
m1 = 0.987722529
m2 = 0.012277471
Решение в сидерической системе получается с помощью преобразования
Xnew = X*cos(t)-Y*sin(t)
Ynew = X*sin(t)+Y*cos(t)
Разумеется, существует множество разных орбит свободного возвращения. Немного изменяя вертикальную скорость в начальной точке орбиты (напомню, для построения удобно считать, что она является ближайшей к Луне), можно получить орбиты, близкие к рассмотренной выше. Они уже не будут частью большой периодической орбиты, но, пользуясь свойством симметрии решений, можно их достроить до орбит, позволяющих облететь Луну и вернуться.
Виктор Себехей, "Теория Орбит" $8.6.3 - Свойство симметрии решений
В отношении выбора начальных условий для периодических орбит ... нужно сделать несколько дополнительных замечаний. Уравнения движения ограниченной задачи обладают тем свойством, что если
есть частное решение, то
тоже будет решением
Разные близкие орбиты свободного возвращения в окрестности Земли, вместе с периодической (зелёной)


Движение происходит справа налево. Кажется, лучше возвращаться по оранжевым орбитам, по желтым можно улететь неизвестно куда
HALO и NRHO-орбиты, круговая ограниченная задача трех тел
HALO орбиты - это орбиты, связанные с точками Лагранжа в системах двух массивных тел. Их особенностью является то, что тело с пренебрежимо малой массой движется вокруг меньшего из массивных тел, причем движение происходит в плоскости, перпендикулярной той, в которой меньшее тело вращается вокруг большего. Название HALO (далее я попробую объяснить его происхождение) впервые употребил Роберт Фаркуар, который предложил использовать такую орбиту в качестве орбиты для ретранслятора, с которого все время видно как Землю, так и обратную сторону Луны. Ретранслятор был нужен для осуществления связи с участниками миссии Apollo, предполагалось, что космический корабль будет совершать посадку на обратной стороне Луны. В конце концов от идеи посадки на невидимой стороне Луны отказались (корабли Apollo садились на ту сторону Луны, которая обращена к Земле), но изучение таких орбит продолжилось и у них были обнаружены многочисленные полезные свойства, которые можно использовать для исследования Луны.
NRHO (Near Rectilinear Halo Orbit - Близкая к Прямолинейной HALO Орбита) - это подвид HALO орбит, они замечательны тем, что движение космического корабля на отдельных участках очень похоже на прямолинейное. Такие орбиты являются слегка неустойчивыми, но исправление этой неустойчивости требует не очень больших затрат энергии.
В качестве примера рассмотрим так называемую резонансную орбиту NRHO 9:2.

Анимированное изображение движения по орбите NRHO 9:2 в системе координат, в которой Земля неподвижна

Эта орбита - квазипериодическая, а 9:2 означает, что 9 (почти)периодов (оборотов космического корабля вокруг Луны) этой орбиты приходятся на 2 периода (оборота) Луны вокруг Земли. Она связана с коллинеарной точкой Лагранжа , расположенной за Луною на прямой, соединяющей Луну с Землею. Если смотреть с Земли, орбита может проходить как перед орбитой Луны, так и за ней. Это означает, что в определенных точках космический корабль будет находится по ту сторону Луны, которая обращена к Земле, а в других точках он будет с той стороны Луны, которая не видна с Земли, обеспечивая для себя таким образом видимость обратной стороны Луны. Следует также добавить, что эту орбиту предполагается использовать в проекте Lunar Gateway, согласно которому по ней будет вращаться вокруг Луны многомодульная станция.
Чтобы лучше понимать устройство такой орбиты. можно как бы остановить движение, а потом рассмотреть трёхмерное изображение орбиты со всех сторон
Трёхмерное изображение орбиты NRHO 9:2 в системе координат, в которой Земля неподвижна
Здесь изображены два (почти)периода орбиты

Можно также попробовать рассмотреть изображение этой орбиты в координатной системе, в которой Земля и Луна неподвижны

Это изображение помогает понять, почему HALO орбиты так называются - если смотреть на них с Земли, они напоминают лунное гало, оптическое явление, при котором возникает вторичное свечения вокруг источника света.
Трёхмерное изображение орбиты NRHO 9:2 в системе координат, в которой неподвижна Луна (и Земля тоже)

Здесь будет уместно привести начальные условия для орбиты NRHO 9:2
Начальные условия для орбиты NRHO 9:2
T0 = 0, T1 = 13 (чуть больше одного (почти)периода)
X(T0) = 1.021079744
Y(T0) = 0
Z(T0) = -0.18162
VX(T0) = 0
VY(T0) = -0.10176
VZ(T0) = 9.76561018E-7
Массовый параметр - отношение массы Луны к суммарной массе Земли и Луны:
mu = 0.012277471
Начальные условия взяты из диссертации
"Trajectory design and targeting for applications to the exploration program in cislunar space", автор Emily M. Zimovan Spreen. Нужно отметить, что и здесь пришлось немного подгонять эти условия, чтобы всё работало как следует. Подозреваю, что дело в значении массового параметра, автор может пользоваться значением, которое несколько отличается от используемого мною (хотя в диссертации я этого значения просто не нашёл). В любом случае принципиально это дела не меняет.
Заключение
В заключение хочу извиниться за возможные ошибки и неточности. В своё оправдание могу сказать, что космосом я никогда не занимался, космонавтом в детстве быть не мечтал, высоты вообще боюсь. Тем не менее мне интересно было попробовать изучить вопросы освоения космоса с такой чисто теоретической точки зрения (с помощью численного решения дифференциальных уравнений для задачи трёх тел), и рассмотреть результаты именно в виде изображений. При этом не перестаю удивляться необыкновенным красоте и разнообразию решений задачи трёх тел.
И ещё
Вынужден также сознаться, что роман "Задача трёх тел" я не читал, и сериал по роману тоже не смотрел - не очень люблю любую фантастическую литературу. Я прочитал только несколько описаний сюжета, в частности, в Википедии. Тем не менее, я благодарен автору романа, поскольку он стимулировал мой интерес к Задаче
Список литературы
Хайрер Э., Нерсетт С., Ваннер Г. "Решение обыкновенных дифференциальных уравнений"
Виктор Себехей "Теория орбит"
Егоров В.А. "О некоторых задачах динамики полета к Луне"
Ana Hudomal "New Periodic Solutions to the Three-Body Problem and Gravitational Waves"
Emily M. Zimovan Spreen "Trajectory design and targeting for applications to the exploration program in cislunar space"
Комментарии (92)

ifa21rus
25.07.2024 12:50+8Если рассматривать планеты как математические точки (без габаритов) с заданной массой, то ЗТТ численно решается еще. Но Земля и Луна не точки и не идеальные сферы, а Солнце так вообще кружится вокруг центра масс солнечной системы центр которой хотя из "тела" Солнца не выходит, но все же далеки друг от друга. В итоге чтобы считать точно траекторию движения КА надо использовать точные модели планет и их движения. Иначе при возвращении на Землю можно промахнуться и уйти обратно к Луне. А попасть надо было так точно, чтобы сразу начать вход в атмосферу Земли (читай в вязкую тормозную среду) и настолько точно, чтобы не кометой или метеоритом стать, а остаться спускаемым аппаратом. Так что вопрос, как это решал бортовой компьютер Апполона с мозгами не более чем примитивного инженерного калькулятора остается открытым.

belch84 Автор
25.07.2024 12:50+12Так что вопрос, как это решал бортовой компьютер Апполона с мозгами не более чем примитивного инженерного калькулятора остается открытым
Я думаю, что траекторию возвращения расчитывали на Земле, экипаж должен был только выполнять команды ЦУПа. Да и там они не сразу все правильно посчитали:
в ходе перелёта к Земле корабль стал отклоняться от идеальной траектории. Это отклонение было очень незначительным, но постоянным. Его назвали «систематическим дрейфом». Вычисления показали, что в результате дрейфа корабль пройдёт мимо Земли на расстоянии, равном примерно 165 км. Нужно было в третий раз включать двигатель посадочной ступени для ещё одной коррекции.

Wesha
25.07.2024 12:50+5Да и там они не сразу все правильно посчитали:
На Земле всё правильно посчитали, вот только не учли, что охладитель постоянно травит воду.

Radisto
25.07.2024 12:50+5Корректировали орбиту. Точно в неё не попасть ни с каким компьютером, потому что в отличие от модели, как вы уже отметили, и Земля реальная, и Луна, и самое главное, двигатели и корабль тоже реальный, а точность последних не очень-то и высока. Коррекционные двигатели и манёвры для того и есть

Dmitry_Dor
25.07.2024 12:50+19Солнце так вообще кружится вокруг центра масс солнечной системы центр которой хотя из "тела" Солнца не выходит
В среднем ещё как выходит (в т.ч. и для системы Солнце-Юритер)
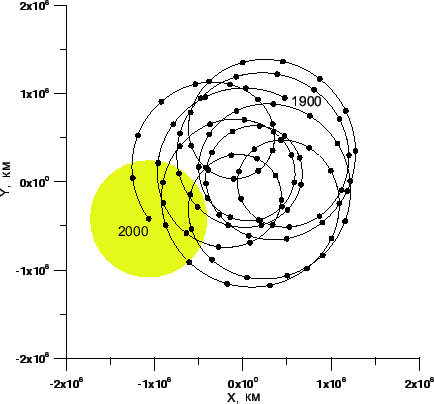
Движение Солнца относительно барицентра солнечной системы в эклиптической системе координат на интервале времени 1900 -- 2000 гг. /zanuda

0x1A4
25.07.2024 12:50+15И для наглядности в виде анимации за период 200 лет:

Сделано в Celestia, где очень точная модель Солнечной Системы

larasage
25.07.2024 12:50Выглядит так, что не Солнце кружится вокруг барицентра, а барицентр крутится в окрестностях Солнца.

muxa_ru
25.07.2024 12:50+2Так что вопрос, как это решал бортовой компьютер Апполона с мозгами не более чем примитивного инженерного калькулятора остается открытым.
Вы смотрите на результат и думаете, что они умнички и у них всё получилось, а им просто могло повезти :)

Dmitry_Dor
25.07.2024 12:50+14Интересный реальный пример круговой ограниченной задачи трех тел в Солнечной системе:
-
Меняющиееся местами на орбите вокруг Сатурна его спутники Янус и Эпиметей

Схема взаимодействия спутников Сатурна Януса и Эпиметея 
Движение спутников Сатурна Януса и Эпиметея относительно друг друга

ArtymQ
25.07.2024 12:50Интересно, много ли еще подобных примеров

Dmitry_Dor
25.07.2024 12:50+4Ну например орбиты Земли и её квазиспутника ("второй луны") Круитни

Относительное движение Земли и Круитни по своим орбитам
-

Travisw
25.07.2024 12:50+1Трудно что ли было записать 18 уравнений для полной задачи трёх тел?

belch84 Автор
25.07.2024 12:50Вы просто так спрашиваете или у вас на примете есть конкретный интересный случай полной задачи трёх тел?

AllKnowerHou
25.07.2024 12:50+1т.е. собственно ссылок на задачу трёх тел не было вообще!
Просто автор такой говорит это, а потом самое интересное - не пишет в частности общую задачу - чем он лучше других сайтов с ссылками на книгу Люцисиня?

belch84 Автор
25.07.2024 12:50+8Знаете, мне стало казаться, что от того, получите ли вы доступ к уравнениям полной задачи, зависит спасение (от) трисолярцев. Вот, пока могу предоставить уравнения в слишком единообразном виде, вместе с таблицей соответствия координат и скоростей точек
Уравнения полной задачи
```(x1,y1,z1), (x2,y2,z2), (x3,y3,z3)
x1 - Y1, y1 - Y2, z1 - Y3, x2 - Y4, y2 - Y5, z2 - Y6, x3 - Y7, y3 - Y8, z3 - Y9
x1' - Y11, y1' - Y12, z1' - Y13, x2' - Y14, y2' - Y15, z2' - Y16, x3' - Y17, y3' - Y18, z3' - Y19
Y1' = Y11
Y2' = Y12
Y3' = Y13
Y4' = Y14
Y5' = Y15
Y6' = Y16
Y7' = Y17
Y8' = Y18
Y9' = Y19
Y10' = 0
Y11' = -c2*(Y1-Y4)/((Y1-Y4)^2+(Y2-Y5)^2+(Y3-Y6)^2)^1.5-c3*(Y1-Y7)/((Y1-Y7)^2+(Y2-Y8)^2+(Y3-Y9)^2)^1.5
Y12' = -c2*(Y2-Y5)/((Y1-Y4)^2+(Y2-Y5)^2+(Y3-Y6)^2)^1.5-c3*(Y2-Y8)/((Y1-Y7)^2+(Y2-Y8)^2+(Y3-Y9)^2)^1.5
Y13' = -c2*(Y3-Y6)/((Y1-Y4)^2+(Y2-Y5)^2+(Y3-Y6)^2)^1.5-c3*(Y3-Y9)/((Y1-Y7)^2+(Y2-Y8)^2+(Y3-Y9)^2)^1.5
Y14' = -c3*(Y4-Y7)/((Y4-Y7)^2+(Y5-Y8)^2+(Y6-Y9)^2)^1.5-c1*(Y4-Y1)/((Y1-Y4)^2+(Y2-Y5)^2+(Y3-Y6)^2)^1.5
Y15' = -c3*(Y5-Y8)/((Y4-Y7)^2+(Y5-Y8)^2+(Y6-Y9)^2)^1.5-c1*(Y5-Y2)/((Y1-Y4)^2+(Y2-Y5)^2+(Y3-Y6)^2)^1.5
Y16' = -c3*(Y6-Y9)/((Y4-Y7)^2+(Y5-Y8)^2+(Y6-Y9)^2)^1.5-c1*(Y6-Y3)/((Y1-Y4)^2+(Y2-Y5)^2+(Y3-Y6)^2)^1.5
Y17' = -c1*(Y7-Y1)/((Y1-Y7)^2+(Y2-Y8)^2+(Y3-Y9)^2)^1.5-c2*(Y7-Y4)/((Y7-Y4)^2+(Y8-Y5)^2+(Y9-Y6)^2)^1.5
Y18' = -c1*(Y8-Y2)/((Y1-Y7)^2+(Y2-Y8)^2+(Y3-Y9)^2)^1.5-c2*(Y8-Y5)/((Y7-Y4)^2+(Y8-Y5)^2+(Y9-Y6)^2)^1.5
Y19' = -c1*(Y9-Y3)/((Y1-Y7)^2+(Y2-Y8)^2+(Y3-Y9)^2)^1.5-c2*(Y9-Y6)/((Y7-Y4)^2+(Y8-Y5)^2+(Y9-Y6)^2)^1.5
```Пожалуйста, сообщите, пригодились ли вам уравнения? Они правильные, это проверено

Refridgerator
25.07.2024 12:50+5У трисоляриан задача на самом деле 4-х тел - три солнца+планета. Вся прочая научная составляющая книги в том же духе - противоречит и физике, и логике.

belch84 Автор
25.07.2024 12:50Нашел в Сети вот такое, но особо не разбирался в деталях

Refridgerator
25.07.2024 12:50+9Если не читали/не смотрели, то и разбирать там нечего. Книга совершенно не стоит разведённого вокруг неё хайпа, и популярность её обусловлена грамотным пиаром и тем, что прочая современная фантастика ещё хуже.
Пара интересных идей там конечно есть, но автор их не смог дожать просто потому, что имеет крайне мутное представление обо всём, что пишет. Он ничего не знает про аналоговые вычислительные машины для решения дифференциальных уравнений. Он ничего не знает про троичную логику, которая более подходяща для человеческого компьютера из элементов, не ограниченных двумя состояниями, а также естественным образом ложится на цивилизацию с 3-мя солнцами с чисто художественной точки зрения (в противовес нашей двоичной с солнцем и луной). Только на этом можно было бы выстроить всю драматургию - начиная от того, что они не умели врать из-за неоднозначности инверсии и заканчивая тем, как двоичная логика победила троичную, а наша цивилизация - их.
А вместо этого там сплошные рояли в кустах.

ifa21rus
25.07.2024 12:50по поводу "двоичных компов". По сюжету книги ЗТТ, как я понял, Трисолярцы устроили видеоигру с привлечением "интеллектуального труда" землян в виде известных персонажей Нюьтон, Энштейн, Тесла и т.д. Как по мне, они через видеоигру шпионили и наши научные наработки сканили, а может что то у себя повторили - тот-же двоичный компьютер. Почему они троичный не повторили? Может китайский писатель-фантаст даже не знал, что такой существует, ну и Трисолярцы тоже остались "с носом": не дотянулись до ЭВМ Сетунь под управлением
академикаБрусенцова.
ksbes
25.07.2024 12:50+4Троичный никаких преимуществ в вычислении задачи трёх те не даст. Единственное его реальное преимущество было - работа с памятью на ферритовых кольцах, у которых как раз намагниченность может быть +,0 и-. Что позволяет существенно экономить столь дорогую память.
Но писателям, конечно, закон не писан - для красного словца можно было бы и подтянуть. Но выглядело бы это столь же не очень, как и то что имеем.

Barnaby
25.07.2024 12:50+1Они использовали видеоигру, чтобы вызывать у ученых эмпатию и склонять на свою сторону.

hK04
25.07.2024 12:50+1Хм, напомню что в игре (созданной для привлечения стороников движения за Трисолирян) описанной в ЗТТ, все же легион людей выступал в качестве вычислительной машины, размахивая двумя флажками. Как антропоморфное существо имея две руки будет размахивать троичной логикой, я представить не могу.
P.S: Главная проблема книги в Сафонах. До них весь набор идей, (кроме конечно изменения реликтового фона, обусловленный разверткой сафона в покрытие земли) в том числе и медленный генетический алгоритм для перебора решений ЗТТ выглядели хотя бы забавно.
Refridgerator
25.07.2024 12:50+1Семафорная азбука двумя флажками передаёт целый алфавит. Видимо, о существовании таковой тоже не все знают.

BugM
25.07.2024 12:50+1Азбука Морзе же. Точка-тире (ай-даа для понимающих). О её существовании знают все.

vconst
25.07.2024 12:50популярность её обусловлена грамотным пиаром и тем, что прочая современная фантастика ещё хуже
Выходит, что я - гений пиара :)
Потому что после окончания перевода, "весь пиар" был из одной этой статьи:Перевод книги Лю Цысинь, «Задача трех тел» https://habr.com/ru/articles/394009/
(да как же в этом редакторе ссылки делать!..)
Выкупили наш перевод только через год_____
Что касается "прочая еще хуже".
За последние десять лет Аберкромби продолжал Земной круг, Гибсон начал цикл Периферийных устройств, Суэнвик продолжил Железных драконов.
И это просто навскидку, первое что вспомнилось, из самого топового.
Grey83
25.07.2024 12:50+1(да как же в этом редакторе ссылки делать!..)
В markdown:
[текст](https://ссылка)
В WYSIWYG отдельная кнопачка есть, но его не юзаю вообще из-за общей глючности и неудобности этого режима.
belch84 Автор
25.07.2024 12:50+2В markdown:
[текст](https://ссылка)Удивительно, это у меня при подготовке публикации работало во всех случаях, кроме вот такого:
Почемут-то редактору не понравился брецель

Так выглядит текст при редактировании 
А так - при просмотре Причем дело не в слове "брецель" - в другом месте ссылка преспокойно вставилась. Возможно, туда попал какой-то символ нехороший, но я его не нашел.
Вообще, замечу, что старый HTML-редактор был намного удобнее всяких визивигов и маркдаунов

Grey83
25.07.2024 12:50+2Вообще, замечу, что старый HTML-редактор был намного удобнее всяких визивигов и маркдаунов
Согласен, пришлось выбирать из оставшихся 2 зол менее злое.
Вообще ещё может пару недель или месяцев назад ссылка вставленная голым текстом превращалась в ссылку, а сейчас так и остаётся текстом. Опять что-то переделали без уведомления пользователей.

Refridgerator
25.07.2024 12:50Вы забыли отметить одного из главных мастодонтов современной фантастики - товарища Зангасту, который и на хабре есть, и в этой теме вроде бы как тоже уже отметился (и да, я в курсе в ваших с ним отношениях, просто не смог удержаться).

konst90
25.07.2024 12:50+1Да там куча проблем.
Например, концепция "черного домена" из третьей книги: мол, если мы каким-то волшебным образом в солнечной системе снизим скорость света ниже скорости убегания, то улететь из такой системы будет невозможно.
Это, естественно, не так. Улететь с планеты или отлететь от звезды можно со сколь угодно малой скоростью, если иметь достаточное количество топлива. Если мы создадим космолёт, который сможет часами создавать тягу и полетим так, чтобы скорость относительно Земли была 1 км/с (ниже первой космической), то за час мы отлетим... Правильно, на 3600 км. И так далее. На орбиту не выйдем, это да, но при достаточном запасе топлива получится вырваться из сферы притяжения, не превышая первой космической скорости.

Zenitchik
25.07.2024 12:50А если скорость света будет ниже скорости убегания, не повернётся ли пространство-время на 90°, чтобы центр Солнца буквально стал будущим?

ksbes
25.07.2024 12:50Не совсем. Это очень нетрадиционный способ появления чёрной дыры, так что традиционная метрика тут плохо работает.
Но в общем и целом не то что Солнце станет будущим, просто оно начнёт для нас, на орбите застынет (а вот внешние пространства наоборот - начнут стремительно эволюционировать), а мы соответственно начнём на него падать - т.к. устойчивой орбиты уже не будет. Так что да в определённом смысле Солнце будет нашим будущим (т.к. мы никак не сможем избежать падения на него). Можно даже сформулировать: текущие состояние Солнца станет нашим отдалённым будущим (т.к. время с нашей точки зрения там застынет и с точки зрения Солнца мы почти мгновенно упадём на него). Но само по себе Солнце будет продолжать существовать всё время падения - мы даже свет от него будем видеть (хоть и тусклый и в радиодиапазоне).
ksbes
25.07.2024 12:50+1И да, улёт на ракете из чёрной дыры - для меня вопрос крайне дискуссионный. Но пока как я понимаю - основная проблема тут: а куда собственно вылетать? Пока будешь лететь - вселенная там за горизонтом событий уже закончится-то!

BugM
25.07.2024 12:50Тут сходится, хотя и с натяжкой.
Скорость Земли на орбите около 30 километров в секунду. Значит нужна скорость больше этой.
Открываем вики, там есть формула. За массу возьмем массу Солнца. Это вполне себе точечная масса, на таких расстояниях. Точность не пострадает.
Калькулятор говорит что он для Солнца около 3 километров. Нам надо 2 орбиты Земли минимум. Чтобы с нормальным запасом. Или 300 миллионов километров. Или в 100 миллионов раз больше чем он на самом деле. Там квадрат в формуле, значит в 10.000 раз меньше скорость света нужна.
300 тысяч километров в секунду делим на 10 тысяч итого 30 километров в секунду.
Прям на тоненького сошлось. Если взять звезду потусклее или добавить возможность подвинуть планету поближе поставив некий экран то можно. В целом для книжки сойдет, порядки величин сошлись.

Tyusha
25.07.2024 12:50+2В "Жизни замечательных людей" про Максвелла меня порразило то, что в те времена ещё не был развит векторрый анализ, и свои уравнения Максвел формулировал, публиковал и решал в скалярной (покомпонентной) форме.

belch84 Автор
25.07.2024 12:50+1Для применения численных методов все равно придется использовать скалярное представление уравнений (если не принимать во внимание какие-нибудь специализированные векторные языки программирования). Но это мое частное суждение, возможно, я отстал от современного положения дел

hK04
25.07.2024 12:50+1Советую прочитать (хотя бы вики) про Хевисайда. Вот кто достоин ЖЗЛ за упрощения у-ей Максвелла.

Refridgerator
25.07.2024 12:50Для меня Хэвисайд герой совсем по другой причине - он смог придумать, как расширить классический мат. анализ для работы с дискретными состояними. Это было гениально. Функция Хэвисайда перевернула моё мировоззрение.

Zangasta
25.07.2024 12:50Интересное совпадение.
Я как раз сейчас пишу фантастический роман, в котором упоминается теория трех тел. По сюжету, космический корабль пришельцев связывается с Землей, с просьбой выполнить математические расчеты. К сожалению, на Земле всего лишь 1936 год и выполнять вычисления приходится вручную.
Буду признателен, если вы заметите неточности или добавите деталей.
Причина катастрофы
Потом пришла чума. Нет, не человеческая чума, а болезнь, поражающая
кремнийорганические процессоры. Природа поражающего фактора осталось неизвестна – но было очевидно, что это прощальный подарок врага, стремящегося завершить уничтожение нашей расы. Мы были высокоразвитой цивилизацией, во всем полагающейся на компьютеры и искусственный интеллект. За несколько часов мы утратили привычные инструменты, потеряли накопленные знания, лишились истории и культуры, рухнув из космического в каменный век. Но даже это не было самым страшным. Оставшись без электроники наш космический корабль отупел, оглох и ослеп.Проблема
Когда мы во второй раз выпали из варпа, уже на окраине вашей солнечной системы, мы сразу заметили странность траекторий транснептуновых объектов – так вы называете крохотные планетоиды, которые вращаются вокруг Солнца на большом расстоянии, намного дальше, чем Нептун или даже Плутон. Их орбиты были слишком эллиптическими, словно их время от времени притягивал некий массивный объект. Сам же объект был невидим – что наводило на мысль об изначальной черной дыре – странном объекте, размером с шарик для пинг-понга, но обладающим массой в несколько сотен земных.
В подобных черных дырах не было ничего интересного или необъяснимого – они массово появлялись в самом начале существования вселенной, когда вещество было настолько плотным, что даже небольшие флуктуации приводили к гравитационному коллапсу. Заметить подобную черную дыру практически невозможно – излучение Хокинга у неё незначительно, а межзвездное пространство слишком бедно на газ и обломки, способные выдать существование дыры стороннему наблюдателю. Конечно, орбиту черной дыры можно было вычислить по искажениям, вносимым в орбиты транснептуновых объектов – но выполнить эти расчеты вручную практически невозможно.
Снова о черной дыре он вспомнил, когда клюнул жареный петух – наблюдая за Землей, пра-пра заметил снижение яркости некоторых звезд: мы приближались к компактному темному газопылевому облаку – глобуле. Подобного не должно было существовать – удерживать холодный газ от рассеивания могло только собственное гравитационное поле, поэтому самые маленькие из глобул имели массу в несколько сотен солнечных. Масса же этой глобулы, судя по искажениям лучей ближайших звезд, не превышала несколько сотен земных – в точности, как у гипотетической черной дыры.
И тут бы ему порадоваться что одной тайны стало меньше – но объект, находящийся в глобуле, очевидно не мог быть черной дырой. Окружающее её газопылевое облако постоянно стремилось вниз, сквозь горизонт событий, вызывая выбросы излучения. Другие же объекты, чисто теоретически способные занять нишу источника гравитации внутри облака, были бы хорошо заметны по излучаемому теплу – что обломки нейронных звезд, что коричневые карлики, излучили его достаточно, чтоб быть обнаруженными нашим телескопом.
Другой, связанной с глобулой проблемой, было увеличение её видимых размеров – мы двигались схожими курсами и пра-пра опасался, что корабль может быть захвачен этим странным объектом. В том, что мы выпали из варпа вблизи глобулы не было ничего удивительного: любая гравитационная аномалия работает как песчаная отмель во времена парусных кораблей. Но от этого было ничуть не легче – не имея энергии для маневров, мы не могли избежать опасного сближения.
Просьба о помощи
Пра-пра поделился своими опасениями с Эбенезером – к тому времени они стали хорошими друзьями.
— Высылай данные, я рассчитаю на досуге, — ответил тот.
Пра-пра посмеялся, помня объем работ. Но данные выслал. Каково же было его удивление, когда он получил через неделю готовый ответ, к которому было приложено описание «Логарифмической линейки» – примитивного устройства с делениями, существенно облегчающего расчеты. Как оказалось, земные математики придумали множество остроумных способов упростить расчеты – формулы сокращенного умножения, матрицы, мнимые числа и прочая, прочая, прочая. Все эти концепции были напрочь забыты нами за ненадобностью – но оказались неожиданно востребованы для ручных расчетов. Эбенезер знал их и был готов поделиться.
Но это было последней хорошей новостью – из рассчитанных данных выходило, что наш корабль будет захвачен объектом и утянут внутрь темного облака – что являлось для нас смертным приговором. По обшивке барабанил поток метеоритов, чья плотность усиливалась с каждым днем.
— Вы должны запустить двигатели, — написал Эбенезер в конце сообщения, — чтоб избежать захвата.
— У нас не хватит энергии, чтоб вырваться из гравитационного поля.
— То, что я не вижу решения, не означает, что его нет. В Европе, на международный математический конгресс собрались все ведущие математики мира. Я передал сыну управление фермой и отправляюсь в Осло! — написал он.
— Спасибо за попытку, дружище – ответил мой пра-пра, — но всё уже бесполезно. Дорога до Европы займет не меньше десяти дней. Когда ты доберешься до конгресса, будет уже поздно – наш корабль погрузится в угольный мешок.
Вы уже догадались что пра-пра ошибался? Он не учел вашего стремительного технического прогресса. Пока его радиограмма летела на Землю из облака Оорта, Эбенезер покупал билет на трансатлантический перелет на первый серийный пассажирский самолет с корпусом из металла – гидроплан «оловянный гусь».
Через сутки он уже был в Осло.
Решение
Уверена, вы сейчас представили себе комичного деревенского фермера с соломой в бороде, который неприкаянно бродит по конгрессу математиков. Конечно, все было совершенно не так. Эбенезер не был деревенщиной. Пожилым да. Крупным и краснолицым – возможно. Увлекающимся и прекраснодушным – вероятно. Но определяло его не это. В первую очередь Эбенезер был ученым, инженером, мыслителем. Одним из умнейших людей своего поколения. То, что он занимался практическим бизнесом не умоляло, а увеличивало его достоинства, добавляя к ним деловую хватку. У собравших на конгресс математиков не было никаких возможностей противостоять его чудовищному обаянию, подкрепленному самой действенной силой во вселенной – силой наличных денег.
— Из ваших данных следует, что это классическая задача трех тел, в заявленном облаке частиц находятся не одно, а два маневрирующих тела, — сказал один из нанятых Эбенезером математиков, некий Норберт Винер, добавив, — Видите ли, по своей основной специализации, я занимаюсь математической теорией броуновского движения. И в теории могу рассчитать вам траекторию движения невидимых тел, основываясь на имеющихся данных наблюдения за крупными фрагментами облака.
— Только в теории?
— Да. На практике это огромный объем расчетов. При этом ваша задача, если я правильно понимаю, еще сложнее – вам нужно рассчитать траекторию движения третьего тела, огибающего первые два.
— Вы можете решить эту задачу?
— Да, мне известно аналитическое решение задачи в виде рядов, но это тоже требует невероятно огромного количества расчетов.
— Пишите формулы. Расчетчиков я найду, — воскликнул Эбенезер.
Главной трудностью следующего этапа миссии, как потом писал Эбенезер, оказался выбор между европейскими политическими течениями, которые присутствовали на конгрессе – коммунистами и фашистами. Как и предполагал Норберт Винер, расчет гравитационного маневра оказался чрезвычайно сложен и требовал полугодового кропотливого труда опытного математика. Но имелся и обходной путь – два математика выполняли расчет за три месяца, шесть математиков – за месяц… Вы уже поняли, куда я клоню. Способностью экстренно мобилизовать несколько сотен математиков обладали только тоталитарные режимы. Что те, что эти не нравились Эбенезеру до колик, что весьма затрудняло выбор. Но тут он прочитал в газетах о принятом в рейхе пакете Нюрнбергских законов и решение стало очевидным.
— Мы можем выполнить требуемые вам расчеты, — сказал эмиссар Советов, к которому обратился Эбенезер.
...
Весь предыдущий день студенты математических и технических вузов России собрались в аудиториях, решая задачу трех тел – разбитую на тысячи параллельных вычислительных потоков, которые сводились и проверялись более опытными математиками. К вечеру решение было найдено – проверено и передано Эбенезеру.
Выйдя на заранее согласованную частоту, он передал пра-пра пакет цифровой информации. Из данных следовало, что наш корабль должен был совершить чудовищный маневр – максимально ускориться и влететь внутрь непроницаемо черной глобулы.
Там мы могли увеличить скорость, совершив облёт одного из скрытых во тьме массивных тел по гиперболической траектории. Полученного довеска, по расчетам, должно было хватить для получения второй космической скорости для глобулы, что позволяло нам навсегда покинуть её негостеприимные окрестности. Попутно, маневр позволял нам развернуть корабль, направляя в сторону Земли.

stan_volodarsky
25.07.2024 12:50+2Черная дыра меннее опасна чем тело той же массы, но которое черной дырой не стало. Например, в чёрной дыре вы погибнете приблизившись к горизонту событий. Приблизившись к телу вы погибнете упав на его поверхность. Второе произойдёт раньше - чёрные дыры самые компактные из объектов той же массы. Пока вы вдалеке от дыры её действие на вас не отличимо от действия массивного тела. Если у вас не нулевой момент импульса, вы никогда не упадёте в черную дыру. Если нет, вы упадёте, но точно также вы упадёте на планету или звезду. Черная дыра - самый безопасный массивный объект в космической навигации. Она не плохо наблюдается, если вы знаете что такое гравитационное линзирование и следите за небом перед кораблём и за изменением направления и скорости корабля.
Вычислительные методы были хорошо развиты и до компьютеров - это правда. Но с появлением компьютеров они стали развиваться ещё интенсивнее. Это кажется странным, но есть причина: если у вас есть быстрый помощник, вы хотите решать задачи большего размера. Если у вас плохие алгоритмы (большое О-большое), ваш в 1000 раз более быстрый помощник не может решить в 1000 раз большую задачу. Например, до середины 20 века люди не умели быстро умножать большие целые числа. Пришел Карацуба и объяснил как это сделать быстрее чем за O(N^2). Еще пример: до калькуляторов не было CORDIC алгоритма для вычисления функций. Все должны были пользовать таблицами, нет таблицы - нет значения функции. Новые функции, новые, быстрее сходящиеся ряды.

Gutt
25.07.2024 12:50+1Например, в чёрной дыре вы погибнете приблизившись к горизонту событий.
Верно только для чёрных дыр менее некоторой массы. Чем больше масса, тем меньше градиент гравитационного потенциала на ГС, и меньше вероятность быть разорванным.
Если у вас не нулевой момент импульса, вы никогда не упадёте в черную дыру.
Почему? Вещество из аккреационных дисков об этом и не подозревает.

BugM
25.07.2024 12:50У них просто недостаточно скорости. При достаточной начальной скорости и вращающейся черной дыре на этих эффектах можно строить классные генераторы просто кидаясь мусором в черную дыру. Импульса у такой черной дыры столько что генератор будет примерно вечным.

stan_volodarsky
25.07.2024 12:50Бросить мусор в чёрную дыру с корабля на круговой орбите - означает что у мусора надо отобрать скорость - первую космическую скорость. Что не легко, например "Паркер" делал семь гравитационных манёвров у Венеры. На орбите Земли у него скорость была 30 км/с, почти всё нужно отобрать, чтобы опустить перигелий и оказаться поближе к
Солнцу. А первая космическая вблизи ЧД куда выше 30 км/с.
BugM
25.07.2024 12:50Немного хитрее. Берем вращающуюся черную дыру. У нее гравитационное поле будет немного искажено. И любое разделившее на границе чд тело будет получать энергию.
Более научно:
Вокруг вращающихся черных дыр существует эргосфера — область, предшествующая горизонту событий. Все тела в эргосфере вращаются вместе с черной дырой.Согласно механизму Пенроуза, если частица делится в эргосфере на два осколка, один из них упадет за горизонт событий, а второй, наоборот, будет выброшен за предел статичности в область, где тела уже не вращаются вокруг черной дыры. При этом энергия выброшенного осколка будет больше, чем энергия изначальной частицы. Это происходит потому, что осколок, упавший в черную дыру, имеет отрицательную энергию. За счет его поглощения скорость вращения дыры снижается, а часть вращательной энергии передается улетевшей частице.
https://nplus1.ru/news/2021/01/19/black-holes-as-energy-source
То есть буквально бросаться мусором в черную дыру. Бросаться надо точно и мусор должен ломаться пополам вовремя. Но это все мелочи.
Там есть скучный вариант с элементарными частицами, но это не интересно и скучно хотя и более эффективно.
Оценки говорят что энергии там валом. Звезды это ерунда все. Сферы Дайсона даже в оптовых количествах это детские игрушки по сравнению с таким генератором .

stan_volodarsky
25.07.2024 12:50Вещество аккреционного диска падает из-за трения внутри диска. Диск не может вращаться как единое твёрдое тело - внутренние слои обгоняют наружные. Возникает трение, вещество диска теряет скорость, нагревается, приближается а горизонту ЧД или к поверхности звезды. Аккреционные диски бывают и у обычных и у нейтронных звёзд. Если вы попадаете в диск, вам не поздоровится - плотная горячая газовая среда. Аккреционные диски равно опасны и у ЧД и у обычных звёзд. Если диска нет, то и рассеять момент импульса некуда. А если вы не теряете момент, вы не можете попасть в ЧД.

vconst
25.07.2024 12:50//удивленно
Поразительно разумное решение для человека, который не понимает даже самых основ физики :)https://habr.com/ru/news/662517/comments/#comment_24291981
В пятидесятые годы в США была разработана электромеханическая самонаводящаяся ракета «Сайдуайндер»
Транзисторов там точно не было. Это было довольно изощренное электромеханическое устройствоЭто даже если не вспоминать, что ты был совершенно уверен в том, что на Луне и Земле длина тормозного пути не будет отличаться :)

Daddy_Cool
25.07.2024 12:50+3А зачем? В статье есть три векторных уравнения - этого достаточно.
Уравнения ЗТТ - это 2-й закон Ньютона - вторая производная по координате (ускорение) равна силе (гравитационной) деленной на массу ускоряемого тела. Скорости получаем дифференцированием.
AllKnowerHou
25.07.2024 12:50Тот комментатор, которому вы написали может комментировать только раз в день, из-за кармы отрицательной

Daddy_Cool
25.07.2024 12:50Ох! У меня тоже отрицательная, но у него круче! )))

AllKnowerHou
25.07.2024 12:50В статье есть три векторных уравнения - этого достаточно
А я вот не понял, лучше бы расписать и еще автору научиться пользоваться Tex языком, чтобы формулы красиво печатать на хабре - статья была бы идеальной

Zenitchik
25.07.2024 12:50Расписывать векторные уравнения по проекциям - это совмещение неприятного с бесполезным. Вот формулы нормально написать, чтобы вектора как вектора выглядели - это да, надо было.

Daddy_Cool
25.07.2024 12:50Справедливости ради, заметим, что:
1. По проекциям бывает полезно расписать для криволинейных координат.
2. В статье вектора выглядят как вектора - прямой жирный шрифт, а скаляры - обычный, при этом наклонный. Это достаточно стандартная запись.
Zenitchik
25.07.2024 12:50+1Справедливости ради, я тоже это понял. Но со стрелочками - ещё стандартнее.

belch84 Автор
25.07.2024 12:50+1еще автору научиться пользоваться Tex языком, чтобы формулы красиво печатать на хабре
Пожалуйста, научите меня!
Интересно, а на каком языке написаны формулы в статье? И что вам для понимания дадут знаки вектора?

voldemar_d
25.07.2024 12:50+2Tex (латинскими буквами) - ключевое слово. Latex еще погуглите.
Хабр этот язык поддерживает.

Grey83
25.07.2024 12:50вот тут в справке про это упоминается: https://habr.com/ru/docs/help/markdown/

belch84 Автор
25.07.2024 12:50вот тут в справке про это упоминается: https://habr.com/ru/docs/help/markdown/
Не очень понимаю смысл ваших советов. В тексте есть формулы, при подготовке текста они выглядят так
$$display$$\begin{aligned} &x_{new} = x\cdot cos(t)-y\cdot sin(t)\\ &y_{new} = x\cdot sin(t)+y\cdot cos(t) \end{aligned}$$display$$Как вы думаете, имею я какое-то представление о TeX или нет? За советы спасибо, конечно, но они какие-то неуместные

Zenitchik
25.07.2024 12:50+3Будем считать массой произведение истинной массы на гравитационную постоянную
Эта величина называется "гравитационный параметр" и обозначается буквой μ .

0x1A4
25.07.2024 12:50+15В начале года EKA утвердило миссию LISA по созданию гравитационной обсерватории, состоящей из трех, развернутых на орбите, лазерных интерферометров. Аппараты выведут на такие гелиоцентрические орбиты, что в любой момент времени они будут составлять равносторонний треугольник с оборотом 1 год.
Вот эта красота:

(кликабельно) А еще на тему задачи трех тел есть ТГ канал (не сочтите за рекламу), где каждый день публикуют симуляцию со случайными параметрами.
Сегодня была такая:


voldemar_d
25.07.2024 12:50обсерватории, состоящей из трех, развернутых на орбите, лазерных интерферометров
https://lisa.nasa.gov/
Будут изучать гравитационные волны.

ksbes
25.07.2024 12:50где каждый день публикуют симуляцию со случайными параметрами.
Приходилось участвовать в организации расчётов по задаче трёх тел - причём именно по вопросу расходимости. И эта задача очень "не любит" близкие сближения или почти столкновения - сразу "рассыпается" по сути. Т.е. "после" часто уже слабо связанно с тем что "до". И вообще рассчитывать большие периоды (и/или большое количество тел) нужно с большой осторожностью и скептицизмом.

stan_volodarsky
25.07.2024 12:50Как контролируются ошибки в решениях? Интервальная арифметика?

ksbes
25.07.2024 12:50+1Ой! Там куча методов была - и интервальная арифметика (хотя я больше интервал использовал как "хранилку", но и считали тоже) и спойлинг ( или веер: слегка подправляем - смотрим разброс) и всякие интегральные методы вроде обратных/зеркальных прогонов. Это давно уже было, но было довольно интересно.
Хотя я там был как технический специалист (из серии: "а теперь со всем этим мы попытаемся взлететь") - так что за теорию особо много сказать не смогу. Но в общем интегральные методы показывали существенно более ранее расхождение, чем поитераторные оценки.И формулы там были посложнее чем в статье: там постоянно шли поправки и контроль по законам сохранения. Без них вся эта байда любит раскручиваться (т.к. суммарный угловой момент в среднем растёт) и, соответственно, разлетаться к чертям (обычно одно тело куда-то буквально "выстреливает")

0x1A4
25.07.2024 12:50И эта задача очень "не любит" близкие сближения или почти столкновения - сразу "рассыпается" по сути.
Вояджеру-2 смогли рассчитать 4 гравитационных маневра у Юпитера, Сатурна, Урана и Нептуна . Розетта - тоже 4 гравитационных маневра. Солнечный зонд Паркер уже совершил 6 грав. маневров у Венеры и в ноябре совершит заключительный. Как-то все это считают.
рассчитывать большие периоды (и/или большое количество тел) нужно с большой осторожностью и скептицизмом.
На сколько понял, системы из 3х массивных тел в большинстве случаев не стабильны и быстро превращаются в систему из двух тел, выбрасывая третье за пределы своего гравитационного влияния.
В звездных системах стабилизирующим фактором являются множественные орбитальные резонансы, некий аналог запутанности на макро масштабах. В Солнечной системе межпланетных резонансов больше, чем планет.

Wizard_of_light
25.07.2024 12:50Зонды с некоторым читерством летают-у них двигатели коррекции поправки и по измерениям с Земли. Тому же "Вояджеру" траекторию поправляли больше десятка раз.

0x1A4
25.07.2024 12:50Это понятно, что коррекция, без нее даже на МКС не слетать, но перед запуском все равно как-то считают все грав. маневры. Там же не так, что вот тут летим до Юпитера, дальше, если повезет, повернем на Сатурн, а там посмотрим как карты лягут.

ksbes
25.07.2024 12:50+1Есть много способов упростить задачу - см. Kerbal Space Program, где свели всё даже не к задаче двух тел, а к орбитальным "рельсам". Но работает - симулирует. Можно даже гравитационные манёвры выполнять!

0x1A4
25.07.2024 12:50Если правильно помню, грав маневры и точки Лагранжа там только с модами, не из коробки. А так про это и говорю, получается, есть рабочая мат модель, которая не рассыпается при таких расчетах.

ksbes
25.07.2024 12:50Ну так точные решения (там эйлера того же) - они вообще абсолютно точные :)
Т.е. да для определённых условий можно именно что упростить задачу, но за это мы платим либо жёсткими ограничениями, либо заведомо внесённой весьма немалой ошибкой - благо хоть можно оценить её порядок.
Например в KSP у спутников нет прецессии орбит под действием гравитации Муны/Кербола, а она составляет до нескольких градусов в сутки. Т.е. через десяток игровых дней расчётная орбита может вообще находится поперёк "реальной". Т.е. по сути как раз решение и "рассыпается"

Wizard_of_light
25.07.2024 12:50+3Там же не так, что вот тут летим до Юпитера, дальше, если повезет, повернем на Сатурн, а там посмотрим как карты лягут.
На самом деле "Вояджер-2" как-то так и летел :)) Основная программа только до Сатурна была рассчитана, а там как повезёт. Правда, не из-за точности расчётов траектории, "Гранд тур" по четырём планетам в принципе был просчитан, и расхождения там были в основном из-за неточностей в импульсах коррекции и определения координат, просто на старте никто не думал, что аппараты полвека работать будут. Уже после пролёта Сатурна инженеры НАСА оценивали вероятность достичь Уран в 65%, а Нептун в 40%.

ArtymQ
25.07.2024 12:50+4Хорошая статья отдельный лайк за визуализацию траекторий тел, классно сделано

Jirabus
25.07.2024 12:50А в книжке то этот крендель решил задачу или нет? Я так и не понял

taujavarob
25.07.2024 12:50В книге странно. Инопланетяне могли двигать свои светила.
И есть такое положение трёх тел, при котором три тела можно выстроить в ряд и тогда они примут устойчивое положение.
Так что землянам надо было передать инопланетянам это "решение" - те многое могут, вполне могут и свои светила выстроить в нужный ряд.
И инопланетянам не пришлось бы тогда лететь к Земле чтобы уничтожить тут нашу цивилизацию.
Но автор книги и сценаристы пошли иным путем.

theWalrus
25.07.2024 12:50В какой именно главе книги написано, что трисолярианцы могли двигать звезды?

taujavarob
25.07.2024 12:50Книгу не читал. Каюсь.
Китайский сериал посмотрел всего две серии и дальше смотреть не стал. Скучный. Каюсь.
Американский же сериал посмотрел весь. Интересный. И в нём инопланетяне дважды пытались передвинуть светила свои, но всякий раз они иногда всё же выстраивались в одну линию и сжигали у них всё на их планете.
Догадаться распределить свои светила в одну линию которая стабильна ни они, ни земляне, которые могли им подсказать это решение, не догадались. Что странно.

theWalrus
25.07.2024 12:50Хм, интересно. Я смотрел сериал тоже, но перемещения звезд не помню.
Сама же книга (как и сериал) лишь первая часть из трилогии. И воспринимать ее как научную фантастику , кмк, не правильно.
Это скорее философские размышления в не очень хорошо проработанном мире.

theWalrus
25.07.2024 12:50В книге другие, более продвинутые товарищи, разрушили одну звезду из трёх вместе с планетой.

shiru8bit
25.07.2024 12:50+4сама по себе задача трёх тел тоже может выглядеть увлекательной в популярном изложении
И далее стена текста размером с экран без разбивки на абзацы. Спору нет, может выглядеть. А может и не выглядеть.

belch84 Автор
25.07.2024 12:50+1Добавил недостававшие уравнения для полной задачи под соответствующий спойлер. По-прежнему интересно было бы увидеть содержательный пример именно полной задачи

ksbes
25.07.2024 12:50Содержательный пример - разрушение двойной системы звёзд при пролёте рядом/сквозь неё третьей звезды.
Ну или просто моделирование ближайшего окружения Солнца - там тоже много чего интересного . Например, Земля может погибнуть и до превращения Солнца в красного гиганта - там "совсем скоро" мимо нас может пролететь звезда и слегка подправить орбиты. Совсем чуть-чуть - там переместить Юпитер в позицию "горячего юпитера", например.

belch84 Автор
25.07.2024 12:50А начальные условия у вас есть? И массы?

ksbes
25.07.2024 12:50В смысле у меня есть? Возьмите хотя бы эти звёзды для начала. Там вроде бы всё хорошо изучено - можно и проверить заодно.

belch84 Автор
25.07.2024 12:50+2Возьмите хотя бы эти звёзды для начала.
Боюсь, моих знаний не хватит, что извлечь из статьи в Википедии начальные данные для уравнений, поэтому я не могу просто взять эти звезды, будто они лежат у меня коробочке


Dmitry_Dor
25.07.2024 12:50+1Совсем чуть-чуть - там переместить Юпитер в позицию "горячего юпитера"
Согласно Grand tack hypothesis это уже почти было ¯\_(ツ)_/¯
Юпитер сформировался недалеко от Frost line, на расстоянии 3,5 а.е. от Солнца, затем мигрировал внутрь на расстояние 1,5 а.е. (при этом сократив часть материала, доступного для формирования Марса), почти стал "горячим Юпитером", но (к счастью для нас) попал в орбитальный резонанс 2:3 с Сатурном, благодаря чему изменил направление миграции, и в итоге оказался на своей нынешней орбиты на расстоянии 5,2 а.е.
/zanuda

kinall
25.07.2024 12:50Пока смотрел на все эти красивые именованные орбиты, мне пришло в голову, что интересно было бы построить график ускорений тел и/или сил, действующих на них. Иначе говоря, если бы это были планеты, то что там происходило бы с силой тяжести?

belch84 Автор
25.07.2024 12:50Это не очень сложно. Вот график зависимости вертикальной скорости от горизонтальной для орбиты Аренсторфа

Для ускорений тоже можно построить, но мне лень выписывать выражения для них - они соответствуют правым частям системы







Daddy_Cool
Очень интересно! Спасибо за статью! Я прочитал книгу Лю Цысиня и тоже увлекся.
Вставлю пару копеек.
Раз копейка. Можно еще упомянуть ряды Зундмана - решение ЗТТ в виде ряда, но... чтобы получить решение с погрешностью 10% надо иногда просуммировать 10^(8e6) членов ряда!
Два копейка. Если кто захочет моделировать - напомню, что надо обеспечить условие нулевого суммарного импульса. Я первый раз задал произвольные массы и скорости и моя система трех тел быстренько улетела за край экрана.