Интегральная оценка пропульсивной системы судна с помощью математического моделирования / forpes.ru

Главная
Интегральная оценка пропульсивной системы судна с помощью математического моделирования

Интегральная оценка пропульсивной системы судна с помощью математического моделирования +6

19.07.2021 00:24

petuhoff 0 1500 Источник

Реферат

Объем морских транспортировок сухих грузов, товаров и энергоносителей продолжает увеличиваться из года в год, в то же время глобальные экологические проблемы, предъявляют повышенные требования к комерческим судам в отношении их эффективности, продуктивности и экологической безопасности. Для удовлетворения строгих и часто противоречивых требований необходимо повышать уровень инженерных решений, и, следовательно, сложность современных пропульсивных систем морских судов. Современный уровень развития технологий обеспечивает множество возможностей для повышения эффективности пропульсивных систем, среди них – средства и устройства для повышения эффективности непосредственно силовой установки, а также оптимизация параметров пропульсивной эффективности судна. Однако обобщенное свойство системы не является суперпозицией свойств компонентов, составляющих данную систему, поэтому конечная цель оптимизации заключается не столько в достижении наибольшей эффективности каждого отдельного компонента, сколько в эффективной интеграции компонентов в единую систему.. Методики моделирования и расчетов пропульсивных систем судов приобретают все более важное значение в решении вышеуказанных комплексных проблем. Особенно, когда становится важной одновременная оценка эффективности, безопасности и надежности пропульсивных систем в реальных условиях эксплуатации и переходных режимах работы.

Методология системного анализа применяется для решения задач комплексного моделирования интегрированной пропульсивной системы судна. Системный анализ — это набор методологий и инструментов для расчетного моделирования динамических процессов, который обеспечивает целостное понимание работы системы и выявления существенных взаимосвязей между подсистемами. Применение системного анализа иллюстрируется путем моделирования пропульсивной установки судна совместно с системой воздушной смазки.

1. Введение

Значительное развитие конструкций пропульсивных установок было вызвано необходимостью уменьшения негативного влияния на окружающую среду, а также необходимостью снижения эксплуатационных затрат. Эволюция потребовала повышения эффективности не только двигателя, но и эффективности движения всего судна в целом. Исторически, введение новых требований регламента сопровождалось развитием конструкций пропульсивных систем судов. На рисунке 1 представлены шаги введения норм и правил и последующие тренды в развитии технологий, связанных с пропульсивными системами судов.

Рисунок 1. Движущие силы и тренды развития судостроения

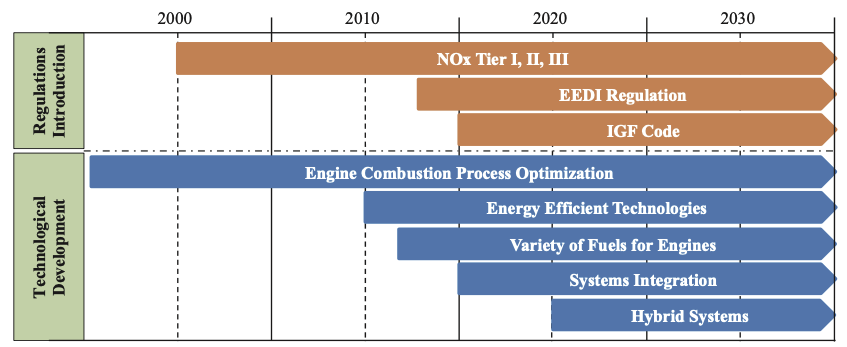
Поршневые двигатели остаются основным источником энергии для пропульсивных установок судов, поэтому эффективность преобразования химической энергии топлива в механическую остается основным фактором улучшения пропульсивных установок с точки зрения расчетного показателя энергоэффективности (Energy Efficiency Design Index – EEDI). Одновременно с этим, жесткие ограничения по выбросам NOxограничивают повышение эффективности процесса сгорания топлива. Это давно известное противоречие в требованиях, в свою очередь, приводит к необходимости прикладывать усилия, в области разработки новых технологий и интеллектуальной интеграции, с целью улучшения конструкций пропульсивных установок судов. Индикатором таких усилий, является появление тренда на создания гибридных систем, которая также включает в себя разработку решений по интеграции систем.

Множество решений по улучшению систем движения уже разработано и представлено на рынке. Совокупность основных подсистем двигателя и существующих решений, которые формируют структуру экосистемы для пропульсивных установок судов представлено на рисунке 2. Однако комбинация различных технологий, применяемых одновременно, может не привести к ожидаемому улучшению из-за наложения противоположных эффектов, или даже привести к снижению общей эффективности в реальных условиях, непредусмотренных проектом. Более того, работа судна, имеет изменяющийся во времени профиль нагрузок, и изменяющиеся шаблоны перемещения грузов (длительность переходов, время загрузки-разгрузки, порты назначения, широты плавания). Все это влияет на энергетическую эффективность интегрированной пропульсивной системы. Таким образом, выбор наиболее подходящего решения и его конфигурации для конкретного судна является нетривиальной задачей.

Рисунок 2. Структура экосистемы пропульсивных установок судов.

Цель проектирования пропульсивной системы судна может быть определена как интеграция различных разнородных механических и электрических компонентов в единую хорошо работающую систему, обеспечивающую максимальную эффективность в широком диапазоне рабочих режимов. С учетом этого интеграция систем представляет собой оценку и оптимизацию поведения переменных состояния системы в разных областях с соблюдением правильного взаимодействия между компонентами. Очевидно, что такая интеграция должна быть выполнена на ранних стадиях проектирования корабля и системы, поэтому расчетное динамическое моделирование технических процессов приобретает большое значение. Однако вследствие сложности интегрированной пропульсивной системы разработка моделирующего инструментария для расчета всей системы в целостном виде не является простой задачей.

2. Инструменты системного анализа

2.1 Базовые принципы метода системного анализа

Давайте начнем с определения системы. По отношению к движению судна система может быть определена как совокупность компонентов и отношений, которые преобразуют входное воздействие в выходное значение для достижения заданной функции. Системный анализ — это метод изучения комплексных систем путем рассмотрения их компонентов и их взаимодействий. Метод системного анализа подразумевает включение нескольких последовательных шагов.

В самом начале должна быть определена область решаемых задач, и таким образом определяются рамки системы. Так, вопрос энергетической эффективности морского транспорта определяет границы системы для конкретных типов и размеров судов. Результаты первого шага устанавливают необходимые условия для второго и последующих шагов, где определяется уровень детализации и набор интерфейсов, необходимый и достаточный для решения поставленных задач. Например, корпус корабля может рассчитываться в детальном трехмерном приближении с помощью 3D гидравлического расчета на Супер ЭВМ, а может – в виде упрощенной характеристики зависимости сопротивления (или момента на винте) от скорости, загрузки и направления движения корпуса судна. Однако, стоит заметить, что на уровне спецификации интересов компоненты должны быть однородны для обеспечения связей между компонентами в единой расчетной схеме модели. (Например, выходные параметры из 3D-модели корпуса, это момент на валу или коэффициенты сопротивления, такие же как у модели в виде упрощенной характеристики).

Последний шаг методологии системного анализа заключается в составлении общей модели системы из иерархически организованных компонентов с выбором определяющих переменных и установлением связи между компонентами системы. Простейший пример состава модели – это пропульсивная установка, включающая два компонента: гребной винт и двигатель, которые взаимодействуют через вал. В результате мы получаем комплексную модель, состоящую из компонентов, описанных в виде математических моделей с требуемой степенью детализации и взаимными интерфейсами для обмена данными. Данная модель обеспечивает динамический расчет процессов в системе.

2.2 Математические основы системного анализа

Основываясь на выбранном уровне детализации, выполняется создание соответствующей математической модели для каждого компонента комплексной модели. Базовые уравнения, представляющие динамического поведение конкретного компонента, основаны на фундаментальных физических законах, эмпирических соотношениях или регрессионных моделях, полученных из реальных данных. Таким образом, в общем случае математическая модель компонента может содержать:

1) Систему обыкновенных дифференциальных уравнений (ОДУ) в форме Коши:

$\left \{ \begin{eqnarray} \frac{dX(t)}{dt} &= f(X(t),U(t),P,t) \\ Y(t) &= g(X(t),U(t),P,t)\\ \end{eqnarray} \right.$

где, X(t),U(t),P - векторы дифференциальных переменных, алгебраических переменных и параметров, соответственно.

2) Систему линейных алгебраических уравнений:

$A \cdot X =K$

где, A,X,K – матрица констант, вектор решения и вектор коэффициентов правой части.

3) Систему нелинейных алгебраических уравнений:

Кроме этого, система может включать компоненты, в которых переменные состояния процесс зависят не только от времени, но и от независимых распределенных аргументов, которые описываются набором нелинейных дифференциальных уравнений в частных производных. Потребность в уравнениях с частными производными может появляться, когда рассматриваются потоки жидкости или процессы теплопроводности. Чтобы включить такие компоненты в структуру модели используется «метод линий» - дискретизация по пространству аргумента, что позволяет преобразовать систему частных производных в систему обычных дифференциальных уравнений.

Например, рассмотрим трансформацию одномерной модели диффузии с заданной границей и начальными условиями, которая описывается следующим уравнением:

$\frac{\partial u}{\partial t}-\alpha\cdot\frac{\partial^2u}{\partial x^2}=0, \ \ \ \ \ \ \ 0\leq x \leq l, \ \ \ \ \ 0\leq t \leq T.$

Используя метод линий, пространственный оператор $\frac{\partial}{\partial x}$ аппроксимируется конечными разностями и получается система полудискретных (дискретных по пространству и непрерывных по времени) обычных дифференциальных уравнений. Вместо одного пространственного уравнения мы получаем набор точек в пространстве, где решаются обыкновенные дифференциальные уравнения с производной по времени:

$\frac{\partial u}{\partial t} \mid_{i}= \frac{\alpha}{\Delta x^2}(u_{i-1}-2\cdot u_i+u_{i+1}), \ \ \ \ \ u_{i}(0)=0, \ \ \ \ \ \ i=2, . . .,N-1$ $u_1=u_1(t), \ \ \ \ \ \ \ u_N=u_N(t), \ \ \ \ \ \ \ \Delta x=\frac{l}{N-1}$

Таким образом полная математическая модель представляет собой систему нелинейных дифференциальных уравнений, дополненную при необходимости начальными условиями.

Кроме того, в структуру модели системы входят не только модели отдельных компонентов, но и дополнительные объединяющие уравнения (коннекторы), которые отражают взаимодействие компонентов. Обычно такие типы уравнений связаны с потоком жидкости, механическими движением (вращательным и поступательным), параметрами электрических систем и сигналами системы управления. Если для первых трех соединений набор переменных (давление, температура, сила, перемещение напряжение и т.п.) определен и фиксирован, то коннекторы к системе управления может содержать любой набор переменных, которые можно получить из датчиков и измерителей.

Набор взаимосвязанных динамических моделей с замыкающими, объединяющими уравнениями (коннекторами) образует модульную и многозадачную структуру для моделирования реальной системы. Следующий шаг в применении системного анализа – это выбор подходящей программной платформы, разработка кода и метода численного решения.

2.3 Программное обеспечение

Для реализации описанного выше системного анализа была выбрана программная платформа «Среда динамического моделирования технических систем «SimInTech» [3]. Данная среда предназначена для детального анализа стационарных и нестационарных процессов в различных технических системах, динамика которых может быть описана системой дифференциальных и алгебраических уравнений, непрерывными и дискретными передаточными функциями, и логическими условиями [4]. SimInTech предоставляет графическую среду для визуального проектирования математической модели в виде функционально-блочных диаграмм, а также для создания видеокадров оператора систем управления.

Преимуществом SimInTech является наличие встроенного языка программирования высокого уровня, обеспечивающего создание новых блоков в единой графической среде. Язык программирования позволяет создавать модели в виде системы дифференциальных и алгебраических уравнений, а также определять входные и выходные переменные непосредственно в графической оболочке без переключения между рабочими пространствами, таким образом пользовательский блок создается быстро просто и наглядно. Другим важным преимуществом перед конкурентами (ближайший аналог Matlab Simulink) является наличие оригинальных методов решения для систем дифференциальных уравнений и алгебраических уравнений, включая неявные методы Рунге-Кутта. Данные методы эффективны для решения жестких систем ОДУ и систем дифференциально-алгебраических систем с порядком больше 1, которые обычно появляются при моделировании комплексных систем, включающих электрические и механические системы [5].

Для моделирования пропульсивной системы судна разработана специальная библиотека блоков в среде SimInTech, что будет показано ниже. Данная библиотека предоставляет базовые строительные блоки в дополнение к широкому набору технических библиотек SimInTech. За счет чего пропульсивная система судна может быть сконструирована в виде иерархической диаграммы из выбранных компонентов. Созданная модель может быть легко реконфигурирована и настроена на проведения численных экспериментов для решения разных задач.

3. Cистемный анализ пропульсивного комплекса судна вместе с системой воздушной смазки

3.1 Описание системы

Рассмотренный реалистичный случай призван продемонстрировать применимость и возможности метода системного анализа для оценки интеграции пропульсивного комплекса судна. Рассматриваемая система – одна из наиболее энергетически эффективных и многообещающих технологий – система воздушной смазки (air lubricationsystem) (ALS), совмещенная с пропульсивным комплексом судна [6]. Воздушная смазка — это эффект снижения сопротивления корпуса судна за счет пузырьков воздуха, подаваемых под днище [7], [8], [9], [10]. Этот эффект прямо пропорционален эквивалентной толщине воздушного слоя:

$t_\alpha = \frac{G_{als}}{B_a \cdot V_s}$

Расход воздуха G_alsопределяет мощность насоса, необходимую для подачи воздуха под днище. Таким образом, для судна с шириной B_a, двигающегося со скоростью V_s,эффективность системы определяется балансом энергии, требуемой для закачки воздуха под днище и снижением расхода энергии на винт, вызванным снижением трения корпуса судна за счет воздуха. Поэтому выбор расхода воздуха определяет общую эффективность системы ALS.

Современные тренды развития дизельных двигателей с турбонаддувом, используемых для для привода движителя судов, направлены на увеличение тепловой эффективности и снижения выброса загрязняющих газов. Как результат этих усилий, эффективность турбокомпрессоров стала избыточна для двигателей, и эта дополнительная энергия может быть использована, после некоторых доработок, для подачи воздуха в систему ALS. Главная проблема такой системы вызвана тем фактом, что достаточная для двигателя подача воздуха из турбокомпрессора возможна только в узком диапазоне режимов. Более того, обычная практика работы судна на низких скоростях и, следовательно, на низкой нагрузке двигателя приводит к дальнейшему ограничению использования турбокомпрессоров двигателя как источника воздуха. В тоже самое время системы рекуперации тепла нашли применение в современных турбокомпрессорах, например, турбогидравлические системы и гибридные системы [11], [12]. Эти системы, если использовать их в режиме реверса для передачи энергии от двигателя к нагнетателю, могут помогать турбокомпрессору и увеличивать подачу воздуха для системы воздушной смазки (ALS) [13].

Согласно методу системного анализа, первый шаг — это определение объема задачи и границы рассматриваемой системы. Настоящая работа посвящена исследованию работы пропульсивной установки судна совместно с системой воздушной смазки, характеристики которой эквиваленты типовому сухогрузу дейветом 60000 тон.

Рисунок 3 показывает рассматриваемую систему ALS, объединенную с двигателем пропульсивной системы. Объем задачи и границы системы:

Оценить совместную работу следующих разнородных систем: корпуса судна оснащенного ALS, двигателя судна как источника воздуха и вспомогательной системы турбокомпрессора для компенсации отбора воздуха из двигателя.
Оценить систему управления и режимы работы.

Рисунок 3. Объем моделирования и границы системы ALS совместно с пропульсивной установкой.

3.2 Создание модели системы

Согласно системному анализу, следующий шаг после установления объема моделирования и границ системы – это определение функциональных взаимозависимостей, которое включает в себя декомпозицию системы в иерархию моделей и компонентов низкого уровня. Учитывая определенные выше границы, пропульсивная система судна считается состоящей из четырех основных функциональных компонентов: корпус судна, винт, двигатель и ALS [14]. Такое разделение позволяет одновременно определить основные взаимодействия между компонентами.

Так винт и двигатель объединены динамикой вращения вала винта, описываемого следующим уравнением:

$2\pi I_e\frac{dn_e}{dt}=Q_e(n_e,p_s,...,t)-Q_p(n_e,V_s,t)$

На основании второго закона Ньютона, баланс сил сопротивления корпуса судна и упора гребного винта, связывающий корпус и винт, определяет изменение скорости корпуса судна.

$M_t\frac{dV_s}{dt}=[1-t_p]\cdot T_p(n_e,V_s,t)-C_r\cdot R_t(V_s,t)$

Где коэффициент трения C_r зависит от толщины воздушного слоя под днищем судна:

$C_r=\frac{R_{als}}{R_t}=f(V_s,t_a)$

Модель системы воздушной смазки обеспечивает распределение потока воздуха от двигателя под днищем судна, что определяет эффективную толщину воздушного слоя t_a. Таким образом модель ALS состоит из трубопроводной системы, регулирующего клапана отбора воздуха из системы двигателя и системы управления.

Функциональная диаграмма на рисунке 4 показывает общие интерфейсы взаимодействия в рассматриваемой между объектом и системой управления.

Рисунок 4. Состав модели пропульсивной установки судна с воздушной смазкой.

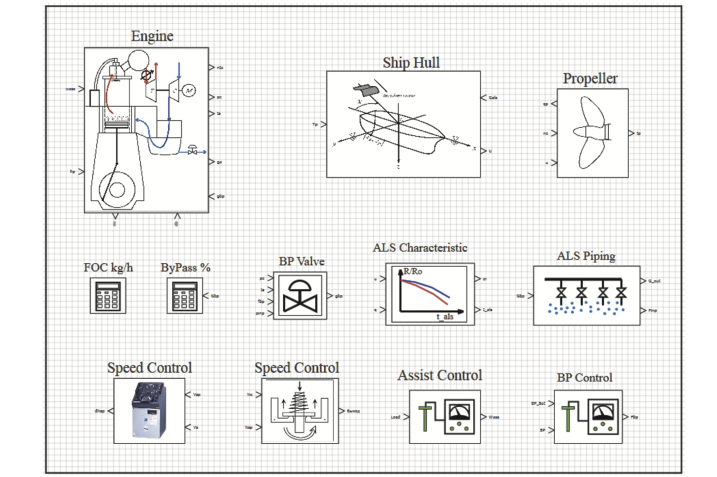
Предыдущие шаги, выполненные в рамках методологии системного анализа, определяют требования к процессу моделирования. На этой стадии каждый функциональный элемент подвергается дальнейшей декомпозиции в структуру иерархических компонентов, а затем каждый компонент описывается математически с требуемой точностью для отображения физических процессов с учетом заданных исходных требований и однородности общей модели системы. В результате выполнения данного шага методики создается библиотека компонентов в выбранной программной платформе. Общий вид библиотеки блоков представлен на рисунке 5. Далее по тексту приводятся примеры детального математического описания функциональных элементов.

Рисунок 5. Библиотека элементов, разработанная в моделирующей платформе.

3.3 Моделирование функциональных элементов

3.3.1 Двигатель

Как уже упомянуто выше основным требованием для математического описания, является достаточная точность этого описания для решения поставленной задачи в заданных границах системы. Модель должна описывать объект с приближением, обеспечивающим интеграцию его в общую функциональную диаграмму, и предоставлять достаточно информации для исследования процессов.

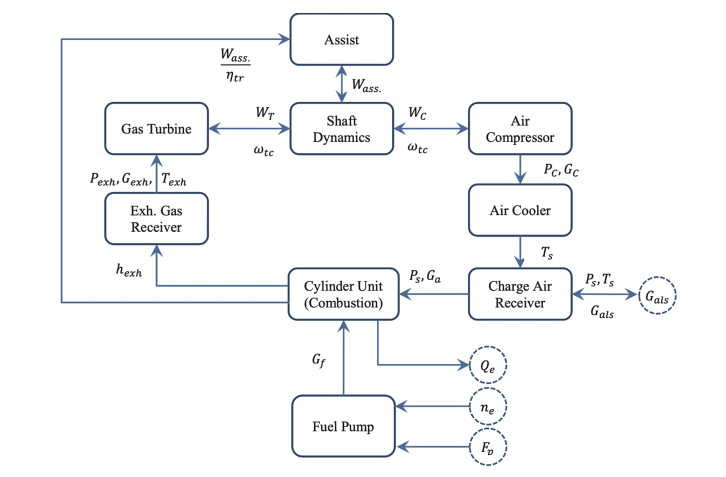
Метод моделирования по средним значениям в последнее время набирает популярность в области динамических расчетов двигателей [15], [16]. Модель, созданная по такому методу (The mean value engine model - MVEM), позволяет рассчитать основные параметры (как термодинамические так и механические) в виде осредненных значений по циклу работы двигателя, пренебрегая изменениями в рамках одного цикла двигателя. Типовая модель MVEM для обобщеного двигателя с турбонаддувом состоит из четырех основных подсистем, которые описывают динамику ресиверов продувочного воздуха и выхлопных газов, блока цилиндров и турбокомпрессора. Кроме этого, с учетом наличия системы воздушной смазки, дополнительно учитывается возможность отбора воздуха и воздушного ресивера и энергия, потребляемая турбокомпрессором. Диаграмма на рисунке 6 показывает связи и потоки данных в модели двигателя.

Ключевые динамические уравнения, необходимые для описания термодинамики двигателя, могут быть получены из законов сохранения энергии, примененных к подсистемам двигателя. Параметры температуры и давления газа в воздушном ресивере и выхлопной системе могут быть получены из закона сохранения энергии и массы. Так, массовый баланс расходов в/из воздушного ресивера определяет изменение давление в нем, согласно соотношению:

$\frac{dP_s}{dt} =\frac{R_aT_s}{V_{a.r}}[G_c-G_a-G_{als}]$

Здесь принимается, что температура воздуха T_s в ресивере постоянна и определяется системой охлаждения. Стоит отметить что расход воздуха в ALS (систему воздушной смазки) G_als определяется открытием или закрытием регулирующего клапана отбора воздуха согласно режимам работы этой системы, как описано далее.

Два дифференциальных уравнения для расчёта массы - $m_{e.r}$ и температуры - $T_{exh}$ в выхлопной системе двигателя, при этом давление рассчитывается из уравнение состояния идеального газа:

$\frac{dm_{e.r}}{dt}=G_a+G_f-G_{exh}$ $P_{exh} =\frac{m_{e.r}R_{exh}T_{exh}}{V_{e.r}}$ $\frac{dT_{exh}}{dt} = \frac{k_e}{m_{e.r}C_{p.e}} \left[h_{exh}(G_a+G_f)-C_{p.e}T_{exh}G_{exh}-\frac{C_{p.e}T_{exh}}{k_e} \frac{dm_{e.r}}{dt}\right]$

В принятом допущении моделирования по средним значениям, двигатель рассматривается как последовательность соединенных сопловых отверстий, соответствующих цилиндрам и турбине турбокомпрессора. Таким образом масса воздуха и выхлопных газов, проходящая через двигатель, может быть описана общим уравнением течения сжимаемой среды через сопло в следующей форме:

$G = \mu\cdot \bar{A}\frac{P_{in}}{\sqrt{R\cdot T_{in}}}\sqrt{2\frac{k}{k+1} \left[\left( \frac{P_{out}}{P_{in}}\right)^{\frac{2}{k}} +\left(\frac{P_{out}}{P_{in}} \right)^{\frac{k+1}{k}}\right]}$

Где $\mu \cdot \bar{A}$ – представляет собой эффективное проходное сечение эквивалентного сопла $P_{in},P_{out}$ - входное и выходное давление.

Массовый расход топлива через двигатель пропорционален позиции клапана подачи от топливного насоса F_p , которое определяется системой управления скорости:

$G_f=z_c \cdot m_{f.c} \cdot F_p\cdot n_e$

Расход воздуха через компрессор G_c в ресивер, может быть вычислен через уравнения изоинтропийной работы, необходимой для сжатия воздуха:

$W_c = \frac{C_{p.a}T_aG_c}{\eta_{ic}}\left( \left( \frac{P_c}{P_a}\right)^{\frac{k_a-1}{k_a}} -1\right)$

Мощность компрессора W_c моделируется как динамическая передача энергии между турбиной и компрессором, в приближении системы первого порядка в следующей форме:

$\frac{dW_c}{dt}=\frac{1}{\tau_{tc}}[W_T-W_c]$

Где W_T – изоэнтропийная работа расширения газа в турбине, определяемая следующим уравнением:

$W_T = C_{p.e}\cdot T_{exh}\cdot G_{exh}\cdot\eta_{iT}\cdot \left[ 1-\left(\frac{P_a}{P_{exh}} \right)^{\frac{k_e -1}{k_e}}\right]$

Основным выходом из модели двигателя, необходимым для интеграции в общую модель, является момент двигателя на валу, определяемый следующим уравнением:

$Q_e=\frac{V_c \cdot z_c}{2 \pi}(IMEP - FMEP)$

Где IMEP и FMEP – это индикаторное среднее эффективное давление цикла и среднее эффективное давление трения, соответственно. FMEP рассматривается как эмпирическая функция, зависящая от скорости ne иположения топливной рейки F_p . IMEP полагается как величина, пропорциональная подаче топлива и коэффициента (также называемого относительной тепловой эффективностью), который отражает нелинейную зависимостью между создаваемым моментом, подачей топлива и подачей воздуха.

$IMEP=\eta_c \cdot IMEP_{MCR}\cdot F_p$ $\eta_c = f \left(\frac{G_a}{G_f} \right)$

В свою очередь, модель двигателя на вход требует следующие переменные: скорость вращения вала, положение топливной рейки и расход воздуха на систему воздушной смазки.

3.3.2 Корпус и гребной винт

Для моделирования корпуса и гребного винта используется упрощенная модель регрессии и (или) интерполяции. Сопротивление воды корпусу судна R_t , представляет собой модель регрессии, полученную из дискретных экспериментальных точек, полученных методом оценки, предложенным в источнике [17]. Полученная сила сопротивления изменяется с использованием коэффициента снижения трения, представленного в уравнении (9).

Модель для тяги T_p и Q_p момента гребного винта восстанавливается с помощью регрессионного анализа коэффициентов, полученных в результате тестирования гребного винта на открытой воде:

$T_p =K_T(J_p)\cdot \rho\cdot n_e^2\cdot D^4_p; \ \ \ \ \ \ \ \ \ \ \ \ J_p=\frac{U_p}{n_e\cdot D_p}$ $Q_p=K_Q(J_p)\cdot\rho\cdot n_e^2\cdot D_p^5; \ \ \ \ \ \ \ \ \ \ \ \ \ \ U_p=[1-w_p]\cdot V_s$

Система воздушной смазки связывает корпус, гребной винт судна и модель двигателя. Количество воздуха, забираемое от компрессора, определяет снижение трения корпуса. И наоборот, мощность на винте и момент на валу влияют на работу двигателя. Эти влияния могут значительно отличаться в зависимости от задачи системы управления движением. Целью управления может быть задание скорости движения судна или задание оборотов двигателя. Таким образом, модель системы управления в общей модели судна играет важную роль в достижении общей эффективности.

3.3.3 Система распределения воздуха

Система распределения воздуха предназначена для управления отбором воздуха от двигателя, транспортировки воздуха от двигателя, расположенного в корме, к распределительным устройствам на корпусе судна, расположенным в носовой части и районе киля. Таким образом, система ALS состоит из регулирующего клапана отбора воздуха и распределительных трубопроводов. Клапан моделируется как дроссель с переменным сечением. Массовый расход описывается моделью течения сжимаемой среды через сопло и определяется следующей зависимостью:

$G_{bp} = \mu\cdot \bar{A}\cdot\frac{P_s}{\sqrt{R_a\cdot T_s}}\sqrt{7\cdot \left( \left[ \frac{P_{bp}}{P_s}\right]^{\frac{2}{k_a}}-\left[ \frac{P_{bp}}{P_s} \right]^{\frac{k_a+1}{k_a}}\right)} ;$ $G_{bp}=G_{als};$

Где: $\mu \cdot \bar{A}$ – представляет собой изменяемое проходное сечение эквивалентного сопла.

$\mu =f(\frac{P_{bp}}{P_s})$ – коэффициент расхода, который представляет собой эмпирическую зависимость, получаемую из данных производителя клапана.

$\bar{A} =f(\theta)$ – проходное сечение в зависимости от положения штока или другого исполнительного механизма, в зависимости от конструкции клапана, управляемого из системы управления.

Поток газа, проходящий через клапан, определяется: 1) площадью раскрытия клапана, 2) давлением в точке отбора в ресивере, 3) давлением на входе в систему распределения воздуха. В свою очередь, когда воздух проходит через разветвлённую систему трубопроводов, происходит потеря давления на трении и возникает задача определить давление после клапана для корректного расчёта расхода воздуха. Осадка корпуса суднаопределяет давление на выходе из системы:

$P_{out}=P_a+\rho\cdot g \cdot_{draft}$

Математическая модель течения газа в трубопроводной системе может быть получена из уравнений Навье-Стокса для сжимаемого газа, рассматривая уравнения сохранения массы, импульса, энергии в применении к контрольному объему (см. рис. 7). Для сокращения уравнения применяются следующие допущения: поток изотермный (T = const); уравнения интегрируются по круглому сечению для снижения размерности. Результирующая система дифференциальных уравнений в частных производных, описывающая поток газа в одномерном приближении, выглядит следующим образом:

$\frac{\partial \rho}{\partial t}+\frac{\partial}{\partial x}[\rho \cdot u]; \ \ \ \ \ \ \ \ \ \ \ P=\rho\cdot R_a \cdot T_a$ $\frac{\partial}{\partial t}[\rho \cdot u]+\frac{\partial}{\partial x}p+\frac{f_r\cdot\rho}{2\cdot d_p}\cdot u\cdot |u|+\rho\cdot g\cdot sin(\alpha) =0$

Рисунок 7. Контрольный объем в трубопроводе

Далее, для включения модели течения газа в общую структуру модели система уравнений в частных производных, описанных выше, должна быть преобразована в систему обыкновенных дифференциальных уравнений. Для этого используем метод линий (MOL method) c дискретизацией по двум точкам и центру, одновременно преобразовываем уравнения к переменным массовый расход и давление.

$\frac{dP}{dt}|_i=-\frac{R_aT_a}{2A\Delta x}[-Q_{i-1}+Q_{i+1}]; \ \ \ \ \ \ \ \ \ \ \ \ \ \ i=2\cdots N-1$ $\frac{dQ}{dt}|_i=-\frac{A}{2\Delta x}[-P_{i-1}+P_{i+1}]-\frac{2f_rR_aT_a}{\pi\cdot d^3_pP_i}Q_i|Q_i|; \ \ \ \ \ \ \ \ \ \Delta x=\frac{l_p}{N-1}$

Давление определяет условия на границах системы со стороны корпуса и ресивера двигателя, расход определяется через зависимость для клапана. Коэффициент трения вычисляется по формуле Колбрук-Уайта в следующем виде:

$\frac{1}{\sqrt{f_r}}= -\frac{2}{3}log\left(\left[\frac{1.547}{R_e\sqrt{f_r}} \right]^{2.8335}+\left[ \frac{k_s}{3.7\cdot d_p}\right]^3\right)$

Благодаря гибкости платформы и возможности создавать свои блоки, модель системы распределения воздуха была создана на языке программирования в виде блока, см. рис. 8

Рисунок 8. Создание модели трубопроводов распределения воздуха в платформе.

3.3.4 Система управления

Одной из главных целей системного моделирования является оценка динамического поведения системы и взаимодействия компонентов. Поэтому интеграция системы управления и процессов ручного управления в общую модель приобретает особую важность.

Из функциональной диаграммы, полученной на шаге композиции, очевидно, что можно выделить четыре контура управления. Первый контур – это обязательный контур для любой пропульсивной установки – контур управления оборотами двигателя. Три других контура связаны с применением системой воздушной смазки судна (ALS). Требуемый поток воздуха для ALS управляется клапаном отбора воздуха от ресивера – это первый контур. В результате работы ALS и отбора воздуха давление в ресивере падает и необходима добавочная энергия от турбокомпрессора для компенсации – это второй контур управления. Третий контур — это управление непосредственно скоростью движения судна путем установления требуемой скорости вращения двигателя. Кроме задачи стабилизации система управления должна обеспечивать возможность непрерывного изменения заданной скорости, задаваемой оператором.

Несколько вариантов алгоритмов управления были разработаны с использованием стандартной библиотеки блоков. Типовые структуры приведены на рисунка 9 a,b,c. Они включают в себя классический PID регулятор, пропорциональный регулятор с обратной связью и пропорционально-интегрирующий регулятор в форме пространства состояний, кроме этого различные нелинейные компоненты были добавлены в управляющие алгоритмы, такие как мертвая зона, ограничитель и т.п.

9.a Классический ПИД регулятор (с встроенной цифровой производной)

9.b Пропорциональный регулятор с изодромной обратной связью

9.с Пропорционально интегрирующий регулятор в форме переменных состояния

3.4 Моделирование динамики интегрированной системы

После разработки индивидуальных компонентов модели, компоновки общей модели, определения всех интерфейсов, модель системы соединяется в единую расчетную схему путем соединения входов с выходами (см. рис.10). Одновременно для упрощения проведения расчётов, анализа и управления самими расчетами создан простой видеокадр управления с пользовательским интерфейсом (см. рис.11). Цель последующего моделирования – определение взаимного влияния друга на друга регуляторов управления.

Прежде чем переходить к обсуждению результатов расчетного моделирования, необходимо отметить важный момент – достоверность модели. Достоверность общей модели обеспечивается точной формализацией процессов, протекающих в субмоделях. Достоверность отдельных моделей в компонентах основывается на хорошо известных и широко используемых методологиях. Так модель двигателя, используемая в статье, была подтверждена путем сравнения с реальными данными эксплуатации и заводскими характеристиками. Результаты сравнения приведены в источниках [13],[16] и [19]. Результаты управления вспомогательной системой турбонагнетателя по наклонной и вертикальной характеристикам подтверждены экспериментально, смотри источник [20]. Достоверность модели корпуса и модели гребного винта, также как эффекта от воздушной смазки, подтверждается численными расчётами и полномасштабными экспериментами. Однако, результаты и данные не могут быть представлены поскольку основаны на проприетарных данных, полученных от верфи, которые не могут быть раскрыты по соглашению.

В процессе моделирования двигательная установка работала на 75% от максимальной долговременной мощности, которая соответствует проектной скорости 13 узлов. Затем клапан отбора воздуха получает команду обеспечить отбор 20% воздуха от номинального расхода на двигатель на данном режиме. После этого два варианта управления установкой движения были использованы:

В первом варианте поддерживались постоянные обороты двигателя. В этом случае скорость судна определяется сопротивлением корпуса судна.
Во втором варианте удерживалась постоянная скорость движения судна. В этом случае меняются обороты двигателя для поддержания заданной скорости.

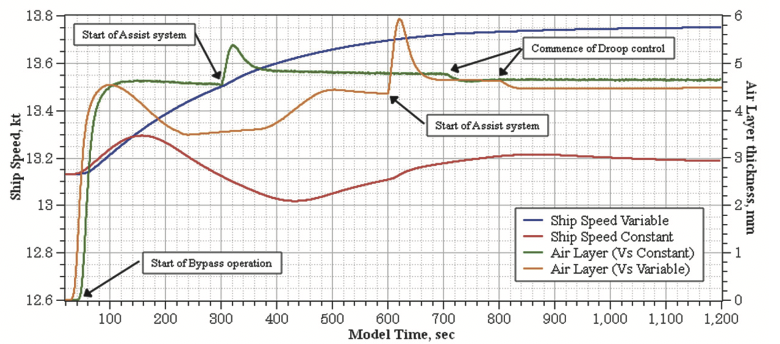
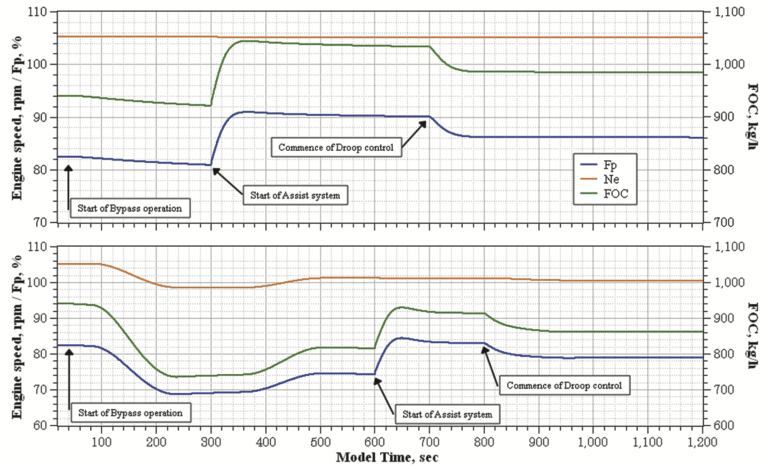
Переходные процессы в различных системах представлены на рисунках 12-14. На рисунках с двумя кадрами, верхний кадр соответствует режиму с постоянными оборотами двигателя, нижний кадр – с постоянной скоростью судна. Стоит отметить, что система позволяет отображать любые параметры модели.

Главная проблема в совместной работе пропульсивного комплекса с системой воздушной смазки корпуса заключается в том, что значительный отбор воздуха вместе со значительным снижением трения, также существенно влияет на эффективность двигателя, за счет снижения давления продувочного воздуха на входе в цилиндры. Это происходит потому, что отбор воздуха работает также, как отбор мощности компрессора, в то время как мощность турбины остается постоянной или даже снижается. Таким образом, для востановления баланса мощности на валу турбокомпрессора необходим дополнительный подвод энергии. Дополнительную энергию обеспечивает вспомогательная система, подключенная к турбокомпрессору. Регулятор вспомогательной системы настроен на поддержание давления воздуха после турбокомпрессора на заданном проектном уровне. При таком астатичном режиме управления дополнительные затраты энергии прямо пропорциональны расходу воздуха на систему воздушной смазки, и желательный уровень экономии энергии за счета ALS может быть не достигнут. Как было показано в [13] и подтверждено экспериментально в [20], решение данной проблемы в использования наклонной характеристики регулятора – поддерживаемое давление продувочного воздуха ниже чем требуемое на данном рабочем режиме. Эффект от применения наклонной характеристики регулятора отчетливо виден на рисунках 13 и 14a, где представлены энергия вспомогательной установки и общий расход топлива.

Рисунок 12. Скорость судна и толщина воздушного слоя

Рисунок 13. Расход отбора воздуха и вспомогательная энергия

Рисунок 14.A Скорость двигателя, топливная рейка и расход топлива (FOC)

Рисунок 14.B Скорость турбокомпрессора и давление нагнетания

Заключение

В данном отчете представлена общая схема методологии системного анализа. В исследовании указанная методология применялась, для оценки интеграции пропульсивной установки судна и системы воздушной смазки (ALS). Разработанная модель обеспечивает понимание поведения системы за счет расчётного моделирования комплексных физических процессов с учетом реального взаимодействия компонентов в системе.

Разработанная многокомпонентная модель, представленная в работе, подходит для синтеза интегральных систем пропульсивной установки судна и их расчетного моделирования в стационарных и динамических режимах работы, а также для оптимизации с использованием тех же моделей компонентов. Модель полностью параметризованная, а ее структура может быть легко модифицирована для исследования иного круга проблем, также при необходимости возможно добавление новых компонентов. Например, могут быть достаточно просто добавлены модели гребного винта, изменяемого шага или регулировочного клапана турбокомпрессора. Можно также вместо простого потока энергии для турбокомпрессора выполнить моделирование с учетом электрической и механической частей агрегатов для анализа переходных процессов в системе передачи энергии и управления. Также модель корпуса можно усложнить для учета динамики реального моря.

Последнее, но не менее важное: созданная структура модели, очень хорошо подходит для использования в модельно-ориентированном проектировании, например для виртуальных испытаний и цифровых двойников. Цифровые двойники обеспечивают связь данных реального мира с системной моделью, фокусируясь на различных аспектах работы системы в реальном времени и в динамических режимах в условиях реальной эксплуатации.

Литература

Список литературы

1) Dimopoulos, G.G., Kakalis, N.M.P., 2010, An Integrated Modelling Framework for the Design, Operation and Control of Marine Energy Systems, Proc. of the CIMAC Congress, Paper No.: 154

2) Stefanatos, I., Zymaris, A., et al., 2016, Assessment of LNG Carriers Electric Propulsion Configuration via Process Modelling, Proc. of the CIMAC Congress, Paper No.: 177

3) SimInTech website http://simintech.ru/?page_id=398 (last accessed on February 2018)

4) Kozlov, O.S., Skvortsov, L.M., 2016, MVTU software package in scientific research and applied developments, Math Models Comput Simul, Vol. 8, Issue 4, pp358-368

5) Skvortsov, L.M., Kozlov, O.S., 2014, Efficient implementation of diagonally implicit Runge-Kutta methods, Math Models Comput Simul, Vol. 6, Issue 4, pp415-424

6) Fukuda, T., 2015, Air lubrication method of hull using scavenging air of large marine engine, (in Japanese), Journal of the Japan Institute of Marine Engineers, Vol 50(2), pp89-92

7) Kodama, Y., Kakugawa, A., et al., 2000, Experimental study on microbubbles and their applicability to ships for skin friction reduction, Int. Journal of Heat and Fluid Flow, Vol.21, Issue 5, pp582-588

8) Kato, H., Kodama, Y., 2003, Microbubbles as a skin friction reduction device – a midterm review of the research, Proc. the 4th Symposium on Smart Control of Turbulence

9) Kodama, Y., Takahashi T., et al., 2005, Practical application of microbubbles to ships – Large scale model experiments and a new full-scale experiment, Proc. of the 5th Osaka colloquium

10) Hinatsu, M., 2013, Recent Activity on the Energy Saving for Ships Using Air Lubrication Method, (in Japanese), Japanese Journal on Multiphase Flow, Vol. 27

11) Sakairi, N., Tanaka, I., et al., 2013, Development of Turbo Hydraulic System on Large Marine Diesel Engine, Proc. of the CIMAC Congress, Paper No.: 146

12) Ono, Y., 2013, Solutions for better engine performance at low load by Mitsubishi turbochargers, Proc. of the CIMAC Congress, Paper No.: 15

13) Bondarenko, O., Fukuda, T., 2015 Consideration of Propulsion Engine Operation in Combination with Ship Hull Air Lubrication, Far Eastern Federal University: School of Engineering Bulletin, Vol.1, pp22-31

14) Bondarenko, O., Kashiwagi, M., 2010, Dynamic Behaviour of Ship Propulsion Plant in Actual Seas, Journal of the Japan Institute of Marine Engineers, Vol 45, pp76-80

15) Theotokos G.P., 2009, A Comparative Study on Mean Value Engine Modeling of Two-Stroke Marine Diesel Engine., In Proc.: The 2nd International Conference on Maritime and Naval Science and Engineering

16) Bondarenko O., Fukuda T., et al., 2013, Development of Diesel Engine Simulator for Use with Self-Propulsion Model. Journal of the Japan Institute of Marine Engineers, Vol. 48, pp 98-105

17) Holtrop, J. and Mennen, G.G.J., 1982, An approximate power prediction method. Int. Shipbuilding Progress, 29(335), pp166-170

18) Oosterveld, M.W.C., Oossanen, P.van, 1972, Recent Developments in Marine Propeller Hydrodynamics, International Jubilee Meeting 40th Anniversary of the Netherlands Ship Model Basin, NSMB Publication No. 433

20) Fukuda, T., Bondarenko, O., 2018, Combination of Propulsion Engine with Air Lubrication System for Ultimate Ship Efficiency, Journal of the Japan Institute of Marine Engineers, Vol. 53, No. 3 (to be published)