Нахождение точки пересечения двух отрезков.
Имеем 2 отрезка {P0,P1} и {P2,P3}, где P0,P1,P2,P3 точки на плоскости. Будем обозначать x y координаты точки P как P.x и P.y
Имеем координаты 4 точек в массиве P(0..3) структуры point(x float, y float):
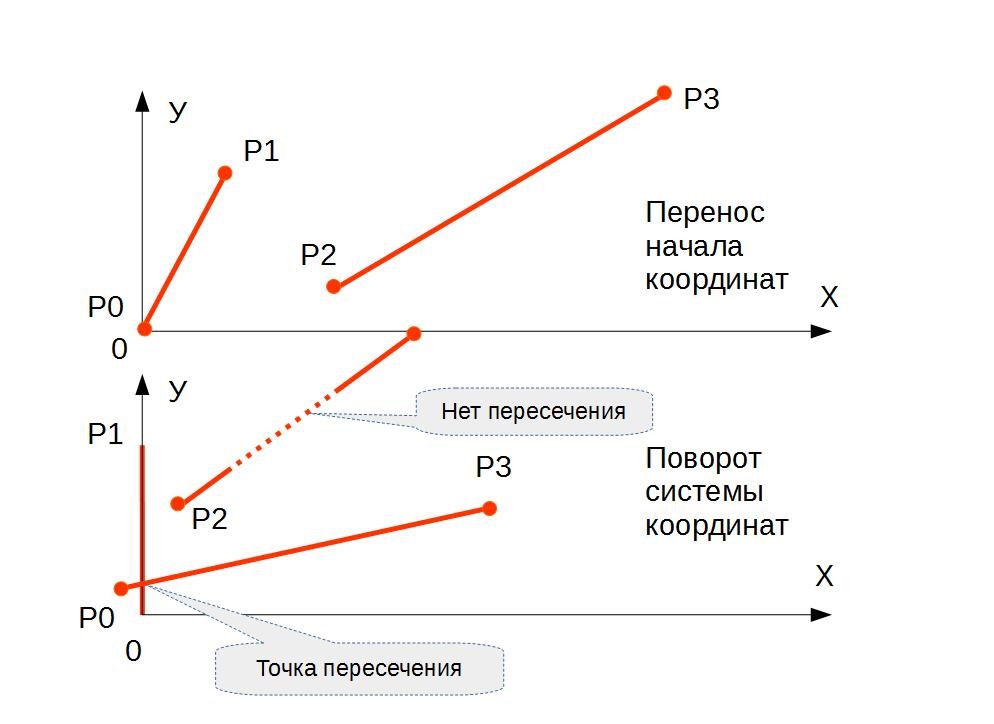
Шаг 1 — Перенос начала координат.
Запомним координаты точек P в дополнительном массиве P_copy. Перенесем начало системы координат в точку P0 и пересчитаем координаты точек:
P_copy = P
P(0).x = 0 ; P(0).y = 0
for ii = 1 to 3
P(ii).x = P(ii).x - P_copy(1).x ; P(ii).y = P(ii).y - P_copy(1).y
next
Шаг 2 — Поворот начала координат
Повернем систему координат так, чтобы отрезок {P0,P1} принял вертикальное положение (лег на ось Y). Вычислим длину отрезка {P0,P1} как:
L1 = SQRT ( (P(1).x)^2 + (P(1).y)^2 )
Синус и косинус угла alfa поворота осей координат:
если L1 > 0
sin_alf = sin(alfa) = P(1).x / L1
cos_alf = cos(alfa) = P(1).y / L1
если L1 = 0 // точку не поворачиваем
sin_alf = 0
cos_alf = 1
Cнова пересчитываем координаты точек P1,P2,P3:
P(0).x = 0 ; P(0).y = 0 // Точка P0 не поворачивается, она в начале координат
P(1).x = 0 ; P(1).y = L1
P(2).x = P(2).x * cos_alf - P(2).y * sin_alf
P(2).y = P(2).y * cos_alf + P(2).x * sin_alf
P(3).x = P(3).x * cos_alf - P(3).y * sin_alf
P(3).y = P(3).y * cos_alf + P(3).x * sin_alf
Шаг 3 — Поиск точки пересечения отрезков.
Запишем уравнение отрезка {P2,P3} и найдем точку его пересечения CR с осью Y:
P23X = P(2).x + ( P(3).x - P(2).x ) * beta
P23Y = P(2).y + ( P(3).y - P(2).y ) * beta
где 0 <= beta <= 1
В точке CR пересечения отрезка {P2,P3} с осью Y:
P(2).x + ( P(3).x - P(2).x ) * beta =0
Далее возможны 2 варианта в зависимости от значения P(3).x — P(2).x:
1 вариант:
если ( P(2).x - P(3).x ) <> 0 // отрезок {P2,P3} не вертикален
beta = P(2).x / ( P(2).x - P(3).x )
если beta >= 0 и beta <= 1 // отрезок {P2,P3} пересекает ось Y
CR.x = 0
CR.y = P(2).y + ( P(3).y - P(2).y ) * beta
//условие пересечения отрезков:
0 <= CR.y <= L1
2 вариант:
Если P(2).x = P(3).x, то это означает, что отрезок {P2,P3} вертикален и параллелен отрезку {P0,P1}. Пересечение отрезков возможно только если второй отрезок {P2,P3} тоже лежит на оси Y, и один из его концов лежит в первом отрезке {P0,P1} (или касается) или отрезок {P2,P3} накрывает {P0,P1}. Будем считать что для результата нам достаточно одной точки. Это будет одна из точек P0..P3.
Условия:
P(2).x = P(3).x = 0 // второй отрезок {P2,P3} вертикален b лежит на оси Y.
и // условие пересечения:
P(2).y >= 0 и P(2).y <= L1 // P2 внутри отрезка {P0,P1}
-> CR = P_copy(2) // результат выбираем вершину P2
или
P(3).y >= 0 и P(3).y <= L1 // P3 внутри отрезка {P0,P1}
-> CR = P_copy(3) // результат выбираем вершину P3
или
P(2).y < 0 и P(3).y > L1 // отрезок {P0,P1} внутри отрезка {P2,P3}
или
P(3).y < 0 и P(2).y > L1
-> CR = P_copy(0) // // результат выбираем вершину P0 (или P1)
)
Шаг 4
Если точка пересечения CR найдена по варианту 1 шага 3, то ее координаты пересчитываем для исходной системы координат. Используем переменные сохраненные на 1 и 2 шаге. Поворот на угол -alfa:
CR.x = CR.x * cos(-alfa) + CR.y * sin(-alfa) = CR.x * cos_alf + CR.y * sin_alf
CR.y = CR.y * cos(-alfa) - CR.x * sin(-alfa) = CR.y * cos_alf - CR.x * sin_alf
Перенос обратно:
CR.x = CR.x + P_copy(0).x
CR.y = CR.y + P_copy(0).y
Если точка пересечения CR найдена по условию 2 шага 3 пересчет координат не нужен. Пример кода на golang под катом. Golang ом я только балуюсь, поэтому к коду прошу быть снисходительным. Код можно запустить на golang.org:
// line_cross project main.go
package main
import (
"fmt"
"math"
)
type point struct {
x float64
y float64
}
func main() {
var P [4]point
var P_copy [4]point
var L1, sin_alf, cos_alf, wsp1, wsp2, beta float64
var flag_cross bool
var CR point
// исходные данные x y координаты точек
P[0].x = 1.0
P[0].y = 2.0
P[1].x = 10.0
P[1].y = 20.0
P[2].x = 3.0
P[2].y = 9.0
P[3].x = 9.0
P[3].y = 3.0
// шаг 1
P_copy = P
fmt.Println("Исходные данные:")
for ii := 0; ii < 4; ii++ {
fmt.Println(" p", ii+1, " x", P_copy[ii].x, " y", P_copy[ii].y)
}
P[0].x = 0
P[0].y = 0
for ii := 1; ii < 4; ii++ {
P[ii].x = P[ii].x - P_copy[0].x
P[ii].y = P[ii].y - P_copy[0].y
}
// шаг 2
L1 = math.Sqrt(P[1].x*P[1].x + P[1].y*P[1].y)
if L1 > 0 {
sin_alf = P[1].x / L1
cos_alf = P[1].y / L1
} else {
sin_alf = 0
cos_alf = 0
}
P[1].x = 0
P[1].y = L1
for ii := 2; ii < 4; ii++ {
wsp1 = P[ii].x*cos_alf - P[ii].y*sin_alf
wsp2 = P[ii].y*cos_alf + P[ii].x*sin_alf
P[ii].x = wsp1
P[ii].y = wsp2
}
//шаг 3
flag_cross = false
if P[2].x-P[3].x == 0 { // отрезок {P3,P4) параллелен {P0,P1)
if P[2].x == 0 && P[3].x == 0 {
switch {
case P[2].y >= 0 && P[2].y <= L1:
flag_cross = true
CR = P_copy[2]
case P[3].y >= 0 && P[3].y <= L1:
flag_cross = true
CR = P_copy[3]
case (P[2].y < 0 && P[3].y > L1) || (P[3].y < 0 && P[2].y > L1):
flag_cross = true
CR = P_copy[0]
}
}
} else {
beta = P[2].x / (P[2].x - P[3].x)
if beta >= 0 && beta <= 1 {
CR.x = 0
CR.y = P[2].y + (P[3].y-P[2].y)*beta
if CR.y >= 0 && CR.y <= L1 {
//шаг 4
// пересчет координат
flag_cross = true
wsp1 = CR.x*cos_alf + CR.y*sin_alf
wsp2 = CR.y*cos_alf - CR.x*sin_alf
CR.x = wsp1
CR.y = wsp2
CR.x = CR.x + P_copy[0].x
CR.y = CR.y + P_copy[0].y
}
}
}
if flag_cross {
fmt.Println("Точка пересечения: х =", CR.x, " y=", CR.y)
} else {
fmt.Println("Отрезки не пересекаются !")
}
}
Комментарии (19)

ibrin
29.09.2015 19:49+7Решаем алгебраически: y=kx+b, P0(x1,y1), P1(x2,y2), P2(x3,y3), P3(x4,y4).
k1=(y1-y2)/(x1-x2)
k2=(y3-y4)/(x3-x4)
b1=(y1x2-y2x1)/(x2-x1)
b2=(y3x4-y4x3)/(x4-x3)
Пересечение прямых:C(x,y)
x=(b2-b1)/(k1-k2)
y=(b1k2-b2k1)/(k2-k1)
Перечение отрезков:
(min(x1,x2)<=x<=max(x1,x2)) && (min(x3,x4)<=x<=max(x3,x4)) && (min(y1,y2)<=y<=max(y1,y2)) && (min(y3,y4)<=y<=max(y3,y4))
SemenovVV
30.09.2015 09:00Каким будет ваше решение если x1 =x2 или x4 = x3 или k1 = k2 ( деление на 0 )?

ibrin
30.09.2015 11:44Это же общее решение. Проверить входные данные и промежуточные результаты можно и самостоятельно. Всего 4 варианта:
1. Отрезок Р0Р1 вырождается в точку
2. Отрезок Р2Р3 вырождается в точку
3. Прямые параллельны k1=k2 b1<>b2 — нет решения
4. Прямые совпадают k1=k2 b1=b2 — возможно множество решений
SemenovVV
30.09.2015 13:401. Отрезок Р0Р1 вырождается в точку
если это вариант x1 =x2 и y1<>y2
Отрезок не вырождается, отрезок вертикален, k1 = бесконечности
4. Прямые совпадают k1=k2 b1=b2 — возможно множество решений
Решений может и не быть. Отрезки могут лежать на одной линии и не пересекаться.
Я видел задачу в минимизации числа операций ( вычислений сравнений) алгоритма. Уверен это можно сделать лучше чем у меня.
Мне кажется, если прописать ваш алгоритм со всеми проверками, операций не станет меньше.
ibrin
30.09.2015 18:33+1Решение со всеми проверками:
#!/usr/bin/python print "Hello, Python!" # input data x1=0.0 y1=0.0 x2=0.0 y2=0.0 x3=0.0 y3=0.0 x4=0.0 y4=0.0 # logic if (x1<>x2) and (x3<>x4): k1=(y1-y2)/(x1-x2) b1=(x2*y1-x1*y2)/(x2-x1) k2=(y3-y4)/(x3-x4) b2=(x4*y3-x3*y4)/(x4-x3) if k1<>k2: x=(b2-b1)/(k1-k2) y=(k2*b1-k1*b2)/(k2-k1) if (min(x1,x2)<=x<=max(x1,x2)) and (min(x3,x4)<=x<=max(x3,x4)) and (min(y1,y2)<=y<=max(y1,y2)) and (min(y3,y4)<=y<=max(y3,y4)): print "norm-1 C(",x,";",y,")" else: print "none" else: if b1==b2: if max(min(x1,x2),min(x3,x4))<min(max(x1,x2),max(x3,x4)): print "norm multiple solution C(",max(min(x1,x2),min(x3,x4)),"..",min(max(x1,x2),max(x3,x4)),";",max(min(y1,y2),min(y3,y4)),"..",min(max(y1,y2),max(y3,y4)),")" else: if max(min(x1,x2),min(x3,x4))==min(max(x1,x2),max(x3,x4)): print "norm-2 C(",max(min(x1,x2),min(x3,x4)),";",max(min(y1,y2),min(y3,y4)),")" else: print "none" else: if ((x1==x2) and (x3<>x4)) or ((x1<>x2) and (x3==x4)): if x3<>x4: k=(y3-y4)/(x3-x4) b=(x4*y3-x3*y4)/(x4-x3) x=x1 if x1<>x2: k=(y1-y2)/(x1-x2) b=(x2*y1-x1*y2)/(x2-x1) x=x3 y=k*x+b if (min(x1,x2)<=x<=max(x1,x2)) and (min(x3,x4)<=x<=max(x3,x4)) and (min(y1,y2)<=y<=max(y1,y2)) and (min(y3,y4)<=y<=max(y3,y4)): print "ex-1 C(",x,";",y,")" else: print "none" else: if (x1==x2) and (x3==x4) and (x1==x3): if max(min(y1,y2),min(y3,y4))<min(max(y1,y2),max(y3,y4)): print "ex multiple solution C(",x1,";",max(min(y1,y2),min(y3,y4)),"..",min(max(y1,y2),max(y3,y4)),")" else: if max(min(y1,y2),min(y3,y4))==min(max(y1,y2),max(y3,y4)): print "ex-2 C(",x1,";",max(min(y1,y2),min(y3,y4)),")" else: print "none" else: print "none"
MrShoor
01.10.2015 06:07+2Чйорт побери. Лучше бы вы не показывали свое решение. Оно же не подлежит поддержке… я даже знаю на какой сайт можно такое отправлять.

ibrin
03.10.2015 13:50цеж прототип! вычисления занимают отсилы 10 строчек, а всё остальное частные случаи, типа частичного совпадения отрезков, что в общем-то и не пересечение, а общие точки имеются.

SemenovVV
07.10.2015 15:04проверьте, плиз, параллельные отрезки
например:
x1=1.0 y1=1.0 x2=5.0 y2=5.0 x3=3.0 y3=4.0 x4=4.0 y4=5.0
я не знаком с питоном, запускал на Coding Ground www.tutorialspoint.com/execute_python_online.php
не увиделprint "none"
ibrin
07.10.2015 16:33мой косяк, забыл else print «none» для k1=k2 & b1<>b2
высылаю патч:
@@ -31,6 +31,7 @@ print "norm-2 C(",max(min(x1,x2),min(x3,x4)),";",max(min(y1,y2),min(y3,y4)),")" else: print "none" + print "none" else: if ((x1==x2) and (x3<>x4)) or ((x1<>x2) and (x3==x4)): if x3<>x4:
спасибо за тесты!

ibrin
07.10.2015 16:41Это мой первый код на питоне и патч кривой.
Вот правильный:
@@ -31,6 +31,8 @@ print "norm-2 C(",max(min(x1,x2),min(x3,x4)),";",max(min(y1,y2),min(y3,y4)),")" else: print "none" + else: + print "none" else: if ((x1==x2) and (x3<>x4)) or ((x1<>x2) and (x3==x4)): if x3<>x4:

0serg
29.09.2015 21:38+1Это неэффективное решение стандартной и хорошо изученной задачи «в лоб». Учебная задачка для любого приличного студента, какой смысл о ней писать? Есть изящные, красивые и эффективные решения, лучше бы о них написали

PapaBubaDiop
29.09.2015 23:25Особенно огорчает использование дорогих cos(x) и sin(x), совсем не ценят такты молодые ребята…

SemenovVV
30.09.2015 08:47Согласен, задача стандартная, написал только как вариант для ранее опубликованного алгоритма «habrahabr.ru/post/267037», не более. Пришлось вспоминать школьный курс математики. Почему вы считаете предложенное решение неэффективным?

Keyten
30.09.2015 17:28Я придумал, давайте создадим массив пикселей, нарисуем там 2 прямые и поищем близко лежащие точки перебором всех пикселей.

Zenitchik
02.10.2015 15:46+1Сейчас буквально на коленке прикинул метод проверки наличия пересечения.
Если в уравнение прямой, подставить точку, то знак результата покажет нам, в какой полуплоскости находится эта точка относительно этой прямой.
Чтобы отрезки, не лежащие на одной прямой, пересекались, нужно, чтобы концы каждого из них находились в разных полуплоскостях относительно прямой, включающей другой отрезок.
Вычислительную сложность не прикидывал, но, думаю, при должной оптимизации должно получиться хорошо.
5nw
04.10.2015 06:28Да, это хороший способ. Но нужно еще учесть случай, когда точка конца одного отрезка будет лежать на прямой другого.
Если формализовать, то получим:
1. Даны два отрезка (x11, y11) — (x12, y12) и (x21, y21) — (x22, y22)
2. Проведем через эти отрезки прямые a1 * x + b1 * y + c1 = 0 и a2 * x + b2 * y + c2 = 0
3. Тогда отрезки пересекаются, если (a1 * x21 + b1 * y21 + c1) * (a1 * x22 + b1 * y22 + c1) <= 0 и
(a2 * x11 + b2 * y11 + c2) * (a2 * x12 + b2 * y12 + c2) <= 0
Все просто и логично
5nw
04.10.2015 06:40Провести прямую через отрезок (x1, y1) — (x2, y2) можно так
a = y2 — y1;
b = x1 — x2;
c = y1 * x2 — x1 * y2;


andy_p
Все эти алгоритмы страдают от неустойчивости решений, ввиду использования арифметики с плавающей точкой. Есть такой раздел науки — exact geometric computation, где рассматриваются подобные вопросы.