Публикуем вторую часть перевода материала об очень быстром алгоритме сортировки — «Ska Sort». В первой части говорилось о временной сложности алгоритмов и о том, какие улучшения базового алгоритма «Американский флаг» позволили автору «Ska Sort» повысить скорость сортировки. Сегодняшний материал посвящён рассказу о том, почему новый алгоритм быстрее других алгоритмов сортировки.

Прим. Wunder Fund: ну, вы наверное, и сами догадываетесь, как мы любим быстрые алгоритмы и оптимизации. Если вы тоже такое любите — вы знаете, что делать)
Почему новый алгоритм быстрее базового?
Новый алгоритм сразу же оказался намного быстрее, чем «Американский флаг». Это казалось мне совершенно ожидаемым, так как я думал, что мне удалось обойти проблему промахов кеша. Но как только я отпрофилировал код, я заметил, что в реализации этого алгоритма, на самом деле, случается даже немного больше промахов кеша. И тут, кроме того, имеется больше ошибочных предсказаний переходов. При работе кода ещё и выполняется больше инструкций. Но как-то так получается, что выполнение сортировки занимает меньше времени. Это выглядело довольно-таки загадочно, поэтому я принялся профилировать код всеми доступными мне способами. Например, я запускал его с помощью Valgrind для того чтобы узнать о том, что, по мнению этой системы, должно произойти с кодом. В Valgrind новый алгоритм оказался даже медленнее «Американского флага». В этом был смысл, так как Valgrind — это всего лишь симулятор. В результате в нём будет медленнее работать код, в котором выполняется больше инструкций, чем в другом; код, который вызывает больше промахов кеша и отличается немного увеличенным уровнем ошибочных предсказаний переходов. Но почему на реальном «железе» он работает быстрее?
Мне, прежде чем я всё понял, понадобилось больше суток вглядываться в результаты профилирования. Дело в том, что новый код отличается лучшим уровнем параллелизма на уровне команд. Тот, кто попробовал бы создать этот алгоритм и испытать его на старом компьютере, не увидел бы улучшения производительности. Большая проблема алгоритма «Американский флаг» заключается в том, что он ждёт окончания текущей операции обмена значений местами, прежде чем начать следующую такую операцию. И то, что там нет промахов кеша, ничего не значит. Современные процессоры могут одновременно обрабатывать несколько операций обмена значений местами в том случае, если им не нужно ждать окончания предыдущей подобной операции. Развёртывание внутреннего цикла тоже помогает обеспечить такую схему работы. Современные процессоры — это замечательные устройства. Получается, что они, на самом деле, способны выполнять несколько циклов параллельно даже без их развёртывания. Но если циклы развёрнуты — это идёт процессорам на пользу.
Linux-команда perf выдаёт одну метрику, которая называется instructions per cycle (количество команд, выполняемых за цикл). С помощью этого показателя оценивают состояние параллелизма на уровне команд. Реализация «Американского флага» на моём процессоре дала 1,61 команду за цикл. А у нового алгоритма этот показатель составил 2,24. Если за некий отрезок времени можешь выполнить на 40% больше команд, чем раньше, неважно то, что приходится выполнять немного большее количество команд для решения той же задачи.
А мои беспокойства по поводу промахов кеша и ошибок предсказания переходов оказались лишь мелочью, отвлекающей внимание. На самом деле, соответствующие показатели весьма невелики для обоих алгоритмов. В результате замеченный мной рост этих показателей был небольшим увеличением изначально весьма скромных чисел. Так как имеется лишь 256 возможных точек вставки, велики шансы того, что изрядная их доля всегда будет оказываться в кеше. А для многих видов реальных данных количество возможных точек вставки будет гораздо меньше. Например, при сортировке строк обычно этот показатель будет меньше 30, так как люди просто не пользуются намного большим количеством символов.
Учитывая вышесказанное, получается, что для маленьких коллекций «Американский флаг» оказывается быстрее. Высокий показатель параллелизма на уровне команд, похоже, даёт о себе знать лишь на коллекциях, размеры которых превышают тысячу элементов. В итоговой реализации моего алгоритма сначала анализируется количество элементов во входной коллекции. Если их меньше, чем 128, то я просто вызываю std::sort. Если их меньше 1024 — я вызываю реализацию «Американского флага». В противном случае я вызываю реализацию моего алгоритма.
Алгоритм std::sort представляет собой комбинацию алгоритмов, похожую на ту, которую использую я. Так, в нём смешаны алгоритмы быстрой сортировки, сортировки вставками и сортировки кучей. В результате и эти алгоритмы, в каком-то смысле, являются частью моего алгоритма. Если бы я как следует этим занялся, я мог бы создать такую входную последовательность, при сортировке которой использовались бы все эти алгоритмы. Такая последовательность представляла бы собой «самый худший случай» для моего алгоритма. А именно, это был бы худший случай алгоритма поразрядной сортировки, что заставило бы меня обратиться к std::sort. А потом оказалось бы, что это — худший случай для алгоритма быстрой сортировки, что заставило бы std::sort перейти к сортировке кучей. Поговорим о худших и лучших случаях для моего алгоритма.
Худший и лучший случай для моего алгоритма сортировки
Лучший случай моей реализации алгоритма поразрядной сортировки — это когда входные данные можно распределить по малому количеству разделов. Например, имеется тысяча элементов, и все они распределяются всего по трём разделам. Скажем — число 1 встречается 100 раз, число 2 — 400 раз, а число 3 — 500 раз. В таком случае на мой внешний цикл придётся совсем небольшая нагрузка, а внутренний цикл сможет переставлять элементы, помещая их на итоговые места, выполняя длительные непрерывные операции.
Ещё один лучший случай — это вызов реализации алгоритма для уже отсортированных последовательностей. В таком случае данные перебираются ровно два раза. Первый раз — чтобы взглянуть на каждый из элементов. Второй раз — чтобы поменять местами каждый элемент с самим собой.
Худший случай для моей реализации алгоритма достигается лишь при сортировке сущностей переменных размеров — вроде строк. Если речь идёт о ключах фиксированных размеров, вроде целых чисел, или чисел с плавающей точкой, то не думаю, что при таких ключах для моего алгоритма может существовать по-настоящему «плохой» случай. Один из подходов к конструированию последовательности, дающей худший случай алгоритма — это составить такую последовательность из строк вроде a, ab, abc, abcd, abcde, abcdef и так далее. Так как при поразрядной сортировке за один раз анализируется один байт, что позволяет выделить один элемент, это даст временную сложность алгоритма, равную O(n^2). Моя реализация алгоритма обнаруживает подобные ситуации, запоминая количество сделанных рекурсивных вызовов. Если их слишком много — делается переход на std::sort. В зависимости от конкретной реализации алгоритма быстрой сортировки, используемой в std::sort, это может быть и худшим случаем для быстрой сортировки.
Тогда std::sort перейдёт к алгоритму сортировки кучей. Я немного позанимался отладкой всего этого, и у меня создалось такое впечатление, что std::sort в моих тестах не доходит до сортировки кучей. Причина этого заключается в том, что в моих тестах использовались отсортированные данные, а std::sort, похоже, применяет для выбора опорного элемента метод, в соответствии с которым выбирается медиана из трёх элементов. В результате, если речь идёт об уже отсортированных последовательностях, выбираются удачные опорные точки. Зная это, пожалуй, можно создавать последовательности, которые приводят к худшим случаям и мой алгоритм, и алгоритм быстрой сортировки из std::sort, что приведёт к вызову реализации сортировки кучей. Но я не пытался составлять такие последовательности.
Не знаю о том, как часто это встречается в реальном мире, но из Boost-реализации алгоритма поразрядной сортировки я позаимствовал один приём, который заключается в том, что я пропускаю часто встречающиеся префиксы. Например, идёт сортировка записей лога, где имеется множество сообщений, начинающихся с warning или error. В моей реализации поразрядной сортировки подобные записи сначала будут выделены в отдельные разделы. А потом, в пределах каждого из этих разделов, система пропустит общий для всех записей префикс и продолжит сортировку записей с первого символа, которым они различаются. Этот приём должен способствовать тому, что мой алгоритм реже будет сталкиваться с худшим случаем.
Сейчас я обращаюсь к std::sort в том случае, если число рекурсивных вызовов в моём коде превышает 16. Я выбрал именно это число из-за того, что оно является первым числом, которое можно представить степенью 2, на котором не срабатывала моя система обнаружения худших случаев при сортировке кое-каких лог-файлов на моём компьютере.
Сводный обзор алгоритма и замечания о названиях
Я распространяю реализацию моего алгоритма сортировки «Ska Sort» в виде библиотеки. Не думаю, что часто буду изобретать новые алгоритмы сортировки, но если разработаю ещё какой-нибудь, может, использую в его названии не свою фамилию, а имя. Улучшенный алгоритм для сортировки байтов, который я описывал выше, в разделах «Оптимизация внутреннего цикла» и «Детали реализации» — это лишь небольшая часть моего алгоритма. А тот алгоритм называется «Ska Byte Sort».
Вот сводные данные по алгоритму Ska Sort:
Это — алгоритм поразрядной сортировки на месте.
За один раз сортируется один байт (используется 256 разделов).
Переходит на
std::sortв том случае, если входная коллекция содержит меньше определённого количества элементов (сейчас это пороговое значение — 128).Использует внутренний цикл алгоритма «Американский флаг» в том случае, если в состав коллекции входят элементы, количество которых меньше ещё одного порогового значения (сейчас это — 1024).
Если размер коллекции больше этого порогового значения — используется «Ska Byte Sort».
Рекурсивно вызывает себя для каждого из 256 разделов с использованием следующего байта в качестве ключа сортировки.
Переходит на
std::sortв том случае, если выполнено слишком много рекурсивных вызовов (сейчас — 16 вызовов).Использует
std::partitionдля сортировки логических значений.Автоматически преобразует целые числа со знаком, числа с плавающей точкой и символьные типы в корректные беззнаковые целочисленные значения.
Автоматически работает с парами чисел, кортежами, строками, векторами, массивами, сортируя за один раз один элемент.
Пропускает префиксы, часто встречающиеся в той или иной коллекции (например — при сортировке строк).
Поддерживает два механизма извлечения ключа сортировки из объектов. Это — объект функции, который может быть передан реализации алгоритма, или функция, называемая
to_radix_sort_key(), которую можно поместить в пространство имён пользовательского типа.
Как видите, Ska Sort — это сложный алгоритм. Он, определённо, сложнее, чем простой алгоритм быстрой сортировки. Одна из причин такой сложности заключается в том, что в реализации этого алгоритма широко используются сведения о типах сортируемых данных. В алгоритмах, основанных на сравнениях значений, имеется лишь функция для сравнения величин, возвращающая логическое значение. В случае же со Ska Sort мне, например, известно, что «работая с этой коллекцией я сначала выполню сортировку логических значений, а потом — чисел с плавающей точкой». Я могу написать код для обоих этих случаев. На самом деле, мне часто нужен особый код. Код, который сортирует кортежи, будет не таким, как код, который сортирует строки. Конечно, у них будет один и тот же внутренний цикл, но к этому циклу они приходят, выполняя различные действия. В сортировке же, основанной исключительно на сравнении величин, для сравнения данных любых типов используется один и тот же код.
Оптимизации, которые я не сделал
Если у вас, при чтении этой статьи, было достаточно времени на то, чтобы посмотреть материалы, ссылки на которые я давал, то вы могли заметить, что в этих материалах описаны две оптимизации, считающиеся важными, которыми я не воспользовался.
Первая, о которой речь идёт здесь, касается сортировки чисел с плавающей точкой. Заключается она в том, чтобы за раз обрабатывать значения длиной 11 битов, а не 1 байт. То есть — речь идёт о разбиении входной последовательности на 2048, а не на 256 разделов. Плюс такого подхода в том, что он позволяет сортировать четырёхбайтовые целые числа (или такие же числа с плавающей точкой) за три прохода вместо четырёх. Я попытался воспользоваться этим приёмом в прошлой публикации и обнаружил, что он даёт улучшение производительности лишь в редких случаях. В большинстве случаев это — медленнее, чем сортировка по одному байту. Вероятно, мне снова стоит попробовать этот приём, внедрить его в реализацию поразрядной сортировки на месте, но этого я не делал.
Вторая оптимизация — это та, которая обсуждается в этой публикации по алгоритму «Американский флаг». Она заключается в ручном управлении тем, за что у меня отвечает рекурсия. Вместо выполнения рекурсивных вызовов при таком подходе поддерживается стек, в котором содержатся сведения обо всех разделах, которые ещё надо отсортировать. Эти разделы обрабатывают до тех пор, пока стек не опустеет. Я не пытался прибегнуть к этой оптимизации, так как мой код и так уже слишком сложен. Эту оптимизацию легче внедрить в код в том случае, если этот код пишут исключительно для сортировки строк, так как для извлечения текущего байта используется всегда одна и та же функция. Но если можно сортировать целые числа, числа с плавающей точкой, кортежи, векторы, строки, и многое другое, то внедрение этой оптимизации усложняется.
Производительность
Вот мы и добрались до исследования скорости работы моего алгоритма. Я, с момента предыдущей публикации, изменил методику расчёта показателей производительности. В той публикации я, на самом деле, допустил большую ошибку. А именно, я измерял то, сколько времени занимает подготовка тестовых данных, а потом — сколько времени занимает их сортировка. Проблема тут в том, что на этап подготовки данных может уйти значительная доля времени. Поэтому в этот раз я отдельно измерял ещё и время подготовки данных и вычитал его из общего времени, что позволило узнать о том, сколько времени уходит на процедуру сортировки. Учитывая это — давайте проведём первое измерение: сортировку целых чисел (они сгенерированы с использованием std::uniform_int_distribution).

На графике показано время, необходимое для сортировки различных количеств элементов. Раньше я не говорил о ska_sort_copy. Это, по большей части, алгоритм из моей предыдущей публикации. В него я внёс изменение, в соответствии с которым он, если нужно, переходит на ska_sort, а не на std::sort (но, конечно, ska_sort способен принять решение о переходе на std::sort).
Одна из проблем этого графика заключается в том, что, глядя на него, очень трудно разобраться с тем, что именно на нём происходит (и это — несмотря на то, что я воспользовался логарифмической шкалой). В прошлый раз я добавлял в нижней части графика линию, показывающую относительный масштаб, но в этот раз у меня есть кое-что получше. Вместо использования логарифмической шкалы я могу поделить общее время на число элементов. В результате получится время, которое реализация алгоритма тратит на сортировку одного элемента.
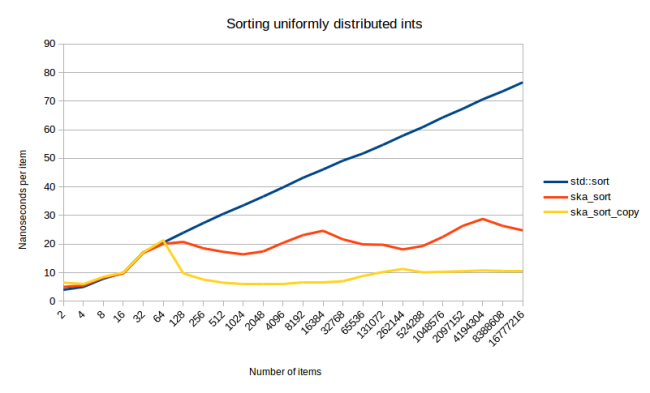
Теперь нам гораздо легче разобраться с тем, что тут происходит. Все следующие графики построены по тому же принципу, что и этот график, с использованием осей «Наносекунд на элемент» и «Количество элементов». Проанализируем этого график.
Сортировка нескольких первых групп элементов демонстрирует практически полную схожесть трёх рассматриваемых алгоритмов. Если во входной коллекции меньше 128 элементов, мой алгоритм автоматически переходит на std::sort. Поэтому тут можно ожидать, что линии всех трёх графиков должны полностью совпадать. Их отличия — это влияние погрешностей измерений.
Потом мы видим, что std::sort — это алгоритм, временная сложность которого составляет в точности O(n log n). Его график, демонстрирующий результат деления времени на количество элементов, линейно возрастает, а это именно то, чего можно ожидать от O(n log n). На самом деле — впечатляюще выглядит то, как график вытягивается в прямую линию после прохождения групп, содержащих небольшое число элементов. Ska_sort_copy — это настоящий алгоритм сортировки с временной сложностью O(n). Затраты времени на сортировку одного элемента остаются постоянными при увеличении количества элементов. А ska_sort… этот алгоритм — он сложнее других.
Волны, которые видны на линии ska_sort, связаны с количеством рекурсивных вызовов. Алгоритм ska_sort работает быстрее всего на больших количествах элементов. Именно поэтому линия сначала идёт вниз. Но потом в какой-то момент получается так, что нам нужно рекурсивно обрабатывать множество разделов, размер которых лишь немного превышает 128 элементов. А это уже медленно. Затем, по мере роста количества элементов, растёт и размер этих разделов, и алгоритм снова ускоряется, до тех пор, пока мы не доходим до момента, когда размеры разделов снова превышают 128 элементов, и нам нужно добавить новый шаг рекурсии. Один из способов визуализации этого процесса заключается в построении графика сортировки коллекции значений типа int8_t.
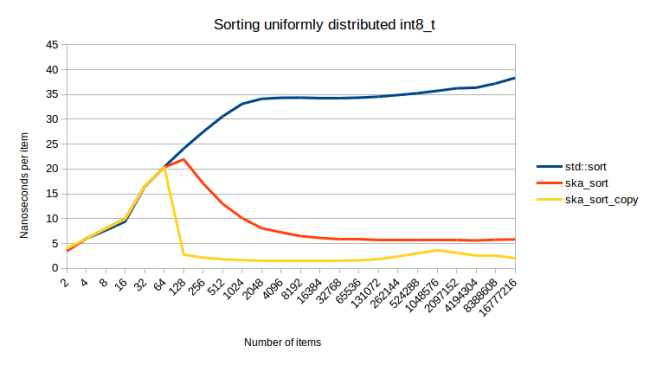
Как видите, в начале затраты времени на один элемент сильно уходят вниз. Именно потому, что алгоритму периодически нужно рекурсивно обрабатывать другие разделы, график сортировки целых чисел и получился волнообразным. Это видно там, где начальные части линий накладываются друг на друга.
Выше я говорил о том, что ska_sort работает быстрее всего в том случае, если количество разделов, содержимое которых нужно отсортировать, невелико. Посмотрим, что произойдёт, когда я, вместо std::uniform_int_distribution, воспользуюсь для генерирования набора чисел std::geometric_distribution.
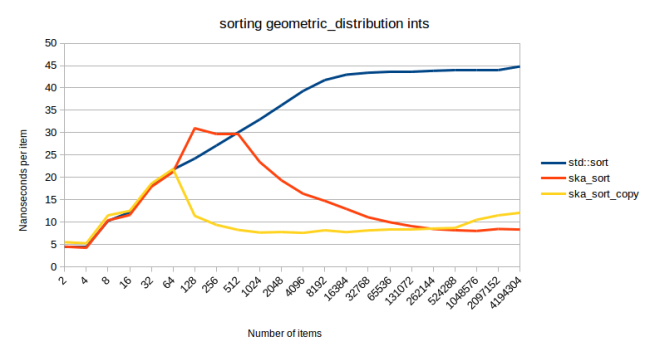
Этот график, снова, демонстрирует сортировку четырёхбайтовых целых чисел. Поэтому можно ожидать, что тут будут видны те же «волны», которые мы видели на графике сортировки равномерно распределённых целых чисел. Я использовал std::geometric_distribution со значением 0.001 в роли аргумента конструктора. Это значит, что получаются числа от 0 до примерно 18000, но большинство чисел будет близко к 0. (В теории могут быть сгенерированы и числа, которые гораздо больше 18000, но самым большим встретившимся мне числом было 18882). А, так как большая часть чисел близка к нулю, будет выполнено меньше рекурсивных вызовов, из-за чего на графике меньше волн, что делает мой алгоритм во много раз быстрее, чем std::sort.
Между прочим, подскок графика ska_sort, произошедший в самом начале, стал для меня неожиданностью. На всех остальных данных, которые мне удалось найти, ska_sort обходит std::sort на последовательностях, размер которых начинается со 128 элементов. А тут всё выглядит так, будто ska_sort становится быстрее std::sort немного позже. Причина такого поведения алгоритма мне неизвестна. Может, я ещё с этим разберусь, но мне не хотелось бы менять уже выбранное пороговое значение, так как оно хорошо показывает себя для всех остальных значений. Изменение порогового значения немного сдвинет все остальные линии вверх. Кроме того, так как мы сортируем тут небольшое количество элементов, в абсолютном выражении разница не слишком велика — от 15,8 до 16,7 микросекунд для 128 элементов, и от 32,3 до 32,9 микросекунд для 256 элементов.
Посмотрим на другие варианты применения алгоритма. Вот — мой «пример из реального мира», о котором я говорил в предыдущей публикации, где мне нужно было сортировать врагов в игре по их расстоянию к персонажу игрока. Мне было нужно, чтобы все враги, участвующие в битве, шли первыми, отсортированные по расстоянию, и чтобы за ними шли все враги, которые в настоящий момент не сражаются, тоже отсортированные по расстоянию. Это сводится к сортировке пар значений (std::pair).

График получился, в целом, таким же, как при сортировке целых чисел, но все линии немного сдвинуты вверх. Этого, полагаю, и следовало ожидать. Но отрадно видеть то, что конверсия, которую мне приходится делать для чисел с плавающей точкой, и разделение, которое надо выполнять для пар значений, не добавили значительной дополнительной нагрузки на систему. Более интересный график получился при анализе сортировки значений типа int64.
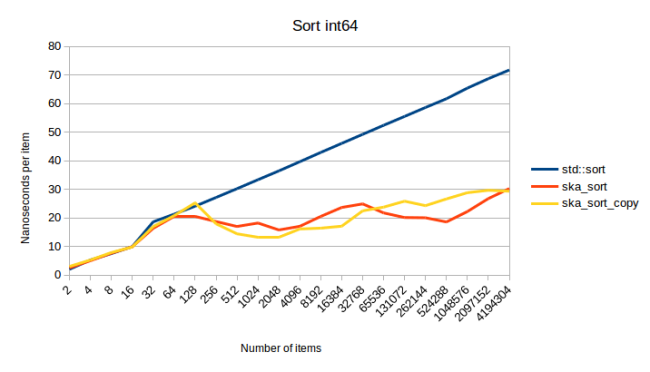
В этом эксперименте ska_sort_copy иногда оказывается медленнее, чем ska_sort. Я, на самом деле, решил снизить пороговое значение, при котором ska_sort_copy переходит на ska_sort. А именно, теперь алгоритм обходится своими силами, выполняя поразрядную сортировку с копированием, лишь до тех пор, пока ему нужно выполнить менее восьми проходов по входным данным. То есть, я изменил код, в результате ska_sort_copy для значений типа int64, на самом деле, просто вызывает ska_sort. Основываясь на предыдущем графике, можно сказать, что алгоритм ska_sort_copy должен продолжать использовать поразрядную сортировку с копированием. Но вот — измерения для сортировки 128-байтной структуры с использованием, в качестве ключа сортировки, значения типа int64.
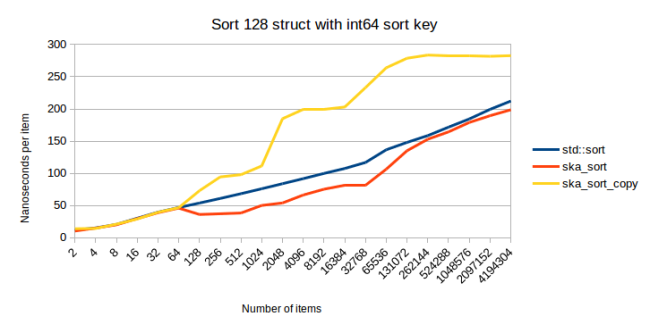
По мере роста количества структур ska_sort_copy замедляется. Из-за этого я и решил переводить ska_sort_copy на ska_sort для сортировки ключей такого размера.
На предыдущем графике можно заметить то, что линии ska_sort и std::sort сближаются. Значит ли это, что ska_sort может стать медленнее std::sort? Полагаю — не значит. Вот что происходит при сортировке структуры размером 1024 байта.
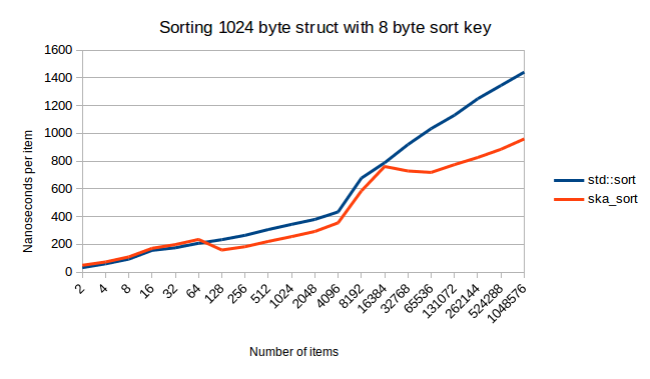
И, опять, перед нами очень интересный график. Хотел бы я иметь возможность и время исследовать причины появления столь большого разрыва между линиями в правой части графика. Это — не погрешность измерений. Этот результат воспроизводим. Я построил этот график, тридцать раз запустив Google Benchmark, сделав так, чтобы снизить шансы случайных вариаций результатов.
Если говорить о больших объёмах данных, то, в прошлой моей публикации, худшим случаем алгоритма была сортировка структуры с 256-байтным ключом сортировки. В данном случае это означает использование в качестве ключа сортировки std::array. В результате поразрядная сортировка с копированием работала очень медленно, так как тут приходится делать 256 проходов по данным. При поразрядной сортировке на месте достаточно проанализировать достаточно байтов, после чего система сможет различить два фрагмента данных, поэтому такая сортировка может быть быстрее. И, если судить по результатам измерений, похоже, так оно и есть.
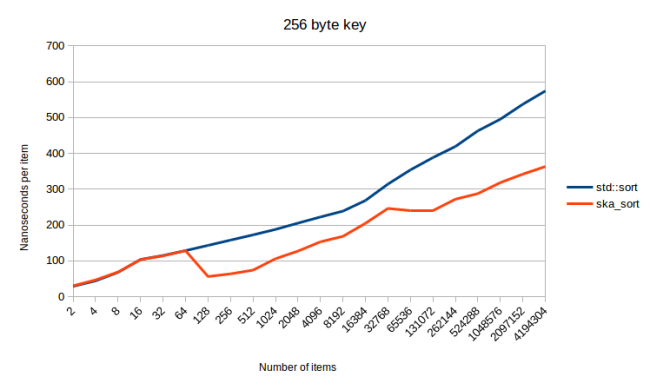
Алгоритм ska_sort_copy при обработке подобных данных перейдёт на ska_sort, поэтому график ska_sort_copy будет точно таким же, как график ska_sort. Получается, что тут я справился с худшим случаем из предыдущей публикации. Но, когда я готовил ту публикацию, я не мог профилировать мой код при сортировке строк. Дело в том, что алгоритм ska_sort_copy просто не может сортировать строки, так как он не может работать с элементами переменной длины.
Посмотрим на то, как ska_sort сортирует строки.
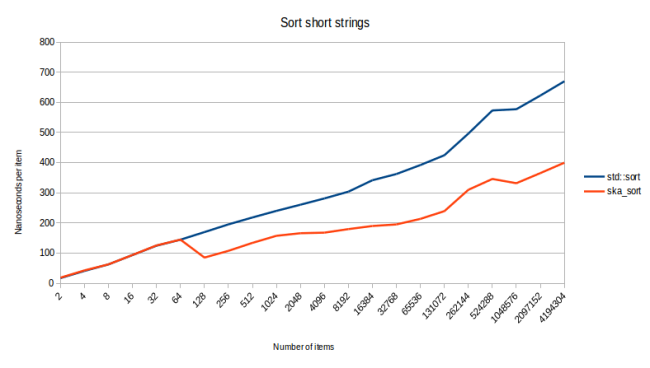
Данные для этого испытания я подготовил, выбирая от одного до трёх случайных слов из моего файла words и конкатенируя их. Я, опять же, очень рад видеть успех моего алгоритма. Правда, этого и следовало ожидать. Давно известно, что поразрядная сортировка отлично подходит для работы со строками.
Но сортировка строк — это задача, на которой мой алгоритм может наткнуться на свой худший случай. В теории — можно столкнуться с такими входными данными, по которым нужно делать множество проходов, так как конкретные значения представлены множествами байтов, многие из которых совпадают друг с другом. Я попытался узнать о том, что произойдёт, если попробовать отсортировать строки разной длины, конкатенируя от 0 до 10 слов из файла words.
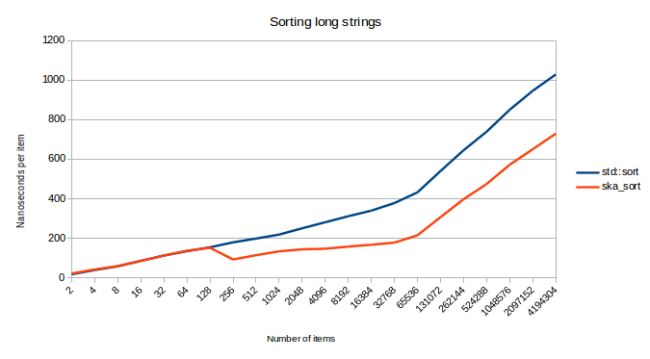
При сортировке миллионов длинных строк, похоже, ska_sort ведёт себя как алгоритм с временной сложностью O(n log n). Но ska_sort при этом не становится медленнее std::sort. Лучшее объяснение, которое я могу дать тому, что кривая графика в конце уходит вверх, заключается в том, что ska_sort приходится, при обработке этих данных, делать много рекурсивных вызовов. Причём — этих вызовов не достаточно для того, чтобы сработала бы моя система обнаружения худшего случая, но и эти вызовы ощутимо влияют на производительность, так как они требуют выполнения дополнительного прохода по данным.
Я попробовал снизить пороговое значение, связанное с рекурсией, до восьми. В данном случае обнаружение худшего случая срабатывает на миллионе элементов. Но и в этом случае график выглядит, в целом, таким же, как раньше. Причина происходящего в том, что это было ложноположительное срабатывание, и данные не довели алгоритм до настоящего худшего случая. Алгоритм сортировки при этом преуспел в разбиении данных на множество небольших разделов. Поэтому, когда был осуществлён переход к std::sort, работать ему было гораздо легче, чем тогда, когда ему нужно было бы сортировать всю последовательность.
И наконец — вот что происходит, когда я сортирую контейнеры, которые устроены несколько сложнее, чем строки.
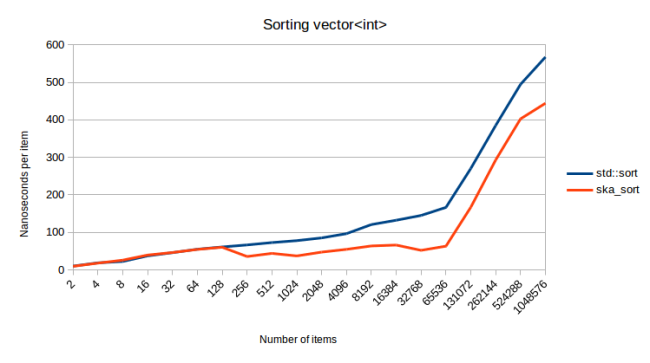
Для этого эксперимента я сгенерировал векторы, содержащие от 0 до 20 целых чисел. Получается, что я сортирую векторы векторов. Резкий скачок линии графика в конце выглядит очень интересно. Здесь не срабатывала моя система, реагирующая на слишком большое количество рекурсивных вызовов, поэтому я не знаю точно того, почему сортировка вдруг стала требовать гораздо больше ресурсов, чем раньше. Возможно, мой процессор просто не любит работать с такими большими объёмами данных. Но я с удовольствием сообщаю о том, что ska_sort в течение всего этого эксперимента, как и в других рассмотренных случаях, быстрее std::sort.
Так как возникает такое ощущение, что ska_sort всегда быстрее std::sort, я сгенерировал входные данные, рассчитанные на достижение алгоритмом ska_sort худшего случая. На следующем графике показано, что это происходит сразу же по достижении размера последовательности в 128 элементов. Но ska_sort эту ситуацию распознаёт и переходит на std::sort.

Тут я сортирую случайную комбинацию векторов {}, { 0 }, { 0, 1 }, { 0, 1, 2 }, … { 0, 1, 2, … , 126, 127 }. Так как каждый элемент сообщает моему алгоритму лишь о том, как разделить 1/128 часть входных данных, мне понадобилось бы 128 раз прибегать к рекурсии. Но на шестнадцатом рекурсивном вызове ska_sort сдаётся и прибегает к помощи std::sort. На вышеприведённом графике можно видеть то, как много дополнительной нагрузки на систему это создаёт. И эта нагрузка больше, чем мне хотелось бы, особенно — для больших коллекций. А вот на маленьких наборах данных она, похоже, не так уж велика. Мне не нравится то, что эта дополнительная нагрузка вообще существует, но меня полностью устраивает то, что ska_sort обнаруживает худший случай, и, как минимум, не скатывается к временной сложности O(n^2).
Продолжение следует…
О, а приходите к нам работать? ????
Мы в wunderfund.io занимаемся высокочастотной алготорговлей с 2014 года. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.
Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.
Сейчас мы ищем плюсовиков, питонистов, дата-инженеров и мл-рисерчеров.
Комментарии (3)

AndrewB330
28.12.2021 20:34+1Сравнивать std::sort с алгоритмом сортировки подсчётом? Это можно сделать чтобы похвастаться во дворе, но не более. Это разные классы алгоритмов, одни работают на любых данных, другие - на определенных данных, но быстрее
P.S. вижу что в комментах к оригинальной статье на это тоже указывали


nickolaym
В первой части вам уже задали вопрос: https://habr.com/ru/company/wunderfund/blog/597113/#comment_23855877
Зачем публиковать тремя частями то, что уже до вас перевели целиком?
Выглядит, как кликбейт. Привлечь внимание не к статье, а к вашей конторе.
mr-pickles Автор
Мы видели тот комментарий — да, два перевода в один день выглядят действительно необычно. Однако не хотелось бы, чтобы кто-то из читателей думал, что кто-то у кого-то списал — если сравнить статьи, видно, что они разные.
Так получилось, что к тому моменту мы уже перевели статью, но не решились почти 60 килобайт текста размещать одним большим постом. Поэтому решили выпустить его несколькими частями — вовсе не из-за погони за рейтингом (за переводы его почти не начисляют).
А то, что материал набрал высокий рейтинг (и у нашей статьи и у той) говорит лишь о том, что информация полезна и востребована, поэтому мы всё же решили её доразместить согласно нашему графику выпуска постов (1 в неделю). Рассчитываем на понимание :)