Как вам преподавали квадратные уравнения в школе? Это был 7-8 класс, примерно. Вероятнее всего, вам рассказали что есть формулы корней через дискриминант, что направление ветвей зависит от старшего коэффициента. Через пару занятий дали теорему Виета. Счастливчикам еще рассказали про метод переброски. И на этом решили отпустить.
Вы довольны такой базой? Вам не рассказали ни геометрический смысл, ни как это получить.
Спустя некоторое время обдумывания сей несправедливости, я решил написать эту статью и тем самым закрыть гештальт о фрагментарности знаний.
Вы не найдете здесь ничего нового по факту, но, возможно, это даст посмотреть на такое простое понятие с другой стороны.
Начнем с конца
Когда я перечислял темы, касающиеся квадратных уравнений, я делал это примерно в том же порядке, в котором изучают их в школе. Но такой порядок не оправдан с точки зрения обучения, и вот почему:
Дискриминант дается просто как данность (за редким исключением, когда показывают вывод этих формул через приведение к полному квадрату)
Мощнейшая по своей сути теорема Виета дается в конце и только как эвристический способ решения
Гораздо проще начать с теоремы Виета.
Рассмотрим квадратный трехчлен
В силу основной теоремы алгебры (примем её как данность, так как её действительно тяжело доказать), мы знаем, что у этого уравнения должно быть два корня. Допустим, что это некоторые числа . Тогда можно переписать изначальное уравнение как выражение его корней:
Оба эти уравнения эквиваленты, так как они оба зануляются в (первое по определению
, второе по построению).
Раскрывая скобки, мы получим следующее:
Откуда приравняв соответствующие коэффициенты с имеющимися, получим знаменитую систему:
Мы только что доказали теорему Виета на случай квадратного трехчлена. Это потрясающий результат: мы начинаем получать некоторую информацию о корнях, которые, как мы предположили, существуют. И этот результат мы будем использовать далее.
Геометрия параболы
Вершина
Здесь можно было бы рассказать весь первый курс алгебры университета: о фокусах, директрисах, о конических сечениях, первой и второй производной…
Но раз мы ограничились школьной программой (7-8 класс, если быть точным), то и рассуждения у нас будут простые.
Самая, на мой субъективный взгляд, интересная точка параболы – это её вершина. Она уникальным образом задает положение параболе и дает понимание о том, как устроены корни.
Но формулу для нее мы не знаем, до первых понятий о производной нам еще 3 года в среднем. Будем выкручиваться.
Парабола – симметричная фигура. До того момента, как мы сдвинули ее относительно оси , ось
служит для нее осью симметрии. Когда же мы начинаем ее сдвигать, становится видно, что она продолжает быть симметричной, но уже относительно оси, проходящей через вершину.

Тогда от вершины в обе стороны до корней равные расстояния, а это значит, что вершина параболы лежит ровно между корнями. Тогда координата вершины это среднее между ее корнями
Пока что мы не знаем наши корни. Но благодаря теореме Виета мы знаем, чему равна сумма корней!
Потрясающий результат, который нам пригодится далее.
Ещё немного про корни
Мы знаем, что корни, графически, это те точки, в которых кривая пересекает ось . Очень полезное знание, учитывая, что смотря на параболу, исключительно визуально, мы понимаем что у нас может быть 3 случая:
-
Корней нет, при этом
Либо значение в вершине больше нуля и старший коэффициент больше нуля
Либо значение в вершине меньше нуля и старший коэффициент меньше нуля
Корень один, но кратности 2 (не забываем основную теорему алгебры), и значение в вершине равно нулю
Корня два
Второй случай тривиален, до третьего мы еще дойдем. Интересно математически взглянуть на первый. Найдем значение квадратного трехчлена в вершине:
И теперь все же рассмотрим первый случай: парабола висит над осью ветвями вверх.

Домножим первое неравенство на . Учитывая, что
, знак неравенства сменится на противоположный:
Это условие, при котором корней нет.
Рассмотрим вкратце противоположный случай: парабола висит под осью ветвями вниз.

Какая-то магия. Получается, что это условие инвариантно относительно положения параболы. Но тем оно лучше.
На данном этапе прошу заметить, что это только условие отсутствия действительных корней. Да, это похоже на дискриминант, но давайте представим, что вы этого не знаете.
Понятие дискриминанта
Мы уже многое поняли о корнях: в какой они связи с коэффициентами, когда они не существуют, каким образом они лежат относительно вершины. Все это безумно полезно, но это все до сих пор не способ найти значения алгебраически.
Давайте будем отталкиваться от того, что мы уже знаем: от вершины. Если бы мы каким-то образом знали расстояние между корнями, то могли бы однозначно найти и сами корни.
Таки что мешает нам это сделать? Но как настоящие математики, давайте находить квадрат расстояния между корнями. Не теряя общности, будем считать, что – больший корень. Тогда
Пока что выглядит не очень, но на что-то это очень сильно похоже. Не видите? Давайте выделим полный квадрат, но по сумме, а не по разности: добавим , но чтобы все осталось в точности так же, это же и вычтем.
Все еще не видите? Воспользуемся снова теоремой Виета:
Мы получили квадрат расстояния между корнями с учетом растяжения коэффициентом .
Так мы теперь можем найти корни! Вершина параболы да половину расстояния между корнями в обе стороны:
Или, немного преобразовав
Квадрат расстояния между корнями квадратного трехчлена и есть дискриминант.
В общем случае, дискриминант - более сложное понятие, связанное с кратными корнями. Но для квадратного уравнения в 7 классе этого достаточно.
Теперь, если рассуждать о дискриминанте как о расстоянии, становится логично и понятно, почему если он равен нулю, то корень всего один; а если отрицательный, то действительных корней вообще нет.
Заключение
Заметьте, что единственное, что мы предположили, что корня два и они существуют. Единственное, что приняли на веру, это основную теорему алгебры. До всего остального мы дошли исключительно умозрительными заключениями и простейшей алгеброй.
Как по мне, это именно то, как должны преподавать эту тему в школе.
Комментарии (74)

nerudo
10.03.2022 16:45+2Втолковывая младшекласнику бездарно изложенные премудрости математики, я задумался — а должен ведь быть какой-нибудь учебник/монография/незнаючто, где базовая математика излагалась бы компактно, здравым языком и для взрослых, а не как обычно. Может кто посоветует?

Joysi
11.03.2022 09:29Мне понравились цикл видеолекций Савватеева (правда для учеников старших классов — www.youtube.com/watch?v=Nd5VJAR3ZPw&list=PLmu_y3-DV2_k-Tnu_L-uZ8FMbTWGce-ED) о выводе экспоненты, где пляшут от природы экспоненты. У него есть курсы и для младших классов.

Fell-x27
10.03.2022 17:00+19Это вот основная причина, почему я не любил математику в школе, хоть и получал по ней пятерки. Тебя просто заставляют учить какие-то эльфийские заклинания и ритуалы, не объясняя, зачем это, как это работает, что это значит, а какого черта вообще происходит.
До какого-то момента смысл математических операций объясняют. Сложение\вычитание\умножение\деление через распределение апельсинов в группе детей. Отрицательные числа через понятие денег и долгов. Но потом, в какой-то момент просто начинается "нет времени объяснять, зубрите формулу" и темнота... Максимально контрпродуктивно. Такое ощущение, что учителя уже и сами не знают, что и как в энтой вашенской математике работает. Просто какие-то умные люди от скуки напридумали кучу бесполезных формул, чтобы усложнить всем жизнь.
P.S. Из старших классов еще помню, молодая практикантка объясняла нам смысл интеграла. Мб по той причине, что сама еще помнила его, в отличие от "опытных учителей".
P.P.S. Сейчас работаю с криптографией, эллиптическими кривыми, разномастными преобразованиями, производными и учил все это уже сам сильно после университета, где алгебра линейная подавалась еще топорнее, чем в школе.

edo1h
11.03.2022 05:21+9Тебя просто заставляют учить какие-то эльфийские заклинания и ритуалы,
странно, я любил (и люблю) школьную математику как раз по обратной причине: почти ничего не нужно учить, нужно понять.
забыл дискриминант — вывести недолго, забыл синус двойного угла — вывести недолго (вот прямо сейчас ради проверки сел и вывел, школу закончил 30 лет назад), забыл точную формулировку теоремы — можно переформулировать.с историей или даже с химией так не выйдет.
не объясняя, зачем это, как это работает, что это значит, а какого черта вообще происходит.
а что значит «зачем»? just for fun же )
существенная часть математики была придумана из «хм, прикольная штука, а как её можно покрутить?», важный частный случай этого «покрутить», о котором я уже писал: «ну да, это сделать нельзя, а давайте представим, что можно, что тогда получится?» (отрицательные числа появились из попытки отбросить правило «из меньшего нельзя вычесть большее», дробные числа из «число нельзя разделить на другое число, не являющееся его делителем», комплексные из «из отрицательного числа нельзя извлечь корень»).
а «зачем» уже после находилось.
Refridgerator
11.03.2022 06:17забыл синус двойного угла — вывести недолго (вот прямо сейчас ради проверки сел и вывел, школу закончил 30 лет назад)
А синус, например, 17-кратного угла сможете вывести?
Alexandroppolus
11.03.2022 06:29Достаточно промыслить sin(a+b), а остальное дело техники

Refridgerator
11.03.2022 06:39Недостаточно.

edo1h
11.03.2022 06:56+2геометрически, как я выводил синус двойного угла/суммы? не буду браться.
тригонометрически через синус/косинус суммы? чисто механическая работа, дело лишь в аккуратности.только я не понял к чему вы привели пример, эту формулу от школьников не требуют.
я пытался сказать вот что:
если на контрольной забыл формулу/теорему, не беда, вседа можно вывести, пользовался этим неоднократно.
то же самое если вызвали сформулировать/доказать теорему, если помнишь про что она, то не нужно помнить точную формулировку, можно строго сформировать на ходу; ну а если разбирал доказательство, то через несколько минут вспоминаешь идею и можешь повторить (хотя было, что в голову приходило альтернативное доказательство).другими словами, школьный курс математики для меня представлял полную противоположность зубрёжке.
ну да, надо запомнить, что «биссектриса — это такая крыса, которая бегает по углам и делит угол пополам» (честно запомнил что такое биссектриса до того, как встретил этот стишок), и что синус — отношение противолежащего катета к гипотенузе (тут запоминал как казус — основной синус дальше от угла, а прилегает к углу парный ко-синус), но в сравнении с остальными предметами это мелочи.
ZetZet Автор
11.03.2022 07:35На самом деле, это правильная мысль: запоминать не факты, а идеи. Еще лучше получается тогда, когда эти идеи начинают связываться друг с другом.

Refridgerator
11.03.2022 07:39+1Я этот пример привёл к тому, что школьные знания остаются на школьном же уровне. Выводить синус n-кратного угла через синус/косинус суммы — это то же самое, что и умножать числа последовательным сложением — довольно непродуктивно. Для небольших n в пределах 10 — да, можно. Но стоит увеличить n на несколько порядков — и у вас уже жизни не хватит на «чисто механическую работу».
Решение для n=17sin(17·x) = 17·sin(x)-816·sin3(x)+11424·sin5(x)-71808·sin7(x)+239360·sin9(x)-452608·sin11(x)+487424·sin13(x)-278528·sin15(x)+65536·sin17(x)
Форматирование этого равенства заняло у меня намного больше времени, чем собственно его нахождение. Через комплексные числа, которые тоже изучают в школе, универсальное решение будет ещё более компактным — но могу поспорить, что далеко не каждый знаток корня из минус единицы сможет его предоставить.
Andy_U
11.03.2022 11:06Вот не лень же было? Я Maple запустил:
expand(subs(seq(cos(x)^(2*n)=cs2^n,n=1..8),cs2=1-sin(x)^2,expand(sin(17*x))));
Refridgerator
11.03.2022 11:54В смысле «не лень»? У вас более громоздкое решение, к тому же годится только для целых n. Имея на руках калькулятор или язык программирования без поддержки символьной алгебры от него мало толку. Особенно учитывая то, что при n>50 коэффициенты при синусе становятся настолько большими, что перестают влазить в 16 цифр, то есть предельную точность double.

Andy_U
11.03.2022 12:36У вас более громоздкое решение
Oтвет ровно такой же, как и у вас. Только maple (2020.1) не сортирует члены выражения:
-816*sin(x)^3 + 11424*sin(x)^5 - 71808*sin(x)^7 + 239360*sin(x)^9 - 452608*sin(x)^11 + 487424*sin(x)^13 - 278528*sin(x)^15 + 65536*sin(x)^17 + 17*sin(x)к тому же годится только для целых n
А вы, значит, можете превратить sin(17.12345x) в полином по степеням sin(x)?
Имея на руках калькулятор или язык программирования без поддержки символьной алгебры от него мало толку. Особенно учитывая то, что при n>50 коэффициенты при синусе становятся настолько большими, что перестают влазить в 16 цифр, то есть предельную точность double.
Спасибо, а то я не догадывался. Я думаю, что уже при N=17 будет потеря точности. Я просто удивился, что кто-то решил ручками такие технически элементарные операции сделать. Я бы точно ошибся где-нибудь.

Refridgerator
11.03.2022 13:02Oтвет ровно такой же, как и у вас
Само собой. Я говорил об изначальной постановке задачи, для которой существует не итеративное решение, а в замкнутом виде через многочлены Чебышева.А вы, значит, можете превратить sin(17.12345x) в полином по степеням sin(x)?
Да, только он будет бесконечным:
17.12345·sin(x)-
833.9478027322436·sin(x)^3+
11850.921158031997·sin(x)^5-
75680.13485666757·sin(x)^7+
256694.97157653485·sin(x)^9-…
Andy_U
11.03.2022 13:19Ну, полиномы Чебышева формально итеративно определены...
Только это ряд, а не полином, вдобавок, как бы еще не расходящийся?

Refridgerator
11.03.2022 13:54Ну, полиномы Чебышева формально итеративно определены...
Итеративное определение — это одно из возможных определений, а вовсе не единственно верное, и уж тем более не очевидно полученное из поставленной задачи (минимизация отклонений). Один из вариантов вообще определяет многочлены Чебышева как частный случай многочленов Золотарёва, а те, в свою очередь, определяются через эллиптические (и трансцендентные) функции.Только это ряд, а не полином
Будет интересным узнать, чем отличается многочлен от степенного ряда с конечным количеством членов.как бы еще не расходящийся?
Не расходящийся. А расхождение ряда не значит, что его сумму нельзя посчитать — примеры вы и без меня знаете.

Andy_U
11.03.2022 14:00Да, только он будет бесконечным: 17.12345·sin(x)- 833.9478027322436·sin(x)^3+ 11850.921158031997·sin(x)^5- 75680.13485666757·sin(x)^7+ 256694.97157653485·sin(x)^9-…
Я вот про этот ряд писал....

Refridgerator
11.03.2022 14:08Я понял. Его вполне легально можно ограничить до конечного, если ограничить необходимую точность вычислений. Особенно учитывая то, что в численных вычислениях точность входных данных тоже ограничена.

Refridgerator
11.03.2022 20:06Дальше они вниз пойдут, не переживайте. Коэффициенты ряда вовсе не обязаны монотонно затухать или возрастать — они могут иметь и колоколообразный вид, разложите для примера бином Ньютона.

Andy_U
11.03.2022 12:39Вдогонку, а если N=16? :)

Refridgerator
11.03.2022 13:16Косинус придётся привлечь (но его можно через квадратный корень посчитать):
Cos(x)·(16·Sin(x)-672·Sin(x)^3+
8064·Sin(x)^5-42240·Sin(x)^7+
112640·Sin(x)^9-159744·Sin(x)^11+
114688·Sin(x)^13-32768·Sin(x)^15)
Но лучше, конечно, сразу к комплексным числам перейти — там это будет просто возведением в степень, хоть целую, хоть дробную, хоть мнимую.

edo1h
11.03.2022 12:15Я этот пример привёл к тому, что школьные знания остаются на школьном же уровне
напомню, изначально дискуссия была про то является ли школьная математика зубрёжкой или нет.
я сказал что нет.
в качестве аргумента я взял листочек, карандаш и минут за 10 вывел геометрически синус двойного угла. в школьные годы я бы, разумеется, сделал это быстрее, ибо планиметрии и тригонометрии все эти десятилетия после школы не касался, максимум несколько раз решал попадавшиеся задачки.так вот, речь была про то, что если не помнишь формулу, то не надо зубрить, надо понять как она выводится — и оказывается вполне реально вывести её прямо на контрольной (что я неоднократно в школьное время и делал).
для сравнения, вывести дату бородинской битвы вряд ли получится, её можно только запомнить.
что должен был означать ваш пример в контексте этой беседы я так и не понял.

Refridgerator
11.03.2022 12:38Перефразирую: повторить процедуру вывода синуса двойного угла, опираясь на тригонометрические тождества — это одно, доработать её для произвольного случая, пригодного для численных вычислений — уже несколько другое. Математическое мышление предполагает не только умение использовать готовые решения, но и находить новые. В школе, как правило, этому не учат, а сама школьная программа отстаёт лет на 100 (впрочем, и этого многим не нужно).

Wesha
11.03.2022 07:49честно запомнил что такое биссектриса
Чего тут запоминать? "Би" - "два" (см. "биплан"), и "сек/сечь". То есть "секу надвое".

mikleh
10.03.2022 19:26+8До всего остального мы дошли исключительно умозрительными заключениями и простейшей алгеброй.
А вот меня, когда я учился, всегда бесила эта отвратительная особенность школьной программы, когда там какими-то обезьяньими ужимками пытаются доказывать вещи, для доказательства которых давным давно придумали удобнейший аппарат, а сам этот аппарат дают позднее. Типа как в начале 9 класса проходят механику на физике, но при этом производные будут только в конце 9 класса и у физика есть выбор:
1) взять бубен и какими-то маловразумительными построениями объяснить что такое ускорение (как это и предполагалось многомудрыми методистами МО)
2) забить болт (что в средней школе условного Урюпинска и будет сделано — без сомнения)
3) сказать что ускорение — это производная скорости по времени и быстренько объяснить детям, что такое производная, вместо математика (ну это если учитель реально крут)
Ну почему же по порядку нельзя все объяснить? Что, дети в 6ом классе не поймут что такое синус? Нет надо им в 9ом объяснять бред про отношение противолежащих к прилежащим, а потом уже в институте немногие прошареные осознают, что это всего-навсего ордината точки на единичной окружности. А по хорошему это надо было всем еще в 6ом сказать.
Vsevo10d
10.03.2022 22:55+5Я с вами полностью согласен.
Но обратная сторона - все это имеет смысл только при дальнейшей специализации.
Например, абсолютно тупо преподавать химию, особенно органическую, без объяснения квантовых основ строения атома: квантовых чисел, правил Хунда, Клечковского, понятия об атомных и молекулярных орбиталях, гибридизации и вырождения. То же стоит сказать про химическую кинетику. Это все можно рассказать в доступной форме, на схемах и графиках, зато потом не будет отношения к химическим реакциям как к арифметике со странными законами, ошибок про пятивалентный атом углерода и костылей вроде правила Вант-Гоффа или закона действующих масс.
А это приводит нас к более фундаментальной дилемме: а) с одной стороны, людям, которые не собираются в дальнейшем изучать химию/биологию, такая детализация не нужна (хотя и безусловно полезна в формировании правильных основ дисциплины, без костылей и "забудьте все, чему вас учили в школе" в универе), с другой - вообще является полным бредом специализировать ученика в 7-8 классе. Я вон даже универ закончил не по той специальности, чем занимаюсь сейчас.

Pavel1114
11.03.2022 05:04+1Вообще разделение физики и математики в школе, на начальном этапе изучения, мне кажется неправильным. Тоже самое про географию, историю, основы экономики — очень многое становится понятнее, если изучать эти предметы вместе. Всё это, конечно, касается начального школьного образования.

Wesha
11.03.2022 06:34+2К сожалению, проблема в том, что школьная программа заточена под середнячка.
А я в школе применял лайфхак: в начале урока, пока учитель объяснял материал, я минут за 10-15 прочитывал проходимый параграф учебника до конца, а оставшееся время урока решал прилагавшиеся в конце учебника домашние задания к этому параграфу, в результате чего домашнее время я мог посвятить другим вещам ;)

Wizard_of_light
11.03.2022 11:41+2О, да. Вот если бы в школе на тригонометрии на стене
такой плакат висел
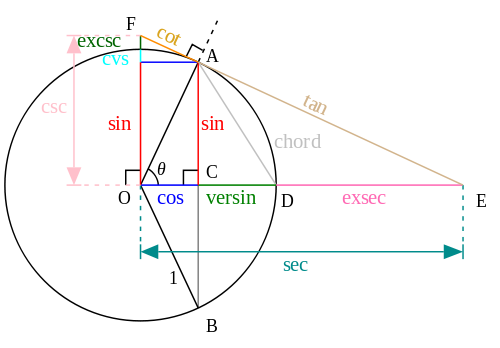
всё было бы понятнее.

piuzziconezz
11.03.2022 13:31Интересно, кто-нибудь применяет в практике что-то из этого, кроме sin, cos и tg?

Wizard_of_light
11.03.2022 14:09Ну, в кривошипно-шатунном механизме через версинус удобно смещение шатуна от фазы рабочего цикла выражать, если вдруг оно кому надо :) Секансы и косекансы в навигационных формулах применяют.

piuzziconezz
11.03.2022 15:16+2Я закончил университет по специальности инженер-системотехник, этих синусов там было - хоть жопой ешь, в работе часто с ними имею дело, а вот про существование версинусов узнал сегодня! Их даже на кнопках инженерных калькуляторов нету:)

mikleh
11.03.2022 20:53А это приводит нас к более фундаментальной дилемме: а) с одной стороны, людям, которые не собираются в дальнейшем изучать химию/биологию, такая детализация не нужна (хотя и безусловно полезна в формировании правильных основ дисциплины, без костылей и «забудьте все, чему вас учили в школе» в универе), с другой — вообще является полным бредом специализировать ученика в 7-8 классе.
Современная наука большая и сложная. Она просто не помещается в одну голову, времена универсальных ученых, таких как Ломоносов, давно ушли. В совершенстве можно знать какую-то область, но не все сразу. Поэтому задача школы именно сформировать общее правильное понимание. Пусть доказательства многих теорем останутся за рамками школьного курса, но не нужно пихать в детей искаженные факты. У нас даже те кто школу недавно закончили реально верят в ту же атомную модель Бора. В 2022 году-то. Да, современные модели сложные, но это ж не повод учить людей, про летающие шарики. Давно пора шарики заменить на облачка :)Вообще разделение физики и математики в школе, на начальном этапе изучения, мне кажется неправильным.
Хоть бы физику с химией объединили, я уж про математику молчу. Хотя по-хорошему да, физика — это продолжение математики начиная уже с 9 класса.К сожалению, проблема в том, что школьная программа заточена под середнячка.
Вот именно. Поэтому какой смысл в восхищаться тем, что вот мы «школьными» методами доказали то, что дается в школе. Такие доказательства сложны для понимания и интересны будущим математикам, но не середнячкам.О, да. Вот если бы в школе на тригонометрии на стене такой плакат висел всё было бы понятнее.
Нормальная шпаргалка. Школьнику, который в этом всем прямо сейчас варится, будет понятнее, чем стена текста. Только типографика конечно ужасная, на плакат не годится.
P.S. Извините, что в одном посте отвечаю, карма, три раза тьфу, мешает нормально писать.

sci_nov
10.03.2022 20:04+2Да, в школе про смысл дискриминанта как квадрата расстояния не дают. Прикольно у вас вышло.

AVI-crak
10.03.2022 22:41Вместо очечного способа решения уравнений, лучше-бы показали практический пример из реальности. Мне уже 47, но эти уравнения стабильно встречал исключительно в учебниках. Да, я знаю что на этих формулах половина геометрии и математики держится. Но это всё академические, нематериальное - в реальной жизни нафиг не нужное.
Ну и насчёт 100500 варианта решения школьной задачи. Отчего всяк и каждый хочет сделать это на бумаге карандашом. Может стоит написать один универсальный алгоритм, и отдать эту школьную задачу машинам (чтоб мучались вместо школяров).

ZetZet Автор
11.03.2022 00:10+2Это не новый способ решения уравнений. Это даже не исследовательская статья. Это исключительно компиляция и создание порядка в теме таким образом, чтобы это имело смысл, чтобы это было логично и вытекало одно из другого.
Текст не ставит своей целью рассказать о приложении квадратных уравнений. Такое ощущение, будто очень большая часть текста и информации в нем просто проигнорировано.
Основная суть всего текста — образование. А образование, это не всегда про приложение. В случае с такими предметами, как математика, это, скорее, про образ мышления: логичный, основанный на фактах, без рывков и скачков в логической цепочке. И чаще всего это — самое ценное, что может вынести из уроков математики тот, кто с ней связываться по жизни на профессиональном уровне больше не будет.
Такое чисто техническое видение темы образования удручает. Машины не будут мыслить за детей. Машине можно поставить задачу, решить то или иное уравнение, это факт. Но чтобы эту задачу банально сформулировать — нужно знать, о чем говоришь.

northzen
11.03.2022 04:59Ерунду какую-то написали.
Существует куча интересных задач, где вылазит поиск корней квадратного уравнения.
Какой смысл учить детей плавать, если они никогда ни бассейна, ни моря в глаза не видят?
Ki10V01T
11.03.2022 10:52+1Очевидно же: чтобы мыщцы и связки более развитые были.
А там они и мешки на складе поворочают более успешно и спину не надорвут. По зубам обидчику более крепко дадут и в целом, меньше проблем со здоровьем будет

northzen
11.03.2022 21:34+1Ничто не демотивирует детей больше, чем повторяемые мантры "надо мозг развивать".
Это роспись в педагогическом непрофессионализме. Можно отвечать "потому что я так сказал" и будет это и честнее, и понятнее.
Ki10V01T
11.03.2022 21:57Могу только отчасти с вами согласиться.
Одно верно точно: нужно делать систему образования более гибкой: подавать информацию более "предметно" и привязывать всю эту теорию к реальным вещам. Но все упускают момент работы с родителями. Многие проблемы детской неуспеваемости идут из сложных внутрисемейных конфликтов, из-за которых ребёнок вырастает дёрганным и неуверенным в себе. Дети вынуждены тратить силы не только на усвоение материала, но и на "войны" дома. А т.к. сил этих у детей не много - психика надламывается и включается защитный режим "я вообще ничего не хочу". Уходят годы, чтобы перетряхнуть голову, придти в себя, понять: "А что мне реально интересно? Чего я хочу?".Вот тут приходит осознание того, что сил на учёбу не было, множество прогалов в программе (что-то намеренно зубрили, что-то просто сливали). И даже в 20-25-30 лет в голове каша. И пытаешься снова "построить" эти логические цепочки размышлений, как они подразумевались школьным курсом. Проходить этот путь заново.
По поводу "мозг развивать". У нас в универе был один преподаватель дискретной математики. Очень позитивный дяденька. Ну так вот: он был после инсульта и его даже руки плоховато слушались. Но разум был чист и светел. (в свои 55+ он мог посоревноваться скоростью мысли с 20-ти-летними). Он очень любил математику и пытался её преподнести максимально просто и доступно. Видимо, она ему помогла восстановить когнитивные функции после столь тяжёлого удара. За то и благодарил свой предмет, популяризируя его.

Doberman341
11.03.2022 07:48Но это всё академические, нематериальное - в реальной жизни нафиг не нужное.
Сильное утверждение. То, что Вы явно не сталкивались с нахождением корней полиномов в реальной жизни, совершенно не означает, что не сталкивались совсем. Наверняка вы пользуетесь GPS-навигацией, а в приемнике как раз такие задачи и решаются.

Refridgerator
11.03.2022 08:02Не только GPS — любое устройство, связанное с передачей сигналов на расстояния, рассчитывается на полиномиальном мат.аппарате. Радио, Wi-Fi, NFC…

AVI-crak
11.03.2022 11:37Не только GPS
Со спутниковой навигацией работало 2,5 человека, все остальные получают готовые данные из модуля с закрытой прошивкой. С пеленгацией ещё печальнее, там подобный механизм упрятан в топологию аналоговой микросхемы. С наружи конечно всё цифровое, но корнями работал 1 человек, который микросхему проектировал.
Не надо приводить примеры, где эта задача уже решена. Нужна задача - где лично мне придётся вспоминать школьную математику.

terrapod
11.03.2022 12:04Давеча было на проде. Имеется список отелей, около 5 миллионов. По каждому есть координаты. Для каждого рассчитать, сколько отелей в радиусе 5/10/20 км. Решало его человек пять, методом проб и ошибок, все говорили, что математика - никому не нужна. Пара вообще не вдупляла, как. Пара сделала, но процесс работал несколько часов. Пятый, наконец то, справился.

Refridgerator
11.03.2022 12:08Ну откуда мне знать, чем лично вы занимаетесь. Даже в быту знания математики не повредят — количество рулонов для поклейки обоев рассчитать или 70% уксус до 15% разбавить. А в текущих реалиях вполне может возникнуть необходимость и свои GPS-приёмники на коленке собирать и программировать их самостоятельно.

AVI-crak
11.03.2022 18:51Ну откуда мне знать, чем лично вы занимаетесь.
Количество рулонов считается через целые числа, иначе второй раз в магазин придётся идти. Для процентов иная математика, со своими законами. А для спутников используется достаточно простая формула с линейным приближением. Потому-что невозможно на восмибитном мк выполнить точный расчёт одним махом, он захлебнётся на программной математике двойной точности.
По прежнему ищу реальную задачу, в которой необходимо решать квадратные уравнения. Не из учебника, а из реальности.

Refridgerator
11.03.2022 20:12Интерполяция сплайнами Безье тянет на реальную задачу? Чтобы найти с ними пересечение, придётся решать уравнения — квадратные, кубические и далее.

AVI-crak
12.03.2022 01:43Безье
Для рисования применяется линейный цикл с приближением. А вот для нахождения уникальной точки пересечения - тут я согласен, длинные муторные вычисления с большим выделением памяти. Просто сама задача точки пересечения считается академической - в реальности не используется вообще никогда. Гораздо быстрее решение находится приближением.
Даже в баллистике!!! Вместо длинных громоздких формул - компьютер быстро посчитывает кривую от начала до конца. Так проще и быстрее.
И да, у вояк до компьютеров были готовые таблицы, без всяких уравнений.

Doberman341
12.03.2022 07:41А для спутников используется достаточно простая формула с линейным приближением. Потому-что невозможно на восмибитном мк выполнить точный расчёт одним махом, он захлебнётся на программной математике двойной точности.
Вы говорите о способе вычислений, а не о сути - нахождении корней. Чтобы оптимизировать численный метод, понимание линейной алгебры необходимо. У Вас сама формулировка вопроса размыта. Мне, к примеру, не раз приходилось решать такие задачи (чаще как вспомогательные) при разработке разного железа. Что ж теперь, не считать мою жизнь реальной? Я не сторонник холивара на тему "Математика развивает воображение" и частично с Вами согласен - можно обойтись без всех этих формул. Но утверждать, что это не нужно "в реальной жизни" не стал бы...

maxx_s
11.03.2022 01:45Раз уж на то пошло, можно было в качестве бонуса или спойлера для следующей статьи рассказать об оптическом свойстве параболы.

Refridgerator
11.03.2022 12:15И не только оптическом. Параболическая антенна фокусирует отражённый радио-сигнал в одну точку, многократно увеличивая его мощность.

andersong
11.03.2022 14:00+1А гиперболический отражатель собирает отраженный свет в световой шнур, способный разрезать или расплавить все что угодно!©

piuzziconezz
11.03.2022 13:36Мне кажется, что в школьной программе вообще можно было бы обойтись без квадратных уравнений. По крайней мере, до 10 класса. Мне уже 45, всю жизнь работаю инженером-электронщиком, делал много расчетов прецизионной измерительной техники, писал софт, но решать квадратные уравнения пришлось пару-тройку раз за все время! Понимаю, в каких-то областях это, может быть, повседневная необходимость. Но в школе без специализации зачем это все?

Alexandroppolus
11.03.2022 14:28Мне кажется, что в школьной программе вообще можно было бы обойтись без квадратных уравнений
Смутно припоминаю, что в школьном курсе физики они выскакивают повсеместно в решении задач, ещё задолго до 10 класса.

piuzziconezz
11.03.2022 14:44Да, в решении задач с ускорениями возникают. Но до 10 класса можно, наверное, обойтись без этих задач. Например, пусть высчитывают путь по заданным начальной скорости, ускорению и времени, тогда решать уравнение не надо. Для понимания сути достаточно. С 10 класса можно заняться квадратными уравнениями, а то и в 11.

maxx_s
11.03.2022 17:25"Математику уже затем учить надо, что она ум в порядок приводит" @Ломоносов М. В.
И если не квадратные уравнения то что тогда? Способность ребёнка немного подумать взять параметры подставить в формулу и получить ответ, рождает в мозгу нужные нейронные связи. Потом во взрослой жизни этот человек сможет формуле посчитать кешбек, например, или процент по ипотеке.

Ivanzabu
11.03.2022 14:56Я выскажу наверное непопулярную точку зрения - но как человеку уже давно далекому от математики - мне объяснение теоремы виета в таком виде и всей статьи целиком в целом не чуть не показательнее чем при объяснении в школьном порядке. Возможно оно так и логичнее - но будь я ребенком ничего бы все равно не понял (да и сейчас понял только очень сильно напрягшись).
Вам (автору статьи) вероятно как человеку работающему с математикой куда чаще это кажется более очевидным и последовательным объяснением но не уверен что по факту это так.
ZetZet Автор
11.03.2022 16:12Резонное замечание.
Когда я писал статью, я старался создать повествование таким образом, чтобы ничто не принималось как факт без обоснования. Это и был мой критерий «логичности».
В то же время, я опирался на скромный опыт преподавания школьникам. Я примерно понимал, какими категориями они мыслят в той или иной задаче.
И самый последний источник «вдохновения» — те методы обучения, которые используют лучшие, по моему мнению, преподаватели моей альма-матер.
Естественно, это поймут не все, кому-то такой подход покажется чужеродным (даже люди в комментариях выше), но я хотя бы попытался показать альтернативу школьному подходу.

Fodin
11.03.2022 20:52Мне кажется, что если избавить статью от господствующего канцелярита - будет более лучшая статья. Не менее понятная, чем данная.

dbalabanov
13.03.2022 11:52очень интересно.
не понял смысл фраз "Вершина параболы да половину расстояния между корнями в обе стороны "




Alexandroppolus
Какой-то запутанный вывод корней и дискриминанта. Через упомянутое приведение к полному квадрату проще можно.
ZetZet Автор
Соглашусь с тем, что приведение к полному квадрату проще. Но суть то в том, чтобы показать привычные вещи таким образом, чтобы это имело какой-то смысл. В данном случае, геометрический.
Вывод корней таким способом ни чуть не сложнее, чем приведение к полному квадрату.
Alexandroppolus
Насчет расстояния интересный момент, не задумывался об этом.
Забавно, что даже при отрицательном дискриминанте, последний всё равно будет квадратом расстояния между корнями, только уже "по вертикали", то есть по мнимой оси.
Physmatik
Не сказал бы, что сильно проще, если честно. Вывод хоть и прямолинеен, но довольно длинный, особенно как для 7-8 классов. Кроме того, он слишком уж… механичен, что ли.
Приведённый в статье путь лучше, потому что связывает воедино разрозненные концепты, плюс во многом опирается на визуально-геометрическую интуицию, что для среднего школьника упрощает понимание. Для него ведь парабола и квадратное уравнение особо не связаны — преподают-то их отдельно.
Кстати, Грант Сандерсон [3blue1brown] в начале ковидной эпохи (как давно это было) записал для школьников примерно такое же видео https://www.youtube.com/watch?v=MHXO86wKeDY.
playermet
Еще сравнительно недавно было видео от Veritasium: https://www.youtube.com/watch?v=cUzklzVXJwo