Класс set (множество) — это одна из ключевых структур данных в Python. Она представляет собой неупорядоченную коллекцию уникальных элементов. Класс set, в некоторой степени, соответствует математическому множеству. Многие широко используемые математические операции, применимые к множествам, существуют и в Python. Часто вычисления, производимые над множествами, оказываются гораздо быстрее, чем альтернативные операции со списками. В результате, для того чтобы писать эффективный код, Python-программисту просто необходимо уметь пользоваться множествами. В этой статье я расскажу об особенностях работы с классом set в Python.

Инициализация множеств

Существует два способа создания объекта set: с использованием конструкции set(iterable) и путём помещения элементов, разделённых запятыми, в фигурные скобки — { ... }. Если же при инициализации множества попытаться воспользоваться пустыми фигурными скобками — {} — тогда будет создан словарь, а не пустое множество. Для создания пустых множеств используется команда set(). Обратите внимание на то, что при инициализации множеств порядок элементов неважен, и на то, что дублирующиеся элементы в множество добавить не получится.

a = { "a", "b", "c", "d", "e", "f", "f" }
# конструктору set можно передать любой итерируемый объект
b = set(["a", "b", "c", "d", "e", "f"])
c = set(("a", "b", "c", "d", "e", "e", "f", "f"))
# порядок элементов неважен
d = set(["d", "e", "f", "a", "b", "c"])
# деструктурирование списка
e = { *["a", "b", "c", "d", "e", "f"] }
assert a == b == c == d == e

# в одном множестве могут храниться значения разных типов
f = set(["a", True, 123])
g = { "a", True, 123, True, 123 }
assert f == g

# set() - это множество, а {} - это словарь
assert set() != {}

Какие элементы можно включить в состав множества? Это могут быть только элементы иммутабельных типов. Сюда входят такие типы, как float, int, string, bool и прочие подобные. А вот мутабельные типы — списки, словари, да и сами множества, в состав множеств включать нельзя. Если вас интересуют подробности о типах данных в Python — рекомендую почитать эту статью. Учитывая вышесказанное — следующая конструкция вызовет ошибку:

{ ["a", "b", "c"], True }
# => TypeError: unhashable type: 'list'

Но что если случается так, что в множествах надо хранить некие уникальные последовательности значений? Подробнее об этом мы поговорим в конце статьи.

Примечание об иммутабельности

Иммутабельность — это ограничение, касающееся лишь встроенных типов. На практике, чтобы объект можно было добавить в множество, или чтобы его можно было использовать в качестве ключа в словаре, этот объект всего лишь должен быть хешируемым. По умолчанию объекты пользовательских классов обладают хешем, основанным на их идентификаторах. Равенство объектов определяется по их идентификаторам. Это значит, что два объекта, идентичные в плане атрибутов, будут равны друг другу только тогда, когда они представляют один и тот же объект, или в том случае, если для них определён пользовательский оператор eq.

Если для некоего класса определён пользовательский оператор eq, то объекты этого класса перестают быть хешируемыми, если только для них не будет определён пользовательский оператор hash. Тут важно то, что если два объекта равны, то их хеши тоже должны быть равны. В противном случае при добавлении подобных объектов в словарь или в множество возникнут проблемы. Дело в том, что при проверке наличия значения в составе ключей словаря или в составе множества, проверяются и хеши и равенство объектов.

Единственный случай, когда в множестве имеет смысл хранить мутабельный объект, или когда такой объект может играть роль ключа словаря, это когда оператор проверки равенства объекта не использует его мутабельные атрибуты. Предположим, у некоего объекта имеется оператор равенства и соответствующая хеш-функция, основанные на атрибутах этого объекта. Если такой объект сначала добавить в множество, а потом поменять его, тогда хеш-значение, использованное при его сохранении, будет отличаться от текущего хеш-значения. Это — плохая практика.

Добавление элементов в множества

Существует множество способов добавления элементов в множество. Для того чтобы осуществить изменение (мутацию) множества, отдельный элемент в него можно добавить командой .add(). Итерируемый объект добавляют командой .update(), или, что то же самое, используя оператор |=:

a = set()
# добавление строкового элемента
a.add("hello")
# Следующий код НЕ эквивалентен предыдущему.
# Метод update ожидает поступления итерируемого объекта, поэтому
# строка рассматривается как итерируемый объект, содержащий символы
# которые и добавляются в множество
a.update("hello")
assert a == { 'hello', 'h', 'e', 'l', 'o' }
# А тут в множество добавляются две строки, так как они размещены в списке
a.update(["hi", "world"])
assert a == { 'hello', 'h', 'e', 'l', 'o', "hi", "world" }

Под «мутацией» я понимаю изменение исходного объекта. Есть ещё команды, которые не изменяют исходное множество. Например — метод .union(), или его эквивалент — оператор |:

a = { "a", "b" , "c" }
b = { "a", "c", "d" }

assert a | b == a.union(b) == { "a", "b", "c", "d" }
# исходные объекты не изменились
assert a == { "a", "b" , "c" } and b == { "a", "c", "d" }

Явное различие поведения методов .update() и .union() можно продемонстрировать, разобрав следующий пример:

def add_to_set1(a, b):
    a.update(b)
    return a

def add_to_set2(a, b):
    a = a.union(b)
    return a

a = { "a", "b" , "c" }
b = { "a", "c", "d" }

# Исходный объект был модифицирован
# и будет равен возвращённому объекту
assert a == add_to_set1(a, b)

a = { "a", "b" , "c" }
b = { "a", "c", "d" }

# Исходный объект НЕ был модифицирован
# и не будет равен возвращённому объекту
assert a != add_to_set2(a, b)

И наконец — два множества можно конкатенировать, использовав деструктурирование:

a = { "a", "b" , "c" }
b = { "a", "c", "d" }
assert { *a, *b } == { "a", "b", "c", "d" }

Этот приём будет работать аналогично методу .union(), но я рекомендую пользоваться именно .union().

Обратите внимание на то, что в предыдущих примерах я пользовался методом .update(), но в них можно было бы применить и оператор |=. Это значит, что a |= b ( .update() ) — это НЕ то же самое, что a = a | b (.union()). Дело в том, что в первом фрагменте кода осуществляется изменение объекта, хранящегося в a, а во втором примере a назначается новое значение.

Удаление элементов множеств

Мы рассмотрели команды для добавления элементов в множества. Существуют похожие на них команды, применяемые при удалении элементов. Вот как эти команды можно соотнести с уже известными вам командами:

• Аналог .add() — .remove().

• Аналог .update() — .difference_update() или -=.

• Аналог .union() — .difference() или -.

Рассмотрим примеры:

a = { "a", "b" , "c" }
a.remove("b")
assert a == { "a", "c" }

a = { "a", "b" , "c" } 
# Так же, как .update(), эта команда ожидает итерируемый объект
# В результате здесь удаляются "a" и "b",
# а не целая строка "ab"
a.difference_update("ab")
assert a == { "c" }

a = { "a", "b" , "c" } 
a.difference_update(["ab"])
# "ab" нет в составе элементов множества, поэтому ничего не удаляется
assert a == { "a", "b", "c" }

# Оператор -, эквивалент метода .difference(),
# не модифицирует исходный объект
a = { "a", "b" , "c" } 
b = a - { "b", "c" }
assert a != b and b == { "a" }

Снова хочу обратить ваше внимание на то, что надо помнить о разнице между конструкциями вида a -= b (исходное множество изменяется) и a = a — b (исходное множество не изменяется).

Имеется и ещё несколько методов, которые могут пригодиться для удаления объектов:

• .clear() — очищает множество.

• .remove() — удаляет элемент лишь в том случае, если он существует (в противном случае выдаёт ошибку); .discard() — работает похожим образом, но, если элемента не существует, ошибку не возвращает.

• .pop() — удалит случайный элемент из множества и вернёт этот элемент.

Другие операции для работы с множествами

Одна из сильных сторон Python-множеств заключается в наличии большого количества стандартных операций, предназначенных для работы с ними. Мы обсудили команды для модификации множеств путём добавления и удаления элементов, но это — далеко не всё, что можно делать с множествами.

Пересечение множеств

Пересечением двух множеств является множество элементов, входящих в состав обоих множеств. Для выполнения этой операции используются следующие методы и операторы:

• Команды, при выполнении которых множество не меняется: .intersection() или &. Например — a.intersection(b) или a & b.

• Команды, при выполнении которых множество меняется: .intersection_update() или &=.

Пример:

a = { "a", "b", "c" }
b = { "b", "c", "d" }
assert a & b == { "b", "c" }

Симметрическая разность множеств или дизъюнктивное объединение

Симметрическая разность множеств — это противоположность их пересечению. Она даёт все элементы, которые не принадлежат одновременно обоим исходным множествам. Для нахождения симметрической разности множеств используются следующие методы и операторы:

• Команды, при выполнении которых множество не меняется: .symmetric_difference() или ^. Например — a.symmmetric_difference(b) или a ^ b.

• Команды, при выполнении которых множество меняется: .symmetric_difference_update() или ^=.

Пример:

a = { "a", "b", "c" }
b = { "b", "c", "d" }
assert a ^ b == { "a", "d" }

Методы проверки наличия элементов в множествах, сравнение множеств

Я рассказал о том, как модифицировать множества, но они, в основном, используются для того, чтобы быстро проверять, имеются ли в них некие элементы, или нет. Подобные операции, выполняемые на списках, будут медленнее. Посмотрим на конструкции, используемые для проверки наличия элементов в множествах, и на некоторые другие полезные команды.

Проверка принадлежности элемента множеству

Вероятно, это — та операция, к которой вы будете прибегать чаще, чем к другим. Проверка наличия элемента в множестве выполняется с помощью оператора in. А проверка отсутствия элемента — с помощью оператора not in. Для таких операций над множествами, в отличие от подобных проверок, выполняемых в применении к спискам, характерна константная временная сложность — O(1). В результате, по мере роста размеров множества, не будет страдать скорость проверки наличия или отсутствия в нём неких элементов.

a = { "a", "b", "c" }
assert "a" in a
assert "d" not in a

Проверка того, является ли одно множество подмножеством другого

Множество является подмножеством другого множества в том случае, если все элементы первого множества входят в состав второго. Например, (A, B, C) — это подмножество (A, B, C, D). В Python подобную проверку можно провести, воспользовавшись методом .issubset() или оператором <=. Чтобы проверить, является ли одно множество истинным подмножеством другого, то есть — что одно множество — это подмножество другого, и что эти множества не равны, можно воспользоваться оператором <. Но учитывайте, что ещё можно пользоваться операторами >= и >.

a = { "a", "b", "c" }
b = { "a", "b" }
assert a.issubset(b) == (a <= b) == False
assert b.issubset(a) == (b <= a) == True
# Множество - это подмножество (но не истинное подмножество) самого себя
assert a.issubset(a) == (a <= a) and not a < a
# изменение направления
assert a >= b and a > b

Проверка того, что в двух множествах нет общих элементов

Если в множествах нет общих элементов, их называют непересекающимися множествами. В Python соответствующая проверка выполняется с помощью метода .isdisjoint().

a = { "a", "b", "c" }
b = { "a", "b" }
c = { "d" }
# без isdisjoint()
assert len(a & c) == 0 and len(a & b) != 0
# с этим методом
assert a.isdisjoint(c) and not a.isdisjoint(b)

Абстракция множеств

Так же, как и в случае со списками и словарями, при работе с множествами можно воспользоваться так называемой абстракцией множеств (set comprehension). Делается это путём добавления обрабатываемого выражения в фигурные скобки и через возврат единственного мутабельного элемента на каждом проходе цикла: { <element> for ... in ... }.

# преобразование списка в множество с добавлением 1 к каждому элементу
assert { i+1 for i in [1, 2, 3, 4] } == { 2, 3, 4, 5 }

# только чётные числа
a = { i for i in range(10) if i % 2 == 0 }
a.update({ -3, 100 })
# Преобразование множества в список с добавлением 1 к каждому элементу
# ВНИМАНИЕ: перебирая множество, не рассчитывайте на то, что сохранится тот
# порядок следования элементов, в котором они были в него добавлены
print([i+1 for i in a])
# => [1, 3, 5, 101, 7, 9, -2]

Хранение в множествах данных более сложных типов

Представьте, что у нас имеется цикл, на каждой итерации которого мы обходим некоторое количество узлов графа. Предположим, мы обошли граф два раза, у нас получились следующие пути:

A -> B -> D
D -> C -> E -> B

Потом надо быстро проверить, прошлись ли мы по определённому пути. Нужно, чтобы такая проверка проводилась бы быстро, поэтому совершенно естественным будет использовать для её реализации множество. Как это сделать, если список, из-за его мутабельности, нельзя добавить в множество? К нашему счастью, в подобных обстоятельствах можно воспользоваться кортежем, классом tuple, который, по сути, представляет собой иммутабельную версию списка. Рассмотрим пример.

Сначала создадим граф, используя словарь. Ключи словаря будут представлять узлы графа, а значения — списки узлов, в которые можно перейти из текущего узла.

# можно перейти от ключа к значениям
graph = {
    "A": ["B", "D", "F"],
    "B": ["C", "F"],
    "C": ["D", "E"],
    "D": "A",
    "E": "F",
    "F": "B",
}

Визуализировав это описание, я получил такой граф.

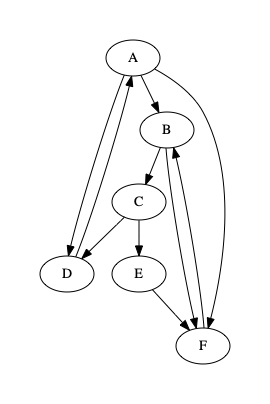
Если вы задаётесь вопросом о том, как я создал такой граф — знайте, что сделал я это, прибегнув к graphviz и написав следующий код:

from graphviz import Digraph

dot = Digraph()
for k in graph.keys():
    dot.node(k, k)
edges = []
for k, v in graph.items():
    edges += [f"{k}{to}" for to in v]
dot.edges(edges)
dot.render(view=True)

Теперь я займусь случайным блужданием по графу, проходя от 1 до 10 узлов, после чего сохраню результирующие пути в объекте set в виде кортежей. Посмотрим, сколько уникальных путей мы сможем сгенерировать за 100 проходов по графу:

import random

def perform_random_walk(graph, n_steps):
    node = random.sample(list(graph), 1)[0]
    path = [node]
    for _ in range(n_steps):
        node = random.sample(graph[node], 1)[0]
        path.append(node)
    return tuple(path)
    
paths = set()
lengths = list(range(1, 10+1))
for _ in range(100):
    paths.add(perform_random_walk(graph, random.choice(lengths)))
len(paths)
# => 83

Из 100 случайных проходов по графу 83 оказались уникальными.

А что если нас не волнует порядок узлов, а нужно лишь сохранить сведения о посещённых узлах? Тогда будет смысл хранить отдельные пути в множествах, но, как уже было сказано, множества мутабельны, помещать их в другие множества нельзя. В такой ситуации, вместо обычных множеств, описываемых классом set, можно прибегнуть к неизменяемым множествам, представленным классом frozenset. Чтобы это сделать — поработаем с кодом цикла из предыдущего примера:

paths = set()
lengths = list(range(1, 10+1))
for _ in range(100):
    path = perform_random_walk(graph, random.choice(lengths))
    paths.add(frozenset(path))
len(paths)
# => 21

Итоги

Множества — это полезный инструмент Python-разработчика. Они позволяют очень быстро выполнять определённые операции, что способно значительно повысить эффективность кода. Кроме того, в Python имеется немало простых и полезных методов для работы с множествами, применение которых способствует упрощению кода.