
Пропорция золотого сечения известна людям уже несколько тысяч лет и всё это время не теряет популярности как в чисто математической среде, так и среди художников, скульпторов, философов, биологов. Золотое сечение можно найти в:
Классической живописи
Скульптуре
Архитектуре
Принципах перспективы и композиции фотографий
Пропорциях человеческого тела
Ракушках
Растениях
Развитии эмбрионов
Ветвях галактик
И во множестве других, подчас весьма необычных, сфер.
Сегодня мы будем говорить о растениях.
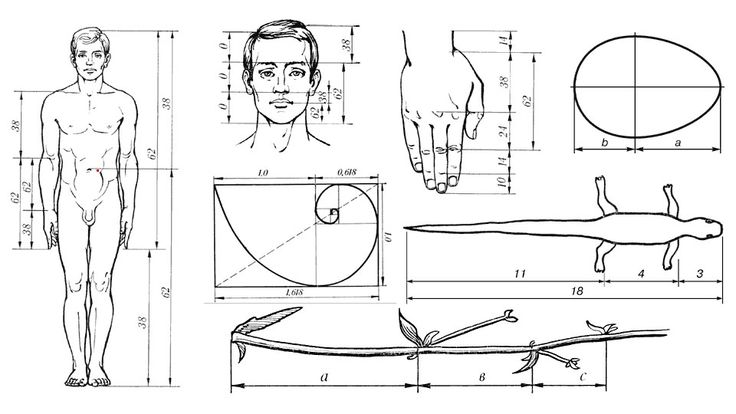
Идея золотого сечения очень проста. Возьмем отрезок, и разделим его на две части Существует единственный способ разделить отрезок на две части с длинами ,
так что отношение длины всего отрезка к большей части равно отношению большей части к меньшей. В самом деле, пусть длина отрезка
; по условию
Определив и немного преобразовав систему, получим квадратное уравнение:
У этого уравнения единственный положительный корень
Число называется числом Фидия или, попросту, пропорцией золотого сечения.
На заглавной картинке изображен цветок подсолнечника маслянистого - растения, масло из семян которого вы почти наверняка регулярно употребляете в пищу. С точки зрения ботаники, большой красивый цветок подсолнуха называется "соцветием-корзинкой". Желтые лепестки соцветия - видоизмененные листья; они окаймляют корзинку из крошечных желтых цветков, каждому из которых после опыления суждено превратиться в семечко. Рассматривая корзинку подсолнуха, мы можем обнаружить удивительный факт:

Человеческий глаз легко различает, как семена группируются по спиралям - левым и правым. Их число различно. Приложив усилия, можно сосчитать, что в цветке подсолнуха на фотографии 21 спираль идет по часовой стрелке и 34 спирали - против часовой. Количества подобных спиралей называются в ботанике парастическими числами (parastichy numbers). Интересно то, что что близко к
. Это не случайно.

Оказывается, у множества видов растений у здорового, неповрежденного цветка или розетки имеется тенденция к выбору в качестве парастических чисел двух соседних чисел следующего ряда:
Эта последовательность широко известна как последовательность Фибоначчи. Она начинается с двух единиц; каждое следующее число последовательности - сумма двух предшествующих. У ряда Фибоначчи много замечательных свойств, главным из которых для нас является то, что отношение двух соседних членов стремится к . Этот замечательный факт напрямую вытекает из явной формулы для чисел ряда Фибоначчи, так называемой формулы Бине:
Как можно видеть, отношение двух соседних членов ряда Фибоначчи быстро стремится в . На самом деле, это характерно для любого рекуррентного ряда, строящегося по формуле "каждый следующий член равен сумме двух предыдущих".
Откуда же члены последовательности Фибоначчи взялись в цветке?
Процесс формирования корзинки называется филлотаксисом. Внутри центральной части корзинки подсолнуха - меристемы - происходит деление зародышевых клеток, образующих сначала цветок, а потом и семечко. Сразу после рождения цветок начинает выталкиваться младшими братьями и сестрами в радиальном направлении от центра.
Закон движения единичного цветка в корзинке проще всего описать в радиальной системе координат - по радиусу и углу. Для цветка номер из
рожденных меристемой, его радиальные координаты описываются примерно так:
Помимо и
мы видим здесь два параметра -
и
.
- некая постоянная величина, связанная с размерами цветка в соцветии.
Закон радиального выталкивания легко обосновать физически, приняв за внимание, что цветки соцветия приблизительно одинакового размера и должны покрывать собой всю свободную площадь корзинки. Интереснее закон направления
. Он зависит от константы
, которая для подсолнуха с высокой точностью равна
Иными словами, порождая цветок, меристема задает ему направление движения, каждый раз меняя его это направление относительно предшествующего поворотом на .

Это число, , неявным образом закодировано в геноме растения. Для того, что бы понять, что это и откуда оно берется, разделим его на
, то есть вычислим, какую долю полного оборота оно составляет:
Вот где прячется золотое сечение! Но зачем оно нужно растению?
Для ответа на этот вопрос, обратимся к уникальному свойству числа- его разложению в цепную дробь.
Любое действительное число можно представить следующим способом:
Где целое число; прочие
натуральные числа. Такое представление называется цепной дробью. Если число - рациональное, его представление в виде цепной дроби насчитывает конечное число членов, и вычисляется посредством алгоритма Евклида. В противном случае, представление числа в виде цепной дроби выражается бесконечной последовательностью знаменателей. Например, знаменитое число
расписывается в виде цепной дроби вот так:

Наиболее важным свойством цепных дробей для математики является то, что они кодируют наилучшие рациональные приближения данного числа. В самом деле, попробуем "обрезать" дробь по одной из контурных линий. Мы получим рациональное число, приблизительно равное . Утверждается, что для каждого из них не существует рационального числа с меньшим знаменателем, более близкого к
:
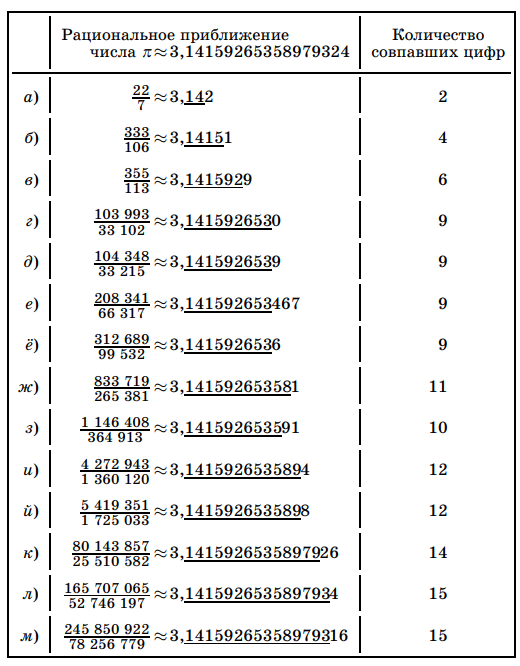
Сравните приближение и
И в том и в другом случае мы получили 6 значимых цифр после запятой, но в одном случае знаменатель - 113, а в другом - 10000000. Разница, как говорится, налицо.
Теперь, наконец, разложим в цепную дробь. Получится следующее:
Рациональные приближения, полученные посредством обрезания этого представления, выглядят так:
Легко видеть, что это ни что иное, как отношения соседних членов ряда Фибоначчи. И вот теперь, сравнивая цепочку рациональных приближений числа с аналогичной цепочкой числа
мы можем видеть главное математическое свойство пропорции золотого сечения.
Для любого достаточно большого , у
больше рациональных приближений со знаменателем меньше чем
, чем у любого другого иррационального числа.
В самом деле. Приближая , мы видим, что уже у седьмого приближения знаменатель вырос до 99532. У
знаменатель седьмой дроби - 34. Алгоритм вычисления рационального приближения из частичного представления цепной дроби прост, и мы не будем его здесь приводить. Выведя его, легко видеть, что чем меньше числа в ряду, тем меньше будут представления, а натуральных чисел меньше, чем ряд из последовательных единиц, нельзя и представить. Одновременно с этим,
является наиболее плохо приближенным числом из всех, в том смысле, что с ростом знаменателя число угаданных знаков приближения растет максимально медленно, насколько это возможно. Этот факт является прямым следствием из теоремы Гурвинца и его доказательство довольно занудно, так что мы не будем включать его в данную статью.
Суха теория, друзья, но древо жизни пышно зеленеет. Настало время сложить всё вышесказанное, и понять, как связаны: филлотаксис подсолнуха, угол , последовательность Фибоначчи, цепные дроби и рациональные приближения. И вместо того, что бы рассказать, лучше показать:
Интерактивное онлайн-демо, иллюстрирующее процесс филлотаксиса
Перейдя по ссылке, вы увидите небольшую онлайн-демонстрацию процесса формирования корзинки подсолнуха. Вы можете регулировать угол порождения меристемой цветков и их количество, или изучать спирали, полученные путем выделения каждого ного зерна, начиная с первого, где n (ранг) - знаменатель одно из рациональных приближений для выставленного вами угла. Вы увидите, что при углах
и некоторых других зерна в корзинке распределены почти равномерно, а число рациональных приближений с небольшим основанием максимально; для других углов число рациональных приближений невелико, а зерна подсолнуха четко группируются в спирали, причем их число соответствует знаменателю дроби того или иного рационального приближения выставленного угла. И глядя на это, даже не оперируя сложной математикой вы можете дать правильный ответ на поставленный в заголовке вопрос:
Золотое сечение в подсолнухе обеспечивает наиболее равномерное распределение семян в корзинке за счет наихудшего его приближения рациональными числами и максимизации числа спиралей небольшого ранга, вдоль которых упорядочены семена.
Настоящая статья написана по мотивам кружковых занятий Малого Мехмата МГУ для старших классов. В статье использованы следующие источники:
А. Цезинг "Эстетические исследования"
В. Арнольд "Цепные дроби"
А. Щетников "Загадки филлотаксиса" (видео)
"Математическая составляющая / Филлотаксис" - энциклопедия по популярной математике
"Special Topics - Lessons from Biology for Engineering Tiny Devices / Lessons 12: Spirals and phyllotaxis" - цикл популярных лекций Принстонского университета, посвященных спиралям.
Takuya Okabe, Atsushi Ishida and Jin Yoshimura - The unified rule of phyllotaxis explaining both spiral and non-spiral arrangements - более строгое математическое описание процесса развития цветка.
Математика листьев: как один необычный куст изменил уравнение модели роста растений - статья на habr.com с прелестными анимироваными иллюстрациями.
Wikipedia: Golden ratio, Continued fraction, Fibonacci number, Hurwitz's theorem.
Интерактивное онлайн-демо, иллюстрирующее процесс филлотаксиса
Комментарии (21)

ramil_trinion
19.10.2022 17:39+3Идея золото сечения настолько красива, что стала очень популярной ещё сотни лет назад и остаётся такой до сих пор. За это время она обросла мифами, а люди попытались найти заветное золотое соотношение даже там, где его нет.
Источник: https://un-sci.com/ru/2019/10/26/mify-o-zolotom-sechenii/

celen Автор
20.10.2022 12:45Замечательность приведенного в статье примера в том, что именно там золотое сечение гарантированно есть, и легко обосновывается биологической целесообразностью.

m03r
19.10.2022 21:13+2Интерактивное демо просто восхитительное! — сразу всё становится понятно. И ещё вспомнилось видео про спирали из простых чисел, не оно ли послужило источником вдохновения?

celen Автор
20.10.2022 12:43+1Сюжет 3Blue1Brown не относится к теме напрямую, но пересекается по части вопроса связи распределения частиц в спирали с рациональным приближением числа. Главное отличие - у них используются Архимедовы спирали с постоянным шагом, а для виртуального подсолнуха использовалась спираль Ферма

iShrimp
20.10.2022 19:25Интересно, что визуально воспринимаемое количество спиралей зависит от масштаба. По мере уменьшения масштаба спирали становятся более пологими и незаметными, а вместо них становятся видны крутые спирали более высокого порядка. У подсолнуха спиралей больше не потому, что "золотое сечение" другое, а просто из-за масштаба.

m03r
21.10.2022 11:09Да, согласен, просто хотелось отметить, что Ваша интерактивная визуализация обладает такой же «магией наглядности», превращающей не самые простые выкладки в нечто совершенно очевидное.

VDG
20.10.2022 01:24Не про подсолнухи, а про людей/животных.
Лефевр В. А., Что такое одушевлённость?
2.3. Феномен золотого сечения при выборе и категоризации
стр. 31
… Он (феномен золотого сечения) появляется тогда, когда у испытуемых нет операциональных возможностей для выделения в стимуле качества, по которому требуется произвести оценку.
Формулы и эксперименты тоже там приведены.
celen Автор
20.10.2022 12:48+2Спасибо, весьма интересный материал.
Фактически, у Лефевра показано на примере нескольких психологических экспериментов, что люди имеют склонность при любой категоризации каких-то сущностей на "хорошее" и "плохое", разделять их так, что доля "хорошего" оказывается приблизительно в (Ф-1) = 0.62 от целого, а доля плохого - в (2-Ф) = 0.38 , а эти два числа в отношении между собой образуют золотое сечение.
Проблема этого рассуждения, как мне показалась, в том, что психологические эксперименты очень неточны и с тем же успехом это может быть разделение на 2/3 и 1/3, например. Попытка же как-то математически обосновать феномен кажется мне, как не-психологу, сомнительной.
NumLock
20.10.2022 02:45Золотое сечение в подсолнухе обеспечивает наиболее равномерное распределение семян в корзинке за счет наихудшего его приближения рациональными числами и максимизации числа спиралей небольшого ранга, вдоль которых упорядочены семена.
Кому/чему оно это обеспечивает? Какой в этом смысл для жизни растения?
42?

Politura
20.10.2022 06:38+3Какой в этом смысл для жизни растения?
Ну очевидно же: более равномерное распределение -> меньше площадь -> выше эффективность, а значит и выживаемость, менее эффективные, которым для достижения такого-же результата надо больше ресурсов проиграли в эволюционной гонке.
NumLock
20.10.2022 14:56Ну очевидно же: более равномерное распределение -> меньше площадь -> выше эффективность
Эффективность чего?
для достижения такого-же результата надо больше ресурсов проиграли в эволюционной гонке
Какого результата? Почему бы растению в эволюционном процессе не увеличить возможность получения больше ресурсов чем быть более компактным?
----
Возможно вектор эволюционного процесса создавался не самим растением, а насекомыми опыляющие его. У насекомых есть глаза. И им куда более привлекательны цветки более красивые (более пропорциональные) чем некрасивые (менее пропорциональные). Другими словами красивые цветы имеют больше шансов на воспроизводство.

celen Автор
20.10.2022 16:14+3Вы всё усложняете. Вот представьте - вы подсолнух. У вас есть эволюционная задача вырастить много семок, которые будут клевать птицы; идея в том, что часть семок в птичьих желудках не переварится и вместе с пометом упадет куда-нибудь в почву, где взойдет новый подсолнух. А до того, как попасть в птичий желудок, семка должна быть сформирована из опыленного цветка; опылять его будут летающие насекомые. В растительном мире есть полно самых разных способов решения этой задачи, но вы, как растение, пришли в результате эволюционного отбора к такому варианту:
Вы выращиваете один-единственный цветок гигантских размеров. Вы делаете его высоким, сколь это возможно для многолетней травы, ярко-желтым и вкусно пахнущим для приманивания пчел. Он возвышается над полем как рекламный баннер над дорогой и все пчелы в округе прилетают к вам. Пчела, в общем-то, видит вас как большое желтое пятно, видимое в траве с расстояния в сотни метров.
Теперь эволюционный отбор фиксирует для вас оптимальный размер семечки. Если она будет очень маленькой, птица переварит её целиком, а если очень большой - или птица не сможет заглотнуть семечку, и будет пытаться расколоть её, к тому же у вас так получится меньше семян из того же объема биомассы. И ещё - семечка должна быть круглой, а биомеханический способ, которым вы проращиваете зародыши цветков в соцветии, подразумевает, что вы формируете их по одному по спирали из центра к краю. Всё вышесказанное - вводные данные; а теперь главный вопрос - как вам правильно запрограммировать процесс развития побега, что бы у вас всё получилось?
Вам повезло - раз уж вы подсолнечник, всё придумано до вас. Растения изобрели золотое сечение ещё до того, как изобрели цветы, а в вашем роду Астровых этим знанием пользуются все ваши родственники, как ближние, так и дальние. Фактически вам нужно всего лишь установить на физический максимум параметр размера, подобрать состав олеиновой и линолевой кислоты в семках под воробьиные вкусы, а эфирных масел - под пчелиные, да покрасить листья в желтый поярче. Поднастройка параметров размера и химического состава - самая простая операция эволюционного процесса. Но есть один параметр, который вы не трогаете - это настройка угла поворота в центрах концентрации гормона клеточного деления в меристеме в 135.5 градусов. Малейшая, в десятую долю градуса, мутация в этом месте - и ваше единственное драгоценное соцветие получатся не плоским, перекошенным, с неровно разбросанными семенами, половина из которых не разовьется вообще - это если цветок-мутант вообще сможет раскрыться.
Позже на ваше поле приходит местный суперхищник Хомо, большой любитель ярких цветов и подсолнечного масла, который встраивает вас в свою экосистему, делая ваш цветок ещё больше, а ваши семечки - ещё жирнее, насколько это вообще возможно. Но это уже совсем другая история.
NumLock
21.10.2022 02:57Вот представьте - вы подсолнух. У вас есть эволюционная задача вырастить много семок,
Ох уж этот эгоцентризм :) У любого живого существа на земле нет эволюционной задачи. Есть определённые этапы развития из которых появляются определённые потребности. Которые оно удовлетворяет найденным им оптимальным на данный момент способом. В том числе к этому относятся и мутации. Эволюционный отбор совершается под внешним воздействием на живой организм. Будь то изменение в среде обитания, конкурентные сородичи или другие живые организмы.
Растения изобрели золотое сечение ещё до того, как изобрели цветы
Не льстите растениям. Они ничего не изобретают. Они даже не мыслят в рамках человеческого сознания. Растения выглядят так как отобраны в многолетних естественных выборках. За них это сделала биосфера, в которые входит большой комплекс живых организмов.

Azya
21.10.2022 10:44Вы придираетесь к формулировкам, хотя ясно, что автор использует эти обороты для упрощения изложения мысли. Такие обороты используются в любой популярной литературе, где затрагиваются вопросы эволюции (обычно авторы делают оговорку, что их не стоит воспринимать буквально).

excoder
21.10.2022 20:58+1Вот ещё в тему из недавнего: https://gizmodo.com/physicists-got-a-quantum-computer-to-work-by-blasting-i-1849328463.


excoder
Хотелось бы обосновать математически понятие "равномерности" и показать, как там возникает золотое сечение.
georgevp
http://www.delphis.ru/journal/article/pifagoriiskaya-programma-kak-sintez-idei-o-strukturnoi-tselostnosti-prirody
рекомендую ознакомиться.
Также, Жирмунский А.В., Кузьмин В.И. Критические уровни в процессах развития биологических систем. М.: Наука, 1982.
celen Автор
Помимо приведенного "The unified rule of phyllotaxis explaining both spiral and non-spiral arrangements", рекомендую "Анализ модели филлотаксиса" Б. Розина. http://www.trinitas.ru/rus/doc/0232/013a/2101-rzn.pdf , в которой дается более строгая математизация феномена. Я счел математику в обеих этих статьях слишком тяжелой для популярной лекции и не стал включать её в текст.
iShrimp
Если рассмотреть ряд a[i+1] = frac(a[i] + f) при разных f, то окажется, что при f = 0.618... значения ряда наиболее равномерно распределены в интервале [0; 1), т.е. периодические паттерны становятся минимально выраженными (а это обусловлено наихудшей рациональной приближаемостью числа Фи), и поэтому ряд золотого сечения используют для одномерного дизеринга. Природа выработала простой рекурсивный механизм, распределяющий цветки максимально равномерно, без скоплений и пустот.